CUDA学习笔记4

1.线程块的分解
2.多线程块&多线程下核函数的调用
3.线程进阶
4.其它知识点
- 针对图像的二维线程块
- 线程索引与像素

对应《GPU高性能编程CUDA实战中文版》第5章笔记

1.线程块的分解

在调用核函数时，我们可以通过指定尖括号中的数值来对线程块进行分解。之前也说过，尖括号中的第一个参数表示要启动的线程块的数量，硬件限制为65535。其实这是指对于一个线程格而言，每一维大小不能超过65535，不是总数不能超65535。若是一个二维线程格，那么最多可以有65535 × 65535个线程块。第二个参数表示每个线程块包含的线程数量，硬件限制为512。每个机器可能有所不同，可以通过maxThreadsPerBlock属性查询。如<<<2,100>>>则表示开启2个线程块，每个线程块包含100个线程，共有200个线程。总线程与线程块的关系可用以下公式表示：

N个线程块 × a个线程/线程块 = aN个线程

与获取线程块索引类似，对于每个线程而言，依然可以通过threadIdx获取索引。需要注意的是它获取到的是在包含它的block中的索引，而不是我们需要计算的全局索引。我们还可以通过blockDim来获取线程块某一维的大小。注意是某一维而不是block包含的全部线程数。对于一维线程块，blockDim.x获取到的就是该线程块中所有线程的个数。但对于二维则不是，获取到的则是x方向上的线程数。若要获取全部，应是x × y。同理我们可以通过gridDim来获取线程格的维数。需要注意的是gridDim是二维的，而blockDim是三维的。也就是说，CUDA允许启动一个二维线程格，并且每个线程格包含的每个线程块都是三维线程数组。对于多个线程块、多个线程的问题，是我们需要研究的重点问题。如何利用线程块和线程准确地获取某个线程唯一的索引是我们关心的。我们假设共有4个一维的线程块，每个线程块有5个线程。把线程块索引做行号，线程索引做列号。那么可以画出示意图如下所示：
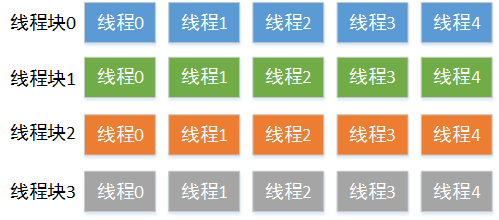这是一个将二维索引(x,y)变成一维索引i的问题。我们可以这样来计算各线程唯一索引：

int tid = threaIdx.x + blockIdx.x × blockDim.x

首先，我们获取到每一个block共包含多少线程(这里因为是一维block，索引只有x。若是二维，则应为 blockDim.x × blockDim.y来计算共包含多少线程)。然后获取到我们需要计算的线程所在的block的索引号，将索引号乘以每个block包含的线程数，在当前线程所在的block之前的所有线程数。然后再将这个值与当前线程块中的线程索引相加，即可得到最终的全局索引。
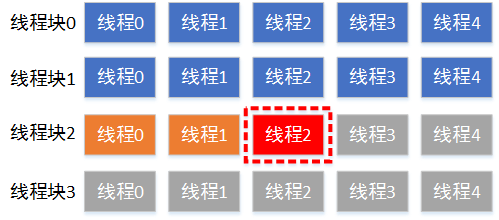如图所示，共有4个线程块(索引0 - 3)，每个线程块包含5个线程(索引0 - 4)，共20个线程。现在需要计算线程块2中线程2的全局索引。首先我们可以获取到每一个线程块的大小为5，然后获取到当前线程所在的线程块索引为2，也即在它前面有两个完整的线程块，所以共有2 × 5=10个线程，图中蓝色部分。然后该线程在当前block中的线程索引获取到为2，图中橙色部分。因此将两部分相加，即可得到全局索引为12。

2.多线程块&多线程下核函数的调用

假设我们共需要启动N个线程，每个线程块包含128个线程，那么根据之前的公式，需要启动N/128个线程块。当N为128的整数倍时，可以获得正确的计算结果。如N=256时，需要启动的线程块就是256/128=2个。但问题是，这是个整数除法。一旦N不是128的整数倍就会出现问题。例如当N=127时，计算结果是0，则会启动0个线程块，什么都不会执行。当N=150时，会启动1个线程块，那么这样就会有150-128=22个线程没有启动。对于这个问题，可以利用向上取整的办法解决。可以利用这个公式计算线程块个数：

B = (N+127)/128

当N=50，B=1；N=128，B=1；N=150，B=2。
这里还有个需要注意的地方，那就是比如需要启动的总线程数为150，但是启动了两个线程，也就是一共启动了256个线程。多启动了256-150=106个线程。这些多启动的线程怎么办呢？又会发生什么呢？
事实上，我们在核函数中其实已经解决了这个问题。关键在于if语句if(tid < N)。N为我们需要启动的总线程个数。可以很容易看出，如果tid大于等于N了，核函数会自动停止计算，什么都不会发生。核函数不会对越过数组边界的内存进行读取或写入。

3.线程进阶

之前我们一直都是有多少数据建立多少线程，一个线程只计算了一次。但其实是不现实的。如一幅影像有1300万像素，不可能同时建立1300万个线程处理。这就需要对有限数量线程的重复利用，让线程有序地重复计算完成工作。要解决这个问题，我们可以效仿一开始多核CPU的代码，将if(tid < N)换成while(tid < N)，完整代码如下：

__global__ void add(int *a,int *b,int *c)
{
  int tid = threadIdx.x + blockIdx.x * blockDim.x;
  while(tid < N)
  {
    c[tid] = a[tid] + b[tid];
    tid +=blockDim.x * gridDim.x;
  }
}

在这里使用while循环对数据进行迭代。在多CPU或多核版本中，每次递增的数量不是1，而是CPU数量。在GPU实现中，我们将并行线程的数量看成是处理器的数量。这样我们只需要解决计算每个并行线程的初始索引以及确定递增的量值这两个问题即可。
对于线程的初始索引，我们完全可以按照之前计算全局索引的办法。

int tid = threaIdx.x + blockIdx.x × blockDim.x

而确定递增量的问题。其实递增的步长就应该是线程格中正在运行的线程数量。这个值等于每个线程块中的线程数量乘以线程格中线程块的、数量，即blockDim.x × gridDim.x。这和多核CPU的递增思路是相同的，之前说了，这里我们把每个线程看成是一个处理器。

4.其它知识点

针对图像的二维线程块

如果某图像有DIM × DIM个像素，我们设定每个线程块中包含一个大小为16 × 16的线程数组。那么一共需要启动DIM/16 × DIM/16个线程块，从而使每个像素对应一个线程。假设我们某幅图像是1920*1080像素，如果按照这个算法，共要启动(1920/16) × (1080/16)=8040个线程块，也就是8040 × 16 × 16=2058240个线程。这在CPU中是难以想象的，同时启动200多万个线程用于数据处理，但是在GPU中便可以做到。下图是一个48 × 32像素的图片的线程块与线程配置情况。

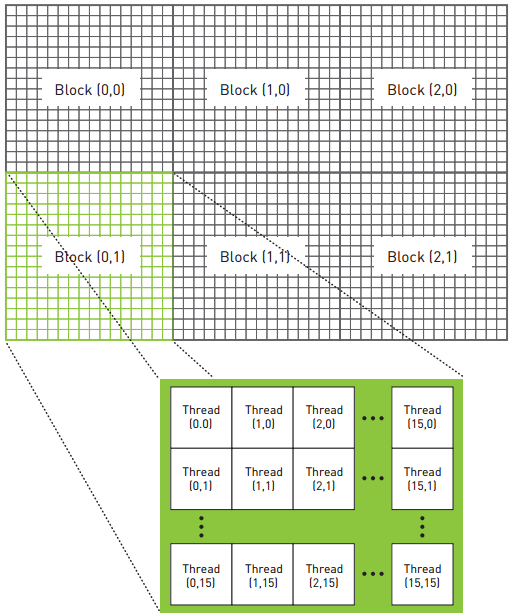
线程索引与像素

由于我们建立了那么多的线程，因此需要将线程与像素对应起来。核心代码如下：

int x = threadIdx.x + blockIdx.x * blockDim.x;
int y = threadIdx.y + blockIdy.y * blockDim.y;
int offset = x + y * blockDim.x * gridDim.x;

在代码中，首先每个线程都得到了它在线程块中的索引以及这个线程块在线程格中的索引，并将这两个值转换为图形中的唯一索引(x,y)。例如位于线程格中(12,8)处的线程块中的(3,5)处的线程开始执行时，它知道在其左边有12个线程块，上边有8个线程块。在这个线程块内，左边有3个线程，上边有5个线程。需要注意的是线程的索引是从0 开始的，而且横向的是x，纵向的是y。由于每个线程块都有16个线程，这就意味着这个线程有：

3线程+12线程块 × 16线程/线程块=195个线程在其左边

5线程+8线程块 × 16线程/线程块=133个线程在其上边

而这个计算求得的便是x、y值，也就是将线程和线程块索引映射到图像坐标的算法。到这一步后，我们还需要用到之前说过的线性化索引的方法，将二维的x、y索引转变成一维的索引。

int offset = x + y * blockDim.X * gridDim.x；

我们首先要获取每一个线程块x维包含的线程个数，然后获取线程格 x维包含的线程块个数。这样便能计算出整个线程格中x维包含的总的线程个数。将这个数值再乘以当前线程在y方向上的索引y，即可求得所有在其上面的线程数量。最后再加上当前x方向中的x索引，即可算出唯一的索引值。其实可以发现，如果采用y方向来计算，同样可以得到唯一的索引值。

int offset = y + x * blockDim.y * gridDim.y;

Menu