对应《机器学习实战中文版》第14章笔记
矩阵分解
在多数情况下,数据中的一小段携带了数据集中的大部分信息,其它信息要么是噪声,
要么是毫不相关的信息。矩阵分解可以将原始矩阵表示成新的易于处理的形式,
这种新形式是两个或多个矩阵的乘积。这类似于因数分解,如12分解成两个数相乘,
1×12、2×6、3×4都是合理的答案。
矩阵分解有很多技术,其中一种便是SVD,英文全称Singular Value Decomposition,中文
名称奇异值分解。SVD将原始数据集矩阵Data分解成三个矩阵U、Σ和V^T。如下公式表示:
上述分解中会构建出一个矩阵Σ,该矩阵只有对角元素,其它元素均为0,且对角元素是从大到小排列的。
这些对角元素称为奇异值(Singular Value),它们对应了原始数据矩阵Data的奇异值。
奇异值是与特征值有关的。它就是矩阵Data*Data^T的特征值的平方根。
前面说到Σ只有从大到小排列的对角元素。在科学和工程中,一直存在这样一个普遍事实:
在某个奇异值的数目(r个)之后,其它的奇异值都置为0。也就意味着数据集中仅有r个重要特征,
而其余特征则都是噪声或冗余特征。
利用Python实现SVD
简单的例子
例如有如下矩阵:
\[\begin{bmatrix} 1 & 1\\ 7 & 7 \end{bmatrix}\]对其进行SVD分解,这里需要引用numpy。代码如下:
from numpy import *
U, Sigma, VT = linalg.svd([[1, 1], [7, 7]])
print "U:\n" + U.__str__()
print "Sigma:\n" + Sigma.__str__()
print "VT:\n" + VT.__str__()
输出结果如下:
U:
[[-0.14142136 -0.98994949]
[-0.98994949 0.14142136]]
Sigma:
[ 10. 0.]
VT:
[[-0.70710678 -0.70710678]
[-0.70710678 0.70710678]]
需要注意的是,这里Σ是以行向量的形式返回的,而非如下矩阵:
\[\begin{bmatrix} 10 & 0\\ 0 & 0 \end{bmatrix}\]产生这种情况的原因是,由于矩阵除了对角元素其它均为0,因此这种仅返回对角线元素的方式可以节省空间。 而我们需要记住的是一看到Σ就要知道它是个矩阵。
复杂的例子
在上面我们已经对一个2维方阵进行了SVD分解,你可能会觉得分解出来的结果并没有什么特别吸引人的地方。 下面我们在一个维数更高的矩阵上进行SVD分解,这个矩阵如下,是一个7×5的矩阵:
\[\begin{bmatrix} 1 & 1 & 1 & 0 & 0\\ 2 & 2 & 2 & 0 & 0\\ 1 & 1 & 1 & 0 & 0\\ 5 & 5 & 5 & 0 & 0\\ 1 & 1 & 0 & 2 & 2\\ 0 & 0 & 0 & 3 & 3\\ 0 & 0 & 0 & 1 & 1 \end{bmatrix}\]与之前完全相同的代码,只是矩阵输入不同。
from numpy import *
Input = [[1, 1, 1, 0, 0],
[2, 2, 2, 0, 0],
[5, 5, 5, 0, 0],
[1, 1, 0, 2, 2],
[0, 0, 0, 1, 1]]
U, Sigma, VT = linalg.svd(Input)
print "U:\n" + U.__str__()
print "Sigma:\n" + Sigma.__str__()
print "VT:\n" + VT.__str__()
运行得到的结果如下:
U:
[[ -1.80935751e-01 -2.25101243e-02 9.42770408e-03 9.80646844e-01
7.06996105e-02]
[ -3.61871502e-01 -4.50202486e-02 1.88554082e-02 -8.65693529e-04
-9.30948934e-01]
[ -9.04678756e-01 -1.12550622e-01 4.71385204e-02 -1.95783091e-01
3.58239651e-01]
[ -1.33536443e-01 8.95928026e-01 -4.23651968e-01 5.55111512e-16
1.11022302e-16]
[ -5.96970569e-03 4.26745592e-01 9.04352012e-01 -1.14491749e-15
-3.33066907e-16]]
Sigma:
[ 9.56431204e+00 3.22455761e+00 3.55194920e-01 1.39082672e-15
0.00000000e+00]
VT:
[[ -5.81495977e-01 -5.81495977e-01 -5.67534028e-01 -2.85480640e-02
-2.85480640e-02]
[ 6.84200201e-02 6.84200201e-02 -2.09425233e-01 6.88032875e-01
6.88032875e-01]
[ -3.96460754e-01 -3.96460754e-01 7.96270180e-01 1.60610620e-01
1.60610620e-01]
[ 7.07106781e-01 -7.07106781e-01 4.85722573e-16 -5.55111512e-17
-5.55111512e-17]
[ 0.00000000e+00 -5.22363948e-17 5.05866788e-17 -7.07106781e-01
7.07106781e-01]]
继续观察Σ,我们发现其最后两个元素已经很小趋近于0了,根据之前的分解公式,它再与其它元素相乘结果还是为0, 那么我们不妨可以考虑把它们去掉。那么Σ就从原来的5维方阵降维到了3维。数据集可以近似这样表示:
\[Data_{m\times n}=U_{m\times 3}\Sigma _{3\times 3}V_{3\times n}\]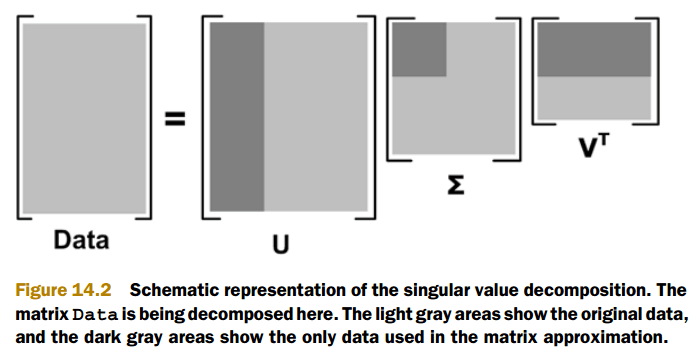
矩阵重构
下面我们试图根据经过降维的分解结果重构原始矩阵,看看效果怎么样。首先需要由Σ行向量构建对角阵,如下代码:
# Method 1
Sig3 = mat([[Sigma[0], 0, ],
[0, Sigma[1], 0],
[0, 0, Sigma[2]]])
# Method 2
Sig3 = mat(diag(Sigma[:3]))
这两种方法都可以实现我们的目标,第一种方法简单易懂,第二种方法通用性更强。当有成百上千的奇异值时,用方法2
无疑是最好的选择。需要解释的地方有[:3]表示取前三个元素,千万不要漏了:,要不然就变成取第三个元素了。
diag()用于生成对角阵,参数即为对角阵对角线上的元素。
mat()是numpy的函数,用于将Python里定义的二维数组转换成numpy的矩阵类型。构建好的Sig3如下:
[[ 9.56431204 0. 0. ]
[ 0. 3.22455761 0. ]
[ 0. 0. 0.35519492]]
然后我们需要按照公式进行计算。由于Σ变成3维,U取对应的前3列以及VT取前3行就行了。 我们可以将其与原始数据做差取绝对值作比较,可以得到如下结果:
RestoreData = U[:, :3] * Sig3 * VT[:3, :]
print "RestoredData:\n" + RestoreData.__str__()
Delta = abs(Input - RestoreData)
print "Delta:\n" + Delta.__str__()
输出结果如下:
RestoredData:
[[ 1.00000000e+00 1.00000000e+00 1.00000000e+00 -1.85290151e-16
-1.85290151e-16]
[ 2.00000000e+00 2.00000000e+00 2.00000000e+00 -6.96057795e-17
-6.96057795e-17]
[ 5.00000000e+00 5.00000000e+00 5.00000000e+00 -1.42247325e-16
-1.42247325e-16]
[ 1.00000000e+00 1.00000000e+00 -7.07767178e-16 2.00000000e+00
2.00000000e+00]
[ -8.32667268e-17 -1.41553436e-15 1.72084569e-15 1.00000000e+00
1.00000000e+00]]
Delta:
[[ 1.88737914e-15 1.44328993e-15 2.55351296e-15 1.85290151e-16
1.85290151e-16]
[ 1.11022302e-15 2.22044605e-16 1.11022302e-15 6.96057795e-17
6.96057795e-17]
[ 2.66453526e-15 8.88178420e-16 3.55271368e-15 1.42247325e-16
1.42247325e-16]
[ 1.11022302e-16 5.55111512e-16 7.07767178e-16 0.00000000e+00
0.00000000e+00]
[ 8.32667268e-17 1.41553436e-15 1.72084569e-15 1.11022302e-15
1.11022302e-15]]
可以看到“还原度”非常高,差别最大的也在10的-15次方量级,完全满足精度要求。 至此便完成了矩阵SVD分解的任务。通过三个矩阵对原始矩阵进行了近似,可以用 一个小很多的矩阵来表示一个大矩阵。
一个小问题
在刚刚的例子中,你会发现,我们选择保留了3个奇异值,舍去了两个。那为什么不保留2个或4个呢? 我们可以有很多启发式的策略。其中一个是保留矩阵中90%的能量信息。为了计算总能量信息, 我们可以将所有的奇异值求平方和,然后依次累加各奇异值的平方,直到累加到总值的90%为止。 另一个策略是,当矩阵有上万的奇异值时,那么就保留前2000或3000个。尽管后一种方法不太优雅, 但更容易实施。之所以说不够优雅是因为,在任何数据集上并不能保证前3000个奇异值就能够包含90%的 能量信息。我们可以自己编写一个函数用于计算当取多少元素时,保留的能量值大于90%。
完整代码
from numpy import *
def get_number(sigma, limit):
"""Get the number of items should be selected , not the index."""
return get_index(sigma, limit) + 1
def get_index(sigma, limit):
"""Get the index of the last item that should be selected."""
pow_sig = sigma * sigma
sum_ps = sum(pow_sig)
temp = 0
count = 0
for i in pow_sig:
temp += i
if temp > limit * sum_ps:
return count
break
count += 1
def get_accuracy(sigma, limit):
"""Calculate how much matrix energy kept."""
pow_sig = sigma * sigma
sum_ps = sum(pow_sig)
temp = 0
count = 0
for i in pow_sig:
temp += i
if temp > limit * sum_ps:
return temp / sum_ps
break
count += 1
def SVD(Input, limit):
"""SVD main function.Two arguments are required:
the input matrix and the keeping matrix energy rate."""
U, Sigma, VT = linalg.svd(Input)
print "U:\n" + U.__str__() + "\n"
print "Sigma:\n" + Sigma.__str__() + "\n"
print "VT:\n" + VT.__str__() + "\n"
Sig = mat(diag(Sigma[:get_number(Sigma, limit)]))
print "Select <" + get_number(Sigma, limit).__str__() + "> singular value(s).Represent " + (
get_accuracy(Sigma, limit) * 100).__str__() + " % energy.\n"
print "Sigma:\n" + Sig.__str__() + "\n"
RestoreData = U[:, :get_number(Sigma, limit)] * Sig * VT[:get_number(Sigma, limit), :]
print "RestoredData:\n" + RestoreData.__str__() + "\n"
Delta = abs(Input - RestoreData)
print "Delta:\n" + Delta.__str__()
return
Input = [[1, 1, 1, 0, 0],
[2, 2, 2, 0, 0],
[5, 5, 5, 0, 0],
[1, 1, 0, 2, 2],
[0, 0, 0, 1, 1]]
limit = 0.9
SVD(Input, limit)
我们把limit设置成0.9,即保留90%的矩阵能量,运算结果如下:
U:
[[ -1.80935751e-01 -2.25101243e-02 9.42770408e-03 9.80646844e-01
7.06996105e-02]
[ -3.61871502e-01 -4.50202486e-02 1.88554082e-02 -8.65693529e-04
-9.30948934e-01]
[ -9.04678756e-01 -1.12550622e-01 4.71385204e-02 -1.95783091e-01
3.58239651e-01]
[ -1.33536443e-01 8.95928026e-01 -4.23651968e-01 5.55111512e-16
1.11022302e-16]
[ -5.96970569e-03 4.26745592e-01 9.04352012e-01 -1.14491749e-15
-3.33066907e-16]]
Sigma:
[ 9.56431204e+00 3.22455761e+00 3.55194920e-01 1.39082672e-15
0.00000000e+00]
VT:
[[ -5.81495977e-01 -5.81495977e-01 -5.67534028e-01 -2.85480640e-02
-2.85480640e-02]
[ 6.84200201e-02 6.84200201e-02 -2.09425233e-01 6.88032875e-01
6.88032875e-01]
[ -3.96460754e-01 -3.96460754e-01 7.96270180e-01 1.60610620e-01
1.60610620e-01]
[ 7.07106781e-01 -7.07106781e-01 4.85722573e-16 -5.55111512e-17
-5.55111512e-17]
[ 0.00000000e+00 -5.22363948e-17 5.05866788e-17 -7.07106781e-01
7.07106781e-01]]
Select <2> singular value(s).Represent 99.8763103619 % energy.
Sigma:
[[ 9.56431204 0. ]
[ 0. 3.22455761]]
RestoredData:
[[ 1.00132762e+00 1.00132762e+00 9.97333552e-01 -5.37832382e-04
-5.37832382e-04]
[ 2.00265523e+00 2.00265523e+00 1.99466710e+00 -1.07566476e-03
-1.07566476e-03]
[ 5.00663809e+00 5.00663809e+00 4.98666776e+00 -2.68916191e-03
-2.68916191e-03]
[ 9.40340972e-01 9.40340972e-01 1.19821962e-01 2.02416853e+00
2.02416853e+00]
[ 1.27351615e-01 1.27351615e-01 -2.55778895e-01 9.48408457e-01
9.48408457e-01]]
Delta:
[[ 0.00132762 0.00132762 0.00266645 0.00053783 0.00053783]
[ 0.00265523 0.00265523 0.0053329 0.00107566 0.00107566]
[ 0.00663809 0.00663809 0.01333224 0.00268916 0.00268916]
[ 0.05965903 0.05965903 0.11982196 0.02416853 0.02416853]
[ 0.12735161 0.12735161 0.25577889 0.05159154 0.05159154]]
本文作者原创,未经许可不得转载,谢谢配合
