几何变换
图像缩放
对于图像缩放,可以使用cv2.resize()实现。参数可以是设定缩放的倍数,也可以直接是缩放后的图像大小。
同时还要设置插值的方法。在缩小时推荐使用cv2.INTER_AREA,在扩展时推荐使用cv2.INTER_CUBIC(慢)和
cv2.INTER_LINEAR。默认情况下改变图像尺寸大小的插值方法都是cv2.INTER_LINEAR。
img = cv2.imread("E:\\600.jpg")
# 第一个参数是原始图像
# 第二个参数是输出图像的大小,因为后面指定了缩放倍数,所以这里为None
# 第三个参数是x方向的缩放倍数
# 第四个参数是y方向的缩放倍数
# 第五个参数是插值的方法,这里使用了三次插值法
res1 = cv2.resize(img, None, fx=1.5, fy=1.5, interpolation=cv2.INTER_CUBIC)
# 第二种方法,直接指定输出图像的大小,不设置缩放比例
height, width = img.shape[:2]
res2 = cv2.resize(img, (2 * width, 2 * height), interpolation=cv2.INTER_CUBIC)
cv2.imshow("img", img)
cv2.imshow("res1", res1)
cv2.imshow("res2", res2)
cv2.waitKey(0)
基于此我们可以将之前的视频进行缩放,代码如下:
cap = cv2.VideoCapture(0)
while cap.isOpened():
ret, frame = cap.read()
resize_frame = cv2.resize(frame, None, fx=0.5, fy=0.5, interpolation=cv2.INTER_CUBIC)
cv2.imshow("resize", resize_frame)
k = cv2.waitKey(1) & 0xFF
if k == 27:
break
cap.release()
上述代码将摄像头捕获到的每帧都缩小成了原来的1/4。
图像平移
我们可以使用平移矩阵对图像进行平移操作,调用cv2.warpAffine()完成。矩阵如下:
其中tx、ty表示沿x和y方向的偏移量。
cap = cv2.VideoCapture(0)
# 建立一个M矩阵,表示沿x方向平移100像素,沿y方向平移50像素
M = np.float32([[1, 0, 100],
[0, 1, 50]])
while cap.isOpened():
ret, frame = cap.read()
# 三个参数依次为输入图像、平移矩阵以及输出图像大小
move = cv2.warpAffine(frame, M, (frame.shape[1], frame.shape[0]))
cv2.imshow("frame", frame)
cv2.imshow("move", move)
k = cv2.waitKey(1) & 0xFF
if k == 27:
break
cap.release()
上述代码对视频进行了(100,50)的平移。效果如下:
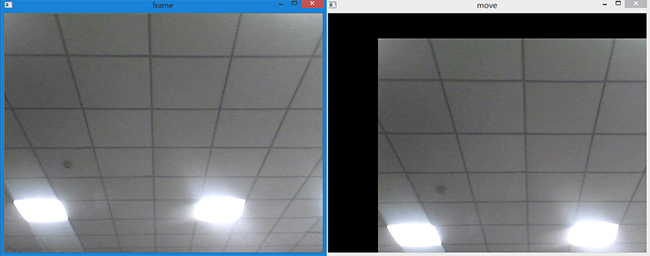
图像旋转
对于图像旋转,同样适用cv2.warpAffine()函数进行。只不过需要修改刚刚构建的M矩阵。
但OpenCV为了方便,已经定义了cv2.getRotationMatrix2D()用于生成M矩阵。实例代码如下:
cap = cv2.VideoCapture(0)
width = int(cap.get(3))
height = int(cap.get(4))
# 第一个参数是旋转中心,这里设置为图片中心
# 第二个参数是旋转角度
# 第三个参数是旋转后的缩放因子
# 可以通过设置这三个参数来控制旋转后超出边界的问题
M = cv2.getRotationMatrix2D((width / 2, height / 2), 45, 0.6)
while cap.isOpened():
ret, frame = cap.read()
# 三个参数依次为输入图像、旋转矩阵以及输出图像大小
rotate = cv2.warpAffine(frame, M, (width, height))
cv2.imshow("frame", frame)
cv2.imshow("rotate", rotate)
k = cv2.waitKey(1) & 0xFF
if k == 27:
break
cap.release()
上述代码我们实现了视频的实时旋转,效果如下图所示:
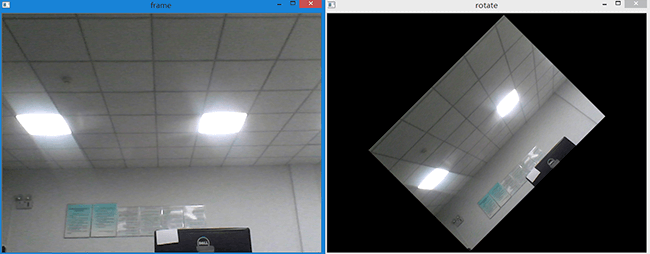
仿射变换
同样,我们使用cv2.warpAffine()函数进行仿射变换。所谓仿射变换,其特点是原图中所有的
平行线在结果图中同样平行。其实放射变换包括了上面的缩放、平移和旋转。所以上面提到的M矩阵
其实就是变换矩阵。只不过我们限定了一次只改变与平移、缩放或旋转有关的量。在OpenCV中,仿射变换
只需要一行代码即可实现,十分简单。但这是远远不够的,我们必须要知道其变换原理。所以在介绍OpenCV的
仿射变换之前,先介绍一些仿射变换的基础知识与原理。也正如前面所说,平移、缩放和旋转其实都是仿射变换
的特例。通过我们使用的函数其实也都能看出来,函数名都是一样的,只是传入的参数M不同。掌握了仿射变换原理
也就掌握了上面说的平移、缩放与旋转。
仿射变换原理
仿射变换(Affine transformation或Affine Map)是一种二维坐标到二维坐标的线性变换,它保持了 二维图形的“平直性”(直线经过变换后仍然是直线),和“平行性”(二维图形之间的相对位置关系不变, 平行线依然是平行线,且直线上点的位置顺序不变)。可以写成如下形式:
\[\left\{\begin{matrix} x^{'}=ax+by+m \\ y^{'}=cx+dy+n \end{matrix}\right.\]也可以用矩阵的形式表示,写成如下形式:
\[\begin{bmatrix} u\\v \end{bmatrix}=\begin{bmatrix} a_{2} & a_{1} & a_{0}\\ b_{2} & b_{1} & b_{0} \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix}\]或者这样:
\[\begin{bmatrix} x^{'}\\y^{'} \\ 1 \end{bmatrix}=\begin{bmatrix} a_{2} & a_{1} & a_{0}\\ b_{2} & b_{1} & b_{0}\\ 0 &0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix}\]它可以通过一系列原子变换的复合来实现,包括平移(Translation)、缩放(Scale)、
旋转(Rotation)、翻转(Flip)以及错切(Shear)。不共线的三对点决定了一个唯一的仿射变换。
常用的仿射变换如下:
平移,将每一点移动到(x+tx,y+ty)。
缩放,将横坐标缩放sx倍,纵坐标缩放sy倍。
\[\begin{bmatrix} 1& 0 & sx\\ 0& 1 & sy\\ 0& 0 & 1 \end{bmatrix}\]旋转,图像围绕原点顺时针旋转θ度。
\[\begin{bmatrix} cos\theta& -sin\theta & 0\\ sin\theta& cos\theta & 0\\ 0& 0 & 1 \end{bmatrix}\]旋转(指定旋转中心),图像以(x,y)为旋转中心顺时针旋转θ。
\[\begin{bmatrix} cos\theta& -sin\theta & x-xcos\theta+ysin\theta\\ sin\theta& cos\theta & y-xsin\theta-ycos\theta\\ 0& 0 & 1 \end{bmatrix}\]OpenCV仿射变换
在OpenCV中,首先给出了一个函数(cv2.getAffineTransform())用于构造一个2×3的矩阵M。
它接受的参数是变换前后的两组对应坐标。如下:
pts1 = np.float32([[50, 50], [200, 50], [50, 200]])
pts2 = np.float32([[10, 100], [200, 50], [100, 250]])
M = cv2.getAffineTransform(pts1, pts2)
第一个参数是变换前的坐标,第二个参数是变换后的坐标。在构造完M矩阵后,便可以和之前一样使用
cv2.warpAffine()函数了,如下:
cap = cv2.VideoCapture(0)
width = int(cap.get(3))
height = int(cap.get(4))
pts1 = np.float32([[50, 50], [200, 50], [50, 200]])
pts2 = np.float32([[10, 100], [200, 50], [100, 250]])
M = cv2.getAffineTransform(pts1, pts2)
while cap.isOpened():
ret, frame = cap.read()
# 三个参数依次为输入图像、变换矩阵以及输出图像大小
transform = cv2.warpAffine(frame, M, (width, height))
cv2.imshow("frame", frame)
cv2.imshow("transform", transform)
k = cv2.waitKey(1) & 0xFF
if k == 27:
break
cap.release()
透视变换
对于视角变换,我们需要一个3×3的变换矩阵。这和仿射变换是不同的。我们需要在图像上找到4个点 以及他们在输出图像上的对应坐标。这四个点中任意三个不能共线。与仿射变换类似,在OpenCV中 同样为我们准备好了构造M矩阵的函数,而我们要做的就是把4组对应点告诉程序。
cap = cv2.VideoCapture(0)
width = int(cap.get(3))
height = int(cap.get(4))
pts1 = np.float32([[56, 65], [368, 52], [28, 387], [389, 390]])
pts2 = np.float32([[0, 0], [300, 0], [0, 300], [300, 300]])
M = cv2.getPerspectiveTransform(pts1, pts2)
while cap.isOpened():
ret, frame = cap.read()
# 三个参数依次为输入图像、变换矩阵以及输出图像大小
transform = cv2.warpPerspective(frame, M, (width, height))
cv2.imshow("frame", frame)
cv2.imshow("transform", transform)
k = cv2.waitKey(1) & 0xFF
if k == 27:
break
cap.release()
可以看到,整段代码除了构造M矩阵不同外,其余和仿射变换在流程上几乎没有任何差别。
本文作者原创,未经许可不得转载,谢谢配合
