图像阈值
简单阈值
正如它的名字，直接根据给定的阈值进行判断，大于则为1，小于则为0。之前使用的熟悉的阈值函数cv2.threshold()便是这种。
这里简单回顾。其第一个参数是需要二值化的图像，第二个参数是阈值，第三个参数是当像素值高于（或小于）阈值时应该被赋予的
新像素值。OpenCV提供了多种不同的阈值方法。我们之前用的便是cv2.THRESH_BINARY。函数的返回值有两个，第二个即为二值化
以后的图像。因此不能只用一个变量接收这个函数的返回值，否则会报错的。同时需要注意的是，传入函数的图像应该是灰度图像，
而不是RGB图像，RGB的话需要先转换成灰度再传入，否则可能得到的不是你想要的结果。
# coding= utf-8
import numpy as np
import cv2
from matplotlib import pyplot as plt
gray = cv2.imread("E:\\gray.png")
ret, thresh1 = cv2.threshold(gray, 128, 255, cv2.THRESH_BINARY)
ret, thresh2 = cv2.threshold(gray, 128, 255, cv2.THRESH_BINARY_INV)
ret, thresh3 = cv2.threshold(gray, 128, 255, cv2.THRESH_TRUNC)
ret, thresh4 = cv2.threshold(gray, 128, 255, cv2.THRESH_TOZERO)
ret, thresh5 = cv2.threshold(gray, 128, 255, cv2.THRESH_TOZERO_INV)
titles = ['original', 'binary', 'binary_inv', 'trunc', 'tozero', 'tozero_inv']
imgs = [gray, thresh1, thresh2, thresh3, thresh4, thresh5]
for i in xrange(6):
plt.subplot(3, 2, i + 1), plt.imshow(imgs[i], 'gray')
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
这里我们使用了显示多幅图像的新的更简便的方式。在之前，我们采用OpenCV的内置拼图功能进行绘制。
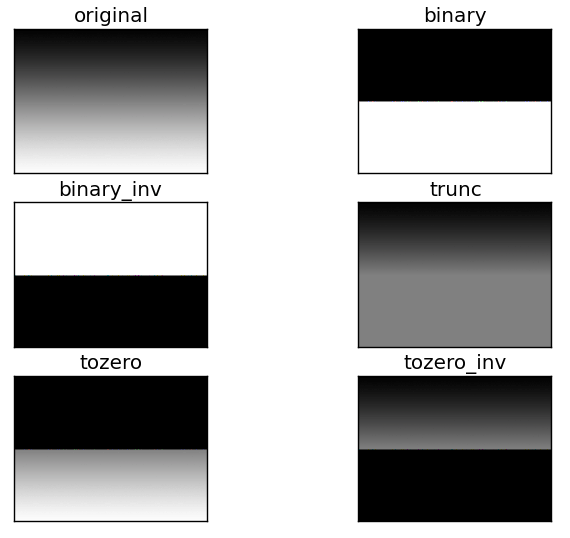
现在，我们可以借助matplotlib包的绘图功能进行多幅图的绘制。不同的阈值模式对应的效果如下，
今后在使用的过程中需要什么样的效果可以进行比对。
自适应阈值
前面我们讨论的简单阈值，也即通过对整幅图像指定一个固定的阈值对图像进行二值化。但显然有时这是不合适的，
尤其是当图像的不同部分有不同的亮度时。例如拍照的某一页书本，由于光照的原因整体偏灰。这个时候我们如果
指定128为阈值，很有可能就无法正确区分出文字和背景了。因为背景的灰度低于128，从而无法识别。这时自适应
阈值便派上用场了。自适应阈值时根据图像上的每个小区域计算与其对应的阈值。因此在同一幅图像上不同区域采用
的是不同的阈值，从而使我们能在亮度不同的情况下得到更好的结果。OpenCV中自适应阈值采用cv2.adaptiveThreshold()
函数实现。使用时我们需要指定计算阈值的方法(Adaptive Method)，OpenCV中内置了两种，分别是cv2.ADAPTIVE_THRESH_MEAN_C和cv2.ADAPTIVE_THRESH_GAUSSIAN_C。
MEAN_C方法很简单，阈值即取相邻领域的平均值。GAUSSIAN_C方法阈值同样取自相邻领域，只是不再是平均值，而是加权平均，
权重为一个高斯窗口。所谓高斯窗口就是要让窗口服从二维的高斯正态分布。3×3和5×5的高斯窗口如下图。
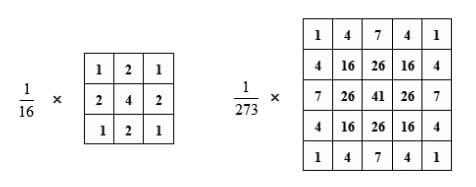其次我们还需要指定领域(Block Size)的大小。最后，我们需要指定一个常数C，最终的阈值即为领域平均值或加权平均值再减去
这个常数。示例代码如下：
# coding= utf-8
import numpy as np
import cv2
img = cv2.imread("E:\\600.jpg")
resize = cv2.resize(img, None, fx=0.6, fy=0.6, interpolation=cv2.INTER_CUBIC)
gray = cv2.cvtColor(resize, cv2.COLOR_BGR2GRAY)
ret, th1 = cv2.threshold(gray, 128, 255, cv2.THRESH_BINARY)
# 第一个参数是需要二值化的图像，注意要是灰度图
# 第二个参数是大于阈值时应该被赋予的值
# 第三个参数是阈值计算方法，MEAN或GAUSSIAN二选一
# 第四个参数是阈值显示方法，只能是BINARY或BINARY_INV二选一
# 第五个参数是领域大小，注意必须是奇数
# 第六个参数是自定义的常数
th2 = cv2.adaptiveThreshold(gray, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, 9, 2)
th3 = cv2.adaptiveThreshold(gray, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 9, 2)
cv2.imshow("original", resize)
cv2.imshow("th_binary", th1)
cv2.imshow("mean", th2)
cv2.imshow("gauss", th3)
cv2.waitKey(0)
对比效果如下：
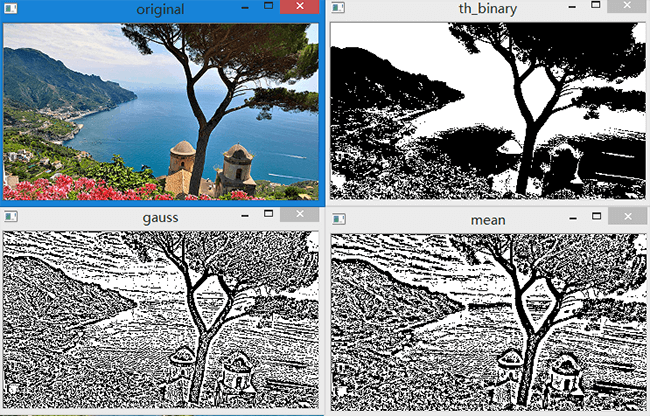同时不同的领域大小及常数都会对二值化结果造成影响。下面以Gauss为例，对比不同领域及常数的效果如下。
不同领域大小
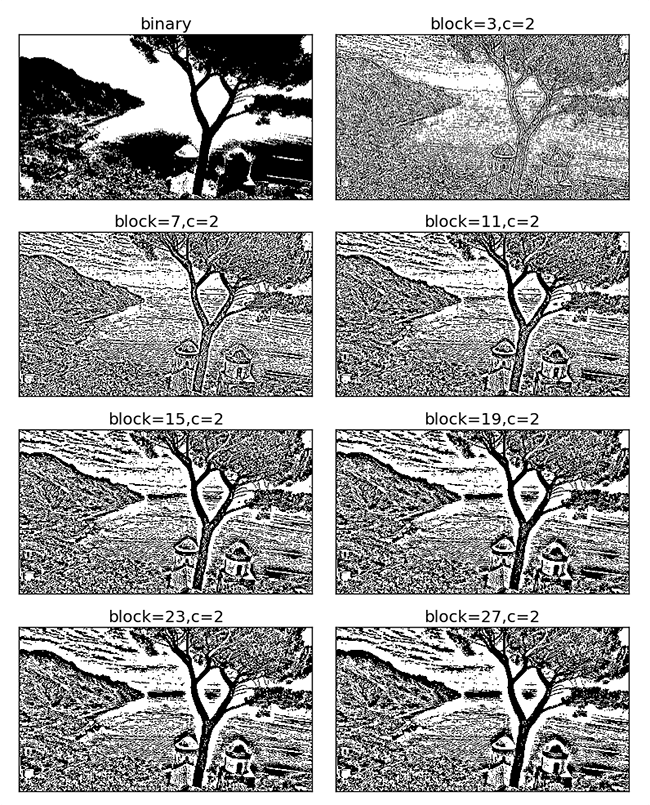可以看到当领域越来越大时，其保留的细节就越来越少，二值化的结果越来越“集中”。
block=3时保留了原图中非常多的细节。而block=27时树干部分已经看不出什么细节了。
不同常数大小
可以看到当常数越来越大时，二值化图像中白色部分就越来越多。这也很好理解。因为最终的阈值
是根据领域的平均值再减去这个常数得到的。所以常数越大，对应的最终阈值就会越小，而阈值越小，
也即白色的部分就会越多。
Otsu’s二值化
在前面使用阈值函数cv2.threshold()时说过，返回值有两个，一个是retVal，一个是二值化后的图像。
其中retVal当时说表示的是我们手动设定的阈值。现在在Otsu’s二值化中，这个返回值便有了新的含义。
Otsu’s简单来说就是对一幅双峰图像自动根据其灰度分布直方图计算出一个最合适的二值化阈值。对于非
双峰图像，这种方法的效果可能不理想。
在使用时，我们需要多传入一个参数:cv2.THRESH_OTSU，并且要把阈值设为0。然后程序便会根据算法找到
最优阈值，并返回给retVal。如果不使用Otsu二值化，返回的值便于我们设定的相等。
# coding=utf-8
import numpy as np
import cv2
from matplotlib import pyplot as plt
# 这里直接以灰度的方式打开图片，避免再转换的麻烦
img = cv2.imread("E:\\400.jpg", 0)
# 注意还要再加上一个参数
ret1, th1 = cv2.threshold(img, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
ret2, th2 = cv2.threshold(img, 128, 255, cv2.THRESH_BINARY)
print ret1, ret2
titles = ['otsu', 'binary_128']
imgs = [th1, th2]
for i in range(2):
plt.subplot(1, 2, i + 1), plt.imshow(imgs[i], 'gray')
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
对同一幅图片，指定阈值和使用Otsu’s二值化对比如下所示：
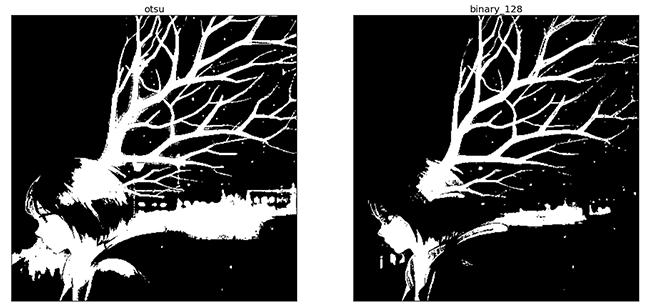可以看到，相较于指定固定阈值，Otsu’s方法更好。
Otsu’s二值化原理
核心思想其实很简单。由于Otsu’s针对的是双峰图，所以目的就是要找到一个阈值t，将这两峰分开，同时使得 峰内的方差最小。这样便可以将两峰最大化的分开，类似于分类问题。目标函数如下：
\[\sigma _{w}^{2}=q_{1}(t)\sigma_{1}^{2}(t)+q_{2}\sigma_{2}^{2}(t)\]寻找一个最合适的t，使得上式最小。其中：
\[q_{1}(t)= \sum_{i=1}^{t}P(i)\] \[q_{2}(t)= \sum_{i=t+1}^{I}P(i)\] \[\mu_{1}(t)=\sum_{i=1}^{t}\frac{iP(i)}{q_{1}(t)}\] \[\mu_{2}(t)=\sum_{i=t+1}^{I}\frac{iP(i)}{q_{2}(t)}\] \[\sigma_{1}^{2}(t)=\sum_{i=1}^{t}[i-\mu_{1}(t)]^{2}\frac{P(i)}{q_{1}(t)}\] \[\sigma_{2}^{2}(t)=\sum_{i=t+1}^{I}[i-\mu_{2}(t)]^{2}\frac{P(i)}{q_{2}(t)}\]图像平滑
2D卷积
我们可以对图像实施低通滤波(LPF)、高通滤波(HPF)等。LPF帮助我们去除噪声，模糊图像。
HPF则相反，帮助我们找到图像边缘，锐化图像。在OpenCV中，提供了cv2.filter2D()函数
供我们进行2D卷积。例如我们使用一个3×3的平均滤波器(9个位置上都是1/9，和为1)。
img = cv2.imread("E:\\350.jpg")
# 利用Numpy生成一个3×3的矩阵作为卷积核
kernel = np.ones((3, 3), np.float32) / 9
# 第一个参数是要处理的图片
# 第二个参数是用于设置输出图像的位深度，-1表示与原图保持一致
# 第三个参数是卷积核
dst = cv2.filter2D(img, -1, kernel)
cv2.imshow("img", img)
cv2.imshow("dst", dst)
cv2.waitKey(0)
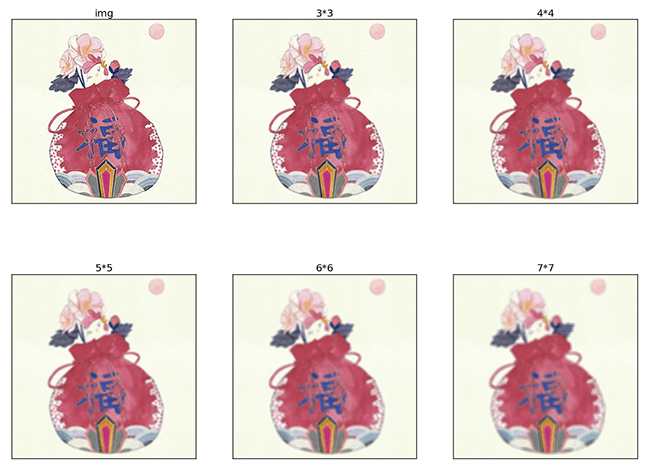
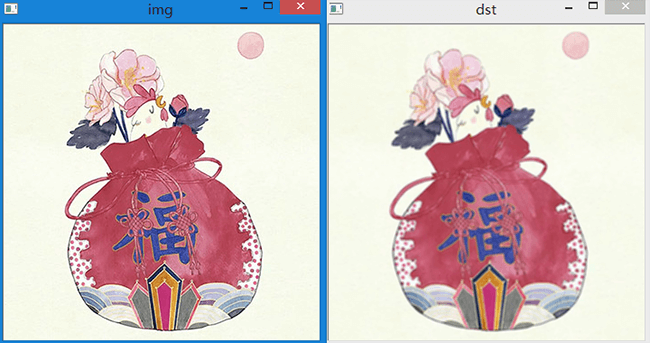通过对比图可以发现，相比于原图图像变模糊了。我们还可以设置不同的卷积核大小，
会产生不同的效果。卷积核越大，输出图像越模糊。
# coding=utf-8
import numpy as np
import cv2
from matplotlib import pyplot as plt
img = cv2.imread("E:\\350.jpg")
# 正如前面说到的OpenCV中读取的方式是BGR，而matplotlib的方式是RGB，所以需要给通道顺序调整一下
b, g, r = cv2.split(img)
img = cv2.merge([r, g, b])
kernel1 = np.ones((3, 3), np.float32) / 9
kernel2 = np.ones((4, 4), np.float32) / 16
kernel3 = np.ones((5, 5), np.float32) / 25
kernel4 = np.ones((6, 6), np.float32) / 36
kernel5 = np.ones((7, 7), np.float32) / 49
dst1 = cv2.filter2D(img, -1, kernel1)
dst2 = cv2.filter2D(img, -1, kernel2)
dst3 = cv2.filter2D(img, -1, kernel3)
dst4 = cv2.filter2D(img, -1, kernel4)
dst5 = cv2.filter2D(img, -1, kernel5)
titles = ['img', '3*3', '4*4', '5*5', '6*6', '7*7']
imgs = [img, dst1, dst2, dst3, dst4, dst5]
for i in range(6):
plt.subplot(2, 3, i + 1), plt.imshow(imgs[i], 'gray')
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
图像模糊
如前面的效果展示，使用低通滤波器可以达到图像模糊的目的，用于消除噪声。其实质就是 去除图像中的高频成分(噪声、边界等等)。所以边界也会变得模糊一些，当然有些技术不会 模糊边界。在OpenCV中提供了四种模糊方法。对于去除高频成分可以这样理解，图像的灰度 从0到255，灰度值越高可以认为其频率越高，低通滤波器的目的就是使突出的那些灰度尽量 少，大家都保持差不多的灰度。
平均
平均模糊使用归一化卷积核完成，也即卷积核的所有元素相加最终等于1。核心思想是将卷积核
覆盖的所有像素求平均值，并将这个值作为结果赋给中心像素。可以使用cv2.blur()或cv2.boxFilter()
实现。如果不想使用归一化卷积核，那么应该用后者，并且设置参数normalize = False。
下面的代码实现了与上面同样的功能。其实我们完全可以用cv2.filter2D()来实现，但是使用
cv2.blur()函数会更加方便，省去了自定义卷积核的麻烦。当然凡事有利有弊，这样自定义性就不如
自己写卷积核高了。所以如果自己设计了新的、OpenCV中没有的卷积核，还是建议使用filter2D()，
而对于OpenCV中已有的卷积核，大可不必再重新去写。直接用封装好的函数就好，可以提升编程效率。
img = cv2.imread("E:\\350.jpg")
# 第一个参数是待处理的图像
# 第二个参数是卷积核的大小
dst = cv2.blur(img, (5, 5))
cv2.imshow("dst", dst)
cv2.waitKey(0)
高斯模糊
其原理与平均滤波相同，但唯一不同的是这里变成了加权平均。而这个权则是服从二维高斯分布的。
使用cv2.GaussianBlur()实现。需要指定高斯核的大小(宽高，必须是奇数)，还有高斯函数沿X、
Y方向的标准差。如果只指定了一个方向的标准差，那么另一个方向默认相同。如果两个标准差都是0，
函数会根据核函数的大小自己计算。高斯滤波可以有效地去除高斯噪音。当然如果你愿意的话，
可以使用函数cv2.getGaussianKernel()自己构建一个高斯核。
img = cv2.imread("E:\\1000.jpg")
# 第一个参数是待处理的图像
# 第二个参数是卷积核的大小
# 第三个参数是标准差
dst = cv2.GaussianBlur(img[:225, :450, :], (65, 65), 0)
img[:225, :450, :] = dst
cv2.putText(img, "This is GaussianBlur", (70, 112), cv2.FONT_HERSHEY_SIMPLEX, 1, (255, 255, 255), 2, cv2.LINE_AA)
cv2.imshow("dst", img)
cv2.waitKey(0)
高斯模糊应用十分广泛，我们很多时候在手机、网页上看到的模糊背景都是采用高斯模糊做出来的。
通过高斯模糊搭配其它效果可以做出很有艺术感的背景。如下图所示，是高斯模糊的效果：
中值模糊
所谓中值模糊是用于卷积核对应像素的中值来代替中心像素值。这个滤波器常用来去除椒盐噪声。
前面说的滤波器都是根据周围像素计算出一个新的值来代替中心像素原有值，而中值滤波使用中心像素
周围的像素值的中值代替。使用cv2.medianBlur()实现。注意卷积核大小应该是奇数。
img = cv2.imread("E:\\1000.jpg")
# 第一个参数是待处理的图像
# 第二个参数是卷积核的大小
dst = cv2.medianBlur(img, 9)
cv2.imshow("dst", dst)
cv2.waitKey(0)
效果如下图所示：
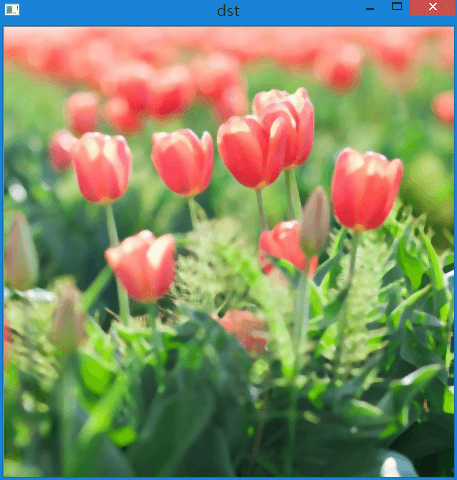可以看到中值滤波和高斯滤波的“画风”还是有区别的。中值滤波有一种油画的感觉。这从原理上也能解释得通。
因为中值滤波取的是周围像素的中值，因此在某一小范围内，其周围的像素值变化都不大，所以导致了中值都
很接近，形成了“块状”的颜色，而这正类似于油画的效果。
此外还可以测试去除椒盐噪声的效果，如下所示：
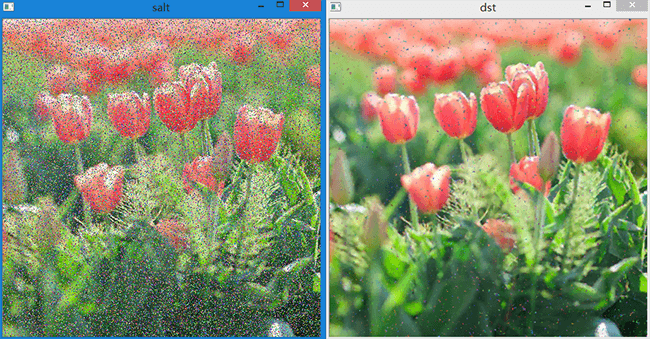我们利用之前编写的为图像添加椒盐噪声的函数向一幅450×450的图像中添加了70000个椒盐噪声。
图片总像素为202500，噪声比例约为34.6%。我们利用3领域的中值滤波进行处理，可以看到效果非常好，已经去除绝大部分噪声了。
双边滤波
函数cv2.bilateralFilter()能在保持边界清晰的情况下有效的去除噪音。但是这种操作与其他滤波器相比会比较慢。
我们已经知道高斯滤波器是求中心点邻近区域像素的高斯加权平均值。这种高斯滤波器只考虑像素之间的空间关系，
而不会考虑像素值之间的关系（像素的相似度）。所以这种方法不会考虑一个像素是否位于边界。因此边界也会别模糊掉，
而这正不是我们想要。双边滤波在同时使用空间高斯权重和灰度值相似性高斯权重。空间高斯函数确保只有邻近区域的像素
对中心点有影响，灰度值相似性高斯函数确保只有与中心像素灰度值相近的才会被用来做模糊运算。所以这种方法会确保边界不
会被模糊掉，因为边界处的灰度值变化比较大。演示代码如下：
img = cv2.imread("E:\\bin5.png")
# 第一个参数是待处理图像
# 第二个参数是领域直径范围
# 第三个参数是空间高斯函数标准差
# 第四个参数是灰度值相似性高斯函数标准差
img2 = cv2.bilateralFilter(img, 9, 75, 75)
cv2.imshow("img", img)
cv2.imshow("img2", img2)
cv2.waitKey(0)
效果如下：
可以看到，布料中的纹理被模糊掉了，但是其边界还是清晰的。而且黄色的纸张上面的噪声也过滤掉了，变得更加干净了。
因此双边滤波可以用于对纹理进行剔除，同时又可以较好地保留边界。
图像噪声
图像噪声有很多种，这里主要介绍两种，椒盐噪声和高斯噪声，且要区别一下椒盐噪声和高斯噪声。介绍噪声之前先介绍一下信噪比。
我们使用信噪比（Signal NoiseRate）衡量图像噪声，对于一幅灰度图像有如下公式：
SNR=（洁净图片中的像素点的灰度值之和）/abs（噪声图片的灰度值之和-洁净图片中的灰度值之和）
椒盐噪声
椒盐噪声是出现在随机位置、噪点深度基本固定的噪声，高斯噪声与其相反，是几乎每个点上都出现噪声、噪点深度随机的噪声。
椒盐噪声也称为脉冲噪声，包含两种噪声，一种是盐噪声（salt noise），另一种是胡椒噪声（pepper noise）。
盐=白色，椒=黑色。前者是高灰度噪声，后者属于低灰度噪声。一般两种噪声同时出现，呈现在图像上就是黑白杂点。
所以从这个角度来看，我们之前写的那个添加椒盐噪声的函数的模式中，彩色的噪声不能算是严格意义上的椒盐噪声。
给一副数字图像加上椒盐噪声的步骤如下：
- （1）指定信噪比 SNR （其取值范围在[0, 1]之间）
- （2）计算总像素数目 SP， 得到要加噪的像素数目 NP = SP * (1-SNR)
- （3）随机获取要加噪的每个像素位置P（i, j）
- （4）指定像素值为255或者0。
- （5）重复3,4两个步骤完成所有像素的NP个像素
- （6）输出加噪以后的图像
我们在之前直接指定噪声个数其实也是可以的，相当于直接到了第二步。
高斯噪声
高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。
与椒盐噪声相似（Salt And Pepper Noise），高斯噪声（gauss noise）也是数字图像的一个常见噪声。
椒盐噪声是出现在随机位置、噪点深度基本固定的噪声，高斯噪声与其相反，是几乎每个点上都出现噪声、噪点深度随机的噪声。
所以也就是说高斯噪声的“高斯”体现在其噪点深度上，而不是其位置上。
在Python中，有产生高斯随机数的方法。random.gauss(mu, sigma)。mu是均值，sigma是标准差。给一幅图像添加高斯噪声步骤如下：
-
(1)设定参数sigma 和 Xmean
-
(2)产生一个高斯随机数
-
(3)根据输入像素计算出输出像素
-
(4)重新将像素值限制或放缩在[0 ~ 255]之间
-
(5)循环所有像素
-
(6)输出图像。
实现代码如下：
def gaussNoise(img, mu, sigma):
# 首先创建一个新的图像用于存放处理后的结果
img2 = np.zeros(img.shape, np.uint8)
# 获取原始图像的宽高
row = img.shape[0]
col = img.shape[1]
for i in range(row):
for j in range(col):
# 依次循环图像中的每个像素，BGR三个通道分别处理
b = img[i, j, 0] + random.gauss(mu, sigma)
g = img[i, j, 1] + random.gauss(mu, sigma)
r = img[i, j, 2] + random.gauss(mu, sigma)
# 判断处理后的值是否越界
if b > 255:
b = 255
if b < 0:
b = 0
if g > 255:
g = 255
if g < 0:
g = 0
if r > 255:
r = 255
if r < 0:
r = 0
# 将新的像素值赋给新的图像
img2[i, j, 0] = b
img2[i, j, 1] = g
img2[i, j, 2] = r
return img2
img = cv2.imread("E:\\bin5.png")
img2 = gaussNoise(img, 0, 25)
cv2.imshow("img", img)
cv2.imshow("img2", img2)
cv2.waitKey(0)
产生结果如下：
高斯函数的mu和sigma影响最后的结果，总的来说，mu决定输出图像的亮度，sigma决定输出图像噪声的强弱。如下对比图：
最后，附上椒盐噪声与高斯噪声的对比图及完整代码，如下：
# coding=utf-8
import numpy as np
import cv2
import random
from matplotlib import pyplot as plt
def gaussNoise(img, mu, sigma):
# 首先创建一个新的图像用于存放处理后的结果
img2 = np.zeros(img.shape, np.uint8)
# 获取原始图像的宽高
row = img.shape[0]
col = img.shape[1]
for i in range(row):
for j in range(col):
# 依次循环图像中的每个像素，BGR三个通道分别处理
b = img[i, j, 0] + random.gauss(mu, sigma)
g = img[i, j, 1] + random.gauss(mu, sigma)
r = img[i, j, 2] + random.gauss(mu, sigma)
# 判断处理后的值是否越界
if b > 255:
b = 255
if b < 0:
b = 0
if g > 255:
g = 255
if g < 0:
g = 0
if r > 255:
r = 255
if r < 0:
r = 0
# 将新的像素值赋给新的图像
img2[i, j, 0] = b
img2[i, j, 1] = g
img2[i, j, 2] = r
return img2
def peppersalt(img, n, m):
"""
Add peppersalt to image
:param img: the image you want to add noise
:param n: the total number of noise (0 <= n <= width*height)
:param m: different mode
m=1:add only white noise in whole image
m=2:add only black noise in whole image
m=3:add black and white noise in whole image
m=4:add gray scale noise range from 0 to 255
m=5:add color noise in whole image,RGB is combined randomly with every channel ranges from 0 to 255
:return: the processed image
"""
img2 = np.zeros(img.shape, np.uint8)
img2[:, :, 0] = img[:, :, 0]
img2[:, :, 1] = img[:, :, 1]
img2[:, :, 2] = img[:, :, 2]
if m == 1:
for i in range(n):
x = int(np.random.random() * img.shape[0])
y = int(np.random.random() * img.shape[1])
img2[x, y, 0] = 255
img2[x, y, 1] = 255
img2[x, y, 2] = 255
elif m == 2:
for i in range(n):
x = int(np.random.random() * img.shape[0])
y = int(np.random.random() * img.shape[1])
img2[x, y, 0] = 0
img2[x, y, 1] = 0
img2[x, y, 2] = 0
elif m == 3:
for i in range(n):
x = int(np.random.random() * img.shape[0])
y = int(np.random.random() * img.shape[1])
flag = np.random.random() * 255
if flag > 128:
img2[x, y, 0] = 255
img2[x, y, 1] = 255
img2[x, y, 2] = 255
else:
img2[x, y, 0] = 0
img2[x, y, 1] = 0
img2[x, y, 2] = 0
elif m == 4:
for i in range(n):
x = int(np.random.random() * img.shape[0])
y = int(np.random.random() * img.shape[1])
flag = int(np.random.random() * 255)
img2[x, y, 0] = flag
img2[x, y, 1] = flag
img2[x, y, 2] = flag
elif m == 5:
for i in range(n):
x = int(np.random.random() * img.shape[0])
y = int(np.random.random() * img.shape[1])
f1 = int(np.random.random() * 255)
f2 = int(np.random.random() * 255)
f3 = int(np.random.random() * 255)
img2[x, y, 0] = f1
img2[x, y, 1] = f2
img2[x, y, 2] = f3
return img2
temp = cv2.imread("E:\\bin5.png")
# 用于BGR到RGB的转换，否则matplotlib显示的颜色不对
ori = np.zeros(temp.shape, np.uint8)
ori[:, :, 0] = temp[:, :, 2]
ori[:, :, 1] = temp[:, :, 1]
ori[:, :, 2] = temp[:, :, 0]
img1 = ori
img3 = gaussNoise(ori, 0, 25)
img2 = peppersalt(ori, 5000, 3)
titles = ['original', 'salt(n=7000)', 'gauss(m=0,s=25)']
imgs = [img1, img2, img3]
for i in range(3):
plt.subplot(1, 3, i + 1), plt.imshow(imgs[i], 'gray')
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
通过对比图，可以清楚地发现椒盐噪声和高斯噪声的区别。椒盐噪声有很强烈的黑白点，
高斯噪声更像是平时拍照时产生的噪点。
本文作者原创,未经许可不得转载,谢谢配合
