图像金字塔
所谓图像金字塔很好理解,就是一组具有不同分辨率的原始图像,也就是同一图像的不同分辨率 的子图集合。并且这些图像按照最大的放在底部,最小的放在顶部,看起来像一座金字塔,所以 称作图像金字塔。它是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度采样方式, 生成N个不同分辨率的图像。获得金字塔一般有两个步骤:
- 1.利用低通滤波器进行图像平滑
- 2.对平滑后的图像进行重采样
在采样时有两种方式:上采样和下采样
上采样是使分辨率逐渐变高,下采样是让分辨率逐渐降低。
下采样的方法是将原图所有的偶数行和列去掉,这样宽和长都变成了原来的一半,图像面积变为原来的1/4。
而对于上采样,则有两个步骤。一是将图像在每个方向扩大为原来的两倍,新增的行和列以0填充。
第二步是使用先前同样的内核(乘以4)与放大后的图像卷积,获得 “新增像素”的近似值。
下面的图片直观的展示了上采样和下采样:
上采样
 下采样
下采样
 注意要区别由上下采样产生的不同尺寸的图像序列和金字塔的区别。金字塔不仅进行了重采样,还进行了图像平滑。
注意要区别由上下采样产生的不同尺寸的图像序列和金字塔的区别。金字塔不仅进行了重采样,还进行了图像平滑。
在使用中有两类主要的金字塔:高斯金字塔和拉普拉斯金字塔。
- 高斯金字塔(Gaussian pyramid): 用来向下采样,主要的图像金字塔
- 拉普拉斯金字塔(Laplacian pyramid): 用来从金字塔低层图像重建上层未采样图像,在数字图像处理中也即是预测残差,可以对图像进行最大程度的还原,配合高斯金字塔一起使用。
两者的简要区别:高斯金字塔用来向下降采样图像,而拉普拉斯金字塔则用来从金字塔底层图像中向上采样重建一个图像。 要从金字塔第i层生成第i+1层(我们表示第i+1层为G_i+1),我们先要用高斯核对G_i进行卷积,然后删除所有偶数行和偶数列。当然新得到图像面积会变为源图像的四分之一。按上述过程对输入图像G_0执行操作就可产生出整个金字塔。
当图像向金字塔的上层移动时,尺寸和分辨率就降低。OpenCV中,从金字塔中上一级图像生成下一级图像的可以用PryDown()。而通过PryUp()将现有的图像在每个维度都放大两倍。
图像金字塔中的向上和向下采样分别通过OpenCV函数pyrUp()和pyrDown()实现。
这里的向下与向上采样,是对图像的尺寸而言的(和金字塔的方向相反),向上就是图像尺寸加倍,向下就是图像尺寸减半。而如果我们按金字塔方向来理解,金字塔向上图像其实在缩小,这样刚好是反过来了。
但需要注意的是,PryUp()和PryDown()不是互逆的,PryUp()不是降采样的逆操作。这种情况下,图像首先在每个维度上扩大为原来的两倍,新增的行(偶数行)以0填充。然后用指定的滤波器进行卷积(实际上是一个在每个维度都扩大为原来两倍的过滤器)去估计“丢失”像素的近似值。
PryDown()是一个会丢失信息的函数。为了恢复原来更高的分辨率的图像,我们要获得由降采样操作丢失的信息,这些数据就和拉普拉斯金字塔有关系了。
一、高斯金字塔
高斯金字塔是在Sift算子中提出来的概念,高斯金字塔并不是一个金字塔, 而是有很多组(Octave)金字塔构成,并且每组金字塔都包含若干层(Interval)。
1.原理与定义
在高斯金字塔中,同一尺寸的图像通过不同的高斯核进行不同程度的高斯平滑,这些影像构成一个八度(Octave),
而只对影像进行高斯平滑只会改变图像的清晰度,并不会改变图像的大小。因此只有高斯平滑并不能称作高斯金字塔。
还需要有一个下采样的过程,也就是使图片变小的过程。这样才能构成不同大小的图像,形成金字塔。同一幅图片
不同高斯平滑得到的一组大小相同、清晰度不同的图像(Interval)组成一个八度(Octave),多个八度的集合组成高斯金字塔。
如下图所示:
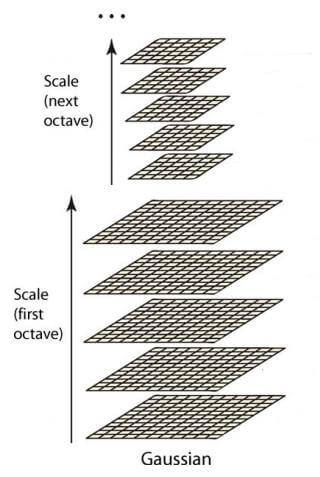
高斯金字塔是通过高斯平滑和亚采样获得一些列下采样图像,也就是说第K层高斯金字塔通过平滑、亚采样就可以获得K+1层高斯图像, 高斯金字塔包含了一系列低通滤波器,其截至频率从上一层到下一层是以因子2逐渐增加,所以高斯金字塔可以跨越很大的频率范围。 高斯金字塔从效果上看是对图片进行了缩小+模糊,这样做的目的又是什么呢?答案是高斯金字塔在模仿图像的不同尺度。 这个概念很容易理解,所谓尺度是指图像的不同大小。例如,同一幅画,我们站在1m之外和3m之外看到的内容是不同的。 这就是高斯金字塔模仿的过程。我们之前在图像处理的时候,只是关注图像的二维信息,并没有考虑过图像的尺度或者说 纵深。而高斯金字塔就是为了给图像增加第三维——纵深。这样做的好处是可以提取图像不同尺度的信息。如在很远地方观察 我们只需要辨别这是一个人,这就够了。而当我们走进之后,才需要判断这个人是谁,看到更多细节。不同尺度反映的信息是 不同的。可以理解为高斯金字塔越高层,其表达的信息即越概括和抽象。底层有最丰富的信息。
尺度空间
上面所说高斯金字塔为图像建立了尺度空间。在高斯金字塔中,又如何量化和实现呢?两个变量很重要:八度(o)和层数(s)。 这两个变量(o,s)共同构成了高斯金字塔的尺度空间。在同一个八度中,所有图像的大小是相等的,o控制着金字塔中图像 的尺度,或者直观地说是图片的大小。而要区分同一八度中的那些图像,就需要s。s控制着同一个八度中图像不同的模糊程度。 这样(o,s)就可以确定金字塔中唯一一幅影像了,其公式为:
\[\sigma =\sigma_{0}2^{o+\frac{s}{S}}\]s表示某个八度中某一图像的层数,S表示某个八度的层数,o表示第几个八度。 这里的sigma可以理解为表示图像尺度的变量。其实也就是高斯卷积函数中的一个变量,高斯卷积函数如下表示:
\[G(x,y)=\frac{1}{2\pi\sigma^{2}}e^{-\frac{(x-x_{0})^2+(y-y_{0})^2}{2\sigma^{2}}}\]对于参数sigma,在SIFT算子中固定值为1.6。
我们可以令:
\[k=2^{\frac{1}{S}}\]带入公式则有:
\[\sigma = \sigma_{0}2^{o}k^{s}\]sigma0表示图像的初始尺度。这里k只与每个八度中的层数有关。高斯金字塔中每个八度有S+3幅高斯图像,
而关于如何确定S,需要根据实际需求确定。所以每增加一级八度,o加1,所以sigma都要扩大2倍,在一个八度中k的上标s用来
区分不同的高斯核。
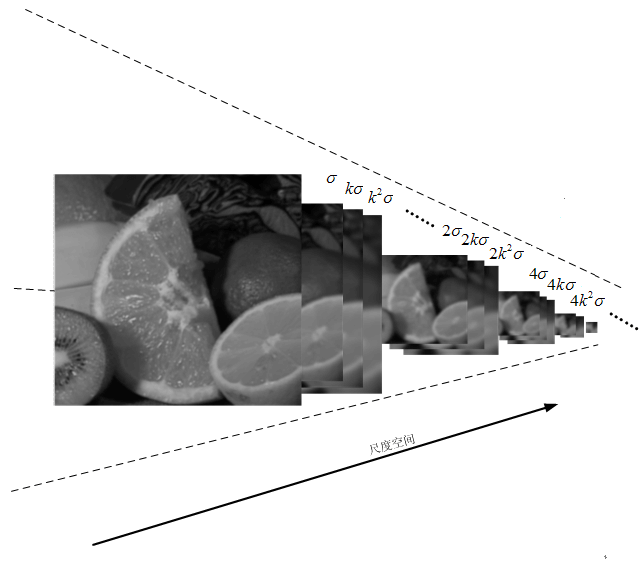 这样,我们令sigma0为δ,o和s都是从0开始。那么由上面的公式可以得到对于第一个八度依次有:
这样,我们令sigma0为δ,o和s都是从0开始。那么由上面的公式可以得到对于第一个八度依次有:
对于第二个八度,则o=1,s=1,所以有:
\[2\delta,2k^{2}\delta,2k^{3}\delta,2k^{4}\delta...\]从这里我们看到,尺度是在逐渐增加的。因为k是2的1/S次方,其值是恒大于1的。所以k的次方也是恒大于1的。 所以尺度的数值越大,表示的对应的图像就越小,表达的信息就越概括。
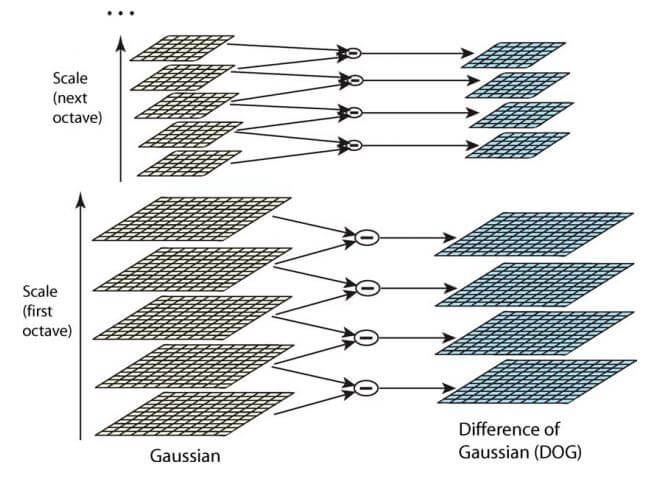
2.高斯差分金字塔(DOG)
构建高斯金字塔是为了后续构建差分高斯金字塔。对同一个八度的两幅相邻的图像做差得到插值图像,
所有八度的这些插值图像的集合,就构成了差分高斯金字塔。过程如下图所示,
差分高斯金字塔的好处是为后续的特征点的提取提供了方便。
 对于某一层,高斯函数G对图像I的模糊函数可表示如下:
对于某一层,高斯函数G对图像I的模糊函数可表示如下:
则高斯差分函数如下:
\[D(x,y,\sigma)\\=(D(x,y,k\sigma)-D(x,y,\sigma))\otimes I(x,y)\\=L(x,y,k\sigma)-L(x,y,\sigma)\]L(x,y,σ)表示某一层,所以这个公式就表示了上一层与下一层做差,即可得到DOG。
3.尺度空间连续性
前面我们说了,在高斯金字塔中,每个八度都有S+3幅影像。但是并没有解释为什么。这里我们介绍原因。
S表示的是在差分高斯金字塔(DOG)中求极值点的时候,我们
要在每个八度中求S层点。每一层极值点在三维空间
(图像二维,尺度一维)中比较获得。因此为了获得S层点,
那么差分高斯金字塔中应该要有S+2幅影像。而如果DOG中
有S+2幅影像,那么对应的高斯金字塔则应该有S+3幅影像。
因为DOG是由高斯金字塔相邻两层相减得到。至此,便解释了
为什么在高斯金字塔中每层要有S+3层影像。
但是还有一个问题,那就是为什么要在每个八度中求S层点。
这样做的目的是为了保持尺度的连续性。
通过高斯模糊函数和高斯差分函数,可以确定一个八度中(
如第一个八度)高斯图像和差分高斯图像的尺度如下:
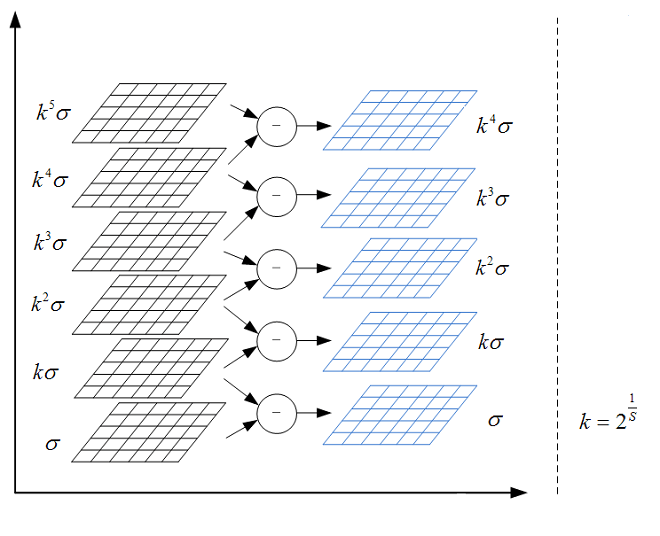 这里S=3,所以每个八度会有3+3=6幅图像。由之前的公式:
这里S=3,所以每个八度会有3+3=6幅图像。由之前的公式:
那么这里k等于2的1/3次方。将k依次带入计算出的尺度,有:
在当前八度中个高斯图像的尺度依次为:
当前八度中各差分高斯图像的尺度依次为:
\[\delta,2^{\frac{1}{3}}\delta,2^{\frac{2}{3}}\delta,2^{\frac{3}{3}}\delta,2^{\frac{4}{3}}\delta\]同时有之前的公式,我们可以推断出下一个八度中的高斯图像尺度为:
\[2\times \delta,2\times2^{\frac{1}{3}}\delta,2\times2^{\frac{2}{3}}\delta,2\times2^{\frac{3}{3}}\delta,2\times2^{\frac{4}{3}}\delta,2\times2^{\frac{5}{3}}\delta\]下一层的差分高斯图像尺度为:
\[2\times\delta,2\times2^{\frac{1}{3}}\delta,2\times2^{\frac{2}{3}}\delta,2\times2^{\frac{3}{3}}\delta,2\times2^{\frac{4}{3}}\delta\]而在高斯差分金字塔中,除去第一层和最后一层,中间三层是获得极值点 的层。换句话说就是只有在这些层上才发生了上下两层比较 获得极值点的操作。第一层和最后一层因为无法进行比较, 所以获得不了极值点。将能够获得极值点的高斯差分图像尺度 连在一起,那么有:
\[2^{\frac{1}{3}}\delta,2^{\frac{2}{3}}\delta,2^{\frac{3}{3}}\delta,2\times2^{\frac{1}{3}}\delta,2\times2^{\frac{2}{3}}\delta,2\times2^{\frac{3}{3}}\delta\]但可能这样还看不出什么变化规律,但如果将上式化简一下,则有:
\[2^{\frac{1}{3}}\delta,2^{\frac{2}{3}}\delta,2^{\frac{3}{3}}\delta,2^{\frac{4}{3}}\delta,2^{\frac{5}{3}}\delta,2^{\frac{6}{3}}\delta\]可以明显地看到,尺度数据是连续的。我们通过在每个八度中
多构造三幅高斯影像达到了尺度空间连续的效果。这样到好处
是在尺度空间的极值点确定过程中,我们不会漏掉任何一个
尺度上的极值点。
最后一个问题是下一个八度的第一幅图像如何确定。结论是
当前八度中的第一幅图像是通过前一个八度的倒数第三幅图像得到。
4.高斯金字塔构建步骤
- 1.先将原图像扩大一倍之后作为高斯金字塔的第1组第1层,将第1组第1层图像经高斯卷积(其实就是高斯平滑或称高斯滤波) 之后作为第1组金字塔的第2层。
- 2.将σ乘以一个比例系数k,等到一个新的平滑因子σ=k*σ,用它来平滑第1组第2层图像,结果图像作为第3层。
- 3.如此这般重复,最后得到L层图像,在同一组中,每一层图像的尺寸都是一样的,只是平滑系数不一样。 它们对应的平滑系数分别为:0,σ,kσ,k^2σ,k^3σ……k^(L-2)σ。
- 4.将第1组倒数第三层图像作比例因子为2的降采样,得到的图像作为第2组的第1层, 然后对第2组的第1层图像做平滑因子为σ的高斯平滑,得到第2组的第2层,就像步骤2中一样, 如此得到第2组的L层图像,同组内它们的尺寸是一样的,对应的平滑系数分别为:0,σ,kσ,k^2σ,k^3σ……k^(L-2)σ。 但是在尺寸方面第2组是第1组图像的一半。
这样反复执行,就可以得到一共O组,每组L层,共计O*L个图像,这些图像一起就构成了高斯金字塔。 在同一组内,不同层图像的尺寸是一样的,后一层图像的高斯平滑因子σ是前一层图像平滑因子的k倍; 在不同组内,后一组第一个图像是前一组倒数第三个图像的二分之一采样,图像大小是前一组的一半。
二、拉普拉斯金字塔
在上面我们说了,图像的上采样和下采样并不是完全可逆的过程,原因之一就是在于下采样时损失了很多原图的信息。 而拉普拉斯金字塔则可以解决这个问题。拉普拉斯金字塔的公式如下:
\[L_{i}=G_{i}-UP(G_{i+1})\otimes G_{5\times 5}\]其中,Gi表示第i层的图像。UP()操作时将原图中位置为(x,y)的像素映射到目标图像
的(2x+1,2y+1)的位置,即上采样。G5×5表示5×5的高斯卷积核。在OpenCV中cv2.pyrUp()
函数完成的便是减号后面的一系列操作。公式可以写成:
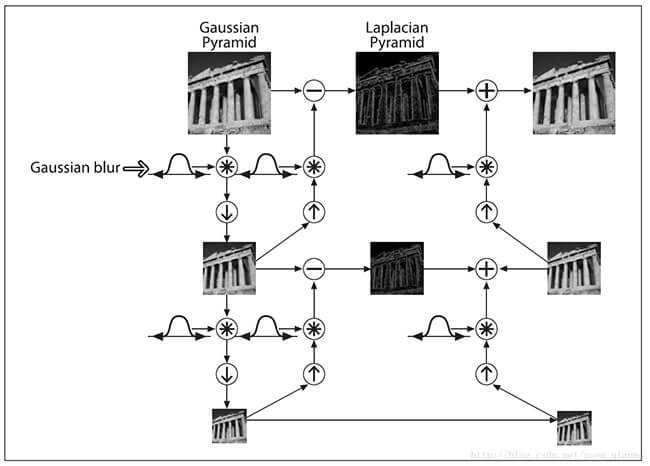
因此拉普拉斯金字塔是通过原图像减去缩小后再放大的图像而得到的图像构成的。
具体举例子如,首先将高斯金字塔中的第二层上采样,
然后再拿第一层减去第二层,这样得到拉普拉斯金字塔的第一层。同理将高斯金字塔的
第三层上采样,再与第二层做减法,得到拉普拉斯金字塔第二层。以此类推。
三、OpenCV实现
1.高斯金字塔
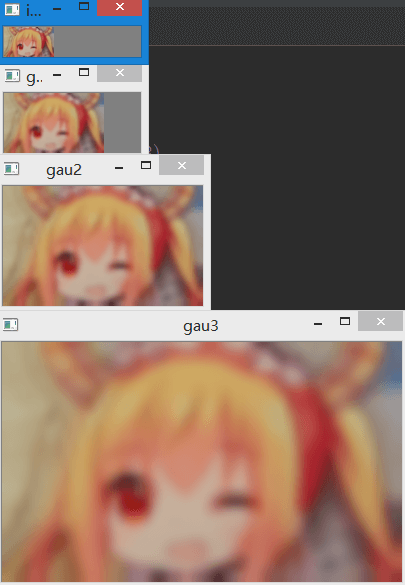
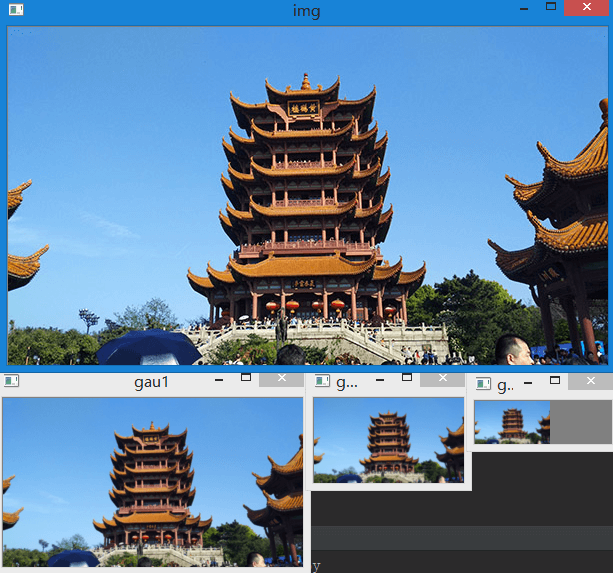
不管金字塔复杂的生成原理,在OpenCV中,实现高斯金字塔十分简单,只需要调用cv2.pyrDown()即可。
# coding=utf-8
import cv2
gauss0 = cv2.imread("E:\\600.jpg")
gauss1 = cv2.pyrDown(gauss0)
gauss2 = cv2.pyrDown(gauss1)
gauss3 = cv2.pyrDown(gauss2)
cv2.imshow("0", gauss0)
cv2.imshow("1", gauss1)
cv2.imshow("2", gauss2)
cv2.imshow("3", gauss3)
cv2.waitKey(0)
上述代码对img建了一个4层的高斯金字塔(包含原始图像),第0层为原始影像。可以看到图像的大小变化时非常快的。每一层都 缩小为原来的1/4。如对于一幅20000×20000的遥感影像来说,只需要建4层(包含原始影像)就可以使图像大小 变为2500×2500,而这比普通照片尺寸还要小,可以更方便地做相关处理了。

2.拉普拉斯金字塔
拉普拉斯金字塔在OpenCV中并没有直接的函数用于实现,但是由前面的计算公式,可以由高斯金字塔计算得来。
# coding=utf-8
import cv2
def getLplacian(gauss, g):
gauss_width = gauss.shape[0]
gauss_height = gauss.shape[1]
g_width = g.shape[0]
g_height = g.shape[1]
d_width = g_width - gauss_width
d_height = g_height - gauss_height
if d_width != 0 or d_height != 0:
temp = cv2.copyMakeBorder(gauss, d_width, 0, d_height, 0, cv2.BORDER_REPLICATE)
else:
temp = gauss
layer = cv2.subtract(temp, g)
return layer
gauss0 = cv2.imread("E:\\600.jpg")
# 首先生成高斯金字塔
gauss1 = cv2.pyrDown(gauss0)
gauss2 = cv2.pyrDown(gauss1)
gauss3 = cv2.pyrDown(gauss2)
# 然后利用上采样得到上一层图像
g2 = cv2.pyrUp(gauss3)
g1 = cv2.pyrUp(gauss2)
g0 = cv2.pyrUp(gauss1)
# 最后将对应层做差
# 注意对两个图像做差的时候,不要直接减,那会使用numpy的矩阵计算,
# 减出来的结果是不对的
l0 = getLplacian(gauss0, g0)
l1 = getLplacian(gauss1, g1)
l2 = getLplacian(gauss2, g2)
# 显示拉普拉斯金字塔
cv2.imshow("0", l0)
cv2.imshow("1", l1)
cv2.imshow("2", l2)
# 显示高斯金字塔
cv2.imshow("g0", gauss0)
cv2.imshow("g1", gauss1)
cv2.imshow("g2", gauss2)
cv2.waitKey(0)
上述代码基于4层的高斯金字塔构建了一个3层的拉普拉斯金字塔。看起来像是边界图,其中很多像素都是0。它常被用在图像压缩中。
(1)重采样图片大小问题
需要注意的是,在进行向上采样之后,原版代码在生成第三层拉普拉斯金字塔时总是报错如下。
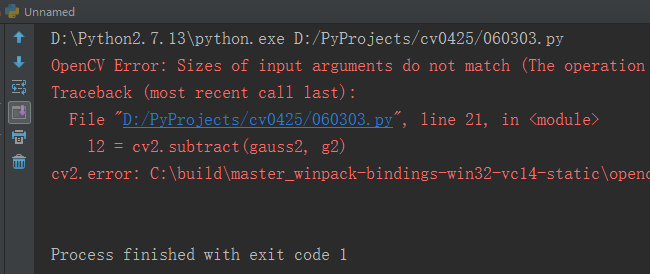 其中”Sizes of input arguments do not match”很关键,提示我们输入参数的规模不匹配。通过打印可以发现,
其中”Sizes of input arguments do not match”很关键,提示我们输入参数的规模不匹配。通过打印可以发现,
gauss2和g2的大小分别为(75, 150, 3)和(76, 150, 3)。图片大小不一致,所以无法相减。追根溯源,g2是由gauss3
上采样得到的,而gauss3是由gauss2下采样得到的。原图大小为300*600。金字塔各层大小如下所示:
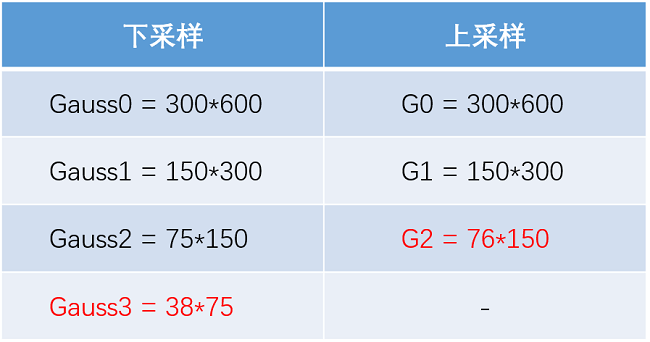 可以看到,问题出在由gauss2到gauss3这一步。因为75是奇数,除以2就是37.5,取整就是38。所以下一级的宽就是38了。
但是这就导致了上采样回去的时候38乘以2就变成了76,这就和75对不上了,所以就会出现问题。这就是这个问题的原因。
原因找到了,也就找到解决办法了。那就是在gauss2与g2相减之前,先对gauss2进行扩边,使其宽增加一个像素,问题
自然就可以解决了。这里用到了前面说过的扩边函数
可以看到,问题出在由gauss2到gauss3这一步。因为75是奇数,除以2就是37.5,取整就是38。所以下一级的宽就是38了。
但是这就导致了上采样回去的时候38乘以2就变成了76,这就和75对不上了,所以就会出现问题。这就是这个问题的原因。
原因找到了,也就找到解决办法了。那就是在gauss2与g2相减之前,先对gauss2进行扩边,使其宽增加一个像素,问题
自然就可以解决了。这里用到了前面说过的扩边函数cv2.copyMakeBorder()。注意之前四个方向扩展都是相同大小,但
可以设定只在一个方向进行扩边。在这里就是只在top扩展了1个像素,其它没修改。
其实再仔细研究就会发现,只要边长是奇数,让它重新上采样回来都会遇到这个问题。只不过如果不是要让上采样回来的图像
与原图做运算,这个问题都不大。如果要做运算,那么就要考虑扩边的问题。其实可以写成一个函数进行判断,如果边长不相等,
那么自动扩展成相等的,然后再进行运算。因为你无法知道到底会在什么地方出现奇数,什么时候该扩边。那么这个时候就需要用
函数来自动判断。如下函数是对OpenCV中减法的包装,保证大小相同后再做减法。而且仔细想想就会发现,如果出现边长不等问题,
那么原图的边长肯定是奇数,而且一定是重新上采样上来的图片比原图大。因为在下采样的时候为了变成正数,边长增加了0.5,
这样在上采样的时候再乘以2就是1。例如边长为1357,整个流程如下:
 可以看到,这个规律是固定的,那么代码就可以如下:
可以看到,这个规律是固定的,那么代码就可以如下:
def getLplacian(gauss, g):
gauss_width = gauss.shape[0]
gauss_height = gauss.shape[1]
g_width = g.shape[0]
g_height = g.shape[1]
d_width = g_width - gauss_width
d_height = g_height - gauss_height
if d_width != 0 or d_height != 0:
temp = cv2.copyMakeBorder(gauss, d_width, 0, d_height, 0, cv2.BORDER_REPLICATE)
else:
temp = gauss
layer = cv2.subtract(temp, g)
return layer
这样不管对于任何尺寸的图片,都可以很好地解决上采样回来之后无法与原图做运算的问题。
(2)图片减法问题
第二个需要注意的是这里的图像减法的这一步。我们可能想到很多种办法。
第一种是直接相减,第二种是利用OpenCV的加法,将第二个参数前面加个负号。
第三种是利用OpenCV的减法操作。
事实证明前两种方法都是有问题的。具体如下:
1.直接相减
不能直接相减,我们可以试试看l0 = gauss0 - g0,直接相减的结果如下。
 可以看到这与上面正确的结果相差是巨大的。这个问题在图像代数运算中也说过。那就是Numpy对图像是
按照矩阵来进行的。而图像的数据类型是uint8,没有负数。所以直接相减会导致出现负数,而一旦出现
负数就会“回滚”,也就是-1变成了最高的255。这也就是为什么图像中本应该是黑色的地方有这么多
白色的原因。
可以看到这与上面正确的结果相差是巨大的。这个问题在图像代数运算中也说过。那就是Numpy对图像是
按照矩阵来进行的。而图像的数据类型是uint8,没有负数。所以直接相减会导致出现负数,而一旦出现
负数就会“回滚”,也就是-1变成了最高的255。这也就是为什么图像中本应该是黑色的地方有这么多
白色的原因。
2.修改加法参数
将第二个参数前面加个负号,l0 = cv2.add(gauss0, -g0),结果如下:
 可以看到这与我们正确的结果非常类似,但是黑白是反过来的。这个我们之前也说过出现这种原因是和运算机制有关的。
OpenCV的加法是一种饱和操作。虽然结果类似,但是需要反色等操作,无法直接得到结果。
可以看到这与我们正确的结果非常类似,但是黑白是反过来的。这个我们之前也说过出现这种原因是和运算机制有关的。
OpenCV的加法是一种饱和操作。虽然结果类似,但是需要反色等操作,无法直接得到结果。
3.使用减法
在OpenCV中是有专门的减法的,函数是cvw.subtract()。还有一个相似的函数是cv2.absdiff()表示求两个矩阵差的绝对值。
这两者的区别在于,substract结果是有可能为负数的(设置的数据类型允许的情况下)。如果在这里设置的为uint8,那么当为
负数的时候,自动变为0。而absdiff则不同,他会对结果取绝对值,所以相比于subtract会有更多的非零像素展现出来。这些
非零像素其实就是相减以后值为负数的像素,只不过由于数据类型的限制,在前面没能显现出来。对比如下:
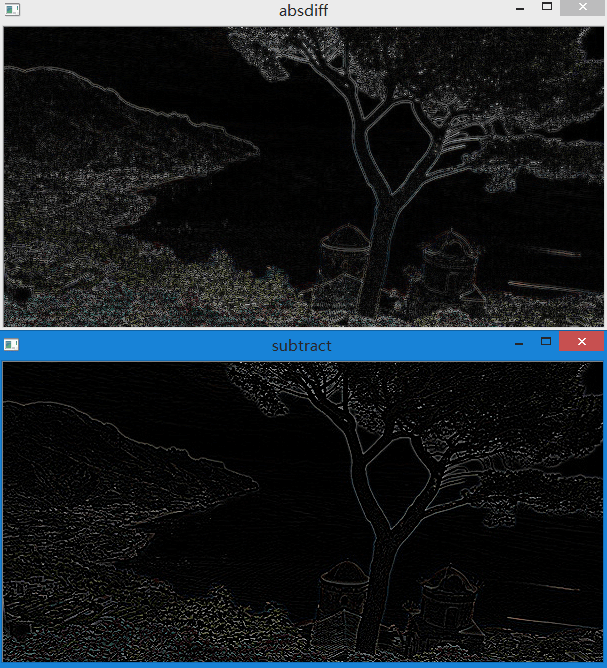 可以看到相比于absdiff,subtract的结果更为纯净。而至于到底用哪个,可能需要看具体的应用情况来决定。更多与图像代数运算
的内容可以看之前的这篇博客。
可以看到相比于absdiff,subtract的结果更为纯净。而至于到底用哪个,可能需要看具体的应用情况来决定。更多与图像代数运算
的内容可以看之前的这篇博客。
四、图像金字塔应用实例
金字塔的一个应用就是图像融合。例如在遥感影像中,如果某一幅影像某一区域效果不好,那么可以考虑拿其它数据源的同一片 区域的数据来“打补丁”,对图像进行缝合。但由于连接区域的像素不连续性,导致整体效果很差。这时金字塔就可以派上用场了。 可以实现视觉上的无缝缝合。这里使用OpenCV文档的例子,将一个桔子和苹果合成一个桔子苹果。融合的图像要保证大小相等。 金字塔影像融合步骤如下:
- 1.读入两幅图像
- 2.构建苹果和桔子的高斯金字塔
- 3.根据高斯金字塔计算拉普拉斯金字塔
- 4.在拉普拉斯金字塔的每一层进行图像融合
- 5.根据融合后的图像金字塔重建原始图像
融合代码如下:
# coding=utf-8
import numpy as np
import cv2
def getLplacianAdd(gauss, g):
gauss_width = gauss.shape[0]
gauss_height = gauss.shape[1]
g_width = g.shape[0]
g_height = g.shape[1]
d_width = g_width - gauss_width
d_height = g_height - gauss_height
if d_width != 0 or d_height != 0:
temp = cv2.copyMakeBorder(gauss, d_width, 0, d_height, 0, cv2.BORDER_REPLICATE)
else:
temp = gauss
layer = cv2.add(temp, g)
return layer
def getLplacianSub(gauss, g):
gauss_width = gauss.shape[0]
gauss_height = gauss.shape[1]
g_width = g.shape[0]
g_height = g.shape[1]
d_width = g_width - gauss_width
d_height = g_height - gauss_height
if d_width != 0 or d_height != 0:
temp = cv2.copyMakeBorder(gauss, d_width, 0, d_height, 0, cv2.BORDER_REPLICATE)
else:
temp = gauss
layer = cv2.subtract(temp, g)
return layer
# 注意,这里我们对图像进行裁剪,不能使用图像缩放resize。
# 因为我们在采样的过程中,根据我们的算法,是在top和left两个方向增加了数值
# 所以整体图像是像右下方移动的
# 所以我们需要把我们重采样过程中top和left方向上多加的像素给减掉
# 如果只是单纯的resize,会发现图片整体和原图虽然大小一致,
# 但是图片中物体的位置是移动了的
# 因此这个操作是图像裁剪,与我们重采样时扩边操作对应
# 而不是图像的缩放
def restoreXY(origin, present):
ori_row = origin.shape[0]
ori_col = origin.shape[1]
pre_row = present.shape[0]
pre_col = present.shape[1]
if ori_row != pre_row or ori_col != pre_col:
result = present[pre_row - ori_row:, pre_col - ori_col:]
else:
result = present
return result
apple = cv2.imread("E:\\apple.png")
orange = cv2.imread("E:\\orange.png")
gpL = 6
# 为苹果建立高斯金字塔,包括原图共7层
gpA = [apple]
for i in range(gpL):
g = cv2.pyrDown(gpA[i])
gpA.append(g)
# 为桔子建立高斯金字塔,包括原图共7层
gpO = [orange]
for i in range(gpL):
g = cv2.pyrDown(gpO[i])
gpO.append(g)
# 基于高斯金字塔建立苹果的拉普拉斯金字塔
# 注意这里在建完金字塔后,将金字塔的第一层
# 用高斯金字塔的倒数第二层(第五层)替代了
# 这样才能再后来重新上采样的时候还原原图
# 否则只靠拉普拉斯金字塔的信息上采样是无法
# 还原原图的,只会得到黑乎乎的图像
# 而之所以用第5层,是因为建拉普拉斯金字塔
# 只能从高斯金字塔的导数第二层建起,而
# 倒数第二层对应索引是5
# 当然其实还有一种方案,那就是不替代拉普拉斯金字塔
# 的第一层,而是在第一层的前面再加一层高斯
# 金字塔。这样得到的拉普拉斯金字塔一共是7层
# 包括一层高斯金字塔的最后一层和6层正常的拉普拉斯
# 金字塔。但这样可能会给后面的范围带来些麻烦,
# 而且多一层对于融合效果提升不大,所以这里不采用这个方法。
# 当然可能会好奇,为什么一定要用
# 高斯金字塔的最后一层。前面也说了,正是因为
# 需要恢复原图信息,必须要有原图,否则是无法还原
# 原图信息的。高斯金字塔包含原图信息。
lpA = []
for i in range(gpL, 0, -1):
l = getLplacianSub(gpA[i - 1], cv2.pyrUp(gpA[i]))
lpA.append(l)
lpA[0] = gpA[-2]
# 基于高斯金字塔建立桔子的拉普拉斯金字塔
# 同时注意拉普拉斯金字塔的第一层的替换
lpO = []
for i in range(gpL, 0, -1):
l = getLplacianSub(gpO[i - 1], cv2.pyrUp(gpO[i]))
lpO.append(l)
lpO[0] = gpO[-2]
# 对于每一层金字塔将两个图像各取一半合并
# 这里用到了Numpy的hstack函数,表示将两个矩阵合并到一起,注意不是加
# 其中h表示水平方向,v表示竖直方向
# 例如A为3*3,B为3*3,hstack合并后矩阵大小是3*6
lpAO = []
for i in range(gpL):
rows, cols, bpt = lpA[i].shape
lp = np.hstack((lpA[i][:, :cols / 2, :], lpO[i][:, cols / 2:, :]))
lpAO.append(lp)
# 逐步上采样重建金字塔
# 注意这里的迭代变量关系
# 这里是拉普拉斯金字塔第一层上采样到与第二层大小一致,
# 然后与现有的第二层相加,得到新的第二层
# 再将这个新的第二层上采样,和第三层相加
# 所以需要注意并不是拿老的第二层与第三层相加
# 否则是得不到正确结果的
gao = lpAO[0]
for i in range(gpL - 1):
gao = cv2.pyrUp(gao)
gao = getLplacianAdd(lpAO[i + 1], gao)
# 由于重采样回来后图像变大了,所以可以重新裁剪到原图大小
gao = restoreXY(apple, gao)
# 直接混合对比
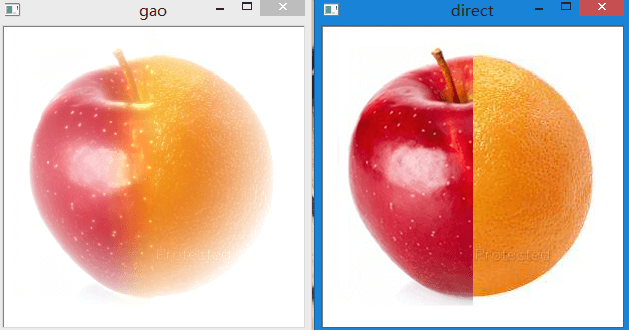
direct = np.hstack((apple[:, :apple.shape[1] / 2], orange[:, orange.shape[1] / 2:]))
cv2.imshow("gao" + gpL.__str__(), gao)
cv2.imshow("direct", direct)
cv2.waitKey(0)
最终的效果如下:
 OpenCV文档中的代码虽然看起来简单,但如果要真正运行起来还需要有很多修改。因为很多细节可能都没有体现出来。
只是为了简单演示,所以代码写的比较简单。但其实在这个过程中有很多问题和需要注意的地方。下面逐一说明:
OpenCV文档中的代码虽然看起来简单,但如果要真正运行起来还需要有很多修改。因为很多细节可能都没有体现出来。
只是为了简单演示,所以代码写的比较简单。但其实在这个过程中有很多问题和需要注意的地方。下面逐一说明:
1.图像重采样大小问题
这个问题在上面已经提到过了,由于采样过程中的取整,导致重采样后恢复的图片大小与原图不相同,导致不能和原图
进行运算。针对这个问题在代码中定义了getLplacianAdd和getLplacianSub两个函数专门用于保证大小一致。但是新的
问题也会出现。由于我们在函数中是通过扩边来保证大小一致的,所以导致扩边的大小会逐渐累积。在这个例子中有7层
高斯金字塔,累积量就已经很明显了。如下图是没有做处理之前的对比图,可以看到恢复的图像明显比原图大了。因此
我们还需要定义一个裁边的函数,用于将结果变成与原图大小一致。所以需要定义restoreXY函数。
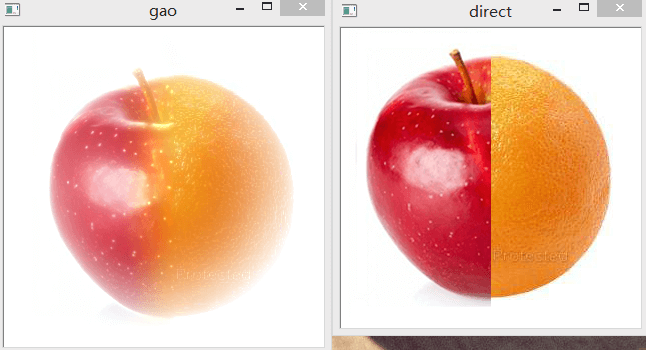 也正如注释里说的,不能将结果resize,而应该是裁边。因为我们处理的时候是扩边,两个操作是相对应的。
也正如注释里说的,不能将结果resize,而应该是裁边。因为我们处理的时候是扩边,两个操作是相对应的。
2.高斯金字塔的建立
在建立金字塔时,使用了一个gpL变量用于控制层数,这样后期可以十分方便修改金字塔的层数。同时在建立金字塔时,
使用了循环语句,而不再像之前一样一个个写了。建好的某一层放在一个list里。这里我们设置金字塔层数为6层,同时
把原始图像放进来作为第一层,所以一共是7层。建立好的金字塔如下所示:
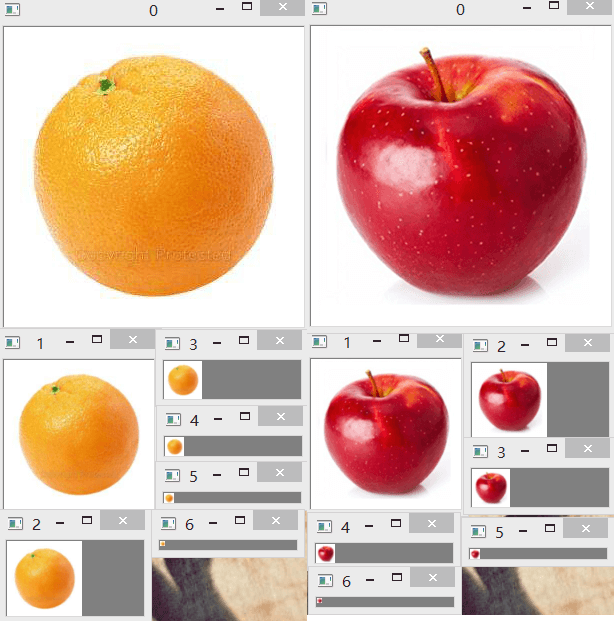
3.拉普拉斯金字塔建立
建立拉普拉斯金字塔也没有什么难度,正常建即可。高斯金字塔有7层,所以可以建6层拉普拉斯金字塔。 但有一点需要注意。由于我们是采用拉普拉斯金字塔进行图像融合。因此如果只建个金字塔是无法进行图像融合的。 利用拉普拉斯金字塔进行图像融合的原理是:首先对桔子和苹果分别建立拉普拉斯金字塔,然后将金字塔的每一层都 拼起来。合并之后,从金字塔的最顶层(图像最小的那一层)开始上采样,加到下一层上,然后再以运算后的结果为基础, 再上采样与下一层加。直到加完整个金字塔。这样图像的融合也就做好了。你可能会有以下疑惑:
(1)疑惑一
可能会奇怪,首先两个金字塔融合的时候也是直接拼起来的啊。并没有平滑过渡。为什么把整个金字塔加完就平滑了。 这里的关键是“上采样”。确实如果只是单纯加起来,完全不会产生平滑过渡的效果。但不要忘了,上采样其实是一个“平滑”的 过程,相当于把图像放大了。而这个放大的过程本身就在模糊图像。而且之前也见过拉普拉斯金字塔,很类似于图像边缘。 而且前面也说过在金字塔越高层(图像越小的层)其表达的特性就越抽象。所以在这里最小的层上面苹果和桔子的分界线是比较 清楚的,但是随着一层又一层的上采样,就越来越模糊了。
(2)疑惑二
金字塔黑乎乎的,为什么加起来就变成原图了。这也是问题的核心。这里所用的拉普拉斯金字塔不是真正的拉普拉斯
金字塔,或者说是经过“偷梁换柱”的拉普拉斯金字塔。原因在于我们建立完金字塔后,把金字塔的第0层给换成了高斯金字塔的
导数第二层。注意第0层。
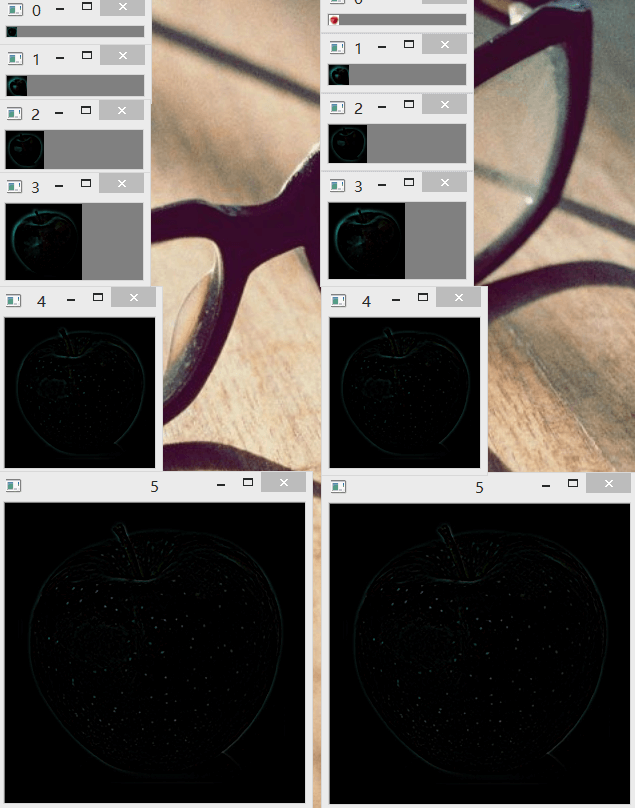 这里又有两个问题。为什么要换?以及为什么是倒数第二层?首先说为什么要换。这和我们的目的密切相关。因为
我们想通过金字塔进行图像融合。如果只是拉普拉斯金字塔,无论怎么重采样也是无法恢复成原图的。因为前面说过,拉普拉斯
金字塔保存的是高斯金字塔在降采样中损失的信息。靠损失的信息去恢复原图是不可能的。所以至少需要一层原图信息,基于此
再配上拉普拉斯金字塔,就可以弥补降采样时丢失的信息从而对原图进行还原。下图是没有原图信息还原出来的影像,一片黑。
这里又有两个问题。为什么要换?以及为什么是倒数第二层?首先说为什么要换。这和我们的目的密切相关。因为
我们想通过金字塔进行图像融合。如果只是拉普拉斯金字塔,无论怎么重采样也是无法恢复成原图的。因为前面说过,拉普拉斯
金字塔保存的是高斯金字塔在降采样中损失的信息。靠损失的信息去恢复原图是不可能的。所以至少需要一层原图信息,基于此
再配上拉普拉斯金字塔,就可以弥补降采样时丢失的信息从而对原图进行还原。下图是没有原图信息还原出来的影像,一片黑。
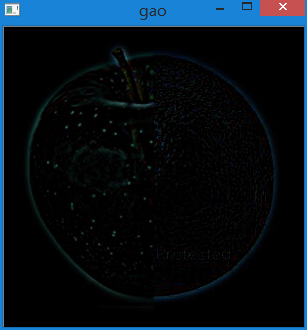 第二,为什么要把高斯金字塔的倒数第二层拿过来。
其实这很好理解。因为高斯金字塔一共7层。所以拉普拉斯金字塔最多能建6层。所以高斯金字塔的倒数第二层大小是与拉普拉斯
金字塔的最高一层(图像最小的一层)是相同的。这样便可以对两幅影像做代数运算。当然你也可以把高斯金字塔的倒数第一层加进来,
只不过这样的话,再进行运算前需要先对它上采样一下才行。下面分别是替换后的苹果、桔子的拉普拉斯金字塔。
第二,为什么要把高斯金字塔的倒数第二层拿过来。
其实这很好理解。因为高斯金字塔一共7层。所以拉普拉斯金字塔最多能建6层。所以高斯金字塔的倒数第二层大小是与拉普拉斯
金字塔的最高一层(图像最小的一层)是相同的。这样便可以对两幅影像做代数运算。当然你也可以把高斯金字塔的倒数第一层加进来,
只不过这样的话,再进行运算前需要先对它上采样一下才行。下面分别是替换后的苹果、桔子的拉普拉斯金字塔。

(3)疑惑三
既然可以加,而且核心是上采样,那为什么不用高斯金字塔。看了上面的描述,你会觉得,既然是上采样使图像进行了模糊。 那为什么不能直接拿高斯金字塔的最高层来做。答案是否定的。原因一因为上采样的模糊是针对整个图像的。把边界模糊了的同时也会把 其它轮廓一并模糊了。这显然不是我们想要的结果。我们只想要在交接处平滑。此外另一个原因是OpenCV的加法是饱和操作。这就 会带来一个问题。重新上采样上来的图像与该层相加很有可能像素值就超过255了,那么直接会被截成255。这样的直接结果就是导致 了整个图像越加颜色越淡(越白)。这也不是我们想要的结果。其实仔细观察利用拉普拉斯金字塔融合的结果。你同样会发现融合后的 图像比原图颜色淡了很多,也就是因为这个原因。而且金字塔的层数越多,颜色越淡。因为层数越多,加的次数越多。在后面还会 对不同层数的金字塔结果进行对比。说完了高斯金字塔不能的原因。那再来说说为什么拉普拉斯金字塔就不会出现越加越白或者说 相比于高斯金字塔好很多的结果呢?原因也很简单。因为高斯金字塔保存的是损失信息。从直观上来看,每一层基本都是黑的,也就是 说基本上像素都是0,正是因为像素基本都是0,所以这么多层加起来才不会像高斯金字塔一样变白。
(4)疑惑四
在前面介绍拉普拉斯金字塔生成的时候,说到了一个公式。如果把公式移项,便可得到如下表达形式,那么为什么不能用这个来还原呢?
\[G_{i}=L_{i}+PyrUp(G_{i+1})\]因为要注意代码中的算法和这里的公式有些不一样。这个公式是用于还原某一层的。而我们需要的是逐层是累加。 用这个公式还原的时候,并不会把上一层还原的结果作为下一层的输入。但我们需要的是把结果逐层累加,所以这个公式不适合。
建完以后的效果如下:
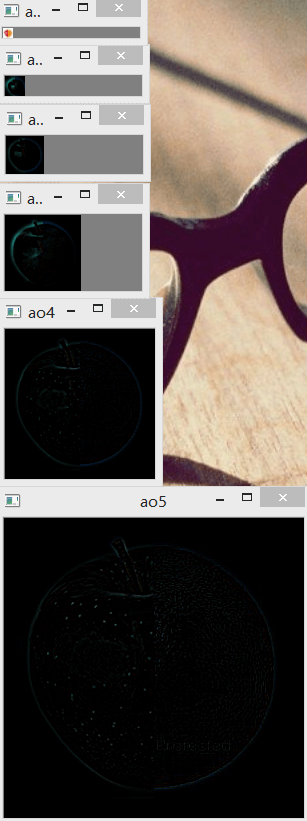
4.再谈图像代数运算
这是在对金字塔各层相加的时候想到的一个问题。觉得是初学者很容易走进的误区。一个简单的问题是,一张黑色的影像与一张白色
的影像相加,得到的影像是什么颜色的?
 可能我们会不假思索地回答,灰色的啊。这在日常生活中是没错的。但是在图像处理中就是
大错特错了。黑色是0,白色是255,两者相加还是255,所以还是白色的!那为什么我们会有黑+白=灰这样的常识呢?其实我们日常
生活中说的加,在图像处理中叫图像混合。所以在拉普拉斯金字塔中,图片上那些黑黑的地方,其实都是像素为0的地方,换句话说
都是透明的地方,这也就是为什么几层加在一起还是不会越界的原因。但如果进一步想,如果两个灰色的像素相加,像素值都是150,
那么相加的结果是300,假设图像数据类型是uint8,那么300超过255的范围,会被截取成255。这在直观的感受就是两个灰色的方块加
在一起变成了白色!
可能我们会不假思索地回答,灰色的啊。这在日常生活中是没错的。但是在图像处理中就是
大错特错了。黑色是0,白色是255,两者相加还是255,所以还是白色的!那为什么我们会有黑+白=灰这样的常识呢?其实我们日常
生活中说的加,在图像处理中叫图像混合。所以在拉普拉斯金字塔中,图片上那些黑黑的地方,其实都是像素为0的地方,换句话说
都是透明的地方,这也就是为什么几层加在一起还是不会越界的原因。但如果进一步想,如果两个灰色的像素相加,像素值都是150,
那么相加的结果是300,假设图像数据类型是uint8,那么300超过255的范围,会被截取成255。这在直观的感受就是两个灰色的方块加
在一起变成了白色!
5.不同层数金字塔影响
在上面我们说了,代码中使用了gpL来控制生成金字塔的层数。那么我们可以通过改变层数来观察不同层数对融合效果的影响,如下所示:
 可以看到,随着金字塔层数的不断增加,图像融合的效果也就越好。但同时也正如上面所说,层数越多,像素值越容易越界,从而白色
越多。因此可以合理地选择层数,从而达到融合效果与融合色彩的均衡。当然也可以通过对融合后的影像进行颜色处理,从而让它更好看。
可以看到,随着金字塔层数的不断增加,图像融合的效果也就越好。但同时也正如上面所说,层数越多,像素值越容易越界,从而白色
越多。因此可以合理地选择层数,从而达到融合效果与融合色彩的均衡。当然也可以通过对融合后的影像进行颜色处理,从而让它更好看。
6.图像压缩
其实这个图像融合的例子就是个图像压缩的过程,只不过在还原的时候用的方式不同。常规还原直接使用生成拉普拉斯金字塔的公式。 而这里是将还原结果不断累加。同时这里的原图信息是融合后的,如果只是单独桔子或苹果的信息,再配上拉普拉斯金字塔,就是压缩了。 金字塔对图片压缩的原理是通过对一幅图片建立高斯金字塔以及拉普拉斯金字塔,这样,我依据高斯金字塔的最顶层加上拉普拉斯金字塔, 就可以还原出原始图像。我们也只需要保存高斯金字塔顶部很小的一幅影像加上各层拉普拉斯金字塔的影像。而拉普拉斯金字塔保存的是 损失信息,各层之间的信息冗余较少,直观的反映是图片黑乎乎的,这样所占的空间是很小的。所以采用这种方式存储图像存储量会小很多。 下面是一个利用金字塔对图像压缩的例子,基于上面的代码修改而来。
# coding=utf-8
import cv2
def getLplacianAdd(gauss, g):
gauss_width = gauss.shape[0]
gauss_height = gauss.shape[1]
g_width = g.shape[0]
g_height = g.shape[1]
d_width = g_width - gauss_width
d_height = g_height - gauss_height
if d_width != 0 or d_height != 0:
temp = cv2.copyMakeBorder(gauss, d_width, 0, d_height, 0, cv2.BORDER_REPLICATE)
else:
temp = gauss
layer = cv2.add(temp, g)
return layer
def getLplacianSub(gauss, g):
gauss_width = gauss.shape[0]
gauss_height = gauss.shape[1]
g_width = g.shape[0]
g_height = g.shape[1]
d_width = g_width - gauss_width
d_height = g_height - gauss_height
if d_width != 0 or d_height != 0:
temp = cv2.copyMakeBorder(gauss, d_width, 0, d_height, 0, cv2.BORDER_REPLICATE)
else:
temp = gauss
layer = cv2.subtract(temp, g)
return layer
def restoreXY(origin, present):
ori_row = origin.shape[0]
ori_col = origin.shape[1]
pre_row = present.shape[0]
pre_col = present.shape[1]
if ori_row != pre_row or ori_col != pre_col:
result = present[pre_row - ori_row:, pre_col - ori_col:]
else:
result = present
return result
apple = cv2.imread("E:\\apple.png")
# 显示原图
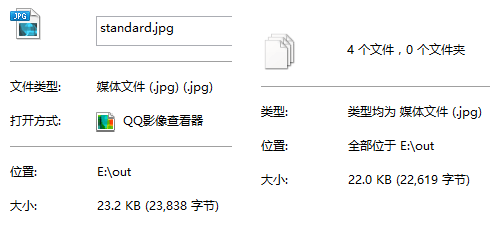
cv2.imshow("standard", apple)
# 将OpenCV读取的图像保存重新保存一下作为参照
# 注意不应该拿原始图像与经过OpenCV重新保存的图像比较大小
# 因为压缩算法,保存质量等原因会有很大差别
# 因此应该先将读取的图片保存一下作为参照
# 后续金字塔压缩的图片与这个图片比较大小
cv2.imwrite("E:\\out\\standard.jpg", apple)
# 建立金字塔的层数
gpL = 4
# 为读取的图像建立金字塔(gpL+1)层金字塔,其中第一层为原图
gpA = [apple]
for i in range(gpL):
g = cv2.pyrDown(gpA[i])
gpA.append(g)
# 根据建立的(gpL+1)层高斯金字塔生成gpL层拉普拉斯金字塔
# 同时为了后期能对图像进行还原,和融合一样,将第一层
# 用高斯金字塔的倒数第二层替换掉
lpA = []
for i in range(gpL, 0, -1):
l = getLplacianSub(gpA[i - 1], cv2.pyrUp(gpA[i]))
lpA.append(l)
lpA[0] = gpA[-2]
# 遍历金字塔,显示、输出各层图像
for i in range(gpL):
cv2.imshow(i.__str__(), lpA[i])
cv2.imwrite('E:\\out\\' + i.__str__() + '.jpg', lpA[i])
# 利用金字塔进行图像重建,测试效果
gao = lpA[0]
for i in range(gpL - 1):
gao = cv2.pyrUp(gao)
gao = getLplacianAdd(lpA[i + 1], gao)
# 修改因扩边操作增加的大小
gao = restoreXY(apple, gao)
# 显示利用金字塔恢复的图像
cv2.imshow("gao" + gpL.__str__(), gao)
cv2.waitKey(0)
保存的各层如下所示:
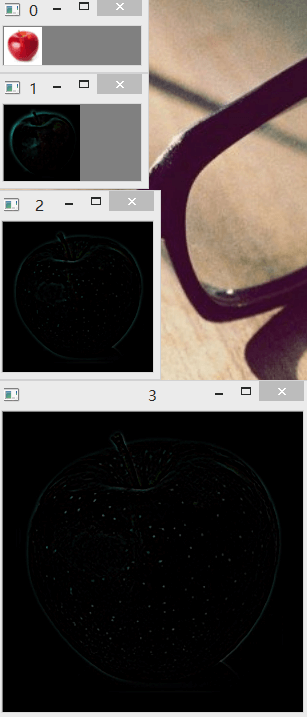 这和我们之前的结果是一样的,不同之处在于第0层影像融合的时候是融合后的影像,而这里只有一幅影像,所以直接就取高斯金字塔的倒数
第二层即可。同时利用金字塔还原的原图如下所示:
这和我们之前的结果是一样的,不同之处在于第0层影像融合的时候是融合后的影像,而这里只有一幅影像,所以直接就取高斯金字塔的倒数
第二层即可。同时利用金字塔还原的原图如下所示:
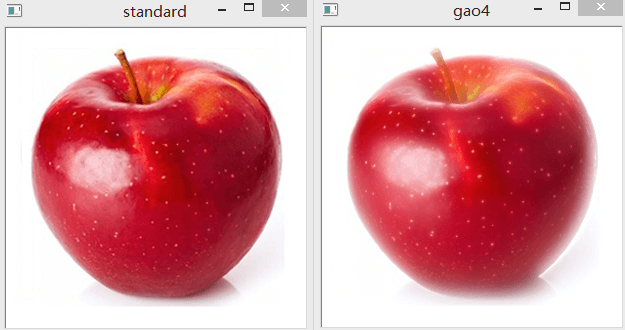 这里我们建了4层拉普拉斯金字塔,可以发现较好还原了原图,没有什么损失。在文件管理器中打开保存的路径,可以看到原始高斯金字塔的倒数第二层+拉普拉斯金字塔一共占用空间是22KB,而直接保存的大小是23.2KB。说明利用
金字塔进行压缩,节省了1.2KB的空间。由于原图本身就比较小,所以压缩的效果不明显。
这里我们建了4层拉普拉斯金字塔,可以发现较好还原了原图,没有什么损失。在文件管理器中打开保存的路径,可以看到原始高斯金字塔的倒数第二层+拉普拉斯金字塔一共占用空间是22KB,而直接保存的大小是23.2KB。说明利用
金字塔进行压缩,节省了1.2KB的空间。由于原图本身就比较小,所以压缩的效果不明显。

 同时,我们还可以研究统计不同金字塔层数对于压缩大小的影响,如下表所示。
同时,我们还可以研究统计不同金字塔层数对于压缩大小的影响,如下表所示。
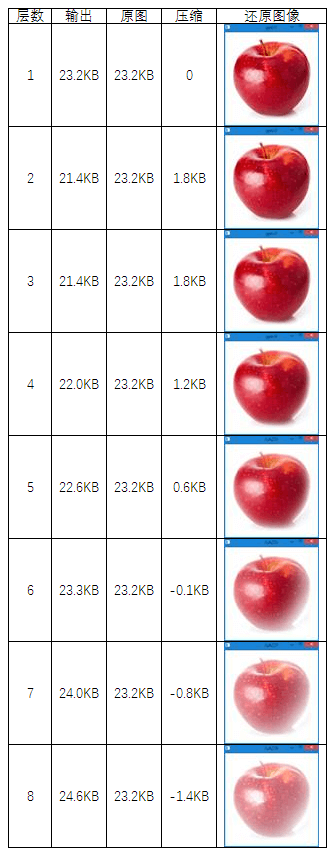 可以发现如下几条规律:
可以发现如下几条规律:
- 1.压缩率与金字塔层数有关系,但并不是层数越多压缩越多,而是有一个最佳的阈值。
- 2.与前面说过的一样,层数越多其颜色就越淡,恢复的效果就越差。
- 3.为了兼顾压缩和复原图像质量,应该根据图像合理选择金字塔层数。
盲目追求层数多,不仅压缩效果差,复原效果也差。
为了探究规律,我们用另一幅图片再次进行实验,得到如下结果:
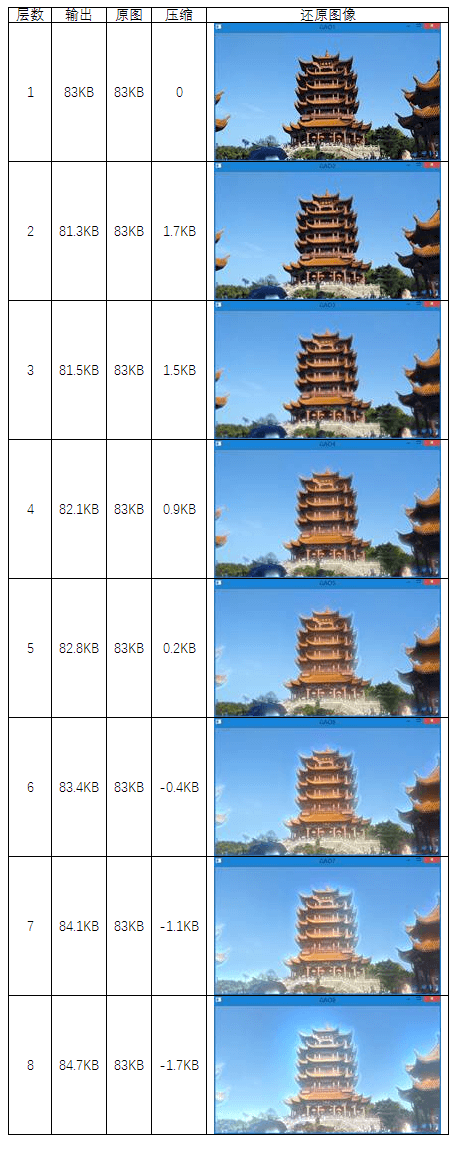 画出两幅图像压缩大小岁层数的变化关系如下图所示。
画出两幅图像压缩大小岁层数的变化关系如下图所示。
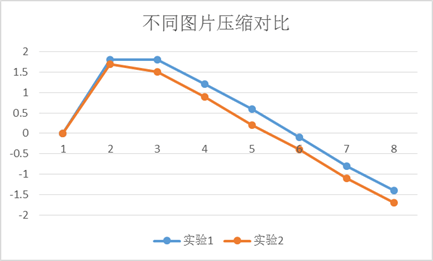 可以看到两幅图像有相同的规律,在2、3层时,压缩达到最大值。而且第一个实验的整体曲线在第二个实验上面。
至于到底是不是所有金字塔都是在2、3层达到最大压缩还有待考证。但从这两幅图片的结果来看,2层金字塔显然是最优的。
因为考虑到层数越多图像复原效果越差,所以层数越少越好。因此选择两层。
可以看到两幅图像有相同的规律,在2、3层时,压缩达到最大值。而且第一个实验的整体曲线在第二个实验上面。
至于到底是不是所有金字塔都是在2、3层达到最大压缩还有待考证。但从这两幅图片的结果来看,2层金字塔显然是最优的。
因为考虑到层数越多图像复原效果越差,所以层数越少越好。因此选择两层。
7.更多思考
相比于普通直接对图片进行压缩。金字塔压缩除了减少体积外,更重要的优势是可以提供多尺度图像。 从而可以减少不必要的资源浪费。如在浏览全局图时就没有必要将所有细节都加载。即先把基本的最小原图信息加载到内存, 然后根据用户浏览的尺度实时计算出当前区域对应的图像并显示。而如果没有金字塔,那么只要打开图像就会全图所有细节都会加载, 即使你只是为了看个缩略图。这对于计算机硬件内存,是个挑战,尤其当图像很大时。
这也就是为什么说打开一幅很大的图像要建影像金字塔的原因。如果不建金字塔,可能需要巨大的内存空间才能装载图像。 而建了之后,可以只装载高斯金字塔的最高层(最小的图像)到内存中。这样用户缩放到哪一级, 再依据拉普拉斯金字塔实时还原出该尺度下的图像。这也就是为什么ENVI打开遥感影像时会先建金字塔。 同时在浏览影像时会发现cpu占用率较高,而内存占用率相对稳定,无论不管放大或缩小图片。原因在于内存中只装载了最小的影像。 而放大的影像是依据拉普拉斯金字塔靠cpu实时算出来的。通过这种以“时间换空间”的方式降低了内存的占用。这种思想值得借鉴。 只需要建好高斯和拉普拉斯金字塔,并保留高斯的最高层(最小图片的那层)。这样就可以将原始影像还原到多尺度上。 可以很容易实现原始影像的放大和缩小。而这也就回归到了前面说的金字塔的最初目的,为图象提供了尺度空间。
至此,关于金字塔的这篇博客终于写完了。这也是我写了最长时间的一篇博客。前前后后花了大约10天时间。从原理、到实现, 发现了很多问题,也很有收获。
本文作者原创,未经许可不得转载,谢谢配合
