Menu
Random Explore

TensorFlow笔记6：MNIST 2

Jan 15,2018   14090 words   51 min

Tags: DeepLearning

在之前的博客中，通过将图像降维成一维矩阵，利用较简单的回归训练实现了MNIST，精度达到了90%。 但这个方法并不是最好的。很重要的一个原因就是降维损失了图像中重要的二维信息。 因此在MNIST的第二篇笔记中，通过卷积建立简单的学习网络，同时拥有更好的效果。 这里先贴出训练模型的代码，然后再分析。

一、模型训练代码

# coding= utf-8
import tensorflow as tf
import time


def weight_variable(shape, Name=None):
    # 截断正态分布（在-2u - 2u之间），更多可看函数的documentation
    # 这个函数用于返回一个指定shape的tensor，其中的数值符合正态分布
    # 模型中的权重在初始化时应该加入少量的噪声来打破对称性以及避免0梯度，因此标准差设为0.1
    # 注意这里的标准差初始值不能设置的太大，如2，否则会出现精度往复，无法提升的情况
    initial = tf.truncated_normal(shape, stddev=0.1)
    # 表示用初值创建一个TF变量并返回
    return tf.Variable(initial, name=Name)


def bias_variable(shape, Name=None):
    # 创建一个指定shape的常量tensor
    # 由于我们使用的是ReLU神经元，因此比较好的做法是用一个较小的正数来初始化偏置项
    # 以避免神经元节点输出恒为0的问题（dead neurons）
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial, name=Name)


def conv2d(x, W):
    # 卷积函数，x和W分别为输入图像和卷积核
    # 当选择padding为“SAME”时，边缘像素会被计算，周围补0
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding="SAME")


def max_pool_2x2(x):
    # 池化函数，表示选择2×2共4个像素中的最大值作为合并后的新像素值
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")


count = int(input("Specify train times:\n"))
nums = int(input("Specify number of images for every batch:\n"))
print("training...")

# 1.载入数据
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# 这里的x和y_分别表示每一张输入图像和其对应的标签
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
# 将输入的x向量变成28×28的图像
x_images = tf.reshape(x, [-1, 28, 28, 1])

# 第一层卷积
# 卷积大小为5×5，初始值随机且符合正态分布
# 输入通道数为1，卷积个数为32
W_conv1 = weight_variable([5, 5, 1, 32], Name='W_conv1')
b_conv1 = bias_variable([32], Name="b_conv1")
# 使用ReLU激活函数
h_conv1 = tf.nn.relu(conv2d(x_images, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

# 第二层卷积
W_conv2 = weight_variable([5, 5, 32, 64], Name='W_conv2')
b_conv2 = bias_variable([64], Name="b_conv2")

h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

# 全连接层
# 经过两层卷积，现在图像大小是7×7，且“厚度”为64
# 可以理解为对于第一层卷积后得到的14×14大小的图像用64个不同的卷积核进行卷积
# 最后得到64个7×7大小的卷积后的结果图像
# 而1024是人为指定的，表示全连接层有1024个神经元
# 全连接层的作用是把卷积输出的二维特征图转化成一维的一个向量
# 其实可以理解为有64*1024个7*7的卷积核卷积出来的
# 对于输入的每一张图，用了一个和图像一样大小的核卷积，这样整幅图就变成了一个数了
# 如果厚度是64就是那64个核卷积完了之后相加求和。这样就能把一张图高度浓缩成一个数了。
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])

# 下一步要进行矩阵相乘，因此这里reshape一下输入
# 可以理解为把所有卷积的结果全部变成一维线性的
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

# Dropout，防止过拟合
# Dropout就是在不同的训练过程中随机扔掉一部分神经元。
# 也就是让某个神经元的激活值以一定的概率p，让其停止工作，这次训练过程中不更新权值，也不参加神经网络的计算。
# 但是它的权重得保留下来（只是暂时不更新而已），因为下次样本输入时它可能又得工作了。
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

# 输出层
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

# 评价指标、模型的构建
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
saver = tf.train.Saver()

# 训练
# 写代码的时候，有时候会忘记写sess.close().我们可以使用系统的带的with来实现session的自动关闭
start = time.time()
with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)

    for i in range(count):
        batch = mnist.train.next_batch(nums)
        if i % 100 == 0:
            print("step", i, "accuracy", sess.run(accuracy, feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0}))
        sess.run(train_step, feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

    test_batch = mnist.train.next_batch(100)
    print("random test accuracy", sess.run(accuracy, feed_dict={x: test_batch[0], y_: test_batch[1], keep_prob: 1.0}))

    # 由于W维数过多，因此无法使用Numpy保存，会报错,因此使用TF的参数保存方法
    # 加载文件中的参数数据，会根据name加载数据并保存到变量W和b中
    saver.save(sess, './params.ckpt')
print("Parameters are saved.")
end = time.time()
print((end - start), "seconds in total.")

关于代码的详细解释可以看这个官方教程。这里对教程中没说到的一些地方简单说明。

1.截断正态分布

Normal Distribution称为正态分布，也称为高斯分布，Truncated Normal Distribution一般翻译为截断正态分布，也有称为截尾正态分布。

截断正态分布是截断分布(Truncated Distribution)的一种。截断分布是指，限制变量x取值范围(scope)的一种分布。 例如，限制x取值在0到50之间，即0<x<50。因此，根据限制条件的不同，截断分布可以分为：

  • 限制取值上限，例如，负无穷<x<50
  • 限制取值下限，例如，0<x<正无穷
  • 上限下限取值都限制，例如，0<x<50

正态分布则可视为不进行任何截断的截断正态分布，也即自变量的取值为负无穷到正无穷。

2.对于张量维度的理解

主要是抓住它的定义，如4维张量每一维的含义要分别弄清楚。这样虽然可能想象不出来它长什么样子，但知道代表什么意义。 第一维表示图像个数，第二三维表示图像宽高，第四维表示每一幅图像的色彩通道。 对于卷积核而言，4维每一维对应的意义又不同了。第一二维表示卷积核宽高，第三维表示输入(可以理解为需要做卷积的图像个数)，第四维表示卷积核个数(可以理解为需要输出的图像个数)。

3.激活函数

激活函数在上一篇博客已经做了很详细的介绍，这里就不再多说了。简而言之就是为了增加模型的表达能力，使其变成非线性模型。 可以参考这篇博客。

4.池化

在代码中采用了池化操作。池化的目的很简单，就是减小下一层图像的输入规模，合并相同信息。 池化层往往跟在卷积层后面。通过平均池化或者最大池化的方法将之前卷基层得到的特征图做一个聚合统计，达到降低数据量的目的。

因为图像具有一种“静态”属性，这也就是说在一个图像区域有用的特征极有可能在另一个区域同样适用。 例如，卷积层输出的特征图中两个相连的点的特征通常会很相似，没必要都保留作下一层的输入。 池化层可以将这些类似的信息做一个整合，输出红色这个特征。可以达到降低模型的规模，加速训练的目的。

最大池化就是取池化窗口内的最大值，平均池化就是取窗口内像素值的均值。

5.Dropout

它的目的是防止过拟合，一般用在全连接层。 Dropout就是在不同的训练过程中随机扔掉一部分神经元，类似于自然进化中的随机选择。 也就是让某个神经元的激活值以一定的概率p，让其停止工作，这次训练过程中不更新权值，也不参加神经网络的计算。 但是它的权重得保留下来（只是暂时不更新而已），因为下次样本输入时它可能又得工作了。示意图如下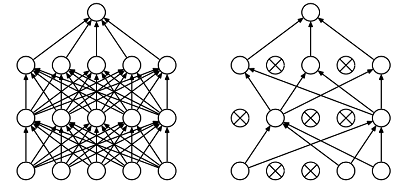： 更多信息可以参考这篇博客。

6.全连接层

在卷积神经网络的最后，往往会出现一两层全连接层，全连接一般会把卷积输出的二维特征图转化成一维的一个向量。 因为传统的网络我们的输出都是分类，也就是几个类别的概率甚至就是一个数–类别号，那么全连接层就是高度提纯的特征了，方便交给最后的分类器或者回归。

7.保存参数

利用TF的内置函数将模型的参数保存成文件，以便之后使用模型时直接调用。再次读取参数时，会根据保存参数的”name”属性将读取的参数赋给对应变量。

8.参数个数的确定

在第一层卷积中，指定输出特征为32，第二层为64，全连接层的神经元个数为1024。这些数字都是人为根据经验确定的，并没有什么“科学依据”。 参数个数一般为2的次方个。 需要注意的是，第二层的输入也就是第一层的输出。所以第二层卷积核的第三维是32，而不是1。

训练结果

为了观察不同训练次数对训练结果的影响，动用了各种电脑、服务器。分别训练了10000、20000、30000、50000和100000次。 也顺便测试了不同电脑的训练速度。

1.10000次

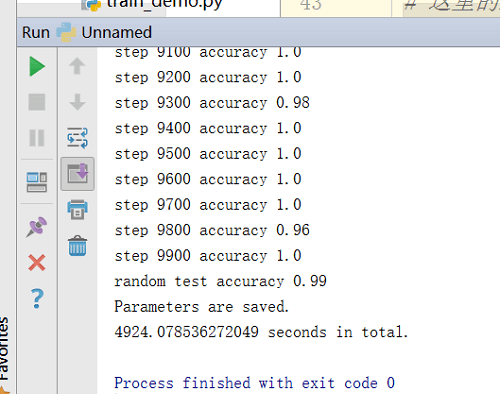
  • CPU:Intel Celeron N3450
  • 平均耗时:49.2s/百步
  • 随机测试精度:0.99
2.20000次

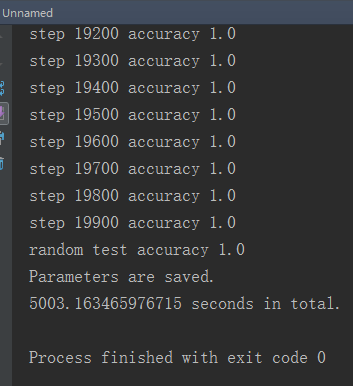
  • CPU:Intel Core i5 2430M
  • 平均耗时:50.03s/百步
  • 随机测试精度:1.0
3.30000次

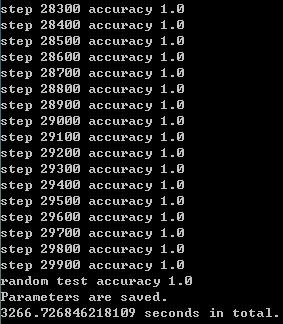
  • CPU:Intel Xeon X5670
  • 平均耗时:10.89s/百步
  • 随机测试精度:1.0
4.40000次

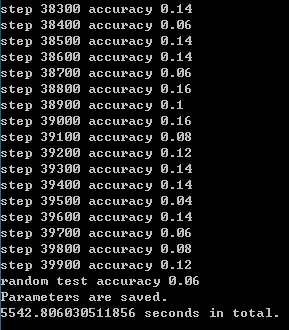
  • CPU:Intel Xeon X5670
  • 平均耗时:13.86s/百步
  • 随机测试精度:0.06
5.50000次

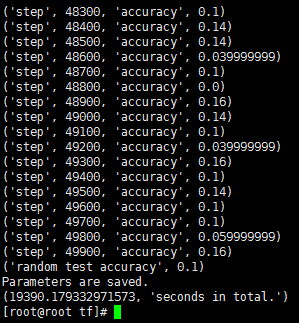
  • CPU:Intel Xeon E5-2682 v4
  • 平均耗时:38.78s/百步
  • 随机测试精度:0.1
6.100000次

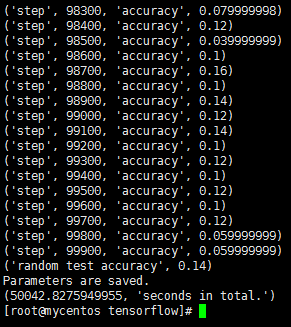
  • CPU:Intel Xeon E5-2630L v2
  • 平均耗时:50.04s/百步
  • 随机测试精度:0.14

可以发现在30000次之前，精度随着训练次数在逐渐提升，但之后，训练次数越多反而效果越差。 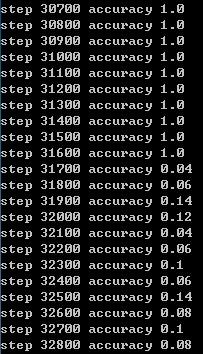通过查找，发现到31600步之后精度就突然下降了。初步判断可能是因为训练次数太多反而会干扰前面已经训练好的参数，造成混乱，导致精度下降，训练“过了”。 所以并不是训练次数越多越好。训练少了，精度不行，训练多了，精度可能也会下降。 同时也尝试在有GPU的笔记本上测试了一下，发现每百步大约是18秒左右，有GPU确实会快不少。

二、模型测试代码

# coding= utf-8
import tensorflow as tf


def weight_variable(shape, Name=None):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial, name=Name)


def bias_variable(shape, Name=None):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial, name=Name)


def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding="SAME")


def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")


count = int(input("Specify test times:\n"))
nums = int(input("Specify number of images for every test:\n"))

# 1.载入数据
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
x_images = tf.reshape(x, [-1, 28, 28, 1])

# 第一层卷积
W_conv1 = weight_variable([5, 5, 1, 32], Name='W_conv1')
b_conv1 = bias_variable([32], Name="b_conv1")
h_conv1 = tf.nn.relu(conv2d(x_images, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

# 第二层卷积
W_conv2 = weight_variable([5, 5, 32, 64], Name='W_conv2')
b_conv2 = bias_variable([64], Name="b_conv2")
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

# 全连接层
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

# 输出层
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1, W_fc2) + b_fc2)

# 评价指标、模型的构建
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
saver = tf.train.Saver()

accurs = []

# 测试
with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)
    # 加载文件中的参数数据
    saver.restore(sess, './params.ckpt')

    for i in range(count):
        batch = mnist.train.next_batch(nums)
        acc = sess.run(accuracy, feed_dict={x: batch[0], y_: batch[1]})
        accurs.append(acc)
        print("test", (i + 1), "accuracy", acc)
    print("final average accuracy", sum(accurs) / accurs.__len__())

如下，可以指定测试多少次，每次读取多少测试集中的数据。 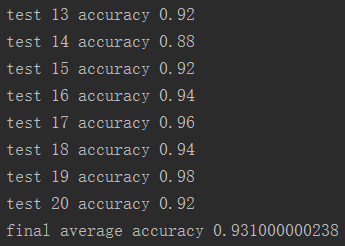如图，测试某次训练了600次的模型平均精度为0.93。

三、更一般的训练、测试代码

针对于上一个版本的代码将各层的参数写死了，这里将各层的参数独立出来，便于修改和调整。

1.训练代码

# coding= utf-8
import tensorflow as tf
import time


def weight_variable(shape, Name=None):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial, name=Name)


def bias_variable(shape, Name=None):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial, name=Name)


def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding="SAME")


def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")


# 网络相关参数
# 第一层卷积核个数
num_of_kernel_conv1 = 32
# 第二层卷积核个数
num_of_kernel_conv2 = 64
# 全连接层神经元个数
num_of_neu_fc = 2048

# 指定训练的次数以及每次训练随机抽样的图像个数
count = int(input("Specify train times:\n"))
nums = int(input("Specify number of images for every batch:\n"))
print("training...")

# 载入数据
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# 这里的x和y_分别表示每一张输入图像和其对应的标签
x = tf.placeholder(tf.float32, [None, 784])
y_ = tf.placeholder(tf.float32, [None, 10])
# 将输入的x向量变成28×28的图像
x_images = tf.reshape(x, [-1, 28, 28, 1])

# 第一层卷积
# 卷积大小为5×5，初始值随机且符合正态分布
# 输入通道数为1，卷积个数为num_of_kernel_conv1
W_conv1 = weight_variable([5, 5, 1, num_of_kernel_conv1], Name='W_conv1')
b_conv1 = bias_variable([num_of_kernel_conv1], Name="b_conv1")
# 使用ReLU激活函数
h_conv1 = tf.nn.relu(conv2d(x_images, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

# 第二层卷积
W_conv2 = weight_variable([5, 5, num_of_kernel_conv1, num_of_kernel_conv2], Name='W_conv2')
b_conv2 = bias_variable([num_of_kernel_conv2], Name="b_conv2")

h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

# 全连接层
# 经过两层卷积，现在图像大小是7×7，且“厚度”为num_of_kernel_conv2
# 可以理解为对于第一层卷积后得到的14×14大小的图像用num_of_kernel_conv2个不同的卷积核进行卷积
W_fc1 = weight_variable([7 * 7 * num_of_kernel_conv2, num_of_neu_fc])
b_fc1 = bias_variable([num_of_neu_fc])

# 下一步要进行矩阵相乘，因此这里reshape一下输入
# 可以理解为把所有卷积的结果全部变成一维线性的
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * num_of_kernel_conv2])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

# Dropout，防止过拟合
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

# 输出层
W_fc2 = weight_variable([num_of_neu_fc, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

# 评价指标、模型的构建
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
saver = tf.train.Saver()

# 训练
# 写代码的时候，有时候会忘记写sess.close().我们可以使用系统的带的with来实现session的自动关闭
start = time.time()
with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)

    for i in range(count):
        batch = mnist.train.next_batch(nums)
        if i % 100 == 0:
            print("step", i, "accuracy", sess.run(accuracy, feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0}))
        sess.run(train_step, feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

    test_batch = mnist.train.next_batch(100)
    print("random test accuracy", sess.run(accuracy, feed_dict={x: test_batch[0], y_: test_batch[1], keep_prob: 1.0}))

    # 由于W维数过多，因此无法使用Numpy保存，会报错,因此使用TF的参数保存方法
    # 加载文件中的参数数据，会根据name加载数据并保存到变量W和b中
    saver.save(sess, './params.ckpt')
print("Parameters are saved.")
end = time.time()
print((end - start), "seconds in total.")

通过修改全连接层的神经元个数，可以对比发现神经元数量越多，模型的精度提升越快。 例如下图是训练800次，每次随机抽样50张图像的训练过程和结果。

1024个神经元 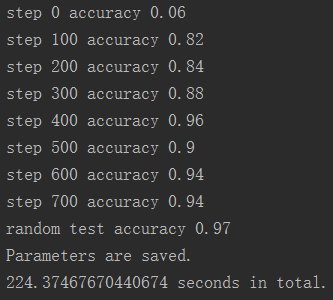2048个神经元 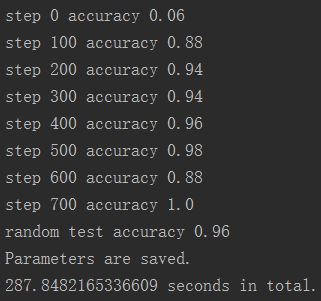可以发现有比较明显的差别，下面的训练精度提升较快。2048大约在200步时精度就到了0.9左右，而1024在400步才到0.9左右。 但尝试将第一层和第二层的卷积核个数翻倍，在有限次的训练下发现精度反而下降了。 可能是因为参数增加了很多，所以训练所需要的次数也增加了，训练更慢了。 但对于这个比较简单的网络，可能并没有必要设置那么多参数，这样不仅精度提升不明显，还会增加计算量，拖慢训练速度。 所以合理选择参数和训练次数对模型的最终结果影响很大。 就像上面说的，训练次数不一定越多越好，同理，参数个数也并不是越多越好。 而是要根据模型的需求和特点，不断调试，找到个较好的平衡点。

2.测试代码

相比于旧版的测试代码，主要针对模型参数做了修改，在测试前指定模型参数个数即可。 同时利用OpenCV实现了真实图片的测试。之前的测试都是在数据集上，这个代码可以实现实际图片的识别。

# coding=utf-8
import cv2
import tensorflow as tf
import numpy as np
from matplotlib import pyplot as plt
from tensorflow.contrib.learn.python.learn.datasets.mnist import read_data_sets


def weight_variable(shape, Name=None):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial, name=Name)


def bias_variable(shape, Name=None):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial, name=Name)


def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding="SAME")


def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")


# parameters for network
num_of_kernel_conv1 = 32
num_of_kernel_conv2 = 64
num_of_neu_fc = 2048

flag = input("Select mode:\n[1]Use your own image\n[2]Use test dataset\n")
if int(flag) is 1:
    path = input("Input image path:\n")
    # 读取图片测试，注意图片要求宽高相同
    input_image = cv2.imread(path, 0)
    input_image = cv2.resize(input_image, (28, 28), interpolation=cv2.INTER_AREA)
    input_image = np.float32(np.dot(input_image, 1.0 / 255.0))
    input_image = np.float32(np.abs(input_image - 1.0))
elif int(flag) is 2:
    image_index = int(input("Input image index:\n"))
    # 读入测试数据集测试
    mnist = read_data_sets("MNIST_data/", one_hot=True)
    images = mnist.test.images
    img = np.reshape(images[image_index], [1, 784])
    input_image = img.reshape(28, 28)
else:
    print("Invalid input.")

x_image = tf.reshape(input_image, [-1, 28, 28, 1])

# 第一层卷积
W_conv1 = weight_variable([5, 5, 1, num_of_kernel_conv1], Name='W_conv1')
b_conv1 = bias_variable([num_of_kernel_conv1], Name="b_conv1")
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

# 第二层卷积
W_conv2 = weight_variable([5, 5, num_of_kernel_conv1, num_of_kernel_conv2], Name='W_conv2')
b_conv2 = bias_variable([num_of_kernel_conv2], Name="b_conv2")
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

# 全连接层
W_fc1 = weight_variable([7 * 7 * num_of_kernel_conv2, num_of_neu_fc])
b_fc1 = bias_variable([num_of_neu_fc])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * num_of_kernel_conv2])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

# 输出层
W_fc2 = weight_variable([num_of_neu_fc, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1, W_fc2) + b_fc2)

# 评价指标、模型的构建
saver = tf.train.Saver()

# 测试
with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)
    # 加载文件中的参数数据
    saver.restore(sess, './params.ckpt')

    result = sess.run(y_conv)
    final = np.where(result[0] == max(result[0]))[0][0]
    print("final result:", final, "(", max(result[0]), ")")
    print("Probabilities:\n", result[0])

plt.imshow(input_image, cmap="gray")
plt.show()

运行代码后，输入1，选择”Use your own image”，再输入测试图片路径即可进行识别。 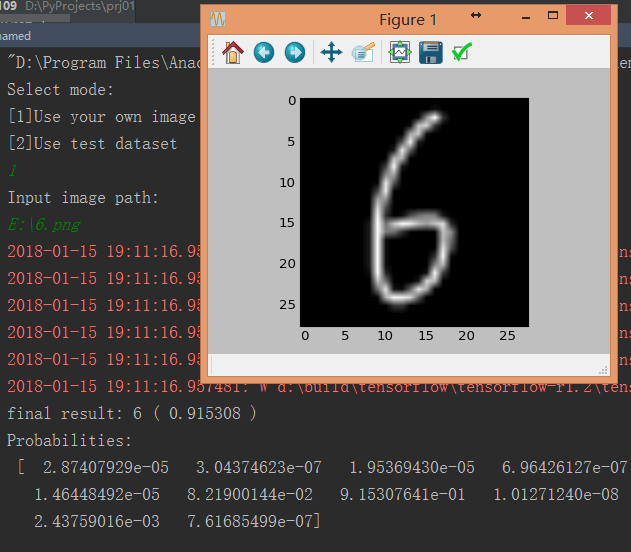如图比较准确地识别出了我写的”6”。但对于实际拍摄的照片，有时也会识别不出来。 识别精度远没有在测试数据集上的高。原因其实也很明显。 因为测试数据集和实际的照片还是有一定差距的，如果把实际照片处理成数据集的样子，识别率应该会提升。 这也说明了数据的重要性。

也可以输入”2”，对测试数据集中的图片进行测试，输入测试数据集中的图片索引。 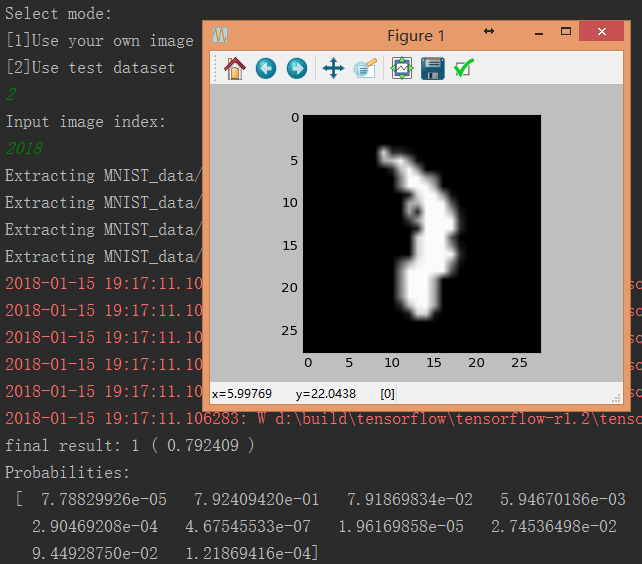这是一个我都没太认出来的”1”，图片索引是2018。

最后，顺带附上训练30000次后的模型参数文件，第一层卷积数是32，第二层是64，全连接层神经元个数是1024。 百度云链接：https://pan.baidu.com/s/1o9M1LME 密码：07nm

至此便完成了基于卷积网络的更复杂一点的MNIST模型，了解和熟悉了卷积网络的构建、训练和使用测试。

本文作者原创,未经许可不得转载,谢谢配合

返回顶部
鼓励一下