一、旋转与旋转矩阵
1.2D旋转
如下图所示,在坐标系O-xy中有一点P,已知坐标为(x,y),向量OP与X轴的夹角为β。将点P绕坐标原点O旋转了α角到P’。这里规定与右手系旋转方向相同的为旋转正方向,对于2D情况而言即逆时针旋转为旋转正方向。但在摄影测量中一般规定的是顺时针旋转方向为正方向。因此在应用时需要注意正方向的问题。正方向不同最终会导致的结果是旋转矩阵中sinα的符号是相反的。设P’点的坐标为(x’,y’)。点P、P’在x、y轴上的垂足分别为A、B、C、D。试用P点坐标表示P’点坐标。
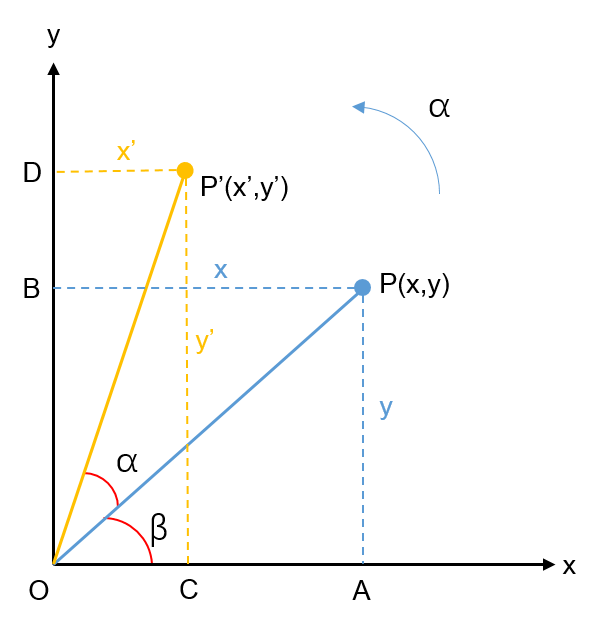
首先由于旋转,所以OP=OP’,设其长度为r。有如下公式。
\[r=\sqrt{x^{2}+y^{2}}\]而且,在三角形OPA中,有
\[\begin{matrix} cos\beta=\frac{x}{r} \\ sin\beta=\frac{y}{r} \end{matrix}\]也即
\[\begin{matrix} x=rcos\beta \\ y=rsin\beta \end{matrix}\]基于上面的已知条件,在三角形OP’C中,x’可以如下表示
\[\begin{matrix} x^{'}=r\cdot cos(\alpha+\beta)\\ =r\cdot (cos\alpha cos\beta-sin\alpha sin\beta)\\ =cos\alpha cos\beta\cdot r-sin\alpha sin\beta \cdot r\\ =cos\alpha \cdot x -sin\alpha \cdot y \end{matrix}\]同理y’如下
\[\begin{matrix} y^{'}=r\cdot sin(\alpha+\beta)\\ =r\cdot (sin\alpha cos\beta+cos\alpha sin\beta)\\ =sin\alpha cos\beta\cdot r+cos\alpha sin\beta \cdot r\\ =sin\alpha \cdot x +cos\alpha \cdot y \end{matrix}\]因此将上面的式子写成矩阵相乘的形式如下
\[\begin{pmatrix} x^{'}\\ y^{'} \end{pmatrix}=\begin{pmatrix} cos\alpha & -sin\alpha\\ sin\alpha & cos\alpha \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}\]这个公式便是二维平面内旋转前后的坐标关系。
2.3D旋转
在推得上面2D旋转的公式之后,3D旋转公式就相对简单了。例如某个点绕Z轴旋转α角,也就是说旋转后的Z坐标是不变的,变化的只是X、Y坐标。因此甚至可以基于2D公式,不用推导的写出下面这个式子,因为为了满足相等关系,必须补充系数矩阵元素。
\[\begin{pmatrix} x^{'}\\ y^{'}\\ z \end{pmatrix}=\begin{pmatrix} cos\alpha & -sin\alpha & 0\\ sin\alpha & cos\alpha & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x\\ y\\ z \end{pmatrix}\]而这个式子中的系数矩阵可以记为如下形式
\[R_{Z}(\alpha)=\begin{pmatrix} cos\alpha & -sin\alpha & 0\\ sin\alpha & cos\alpha & 0\\ 0 & 0 & 1 \end{pmatrix}\]便把R称为旋转矩阵。同时依据绕哪个轴旋转其坐标不变这个性质可以从形式上很快写出绕X、Y轴的旋转矩阵。但这里千万要注意并不是简单的把sin、cos挪个位置而已。因为涉及到旋转后的横、纵轴问题。例如以Y轴为转轴进行旋转,那么横轴应该是原坐标系的Z轴,纵轴应该是原坐标系的X轴。这一点一定要注意,否则会出错。也就是说最后的旋转矩阵中sin会相差一个负号,进而导致后续运算的出错。如下图。
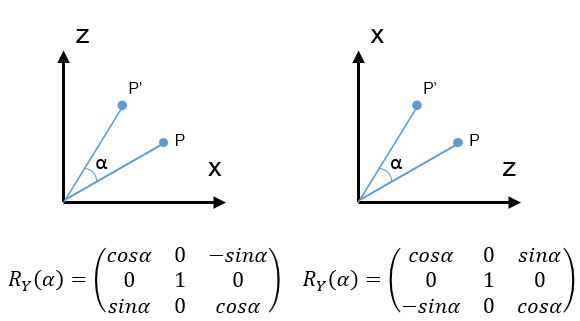
为了简单记住到底旋转后把谁当作横轴谁当作纵轴,总结了一个简单的小方法。即以哪个轴旋转,就用手握住这个轴,然后逆时针转动,最先碰到的那个轴作为横轴,剩下的那个作为纵轴,如下图。
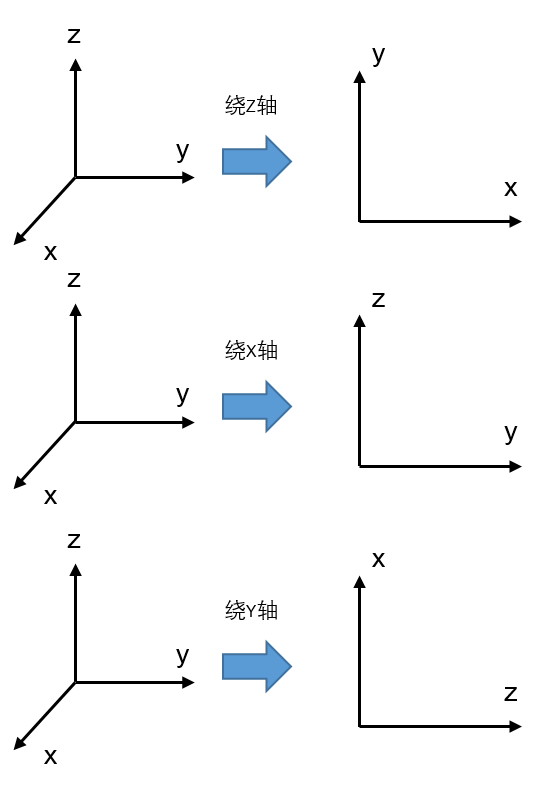
据此,可得到绕各轴旋转的旋转矩阵
\[\begin{matrix} R_{X}(\alpha)=\begin{pmatrix} 1 & 0 & 0\\ 0 & cos\alpha & -sin\alpha\\ 0 & sin\alpha & cos\alpha \end{pmatrix}\\ R_{Y}(\alpha)=\begin{pmatrix} cos\alpha & 0 & sin\alpha\\ 0 & 1 & 0\\ -sin\alpha & 0 & cos\alpha \end{pmatrix}\\ R_{Z}(\alpha)=\begin{pmatrix} cos\alpha & -sin\alpha & 0\\ sin\alpha & cos\alpha & 0\\ 0 & 0 & 1 \end{pmatrix} \end{matrix}\]二、欧拉角
欧拉角用于描述某个物体在坐标系中的姿态。假设一个物体的前方(朝向我们的方向)为X轴,右侧为Y轴,上方为Z轴。那么可以定义翻滚、俯仰和偏航如下。
翻滚,Roll,绕X轴

俯仰,Pitch,绕Y轴

偏航,Yaw,绕Z轴

这样对于任何一个姿态,我们可以利用Roll-Pitch-Yaw三个角依次旋转从而还原和表述物体的姿态了,形象而且直观。
但是这里有个很重要的问题,即绕谁旋转。每次是绕固定轴旋转还是绕旋转之后的轴旋转的,这会导致不一样的结果。也就是说 描述坐标系{B}相对于参考坐标系{A}的姿态有两种方式。
第一种是绕固定(参考)坐标轴旋转:假设开始两个坐标系重合,先将{B}绕{A}的X轴旋转γ,然后绕{A}的Y轴旋转β,最后绕{A}的Z轴旋转α,就能旋转到当前姿态。在整个过程中,坐标系{A}都没有发生变动。
另一种姿态描述方式是绕自身坐标轴旋转:假设开始两个坐标系重合,先将{B}绕自身的Z轴旋转α,然后绕Y轴旋转β,最后绕X轴旋转γ,就能旋转到当前姿态。
虽然两种旋转方式不同,但可以发现这两种描述方式得到的旋转矩阵是一样的,即绕固定坐标轴X-Y-Z旋转(γ,β,α)和绕自身坐标轴Z-Y-X旋转(α,β,γ)的最终结果一样,只是描述的方法有差别而已。
\[R = R_{Z}(\alpha)R_{Y}(\beta)R_{X}(\gamma)=\begin{pmatrix} cos\alpha cos\beta & cos\alpha sin\beta sin\gamma - sin\alpha cos\gamma & cos\alpha sin\beta cos\gamma + sin\alpha sin\gamma\\ sin\alpha cos\beta & cos\alpha cos\gamma + sin\alpha sin\beta sin\gamma & sin\alpha sin\beta cos\gamma - sin\gamma cos\alpha\\ -sin\beta & cos\beta sin\gamma & cos\beta cos\gamma \end{pmatrix}\]三、四元数
一个四元数的定义如下
\[\textbf{q}= q_{0}+q_{1}i+q_{2}j+q_{3}k\]一个四元数拥有一个实部和三个虚部,三个虚部之间满足如下关系。
\[\left\{\begin{matrix} i^{2}=j^{2}=k^{2}=-1\\ ij=k,ji=-k\\ jk=i,kj=-i\\ ki=j,ik=-j \end{matrix}\right.\]有时四元数也定义成(w,x,y,z)的形式,q0对应w,x、y、z依次对应q1、q2、q3。四元数的定义有了,那么如何用四元数表示旋转呢?如某次旋转是绕某一向量K=(Kx,Ky,Kz)进行了角度为θ的旋转,那么利用四元数就可以表示这个旋转:
\[\begin{matrix} x = K_{x}sin\frac{\theta}{2}\\ y = K_{y}sin\frac{\theta}{2}\\ z = K_{z}sin\frac{\theta}{2}\\ w = cos\frac{\theta}{2} \end{matrix}\]而且满足条件
\[x^{2}+y^{2}+z^{2}+w^{2}=1\]四、相互转换
1.四元数转旋转矩阵
设四元数为:
\[\textbf{q}= q_{0}+q_{1}i+q_{2}j+q_{3}k\]则其对应的旋转矩阵R为:
\[R=\begin{pmatrix} 1-2(q_{2}^{2}+q_{3}^{2}) & 2(q_{1}q_{2}-q_{0}q_{3}) & 2(q_{1}q_{3}+q_{0}q_{2})\\ 2(q_{1}q_{2}+q_{0}q_{3}) & 1-2(q_{1}^{2}+q_{3}^{2}) & 2(q_{2}q_{3}-q_{0}q_{1})\\ 2(q_{1}q_{3}-q_{0}q_{2}) & 2(q_{2}q_{3}+q_{0}q_{1}) & 1-2(q_{1}^{2}+q_{2}^{2}) \end{pmatrix}\]2.旋转矩阵转四元数
已知旋转矩阵如下
\[R=\begin{pmatrix} r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33} \end{pmatrix}\]其对应的四元数为
\[\left\{\begin{matrix} q_{0}=\frac{\sqrt{tr(R)+1}}{2}\\ q_{1}=\frac{r_{32}-r_{23}}{4q_{0}}\\ q_{2}=\frac{r_{13}-r_{31}}{4q_{0}}\\ q_{3}=\frac{r_{21}-r_{12}}{4q_{0}} \end{matrix}\right.\]其中tr(R)表示R矩阵的迹,也即矩阵R的主对角线(从左上方至右下方的对角线)上各个元素的总和。与旋转矩阵和四元数相互转换的内容,更详细可以参考这里。
3.欧拉角转旋转矩阵
某次旋转绕固定坐标轴X-Y-Z旋转(γ,β,α)或者说绕自身坐标轴Z-Y-X旋转(α,β,γ),对应的旋转矩阵如下
\[R = R_{Z}(\alpha)R_{Y}(\beta)R_{X}(\gamma)=\begin{pmatrix} cos\alpha cos\beta & cos\alpha sin\beta sin\gamma - sin\alpha cos\gamma & cos\alpha sin\beta cos\gamma + sin\alpha sin\gamma\\ sin\alpha cos\beta & cos\alpha cos\gamma + sin\alpha sin\beta sin\gamma & sin\alpha sin\beta cos\gamma - sin\gamma cos\alpha\\ -sin\beta & cos\beta sin\gamma & cos\beta cos\gamma \end{pmatrix}\]4.旋转矩阵转欧拉角
有旋转矩阵
\[R=\begin{pmatrix} r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33} \end{pmatrix}\]可求出各轴的旋转角为
\[\begin{matrix} \theta_{Z}= atan2(r_{21},r_{11})\\ \theta_{Y}= atan2(-r_{31},\sqrt{r_{31}^{2}+r_{33}^{2}})\\ \theta_{X}= atan2(r_{32},r_{33}) \end{matrix}\]atan2为C++中函数,atan2(y,x)的做法:当 x 的绝对值比 y 的绝对值大时使用 atan(y/x);反之使用 atan(x/y)。这样就保证了数值稳定性。需要注意的是,旋转顺序必须要是Z、Y、X。
5.欧拉角转四元素
将Z-Y-X欧拉角(或RPY角:绕固定坐标系的X-Y-Z依次旋转α,β,γ角)转换为四元数:
\[\textbf{q}=\begin{pmatrix} q_{0}\\ q_{1}\\ q_{2}\\ q_{3} \end{pmatrix}=\begin{pmatrix} cos(\frac{\alpha}{2})cos(\frac{\beta}{2})cos(\frac{\gamma}{2})+sin(\frac{\alpha}{2})sin(\frac{\beta}{2})sin(\frac{\gamma}{2})\\ sin(\frac{\alpha}{2})cos(\frac{\beta}{2})cos(\frac{\gamma}{2})-cos(\frac{\alpha}{2})sin(\frac{\beta}{2})sin(\frac{\gamma}{2})\\ cos(\frac{\alpha}{2})sin(\frac{\beta}{2})cos(\frac{\gamma}{2})+sin(\frac{\alpha}{2})cos(\frac{\beta}{2})sin(\frac{\gamma}{2})\\ cos(\frac{\alpha}{2})cos(\frac{\beta}{2})sin(\frac{\gamma}{2})-sin(\frac{\alpha}{2})sin(\frac{\beta}{2})cos(\frac{\gamma}{2}) \end{pmatrix}\]6.四元数转欧拉角
由四元数q=(q0,q1,q2,q3)或q=(w,x,y,z)到欧拉角的转换为
\[\alpha = arctan(\frac{2(q_{0}q_{1}+q_{2}q_{3})}{1-2(q_{1}^{2}+q_{2}^{2})})\\ \beta = arcsin(2(q_{0}q_{2}-q_{1}q_{3}))\\ \gamma = arctan(\frac{2(q_{0}q_{3}+q_{1}q_{2})}{1-2(q_{2}^{2}+q_{3}^{2})})\]由于arctan和arcsin的取值范围在−π/2 - π/2之间,只有180°,而绕某个轴旋转时范围是360°,因此要使用atan2函数代替arctan函数。
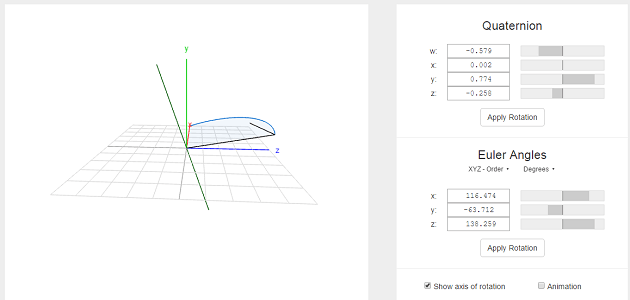
\[\alpha = atan2(2(q_{0}q_{1}+q_{2}q_{3}),1-2(q_{1}^{2}+q_{2}^{2}))\\ \beta = arcsin(2(q_{0}q_{2}-q_{1}q_{3}))\\ \gamma = atan2(2(q_{0}q_{3}+q_{1}q_{2}),1-2(q_{2}^{2}+q_{3}^{2}))\]最后这个网站(https://quaternions.online/) 可以动态展示四元数与欧拉角的对应关系和变化情况,便于理解。
五、参考资料
- https://blog.csdn.net/u012423865/article/details/78219787?locationNum=9&fps=1
- https://www.cnblogs.com/21207-iHome/p/6894128.html
- https://blog.csdn.net/csxiaoshui/article/details/65446125
- https://www.cnblogs.com/singlex/p/RotateMatrix2Euler.html
- https://blog.csdn.net/xuehuafeiwu123/article/details/74942989
本文作者原创,未经许可不得转载,谢谢配合
