本文主要从最小二乘理论、C++相关知识以及Ceres库使用三个方面来介绍。
一、最小二乘理论
1.最小二乘原理
最小二乘其实并不陌生,在很多地方都有用到。简单描述其思想就是,给定一堆观测数据:
\[x_{1},x_{2},x_{3}...,y_{1},y_{2},y_{3}...\]其中x与y具有某种对应关系。现在目的就是要根据这一堆观测的x、y值,找到最优的数学表述来表达它们之间的关系。 最小二乘原理就是将x带入估计的模型,可依次算出对应的估计的y值,然后将这些估计的y值与原始的观测值相减得到残差,并且最终的目的是让所有残差的平方和最小。 这时就认为达到最优了,其对应的模型就是要找的模型。这便是最小二乘拟合的思想。
从最小二乘的名字出发,“二乘”其实就是表示乘两遍,也就是对应上面的残差的平方。而“最小”表示是最小化所有残差的平方和。这便是最小二乘的核心思想了。这里需要注意的是,我们最小化的不是某一个残差,而是总体全部残差。
下面从数学角度描述一下非线性最小二乘以及相关名词。一个非线性最小二乘模型可以用下面的公式表述
\[\begin{split}\min_{\mathbf{x}} &\quad \frac{1}{2}\sum_{i} \rho_i\left(\left\|f_i\left(x_{i_1}, ... ,x_{i_k}\right)\right\|^2\right) \\ \text{s.t.} &\quad l_j \le x_j \le u_j\end{split}\]其中
\(\rho_i\left(\left\|f_i\left(x_{i_1},...,x_{i_k}\right)\right\|^2\right)\)
称为ResidualBlock,
\(f_i(\cdot)\)
称为CostFunction,它依赖于参数块(ParameterBlock)
\(\left[x_{i_1},... , x_{i_k}\right]\)
。在最优化问题中我们一般把多个自变量组成一个向量来处理。例如相机的位姿可以用平移向量加四元素来表示,一共7维。这个7维向量就称作参数块(ParameterBlock)。当然一个参数块也可以只包含一个变量。
\(l_{j},u_{j}\)
是变量
\(x_{j}\)
的上下限。
\(\rho_i\)
是一个LossFunction。它是一个用来减少离群点对非线性最小二乘优化问题影响的标量函数。特别的,当
\(\rho_i(x) = x\)
并且
\(l_j = -\infty,u_j = \infty\)
,那么这个模型就变成了更加熟悉的非线性最小二乘问题。
二、使用Ceres库之前需要具备的C++知识
在之前说了使用Ceres的步骤,在实际编写C++代码时,还会用到一些与Ceres无关、C++本身的特性。这里简单介绍一下,这样不至于后续看代码看不懂。
1.struct结构体构造函数
结构体也可以像类一样有构造函数,这样在新建一个结构体时,就对其进行了初始化。例如如下代码。
#include<iostream>
using namespace std;
//结构体定义结束后别忘了加封号
struct myStruct
{
double x_,y_;
//结构体的构造函数,传入x、y
myStruct(double x,double y)
{
x_=x;
y_=y;
}
};
int main()
{
//创建一个结构体的时候要写成指针形式,否则会报错
myStruct* s1 = new myStruct(3.4,6.1);
//注意指针形式的调用成员变量是箭头,不是点
cout<<s1->x_<<endl;
cout<<s1->y_<<endl;
return 0;
}
2.模板函数
C++中可以使用模板函数来减少代码的重复率。模板函数简单来说就是实现了一个函数多种使用。模板函数可以传入整形、浮点型、甚至字符型都可以,只需要更改模板类型即可。
#include<iostream>
using namespace std;
//模板函数定义的标准开头
template <typename T>
T add(T a,T b)
{
T sum = a+b;
return sum;
}
int main()
{
//注意模板函数调用的方式,需要在函数名后面用尖括号制定模板类型
double sum1 = add<double>(3.5,1.1);
double sum2 = add<int>(5,4);
string sum3 = add<string>("a","b");
cout<<"Typename double "<<sum1<<endl;
cout<<"Typename int "<<sum2<<endl;
cout<<"Typename string "<<sum3<<endl;
return 0;
}
3.const关键字
下面是一些使用const关键字的例子。
int b = 500;
const int* a = &b; [1]
int const *a = &b; [2]
int* const a = &b; [3]
const int* const a = &b; [4]
如果const位于星号左侧,则const就是用来修饰指针所指向的变量,即指针指向为常量;如果const位于星号的 右侧,const就是修饰指针本身,即指针本身是常量。因此,[1]和[2]的情况相同,都是指针所指向的内容为常量,这种情况下不允许对内容进行更改操作,如不能*a = 3;;[3]为指针本身是常量,而指针所指向的内容不是常量,这种情况下不能对指针本身进行更改操作,如a++是错误的;[4]为指针本身和指向的内容均为常量。
另外const的一些强大的功能在于它在函数声明中的应用。在一个函数声明中,const可以修饰函数的返回值,或某个参数;对于成员函数,还可以修饰是整个函数。一般放在函数体后,形如:
void fun() const
{
//your code here...
};
这种一般用于如果一个成员函数的不会修改数据成员,那么最好将其声明为const,因为const成员函数中不允许对数据成员进行修改,如果修改,编译器将报错,这大大提高了程序的健壮性。
4.运算符重载
在C++中用operator关键字重载运算符。运算符重载为类的成员函数的一般格式为:
<函数类型> operator <运算符>(<参数表>)
{
<函数体>
}
调用成员函数运算符的格式如下:
<对象名>.operator <运算符>(<参数>)
它等价于
<对象名><运算符><参数>
例如:a+b等价于a.operator +(b)。一般情况下,我们采用运算符的习惯表达方式。
当运算符重载为类的成员函数时,函数的参数个数比原来的操作数要少一个(后置单目运算符除外),这是因为成员函数用this指针隐式地访问了类的一个对象,它充当了运算符函数最左边的操作数。因此:
- (1) 双目运算符重载为类的成员函数时,函数只显式说明一个参数,该形参是运算符的右操作数。
- (2) 前置单目运算符重载为类的成员函数时,不需要显式说明参数,即函数没有形参。
- (3) 后置单目运算符重载为类的成员函数时,函数要带有一个整型形参。
下面是简单的示例。
#include<iostream>
using namespace std;
struct MyStruct
{
//声明一个结构体的成员变量
double x;
//结构体构造函数
MyStruct(double x_)
{
x = x_;
}
//在结构体中重载+运算符
//注意+左边的数字不需要显式指出,默认是在结构体中的成员变量
double operator+(double y)
{
return x*2+y*2;
}
};
int main()
{
//新建一个结构体,并以数字3初始化
MyStruct* my = new MyStruct(3);
//注意重载运算符的使用方式,这里my是结构体指针,因此使用箭头使用成员函数,不是点
double res = my->operator+(4);
//也可以利用星号将指针变成对象,这样就可以使用第二种调用方式了
double res2 = *my+6;
cout<<res<<endl;
cout<<res2<<endl;
return 0;
}
小括号重载用得最多的地方是“仿函数”。
5.仿函数
仿函数又称函数对象,它本质上是一种具有函数特质的对象,它 重载了operator()运算符,我们可以像使用函数一样使用该对象。通过重载()运算符,实现类似于函数的功能。下面是结构体中仿函数的简单示例。
#include<iostream>
using namespace std;
struct Functor
{
//在结构体中重载括号运算符,构造仿函数
bool operator()(double x, double y)
{
return x > y;
}
};
int main()
{
Functor* fun = new Functor();
//第一种使用方法,和重载运算符使用方法一样
cout<<fun->operator()(4.9,6.9)<<endl;
//第二种使用方法,建立一个临时变量
cout<<Functor()(6,4)<<endl;
return 0;
}
当然,结合上面的内容,我们可以写出一个更加复杂、健全的仿函数出来如下。
#include<iostream>
using namespace std;
struct Functor
{
//成员变量
double bias;
//构造函数
Functor(double b)
{
bias = b;
}
//模板仿函数
template <typename T>
bool operator()(const T &x, T &y) const
{
y = x + bias;
return true;
}
};
int main()
{
Functor* fun = new Functor(1.2);
double x=3.0,y;
fun->operator()<double>(x,y);
cout<<y<<endl;
return 0;
}
三、Ceres库的使用
1.Ceres库介绍
Ceres solver 是谷歌开发的一款用于非线性优化的库,在谷歌的开源激光雷达slam项目cartographer中被大量使用。使用Ceres库主要有以下几个步骤。
- 第一步,构建cost fuction(代价函数),也就是寻优的目标式,在优化问题中可以看作是目标函数
- 第二步,通过代价函数构建待求解的优化问题
- 第三步,配置求解器参数并求解问题
下面举例来说明,例如有函数
\[f(x)=\frac{1}{2}(10-x)^{2}\]求f(x)最小时对应的x。很明显,令f(x)的导数为0,对应的x即是要求的值。 但是如何把这个问题用最小二乘的思想来表示呢?这里其实我们使用了优化的思想。即我们对导数f’(x)求最小值,这其实就是最小二乘问题中对应的Cost Function(代价函数)。
又如,有如下函数模型
\[y = e^{mx + c}\]现有很多x、y观测值,需要对这个函数进行最小二乘拟合。和刚刚类似,我们需要去思考代价函数应该怎么写,也即当代价函数最大或最小时,刚好满足我们的需求。因为我们是对曲线进行拟合,自然希望拟合地越准确越好。“准确”这个概念用数学语言描述就是拟合得到的y’与真实的y的差值,其越小越好。
\[f_{cost} = y^{'}-y\]其中,y’是由我们估计出的参数算出来的估计值,y是观测值(真实值),它们的差值反映了估计的模型在该点的拟合准确度。 这里需要说明的是,由于后面在使用的时候是代价函数的平方,因此这里是y’-y还是y-y’并不会影响最终的结果。
当然,仅仅使某一个点的残差最小显然是不够的。从整体而言,我们希望所有点的差值都越小越好,而不是某一个点很好,其余都很差。 把这个思想转换成“代价函数”,那么就是所有残差之和最小。 也就是说,只要优化这个函数,就可以使所有残差和最小,从而在整体上做到对曲线的最佳拟合。
但是仔细想想这里会有个小问题。那就是残差不一定都是正的,例如某个点的残差是0.5,而另一个点是-0.5。显然这两个点的估计都是有误差的。但是把两个点的残差求和却为0,是最优的拟合。这显然和我们的认知有偏差。我们其实需要的只是残差的“大小”或者说“幅度”,至于其到底是正还是负我们并不关心。因为不管正负,都是误差。同时,在求某一点的残差时,不同相减顺序也会带来不同的结果,如10-5和5-10。因此我们需要寻找的这个总体的代价函数应该满足这两个条件:
- 1.不受残差相减顺序的影响
- 2.反映各残差之和,不受正负影响
基于以上两个条件,我们可以想到两种办法,一是对每一个残差都取绝对值,二是对每一个残差都取平方。使用哪一个方法更加简便呢?显然是取平方。因为取绝对值还涉及到一个逻辑判断,取平方直接数值运算就可以了。这也就是最小二乘名字中“二乘”的由来,就是为了解决以上两个问题。
所以我们总的优化目标函数就是各个代价函数之和。因为这里我们不考虑有粗差点,不用对离群点进行剔除,因此核函数系数为1,可以忽略了。
2.Ceres库编译配置
首先下载Ceres源码,可以点击这里下载或者去Github下载。下载完成后先安装其需要的依赖。注意这里的libcxsparese的版本问题,在你的电脑上可能会提示找不到对应版本,因为这些包本身也在不停变化着,所以可能你安装的时候已经过时了,最简单的办法就是让系统自己寻找最合适的版本,使用自动补全的办法。关于如何让apt命令自动补全可以看这篇博客。
# CMake
sudo apt-get install cmake
# google-glog + gflags
sudo apt-get install libgoogle-glog-dev libgtest-dev libgflags-dev
# BLAS & LAPACK
sudo apt-get install libatlas-base-dev liblapack-dev
# Eigen3
sudo apt-get install libeigen3-dev
# SuiteSparse and CXSparse (optional)
sudo apt-get install libsuitesparse-dev libcxsparse3.1.2
然后解压进入Ceres目录下,使用Cmake编译并安装。还是老样子,建议单独建一个build文件夹(当然如果不建也完全没问题,只是最后输出会clean一点)。至于要开几个线程同时编译,则根据实际情况了。再次提醒一下,这里cmake命令后两个点表示在上级目录搜索相关文件并生成,一个点表示在当前目录搜索相关cmake文件并生成。
mkdir build
cd build
cmake ..
make -j3
make install
如下图。
 这样,Ceres的环境就安装配置好了。
这样,Ceres的环境就安装配置好了。
3.Ceres库实现曲线拟合
最后,利用Ceres简单实现最小二乘曲线拟合。首先需要生成数据,这里采用OpenCV的随机数生成器生成误差。CmakeLists文件如下。
cmake_minimum_required(VERSION 2.6)
project(ceres_test)
set( CMAKE_CXX_FLAGS "-std=c++11 -O3" )
# 添加cmake模块以使用ceres库
list( APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake_modules )
# 寻找Ceres库并添加它的头文件
find_package( Ceres REQUIRED )
include_directories( ${CERES_INCLUDE_DIRS} )
# OpenCV
find_package( OpenCV REQUIRED )
include_directories( ${OpenCV_DIRS} )
add_executable(ceres_test main.cpp)
# 与Ceres和OpenCV链接
target_link_libraries( ceres_test ${CERES_LIBRARIES} ${OpenCV_LIBS} )
install(TARGETS ceres_test RUNTIME DESTINATION bin)
生成数据及拟合代码如下。
#include <iostream>
#include <opencv2/core/core.hpp>
#include <ceres/ceres.h>
using namespace std;
using namespace cv;
using namespace ceres;
//vector,用于存放x、y的观测数据
//待估计函数为y=3.5x^3+1.6x^2+0.3x+7.8
vector<double> xs;
vector<double> ys;
//定义CostFunctor结构体用于描述代价函数
struct CostFunctor{
double x_guan,y_guan;
//构造函数,用已知的x、y数据对其赋值
CostFunctor(double x,double y)
{
x_guan = x;
y_guan = y;
}
//重载括号运算符,两个参数分别是估计的参数和由该参数计算得到的残差
//注意这里的const,一个都不能省略,否则就会报错
template <typename T>
bool operator()(const T* const params,T* residual)const
{
residual[0]=y_guan-(params[0]*x_guan*x_guan*x_guan+params[1]*x_guan*x_guan+params[2]*x_guan+params[3]);
return true;
}
};
//生成实验数据
void generateData()
{
RNG rng;
double w_sigma = 1.0;
for(int i=0;i<100;i++)
{
double x = i;
double y = 3.5*x*x*x+1.6*x*x+0.3*x+7.8;
xs.push_back(x);
ys.push_back(y+rng.gaussian(w_sigma));
}
for(int i=0;i<xs.size();i++)
{
cout<<"x:"<<xs[i]<<" y:"<<ys[i]<<endl;
}
}
//简单描述我们优化的目的就是为了使我们估计参数算出的y'和实际观测的y的差值之和最小
//所以代价函数(CostFunction)就是y'-y,其对应每一组观测值与估计值的残差。
//由于我们优化的是残差之和,因此需要把代价函数全部加起来,使这个函数最小,而不是单独的使某一个残差最小
//默认情况下,我们认为各组的残差是等权的,也就是核函数系数为1。
//但有时可能会出现粗差等情况,有可能不等权,但这里不考虑。
//这个求和以后的函数便是我们优化的目标函数
//通过不断调整我们的参数值,使这个目标函数最终达到最小,即认为优化完成
int main(int argc, char **argv) {
generateData();
//创建一个长度为4的double数组用于存放参数
double params[4]={1.0};
//第一步,创建Problem对象,并对每一组观测数据添加ResidualBlock
//由于每一组观测点都会得到一个残差,而我们的目的是最小化所有残差的和
//所以采用for循环依次把每个残差都添加进来
Problem problem;
for(int i=0;i<xs.size();i++)
{
//利用我们之前写的结构体、仿函数,创建代价函数对象,注意初始化的方式
//尖括号中的参数分别为误差类型,输出维度(因变量个数),输入维度(待估计参数的个数)
CostFunction* cost_function = new AutoDiffCostFunction<CostFunctor,1,4>(new CostFunctor(xs[i],ys[i]));
//三个参数分别为代价函数、核函数和待估参数
problem.AddResidualBlock(cost_function,NULL,params);
}
//第二步,配置Solver
Solver::Options options;
//配置增量方程的解法
options.linear_solver_type=ceres::DENSE_QR;
//是否输出到cout
options.minimizer_progress_to_stdout=true;
//第三步,创建Summary对象用于输出迭代结果
Solver::Summary summary;
//第四步,执行求解
Solve(options,&problem,&summary);
//第五步,输出求解结果
cout<<summary.BriefReport()<<endl;
cout<<"p0:"<<params[0]<<endl;
cout<<"p1:"<<params[1]<<endl;
cout<<"p2:"<<params[2]<<endl;
cout<<"p3:"<<params[3]<<endl;
return 0;
}
运行结果如下,和我们之前给定的参数对比发现精度还是不错的。
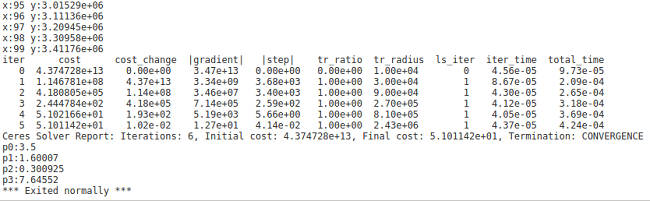
四、参考资料
- https://www.ceres-solver.org/nnls_tutorial.html
- https://www.ceres-solver.org/nnls_modeling.html#introduction
- https://blog.csdn.net/cqrtxwd/article/details/78956227
- https://www.ceres-solver.org/installation.html
- https://blog.csdn.net/clozxy/article/details/5679887
- https://zhidao.baidu.com/question/526327349.html
本文作者原创,未经许可不得转载,谢谢配合
