一、李群李代数原理
1.群(Group)
说到李群，从字面上便知道它是满足某些特殊条件的“群”，是群的一种。那么什么是群？群是数学上的一个概念。简单而言，群(Group)是一种集合加上一种运算的代数结构。一般把集合记作\(A\)，运算记作\(\cdot\)。群要求这个运算满足以下几个条件：
- 封闭性
- 结合律
- 幺元
- 逆
这里简单知道这些性质即可。如果想更深入了解，可以百度相关内容。群结构保证了在群上的运算具有良好的性质。
2.李群
上面说了群的概念，自然而然地，李群是一种特殊的群。特殊在李群是指具有连续(光滑)性质的群。这里说的连续就是我们理解的意思，不是离散的，如整数群。这便是李群的概念了。只要一个集合加一种运算能构成群，并且这个群还是连续光滑的，那么这个群就是李群。
3.特殊正交群SO(n)与特殊欧式群SE(n)
三维旋转矩阵构成了特殊正交群SO(3)，变换矩阵构成了特殊欧式群SE(3)。同理对于二维就是SO(2)、SE(2)。那么它们是不是李群呢？答案是肯定的。因为我们能够直观想象一个刚体在三维、二维空间中连续运动，因此它们是连续的。而由李群定义，连续的群就可以被称为李群。所以它们也是李群。
4.对旋转矩阵求导
首先回顾一下旋转矩阵的性质，旋转矩阵是正交阵，也即矩阵的逆等于矩阵的转置。因此，对于任意一个旋转矩阵R，下面这个式子都是成立的。
\[RR^T=RR^{-1}=I\]考虑R代表某个相机的旋转，它随时间连续变化，即为时间的函数\(R(t)\)。每一时刻它依然是旋转矩阵，因此对于t时刻而言，上面的式子依然成立。
\[R(t)R(t)^T=I\]方程两遍对时间求导，有：
\[\dot{R}(t)R(t)^T+R(t)\dot{R}(t)^T=0\]把R和R的转置看成两个不同的变量，这就满足uv的求导法则了(u’v+uv’)。I为单位阵与时间无关，对时间求导后为0。
将第二项移到等式右边，有
\[\dot{R}(t)R(t)^T=-R(t)\dot{R}(t)^T\]又根据矩阵转置法则
\[(AB)^T=B^TA^T,(A^T)^T=A\]所以
\[\dot{R}(t)R(t)^T=-R(t)\dot{R}(t)^T=-(\dot{R}(t)R(t)^T)^T\]仔细观察等式两边，如果令\(\dot{R}(t)R(t)^T=A\)，那么简写成下面这个形式
\[A=-A^T=>A^T=-A\]如果熟悉反对称矩阵便知道，这便是反对称矩阵的定义。满足上述条件的A则称为反对称矩阵。因此\(\dot{R}(t)R(t)^T\)是一个反对称矩阵。而在之前说过，对于任意一个反对称矩阵都能找到一个与之对应的向量。
\[\dot{R}(t)R(t)^T=[\phi(t)]_X\]这里\(\phi(t)\)为向量，\([\phi(t)]_X\)表示取该向量对应的反对称矩阵，公式见这篇博客。
现在我们的目的是看看对旋转矩阵R求导是什么结果，所以对上式等式两边右乘R(t)。由正交阵性质(转置等于逆)，有
\[\dot{R}(t)=[\phi(t)]_XR(t)= \begin{pmatrix} 0 & -\phi_{3} & \phi_{2}\\ \phi_{3} & 0 & -\phi_{1}\\ -\phi_{2} & \phi_{1} & 0 \end{pmatrix}R(t)\]因此可以看到，对旋转矩阵R(t)求导，其结果就等于该时刻对应的旋转向量\(\phi(t)\)的反对称矩阵与其本身R(t)的乘积。
如果令\(t_0=0\)，且此时旋转矩阵为\(R(0)=I\)，按照导数定义，可以把R(t)在0附近一阶泰勒展开：
\[\begin{matrix} R(t)\approx R(t_0)+\dot{R}(t_0)(t-t_0)\\ =R(0)+[\phi(0)]_XR(0)(t-0)\\ =I+[\phi(0)]_X(t) \end{matrix}\]可以看出\(\phi\)反映了R的导数性质，所以称它在SO(3)原点附近的正切空间上。同时在t0附近，让\(\phi\)保持常数\(\phi(t_0)=\phi_0\)。
\[\dot{R}(t)=[\phi(t_0)]_XR(t)=[\phi_0]_XR(t)\]这是一个关于R的微分方程，且初值\(R(0)=I\)。所以
\[R(t)=exp([\phi_0]_Xt)\]这个式子表明了旋转矩阵与另一个反对称矩阵通过指数关系发生了联系。当我们知道某时刻的旋转矩阵时，即存在一个向量\(\phi\)满足上述关系。
5.李代数
每个李群都有与之对应的李代数，李代数描述了李群的局部性质。李代数由一个集合V，一个数域F和一个二元运算[,]组成。其中二元运算被称为李括号，表达了两个元素的差异。它不要求结合律，而要求元素和自己做李括号以后为0的性质。例如，对于三维向量的叉积可以看成是一种李括号(因为向量和其本身做叉积结果为0)。
在之前说的\(\phi\)就是一种李代数。SO(3)对应的李代数是定义在三维空间的向量，记为\(\phi\)，每个\(\phi\)都可以生成一个反对称矩阵。对于SE(3)，其李代数可以看成是一个6维向量，前三维为平移，后三维为旋转。
对于SO(3)李代数实际上就是由所谓的旋转向量组成的空间，而指数映射则是罗德里格斯公式。通过它们，可以把SO(3)李代数中的任意一个向量对应到位于SO(3)中的旋转矩阵。但一般为了方便，直接采用矩阵迹的性质计算旋转轴旋转角来获得旋转向量的方式。
对于李群和李代数而言，指数映射完成了它们的联系。旋转矩阵的导数可以由旋转向量指定，指导着如何在旋转矩阵中进行微积分运算。但指数映射只是一个满射。这就是说，对于每个李群中的元素，都可以找到一个李代数元素与之对应，但可能存在多个李代数中的元素对应到同一个李群中的元素。例如旋转0度和转360度结果都是一样的，具有周期性。但如果把旋转角度限定在正负180以内，那么李群与李代数是一一对应的。它们之间的关系如下图所示。
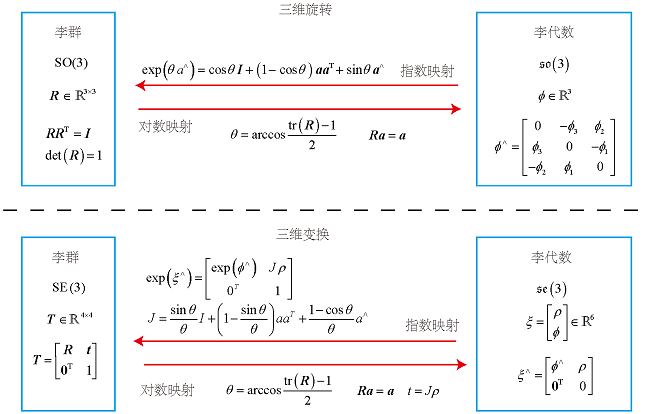
二、Sophus库
1.Sophus库安装
Sophus库也是一个Cmake的库，不过无需安装(安装也可以)。首先从Github上面下载源代码。
git clone https://github.com/strasdat/Sophus.git
cd Sophus
git checkout a621ff
这里使用的是非模板类的Sophus。所以才指定了提交版本。如果使用最新的模板类的Sophus也可以，但是代码会有点变化。
然后按照Cmake工程的流程操作即可。
mkdir build
cd build
cmake ..
完成后如下。
然后直接make命令生成即可。
这样就可以直接使用了。这个库就编译到了你当前文件夹下。但貌似这样以后在IDE中使用Sophus库的话会提示找不到这个库，但编译、运行都是没问题的，只是不会出现代码提示，如下所示。
有点不爽。因此如果你也遇到这种情况，可以这样做。首先回到build文件夹下，运行命令make install，完成后如下。
这样，上面的这个问题便能解决了。
安装之后建议保留源文件，否则可能会给后续使用带来麻烦。
2.Sophus库使用
(1)Cmakelist和文件包含写法
Cmake文件中应该这样写
# 为使用 sophus，您需要使用find_package命令找到它
find_package( Sophus REQUIRED )
include_directories( ${Sophus_INCLUDE_DIRS} )
add_executable(useSophus useSophus.cpp)
target_link_libraries(useSophus ${Sophus_LIBRARIES} )
同时要注意，Sophus必须要C++11才能正确编译。如果出现类似错误，加上下面这句话即可。
set(CMAKE_CXX_STANDARD 11)
在我的电脑上即使make install也找不到Sophus库，还不知道原因。所以我是这样写的。
add_executable(useSophus useSophus.cpp)
target_link_libraries(useSophus Sophus)
由于CMake找不到库，所以find_package也就可以不写了，写了也没用。或者说必须得删掉，否则CMake检查都通不过，会报错，就没法继续编译了。同时由于之前make install过，所以在/usr/local/lib下面会有Sophus的so包。这里直接把它链接到项目中来就可以使用了。
(2)包含文件写法
在代码中应该这样包含。
#include "sophus/se3.h"
#include "sophus/so3.h"
如果说在Cmake文件里没有target_linkSophus的库，那么那么有可能会出现xxxx未定义的问题。
简而言之原因是在系统包含路径中，我们刚刚利用make install拷贝了相关文件到系统路径里，但我们只包含了头文件，而头文件中是没有函数的实现的。所以会出现这个问题。函数只在头文件中声明了，却没有找到具体的函数内容，所以编译器报错了。因此需要将so包链接到项目中来。
注意，以下是错误示范。之前本以为缺少函数实现，那就把sophus源码文件夹中所有文件(包含cpp文件)都拷贝到系统路径下就可以了。
然后在代码中另外加上对cpp文件的引用。
#include "sophus/se3.h"
#include "sophus/so3.h"
#include "sophus/so3.cpp"
#include "sophus/se3.cpp"
这个方法在一开始测试的时候确实起到了作用，编译成功而且运行了。但在随后写代码的时候发现了问题，那就是在多个文件中包含cpp时，编译器会报重复定义的错误。这是之前在简单测试时没有发现的，因为简单测试的时候只是一个文件，没有多个文件多次包含。出错的原因也很简单。在cpp文件中，不像是头文件，会有防卫式声明。而所谓include的本质就是把文件中的代码插入到你指定的位置而已。所以这就相当于你在一个cpp文件A里定义了一个变量A，然后在文件B中把这个cpp A包含了进来，接着你在文件C中既包含了A又包含了B。这就相当于你在C中把A文件包含了两遍。如果是头文件自然没问题，有防卫式声明，不会重复包含。但问题是现在是cpp文件，在文件A中已经定义了一个变量A，包含文件B相当于又定义了一个变量A。同一个文件中两个变量同名，自然会报重复定义的错误了。
3.Sophus示例
下面的代码简单演示了Sophus的使用。
#include <iostream>
#include <cmath>
using namespace std;
#include <Eigen/Core>//导入eigen库的核心组件
#include <Eigen/Geometry>//导入eigen库的几何组件
#include "sophus/se3.h"
#include "sophus/so3.h"
int main(int argc, char **argv) {
// 沿Z轴转90度的旋转矩阵
Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI / 2, Eigen::Vector3d(0, 0, 1)).toRotationMatrix();
Sophus::SO3 SO3_R(R); // Sophus::SO(3)可以直接从旋转矩阵构造
Sophus::SO3 SO3_v(0, 0, M_PI / 2); // 亦可从旋转向量构造
Eigen::Quaterniond q(R); // 或者四元数
Sophus::SO3 SO3_q(q);
// 上述表达方式都是等价的
// 输出SO(3)时，以so(3)形式输出
cout << "SO(3) from matrix: " << SO3_R << endl;
cout << "SO(3) from vector: " << SO3_v << endl;
cout << "SO(3) from quaternion :" << SO3_q << endl;
// 使用对数映射获得它的李代数
Eigen::Vector3d so3 = SO3_R.log();
cout << "so3 = " << so3.transpose() << endl;
// hat 为向量到反对称矩阵
cout << "so3 hat=\n" << Sophus::SO3::hat(so3) << endl;
// 相对的，vee为反对称到向量
cout << "so3 hat vee= " << Sophus::SO3::vee(Sophus::SO3::hat(so3)).transpose() << endl; // transpose纯粹是为了输出美观一些
// 增量扰动模型的更新
Eigen::Vector3d update_so3(1e-4, 0, 0); //假设更新量为这么多
Sophus::SO3 SO3_updated = Sophus::SO3::exp(update_so3) * SO3_R;
cout << "SO3 updated = " << SO3_updated << endl;
/********************萌萌的分割线*****************************/
cout << "************我是分割线*************" << endl;
// 对SE(3)操作大同小异
Eigen::Vector3d t(1, 0, 0); // 沿X轴平移1
Sophus::SE3 SE3_Rt(R, t); // 从R,t构造SE(3)
Sophus::SE3 SE3_qt(q, t); // 从q,t构造SE(3)
cout << "SE3 from R,t= " << endl << SE3_Rt << endl;
cout << "SE3 from q,t= " << endl << SE3_qt << endl;
// 李代数se(3) 是一个六维向量，方便起见先typedef一下
typedef Eigen::Matrix<double, 6, 1> Vector6d;
Vector6d se3 = SE3_Rt.log();
cout << "se3 = " << se3.transpose() << endl;
// 观察输出，会发现在Sophus中，se(3)的平移在前，旋转在后.
// 同样的，有hat和vee两个算符
cout << "se3 hat = " << endl << Sophus::SE3::hat(se3) << endl;
cout << "se3 hat vee = " << Sophus::SE3::vee(Sophus::SE3::hat(se3)).transpose() << endl;
// 最后，演示一下更新
Vector6d update_se3; //更新量
update_se3.setZero();
update_se3(0, 0) = 1e-4d;
Sophus::SE3 SE3_updated = Sophus::SE3::exp(update_se3) * SE3_Rt;
cout << "SE3 updated = " << endl << SE3_updated.matrix() << endl;
return 0;
}
如果出现什么错误，请参考上面部分说的使用的注意事项，是不是Sophus库安装或使用方式不当。
至此，关于李代数、Sophus库的使用就介绍完了。
本文作者原创,未经许可不得转载,谢谢配合
