众所周知彩色图像是由RGB三个波段组合形成的，因此只要有分别三个波段的数据就可以进行彩色合成。不过在进行彩色合成的时候必须要面临一个问题，也就是不同波段数据可能并不是严格对准的，如下图所示。
在图中分别读取了RGB三个波段的影像数据，然后直接进行叠加，可以看到效果比较糟糕。因为三个波段并不是严格对齐的，直接叠加必然会出现重影的效果。因此，要进行彩色合成，第一步就是要对各波段进行对准。这和高光谱遥感影像的生产是相同的，各波段之间必须要进行对准才行，否则就像上面这张图一样，出现严重的重影，导致无法进行后续应用。
1.波段对齐实现思路
不同波段之间的对齐从流程上来说比较简单，这里我们假设不同波段影像之间只存在平移关系，不存在旋转和缩放变换。这种假设是合理的，对于一般传感器而言，不同波段的感光元件都是放置在同一平面上的。以RGB三波段为例，首先以R作为基准波段，将R和G波段进行匹配，找到同名点，求解单应矩阵(Homography)，找到R和G的几何关系。然后再将R和B波段进行匹配，寻找同名点，求解单应矩阵，找到R和B的对应关系。最后分别利用求出的单应矩阵，将G和B波段重采到R波段上。最后将三个波段合成，形成彩色图像。总的来说分为匹配和重采两大步骤。
这种思路是通用的，不仅仅对于普通图像，在实际的高光谱遥感影像的生产过程中也是这样实现的，只是在具体实现方式和细节上有所不同、更为复杂。对于普通图像，使用OpenCV就可以完成上述所有操作了，包括匹配、重采两大步骤。但对于遥感影像而言，OpenCV就有点力不从心了。因为遥感影像和普通影像相比太大了，动辄就是几万乘几万的分辨率，如果用OpenCV直接处理要么很慢，要么直接挂掉了。所以对于遥感影像而言，一般使用GDAL进行影像的IO以及重采等相关操作。匹配一般也不是直接使用OpenCV，而是用如SiftGPU等专门的库来实现，提升生产效率。此外还要考虑对影像进行分块匹配策略、特征提取的稳健性等其它更为复杂的问题。但这里只是为了了解流程与原理，就不谈很复杂的东西了。
2.实现代码
# coding=utf-8
import cv2
import numpy as np
import math
def drawMatches(img1, img2, good_matches):
img_out = np.hstack((img1, img2))
for match in good_matches:
pt1 = (int(match[0]), int(match[1]))
pt2 = (int(match[2] + img1.shape[1]), int(match[3]))
cv2.circle(img_out, pt1, 5, (0, 0, 255), 1, cv2.LINE_AA)
cv2.circle(img_out, pt2, 5, (0, 0, 255), 1, cv2.LINE_AA)
cv2.line(img_out, pt1, pt2, (0, 0, 255), 1, cv2.LINE_AA)
return img_out
def extractPointFromMatches(good_matches):
keypoints1 = []
keypoints2 = []
for match in good_matches:
keypoints1.append([match[0], match[1]])
keypoints2.append([match[2], match[3]])
return keypoints1, keypoints2
def calcDis(matches):
distences = []
for match in matches:
x1 = match[0]
y1 = match[1]
x2 = match[2]
y2 = match[3]
dis = math.sqrt(math.pow(x2 - x1, 2) + math.pow(y2 - y1, 2))
distences.append(dis)
return distences
def dataFilter(matches, ratio):
# 由于这里认为不同影像间仅存在平移关系
# 因此各匹配点对之间的连线距离应该是相等且斜率相等的
# 筛选也是依据这两个条件进行的
# 如果两个图像间存在别的对应关系，这个筛选条件就失效了
# 求平均值
ave_dis = 0
ave_k = 0
for match in matches:
x1 = match[0]
y1 = match[1]
x2 = match[2]
y2 = match[3]
dis = math.sqrt(math.pow(x2 - x1, 2) + math.pow(y2 - y1, 2))
k = (y2 - y1) / (x2 - x1)
ave_dis = ave_dis + dis
ave_k = ave_k + k
ave_dis = ave_dis / matches.__len__()
ave_k = ave_k / matches.__len__()
# 求标准差
stdv_dis = 0
stdv_k = 0
for match in matches:
x1 = match[0]
y1 = match[1]
x2 = match[2]
y2 = match[3]
dis = math.sqrt(math.pow(x2 - x1, 2) + math.pow(y2 - y1, 2))
k = (y2 - y1) / (x2 - x1)
stdv_dis = stdv_dis + math.pow(dis - ave_dis, 2)
stdv_k = stdv_k + math.pow(k - ave_k, 2)
stdv_dis = math.sqrt(stdv_dis / matches.__len__())
stdv_k = math.sqrt(stdv_k / matches.__len__())
# 求置信范围
range_top = ave_dis + ratio * stdv_dis
range_bottom = ave_dis - ratio * stdv_dis
range_k_top = ave_k + ratio * stdv_k
range_k_bottom = ave_k - ratio * stdv_k
print("\nave_dis " + ave_dis.__str__())
print("range_top " + range_top.__str__())
print("range_bottom " + range_bottom.__str__())
print("ave_k " + ave_k.__str__())
print("range_top_k " + range_k_top.__str__())
print("range_bottom_k " + range_k_bottom.__str__())
# 筛选
good_matches = []
for match in matches:
x1 = match[0]
y1 = match[1]
x2 = match[2]
y2 = match[3]
dis = math.sqrt(math.pow(x2 - x1, 2) + math.pow(y2 - y1, 2))
k = abs((y2 - y1) / (x2 - x1))
if dis < range_top and dis > range_bottom and k < range_k_top and k > range_k_bottom:
good_matches.append(match)
return good_matches
# FLANN+SIFT
# 由于自定义的筛选条件比较严格，开启筛选后很有可能候选点一个都不满足，但其实匹配效果还是不错的，所以默认关闭
# 而且，由于后面在计算单应矩阵时，本身也会用RANSAC筛选，所以这里可以不过滤
def FLANN_SIFT(img1, img2, flag=False):
# 新建SIFT对象，参数默认
sift = cv2.xfeatures2d_SIFT.create()
# 调用函数进行SIFT提取
kp1, des1 = cv2.xfeatures2d_SIFT.detectAndCompute(sift, img1, None)
kp2, des2 = cv2.xfeatures2d_SIFT.detectAndCompute(sift, img2, None)
if len(kp1) == 0 or len(kp2) == 0:
print("No enough keypoints.")
return
else:
print("\nkp1 size:" + len(kp1).__str__() + "," + "kp2 size:" + len(kp2).__str__())
# FLANN parameters
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
search_params = dict(checks=50) # or pass empty dictionary
flann = cv2.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(des1, des2, k=2)
good_matches = []
good_kps1 = []
good_kps2 = []
# 筛选
for i, (m, n) in enumerate(matches):
if m.distance < 0.5 * n.distance:
good_matches.append(matches[i])
good_kps1.append(kp1[matches[i][0].queryIdx])
good_kps2.append(kp2[matches[i][0].trainIdx])
if good_matches.__len__() == 0:
print("No enough good matches.")
cv2.drawKeypoints(img1, kp1, img1)
cv2.drawKeypoints(img2, kp2, img2)
cv2.imshow("img1", img1)
cv2.imshow("img2", img2)
cv2.waitKey(0)
return
else:
good_out = []
good_out_kp1 = []
good_out_kp2 = []
print("good matches:" + good_matches.__len__().__str__())
for i in range(good_kps1.__len__()):
good_out_kp1.append([good_kps1[i].pt[0], good_kps1[i].pt[1]])
good_out_kp2.append([good_kps2[i].pt[0], good_kps2[i].pt[1]])
good_out.append([good_kps1[i].pt[0], good_kps1[i].pt[1], good_kps2[i].pt[0], good_kps2[i].pt[1]])
if flag == True:
# 筛选匹配
good_out = dataFilter(good_out, 3)
good_out_kp1, good_out_kp2 = extractPointFromMatches(good_out)
img1_show = cv2.cvtColor(img1, cv2.COLOR_GRAY2BGR)
img2_show = cv2.cvtColor(img2, cv2.COLOR_GRAY2BGR)
img3 = drawMatches(img1_show, img2_show, good_out)
cv2.imshow('match result', img3)
cv2.waitKey(0)
return good_out_kp1, good_out_kp2, good_out
# 分别读取RGB三个波段数据
band_b = cv2.imread('data/01000v/b.jpg', cv2.IMREAD_GRAYSCALE)
band_g = cv2.imread('data/01000v/g.jpg', cv2.IMREAD_GRAYSCALE)
band_r = cv2.imread('data/01000v/r.jpg', cv2.IMREAD_GRAYSCALE)
# 分别对B-G、B-R进行匹配
kp1, kp2, matches1 = FLANN_SIFT(band_b, band_g)
kp3, kp4, matches2 = FLANN_SIFT(band_b, band_r)
# 依据匹配的特征点求解不同波段间的变换关系
# 同时这里要注意对不同匹配结果的应对措施
# 如果一对同名点都没有匹配到，那就直接原图搬过去
# 如果匹配到小于4对同名点，无法计算单应矩阵，那就通过求解偏移的平均值手动构造
# 如果正常匹配到很多对点，利用OpenCV求解单应矩阵
if kp1 is None:
homo1 = np.array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
elif kp1.__len__() < 4:
x1 = 0
y1 = 0
x2 = 0
y2 = 0
for i in range(kp1.__len__()):
x1 = x1 + kp1[i][0]
y1 = y1 + kp1[i][1]
x2 = x2 + kp2[i][0]
y2 = y2 + kp2[i][1]
x1 = x1 / kp1.__len__()
x2 = x2 / kp1.__len__()
y1 = y1 / kp1.__len__()
y2 = y2 / kp1.__len__()
dx = x2 - x1
dy = y2 - y1
homo1 = np.array([[1, 0, dx],
[0, 1, dy],
[0, 0, 1]])
else:
homo1, mask1 = cv2.findHomography(np.array(kp2), np.array(kp1), cv2.RANSAC)
if kp3 is None:
homo2 = np.array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
elif kp3.__len__() < 4:
x1 = 0
y1 = 0
x2 = 0
y2 = 0
for i in range(kp3.__len__()):
x1 = x1 + kp3[i][0]
y1 = y1 + kp3[i][1]
x2 = x2 + kp4[i][0]
y2 = y2 + kp4[i][1]
x1 = x1 / kp1.__len__()
x2 = x2 / kp1.__len__()
y1 = y1 / kp1.__len__()
y2 = y2 / kp1.__len__()
dx = x2 - x1
dy = y2 - y1
homo2 = np.array([[1, 0, dx],
[0, 1, dy],
[0, 0, 1]])
else:
homo2, mask2 = cv2.findHomography(np.array(kp4), np.array(kp3), cv2.RANSAC)
print("Homography between B and G band")
print(homo1)
print("Homography between B and R band")
print(homo2)
# 依据求得的单应矩阵对波段进行重采
resampled_band_g = cv2.warpPerspective(band_g, homo1, (band_g.shape[1], band_g.shape[0]))
resampled_band_r = cv2.warpPerspective(band_r, homo2, (band_r.shape[1], band_r.shape[0]))
# 将不同波段合并成新的彩色图像
img = np.zeros([band_b.shape[0], band_b.shape[1], 3], np.uint8)
img[:, :, 0] = band_b
img[:, :, 1] = resampled_band_g
img[:, :, 2] = resampled_band_r
# 直接读取的RGB波段叠加形成的彩色影像
img2 = np.zeros([band_b.shape[0], band_b.shape[1], 3], np.uint8)
img2[:, :, 0] = band_b
img2[:, :, 1] = band_g
img2[:, :, 2] = band_r
cv2.imshow("Resample band data", img)
cv2.imshow("Overlay band data", img2)
cv2.waitKey(0)
3.测试实验
分别利用上述代码进行了多次实验如下。实验数据来自于Prokudin-Gorskii Collection，地址是这里。这组照片主要拍摄于1905-1915年之间，是分别用红绿蓝不同的滤光镜拍摄同一目标，得到的不同波段的底片。正如上面说的，由于不同波段的相片并不是同一瞬间拍摄完成的，所以不同波段间的底片并不是严格对齐的，直接叠加就会出现博客开头的效果。所以需要先对不同波段进行重采，从而实现“完美”融合。
上面分别是BGR各波段之间的匹配结果以及直接叠加和波段对准后的对比。可以很明显的看出波段对准后效果就非常棒了。下面是其它照片合成后的效果。
通过我们的代码，让一百多年前的古老的照片重新焕发了生机，不再只是黑白灰的世界，而是丰富的彩色世界。在我第一次运行出结果时是很震撼的，仿佛一下子把我带回了一个多世纪以前，莫名有种与历史对话的感觉。因为之前看过去的照片都是黑白的，脑海里自然形成了过去的世界都是黑白的这种概念，突然现在看到了彩色的过去的照片，有点不习惯了。有一种一百年前的人原来也和我们生活在同一个世界，他们的世界也是彩色的这种感觉。
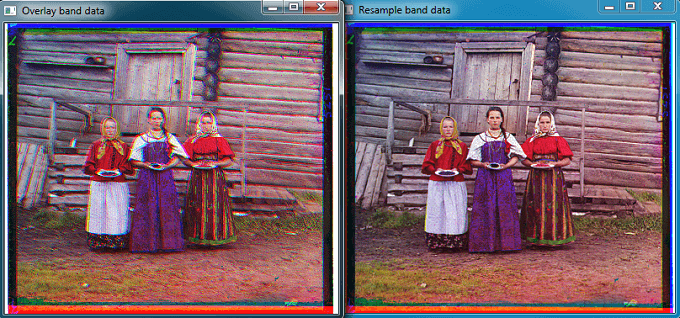
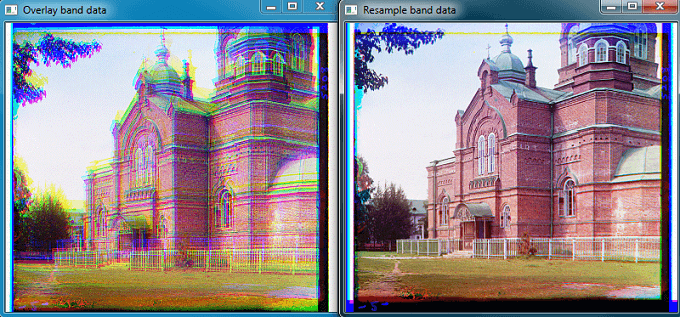
4.另一种方法
在OpenCV中还提供了另一种相对简便的方法实现谱段配准。在OpenCV中有函数findTransformECC()可以用于实现这个需求，中文名叫使用增强的相关系数图像配准（ECC）最大化。下面直接贴代码。
import cv2
import numpy as np
def get_gradient(im):
# Calculate the x and y gradients using Sobel operator
grad_x = cv2.Sobel(im, cv2.CV_32F, 1, 0, ksize=3)
grad_y = cv2.Sobel(im, cv2.CV_32F, 0, 1, ksize=3)
# Combine the two gradients
grad = cv2.addWeighted(np.absolute(grad_x), 0.5, np.absolute(grad_y), 0.5, 0)
return grad
if __name__ == '__main__':
# Read 8-bit color image.
# This is an image in which the three channels are
# concatenated vertically.
band_b = cv2.imread('data/01000v/b.jpg', cv2.IMREAD_GRAYSCALE)
band_g = cv2.imread('data/01000v/g.jpg', cv2.IMREAD_GRAYSCALE)
band_r = cv2.imread('data/01000v/r.jpg', cv2.IMREAD_GRAYSCALE)
# Find the width and height of the color image
sz = band_r.shape
print sz
height = sz[0]
width = sz[1]
# Extract the three channels from the gray scale image
# and merge the three channels into one color image
im_color = np.zeros((height, width, 3), dtype=np.uint8)
# for i in xrange(0, 3):
# im_color[:, :, i] = im[i * height:(i + 1) * height, :]
im_color[:, :, 0] = band_b
im_color[:, :, 1] = band_g
im_color[:, :, 2] = band_r
# Allocate space for aligned image
im_aligned = np.zeros((height, width, 3), dtype=np.uint8)
# The blue and green channels will be aligned to the red channel.
# So copy the red channel
im_aligned[:, :, 2] = im_color[:, :, 2]
# Define motion model
warp_mode = cv2.MOTION_HOMOGRAPHY
# Set the warp matrix to identity.
if warp_mode == cv2.MOTION_HOMOGRAPHY:
warp_matrix = np.eye(3, 3, dtype=np.float32)
else:
warp_matrix = np.eye(2, 3, dtype=np.float32)
# Set the stopping criteria for the algorithm.
criteria = (cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 5000, 1e-10)
# Warp the blue and green channels to the red channel
for i in xrange(0, 2):
(cc, warp_matrix) = cv2.findTransformECC(get_gradient(im_color[:, :, 2]), get_gradient(im_color[:, :, i]),
warp_matrix, warp_mode, criteria)
if warp_mode == cv2.MOTION_HOMOGRAPHY:
# Use Perspective warp when the transformation is a Homography
im_aligned[:, :, i] = cv2.warpPerspective(im_color[:, :, i], warp_matrix, (width, height),
flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP)
else:
# Use Affine warp when the transformation is not a Homography
im_aligned[:, :, i] = cv2.warpAffine(im_color[:, :, i], warp_matrix, (width, height),
flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP)
print warp_matrix
# Show final output
cv2.imshow("Color Image", im_color)
cv2.imshow("Aligned Image", im_aligned)
cv2.waitKey(0)
这段代码来源于这个网页，并对图像读取部分稍作了修改。运行后效果如下图所示，可以看到效果也是很不错的。
而采用这种方法和上面的那种方法比较，同样的一幅图片，ECC算法相对要慢很多，但结果却和上面的方法相差无几。一幅300多分辨率的图像三通道配准需要一分多钟，这个速度确实很慢了。这样根本没办法处理更大的遥感图像。暂时还不清楚为什么会这样。这样下面是同样一幅图片(394×340)波段对齐后的效果，上面是自己写的方法，下面是ECC方法。
使用自己实现的方法，用时0.36s。
使用OpenCV自带ECC方法，用时110s。
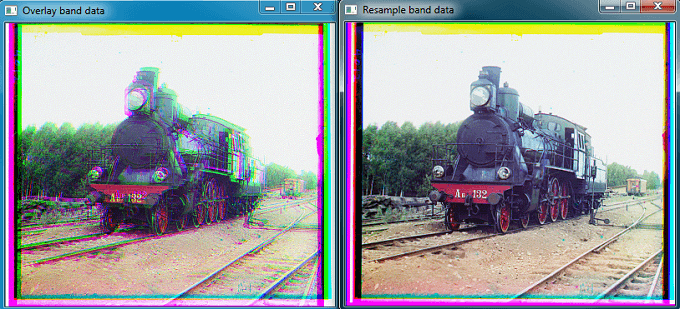
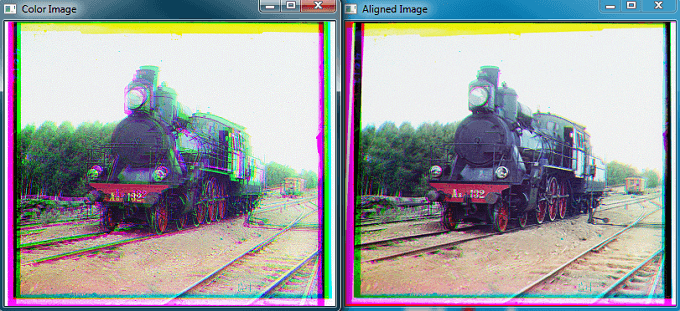
可以看到对齐效果没有差别，但耗时却是305倍。
虽然说ECC方法是OpenCV内置的方法，但也不一定就是万能的，如下对于下面这张图(512×504)，ECC方法不仅慢，而且失效了，但自己写的方法效果很好。
直接叠加
自己写的方法，耗时0.9秒。
OpenCV的ECC方法，耗时190秒。
实验用到的这几张图片可能不太好下(国外地址，下载可能网速较慢)，已经传到百度云里了，可以直接下载测试。 链接：https://pan.baidu.com/s/10xmh0iFtlY_2HUU1VVsosw 密码：hweq。
5.参考资料
- https://www.learnopencv.com/image-alignment-ecc-in-opencv-c-python
- https://www.loc.gov/pictures/collection/prok/
本文作者原创,未经许可不得转载,谢谢配合
