灰度拉伸及其在遥感影像预处理中的应用

1.灰度拉伸原理
2.灰度拉伸实现
3.遥感影像预处理应用
4.总结
5.参考资料

在之前OpencV的这篇笔记中说到了直方图均衡化，其实就是灰度拉伸的一种特殊形式。灰度拉伸英文为GrayScale Stretch。而所谓灰度拉伸，简单理解就是如果一张图像的原始灰度范围是A到B，而现在通过某种算法(对应关系)，使得图像灰度一一映射到了C到D，这就可以称作灰度拉伸。而根据算法的不同大体可以分为线性和非线性两大类。在线性拉伸中，又可以分为全局线性拉伸和分段线性拉伸。顾名思义全局线性拉伸就是只使用一种对应关系，而分段线性拉伸则是每段都有各自的对应关系。非线性拉伸中包含了如对数拉伸、高斯拉伸、平方根拉伸等等算法。本文的主要内容是简单介绍各种灰度拉伸算法以及在Python下实现2%线性灰度拉伸算法，然后以一个遥感影像处理中的实例来说明具体应用效果。在实现部分也会涉及一些Numpy矩阵运算优化的内容。

1.灰度拉伸原理

(1)线性灰度拉伸

线性灰度拉伸是最简单也是最常用的一种拉伸方法，设f(x,y)和g(x,y)分别表示拉伸前的图像和拉伸后的图像。拉伸前的图像f(x,y)中最小灰度用A表示，最大灰度用B表示。拉伸后的图像g(x,y)中最小灰度用C表示，最大灰度用D表示。f(i,j)和g(i,j)分别表示图像中(i,j)处的灰度值。有以下公式。

\[g(i,j)=\frac{D-C}{B-A}(f(i,j)-A)+C\]

这个公式通用、完整说明了线性灰度拉伸的算法，对于8bit灰度图而言，如将图像拉伸到0-255，也就是C=0，D=255，公式变为如下形式。

\[g(i,j)=\frac{255}{B-A}(f(i,j)-A)\]

(2)分段线性灰度拉伸

其实原理与线性灰度拉伸是相同的，在各段中依然使用上面的公式，不同的是对于原图中不同的灰度段采用不同的线性对应关系。公式中相乘的系数，系数越大表示对该段灰度拉伸越大，从感官上就是对比度增强了。分段线性拉伸一般可用于需要对图像高频低频分别处理的时候，如抑制低频部分(灰度值较小的部分)，提升高频部分(灰度值较大的部分)对比度或单纯增加图像暗部对比度，亮部对比度不变等等。分段数量没有限制，根据实际需求处理即可。下面以分三段为例，公式如下。首先进行一些符号说明，在原图f(x,y)中，设灰度范围为A到B，第一段灰度范围为A-f1，第二段为f1-f2，第三段为f2-B。同理在变换后的图像g(x,y)中，设灰度范围为C到D，第一段灰度范围为C-g1，第二段为g1-g2，第三段为g2-D。因此由线性公式很容易得出各分段的公式，如下。

\[g(i,j) \begin{cases} \frac{g_{1}-C}{f_{1}-A}(f(i,j)-A)+C & \text{ if } f(i,j)<f_{1} \\ \frac{g_{2}-g_{1}}{f_{2}-f_{1}}(f(i,j)-f_{1})+g_{1} & \text{ if } f_{1}\leq f(i,j)\leq f_{2} \\ \frac{D-g_{2}}{B-f_{2}}(f(i,j)-f_{2})+g_{2} & \text{ if } f(i,j)>f_{2} \end{cases}\]

公式看起来很复杂，但其实很简单，只需要把各段的最大最小值带入线性公式就可以得到了。如果依然以8bit图像(0-255)举例，公式会简单一些。

\[g(i,j) \begin{cases} \frac{g_{1}}{f_{1}}f(i,j) & \text{ if } f(i,j)<f_{1} \\ \frac{g_{2}-g_{1}}{f_{2}-f_{1}}(f(i,j)-f_{1})+g_{1} & \text{ if } f_{1}\leq f(i,j)\leq f_{2} \\ \frac{255-g_{2}}{255-f_{2}}(f(i,j)-f_{2})+g_{2} & \text{ if } f(i,j)>f_{2} \end{cases}\]

这里f1、f2、g1、g2在0-255之间随意取值，当然f2要大于f1，g2要大于g1。例如f1=70，f2=150，g1=50，g2=200。这样的变换意义是将拉伸原图中中频区域，抑制低频和高频区域，也就是说使灰度值在70-150之间的对比度增强，使暗部和亮部对比度都降低。

(3)2%灰度线性拉伸

这种算法是ENVI在使用的灰度拉伸算法之一，相比于直接灰度线性拉伸，效果要好一些。何为2%，其实指的是首尾的2%个像素。基于直方图分布，对图像灰度值分布在2%和98%之间的像素做线性拉伸，即拉伸时去除小于2%大于98%的值，这样绝大多数的异常值会在拉伸时舍掉，显示出漂亮直观的效果。简而言之就是，去掉首尾各占像素总数2%的像素，将剩下的像素重新拉伸到满灰度范围(如0-255)。要实现这个拉伸需要两步，一步是灰度统计，统计2%和98%对应的灰度值，第二步是将2%和98%对应的灰度值重新拉伸到满灰度范围。

(4)对数变换

所谓对数变换，是指原灰度与新灰度是对数关系，公式如下，也比较简单。对数变换可以将图像的低灰度值部分扩展，显示出低灰度部分更多的细节，将其高灰度值部分压缩，减少高灰度值部分的细节，从而达到强调图像低灰度部分的目的。对于不同的底数，底数越大，对低灰度部分的扩展就越强，对高灰度部分的压缩也就越强。可以通过画出函数曲线图直观感受一下。

\[s = c\cdot log_{v+1}(1+v\cdot r),r\in [0,1]\]

在不乘以常数c的情况下，整个公式的输出范围为0到1。其中r是归一化后的灰度值(取值在0到1之间)，c是常数，即灰度范围的最大值，在8bit图像中即取256。v则是调节参数，可以取10、100、200等数值，通过调节不同的v值，结果也会有所不同。v越大，其对暗部对比度的提升就越明显。

(5)伽马变换

公式如下。

\[s=cr^{\gamma },r\in[0,1]\]

不乘以常数从，整个公式输入灰度范围为0到1，输出也为0到1。其中，r依旧为归一化灰度值，c依旧为常数(灰度范围最大值，8bit则是256)。伽马变换对图像的修正作用其实就是通过增强低灰度或高灰度的细节实现的。γ值以1为分界，值越小，对图像低灰度部分的扩展作用就越强，值越大，对图像高灰度部分的扩展作用就越强，通过不同的γ值，就可以达到增强低灰度或高灰度部分细节的作用。伽马变换对于图像对比度偏低，并且整体亮度值偏高(相机过曝)情况下的图像增强效果明显。

(6)直方图均衡化

前面也说了，直方图均衡化也是灰度变换的一种，如果感兴趣可以看那篇博客，有比较详细的介绍。这里再提另一个与均衡化类似的概念——直方图规定化，又叫直方图匹配。直方图均衡化算法可以自动确定灰度变换函数，从而获得具有均匀直方图的输出图像。它主要用于增强动态范围偏小的图像对比度，丰富图像的灰度级。这种方法的优点是操作简单，且结果可以预知，当图像需要自动增强时是一种不错的选择。

但有时我们希望可以对变换过程加以控制，如能够人为地修正直方图的形状，或者说获得具有指定直方图的输出图像，这样就可以有选择地增强某个灰度范围内的对比度或使图像灰度值满足某种特定的分布。这种用于产生具有特定直方图图像的方法叫做直方图规定化，或直方图匹配。

直方图规定化是在运用均衡化原理的基础上，通过建立原始图像和期望图像(待匹配直方图的图像)之间的关系，使原始图像的直方图匹配特定的形状，从而弥补直方图均衡不具备交互作用的特性。更多详细内容可参考参考资料[1]。

2.灰度拉伸实现

由于各算法基本除了公式之外其它基本大同小异，因此这里只实现ENVI中比较常用的而且稍微复杂点的2%线性拉伸算法。

# coding=utf-8
import cv2
import numpy as np


def hist_calc(img, ratio):
    bins = np.arange(256)
    # 调用Numpy实现灰度统计
    hist, bins = np.histogram(img, bins)
    total_pixels = img.shape[0] * img.shape[1]
    # 计算获得ratio%所对应的位置，
    # 这里ratio为0.02即为2%线性化，0.05即为5%线性化
    min_index = int(ratio * total_pixels)
    max_index = int((1 - ratio) * total_pixels)
    min_gray = 0
    max_gray = 0
    # 统计最小灰度值(A)
    sum = 0
    for i in range(hist.__len__()):
        sum = sum + hist[i]
        if sum > min_index:
            min_gray = i
            break
    # 统计最大灰度值(B)
    sum = 0
    for i in range(hist.__len__()):
        sum = sum + hist[i]
        if sum > max_index:
            max_gray = i
            break
    return min_gray, max_gray


def linearStretch(img, new_min, new_max, ratio):
    # 获取原图除去2%像素后的最小、最大灰度值(A、B)
    old_min, old_max = hist_calc(img, ratio)
    # 对原图中所有小于或大于A、B的像素都赋为A、B
    img1 = np.where(img < old_min, old_min, img)
    img2 = np.where(img1 > old_max, old_max, img1)
    print('old min = %d,old max = %d' % (old_min, old_max))
    print('new min = %d,new max = %d' % (new_min, new_max))
    # 按照线性拉伸公式计算新的灰度值
    img3 = np.uint8((new_max - new_min) / (old_max - old_min) * (img2 - old_min) + new_min)
    return img3


img = cv2.imread("test.png", cv2.IMREAD_GRAYSCALE)
# 第二、三个参数分别为新的最大最小灰度值(C、D)
# 0.02即为2%线性灰度拉伸
res = linearStretch(img, 1, 255, 0.02)
cv2.imshow("image", img)
cv2.imshow("result", res)
cv2.waitKey(0)

运行结果如下。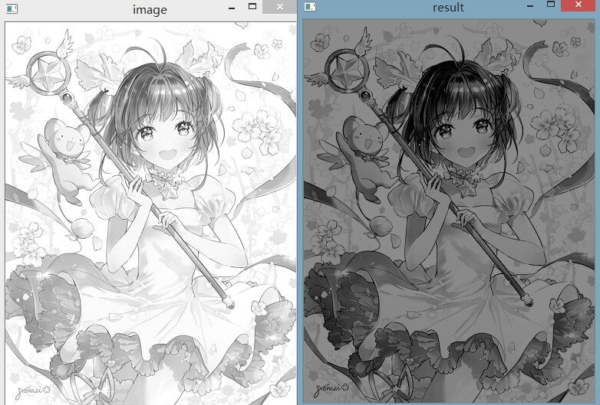可以看到，和原图相比结果图像暗了很多，这是因为原图整体偏亮导致的。

此外在代码中有一些需要注意的地方。首先是效率问题。由于图像是一个Numpy矩阵，因此要尽可能使用矩阵的整体运算，而不要自己再写两个for循环遍历各个元素，这样会严重拖慢速度。其次是一些Numpy常用函数的使用，如类型转换等。这在遥感影像处理中很常用，如经常需要把16bit量化的数据转成8bit。最后是要善用np.where()函数，十分有用。这种差别可能在小图像上体现的不是很明显，但在遥感影像这种大图上，体现的就非常明显了。在下面会有直观的感受。

简单说一下对数拉伸这种非线性运算的拉伸。在实际写代码的过程中如果直接按照上述公式来实现会发现耗时特别长，图像越大越明显。如下代码分别演示了处理1500*1500大小图像的情况。

# coding=utf-8
import numpy as np
import cv2
import math
import time


def logTransform(img, v=200, c=256):
    img_normalized = img * 1.0 / c
    log_res = c * (np.log(1 + v * img_normalized) / np.log(v + 1))
    img_new = np.uint8(log_res)
    return img_new


def logTransformOrigin(img, v=200, c=256):
    new_img = img
    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            pixel_normalized = img[i, j] / 256.0
            log_pixel = np.uint8(c * math.log(1 + v * pixel_normalized, 1 + v))
            new_img[i, j] = log_pixel
    return new_img


img = cv2.imread("E:\\join\\join.png", cv2.IMREAD_GRAYSCALE)
t1 = time.time()
logTransformOrigin(img)
t2 = time.time()
logTransform(img)
t3 = time.time()

print t2 - t1
print t3 - t2

直接使用公式遍历计算耗时7.28秒，而采用换底公式改写公式后耗时0.0069秒。这里使用了numpy的log函数而不是math的，因为numpy的log函数可以对矩阵进行整体计算，效率会比遍历高很多。

3.遥感影像预处理应用

在遥感影像中提取特征点匹配一直是一个比较基础和重要的问题，然而受限于遥感影像本身质量等很多因素的影响，如果直接对影像进行处理很有可能收获不到想要的效果。因此必须要在进行进一步处理之前对影像进行灰度拉伸、去噪等预处理。这里只讨论灰度拉伸问题，不讨论去噪问题，这在之前的这篇博客中已经讨论过了。

首先先放一个结果，下图是直接利用GDAL读取的同一片CCD不同波段的影像原始数据，没有经过任何处理直接使用FLANN+SURF进行匹配。在左图中提取到了835个特征点，右图中只提取到了7个特征点，一共找到了10对匹配点。仔细放大会发现匹配的几乎都是错的。可以看到效果非常不理想，和想象的差距非常远。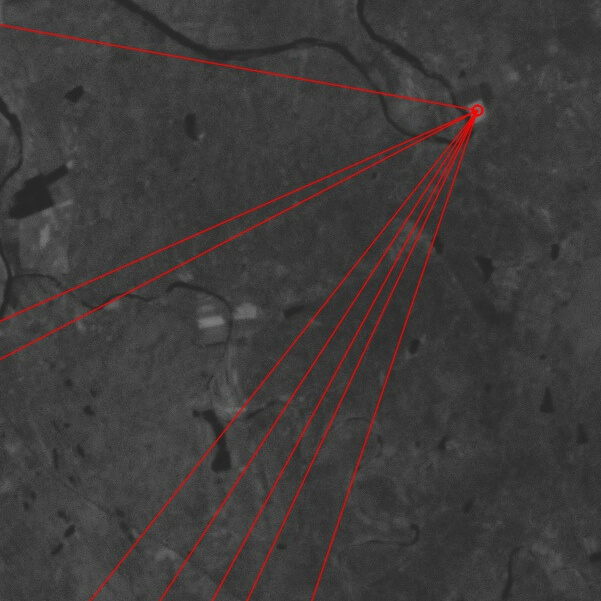而使用2%线性灰度拉伸后，效果如下，在左图中提取到了9120个特征点，右图中提取到了7481个特征点，一共匹配到了1631对点，效果很好。而且经过灰度拉伸的处理，两幅影像的明暗程度也比较接近了。所以可见预处理对后续处理流程的重要性。下面是Python利用GDAL对遥感影像进行预处理的代码。

# coding=utf-8
from osgeo import gdal
from gdalconst import *
import cv2
import numpy as np
import time


def hist_calc(img, ratio):
    bins = np.arange(256)
    hist, bins = np.histogram(img, bins)
    total_pixels = img.shape[0] * img.shape[1]
    min_index = int(ratio * total_pixels)
    max_index = int((1 - ratio) * total_pixels)
    min_gray = 0
    max_gray = 0
    sum = 0
    for i in range(hist.__len__()):
        sum = sum + hist[i]
        if sum > min_index:
            min_gray = i
            break
    sum = 0
    for i in range(hist.__len__()):
        sum = sum + hist[i]
        if sum > max_index:
            max_gray = i
            break
    return min_gray, max_gray


def linearStretch(img, new_min, new_max, ratio):
    old_min, old_max = hist_calc(img, ratio)
    img1 = np.where(img < old_min, old_min, img)
    img2 = np.where(img1 > old_max, old_max, img1)
    print('old min = %d,old max = %d' % (old_min, old_max))
    print('new min = %d,new max = %d' % (new_min, new_max))
    img3 = np.uint8((new_max - new_min) / (old_max - old_min) * (img2 - old_min) + new_min)
    return img3


def loadIMGintoMem(img_path):
    # 以只读方式打开遥感影像
    dataset = gdal.Open(img_path, GA_ReadOnly)

    # 获取影像的第一个波段
    band_1 = dataset.GetRasterBand(1)

    # 读取第一个波段中读取指定范围数据
    data = band_1.ReadAsArray(0, 0, band_1.XSize, band_1.YSize)
    return data


def loadImageWithSlideWindow(img_path, start_x, start_y, x_range, y_range):
    # 以只读方式打开遥感影像
    dataset = gdal.Open(img_path, GA_ReadOnly)

    # 获取影像的第一个波段
    band_1 = dataset.GetRasterBand(1)

    # 读取第一个波段中读取指定范围数据
    data = band_1.ReadAsArray(start_x, start_y, x_range, y_range)
    return data


img = loadImageWithSlideWindow("N:\\D1923-561-32_rc.tif", 0, 8000, 500, 500)
# 转换影像为8bit数据
img_8 = np.uint8(img / 4)
res = linearStretch(img_8, 1, 255, 0.02)
cv2.imshow("original", img_8)
cv2.imshow("stretch", res)
cv2.waitKey(0)

下面是运行代码的对比图，分别是灰度拉伸处理前后的影像。可以看到差别非常明显。在原始数据中，灰度范围为42-81，而拉伸后则为1-255，效果明显变好了。这也就是之前用ENVI保存的影像进行实验处理效果都很好，但自己用GDAL读取数据处理效果就不太好的原因。因为ENVI在输出图像时自动进行了相关的灰度拉伸，所以处理的效果很好。但是自己读取的话，读取的就是原始数据，自然处理效果不好了。

在解决了“有没有”的问题之后就是“好不好”的问题。代码的运行效率是考量的因素之一。下面的代码分别是自己写的for循环版本的2%灰度拉伸和直接用矩阵运算版本的对比。

# coding=utf-8
from osgeo import gdal
from gdalconst import *
import cv2
import numpy as np
import time


def hist_calc(img, ratio):
    bins = np.arange(256)
    hist, bins = np.histogram(img, bins)
    total_pixels = img.shape[0] * img.shape[1]
    min_index = int(ratio * total_pixels)
    max_index = int((1 - ratio) * total_pixels)
    min_gray = 0
    max_gray = 0
    sum = 0
    for i in range(hist.__len__()):
        sum = sum + hist[i]
        if sum > min_index:
            min_gray = i
            break
    sum = 0
    for i in range(hist.__len__()):
        sum = sum + hist[i]
        if sum > max_index:
            max_gray = i
            break
    return min_gray, max_gray


def linearStretch(img, new_min, new_max, ratio):
    old_min, old_max = hist_calc(img, ratio)
    img1 = np.where(img < old_min, old_min, img)
    img2 = np.where(img1 > old_max, old_max, img1)
    print('old min = %d,old max = %d' % (old_min, old_max))
    print('new min = %d,new max = %d' % (new_min, new_max))
    img3 = np.uint8((new_max - new_min) / (old_max - old_min) * (img2 - old_min) + new_min)
    return img3


def loadIMGintoMem(img_path):
    # 以只读方式打开遥感影像
    dataset = gdal.Open(img_path, GA_ReadOnly)

    # 获取影像的第一个波段
    band_1 = dataset.GetRasterBand(1)

    # 读取第一个波段中读取指定范围数据
    data = band_1.ReadAsArray(0, 0, band_1.XSize, band_1.YSize)
    return data


def loadImageWithSlideWindow(img_path, start_x, start_y, x_range, y_range):
    # 以只读方式打开遥感影像
    dataset = gdal.Open(img_path, GA_ReadOnly)

    # 获取影像的第一个波段
    band_1 = dataset.GetRasterBand(1)

    # 读取第一个波段中读取指定范围数据
    data = band_1.ReadAsArray(start_x, start_y, x_range, y_range)
    return data


def gray_sta(img, ratio):
    # 对图像进行灰度统计
    total_pixels = img.shape[0] * img.shape[1]
    flatten_img = img.flatten()
    sort_img = np.sort(flatten_img)
    min_index = int(ratio * total_pixels)
    max_index = int((1 - ratio) * total_pixels)
    gray_min = sort_img[min_index]
    gray_max = sort_img[max_index]
    return gray_min, gray_max


def img_process(img, new_min, new_max, ratio):
    # 采用2%灰度直方图分段线性拉伸
    old_min, old_max = gray_sta(img, ratio)
    img_out = np.zeros([img.shape[0], img.shape[1]], np.uint8)
    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            if img[i, j] <= old_min:
                img_out[i, j] = 1
            elif img[i, j] > old_max:
                img_out[i, j] = 255
            else:
                img_out[i, j] = ((new_max - new_min) / (old_max - old_min)) * (
                        img[i, j] - old_min) + new_min
    return img_out


img = loadImageWithSlideWindow("N:\\D1923-561-32_rc.tif", 0, 8000, 1500, 2500)
# 转换为8bit图像
img_8 = np.uint8(img / 4)
t1 = time.time()
res1 = linearStretch(img_8, 1, 255, 0.02)
t2 = time.time()
res2 = img_process(img_8, 1, 255, 0.02)
t3 = time.time()
print('dt1:' + (t2 - t1).__str__())
print('dt2:' + (t3 - t2).__str__())
cv2.imwrite("res1.jpg", res1)
cv2.imwrite("res2.jpg", res2)

原图以及运算结果和耗时分别如下图。原图矩阵运算结果 for循环结果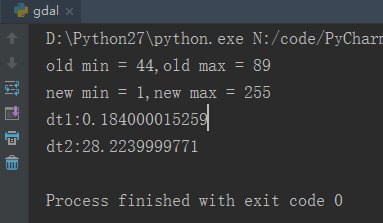耗时对比可以看到从运行结果上来看，整体差别不是很大，虽然采用手动for循环的结果白色地物更亮一些，但耗时也是十分可观的。基于矩阵运算的结果尽管没有那么好，但是和原图比已经好很多了，有点差别但几乎可以忽略不计。但它的耗时却非常短。矩阵运算耗时0.18秒，for循环耗时28.22秒，差了156倍。所以这点结果的牺牲是可以接受的，更何况导致结果差异并不是运算方式不同造成的，而是由于本身算法设计造成的，修改一下结果就应该会一样了。这里只是为了演示，就并不去仔细研究为什么结果不同，要修改哪里了。