在上一篇博客中介绍了计算机视觉领域的开山角点描述子——Moravec算子。但同时也看到,它还存在着很多问题,例如只能在指定方向上对灰度进行计算、对边缘有较强响应等。 本篇博客主要学习实现Moravec算子的升级版——Harris算子。相比于Moravec算子,Harris算子在实际中有非常广泛的应用。
小小的吐槽一下,如果想对某些算法原理追根溯源,还是建议去国外网站上查相关资料吧。为了找Harris的论文,百度了好久,各种CSDN博客几乎翻了个遍,一个引用原始论文的都没看见。只是感叹CSDN博客质量确实良莠不齐。在WiKi上一搜Corner Detection词条,查下Harris算子的相关引用,很方便的就找到论文了。
1.Harris算子介绍
Harris角点算子的简历如下:
- 提出者:Harris and Stephens
- 提出时间:1988
- 相关论文:A combined corner and edge detector(相比于Moravec的那篇,这篇文档质量好太多了)
- 一句话总结: Moravec算子的改进版,更加稳定
2.Harris算子原理
在之前介绍Moravec算子的时候说过,它的缺点主要有三个方面:
- 一是Moravec算子各向异性响应(Anisotropic Response),简单来说就是它只在4个方向对梯度进行了计算,无法获取任意方向梯度
- 二是Moravec算子在计算CRF时由于采用等权求和,导致其对噪声较为敏感,易受噪声干扰(Noise Response)
- 三是Moravec算子对边缘有较强响应(Large Response of Edge),容易出现误检。
针对这三点,Harris依次提出了三个方法来改进Moravec算子。
(1)灰度梯度近似
相比于Moravec算子固定方向上的梯度感知,Harris算子在数学上对灰度变化进行了更为精确的逼近,与Moravec算子中灰度变化不同的是通过合理的选择(u,v)可以对任何方向的灰度变化进行测度。论文原文截图如下:

(2)高斯权重
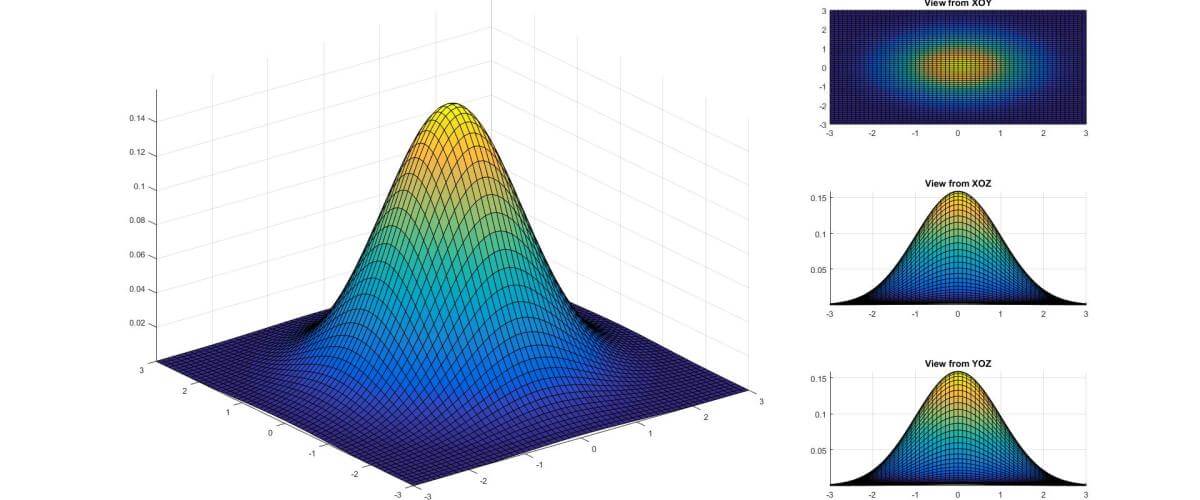
相较于Moravec的方形窗口,Harris通过采用二维高斯分布的权重,使得形成了一个圆形窗口。离中心越近的像素权重越大,而离中心越远,权重越小。
一个二维高斯分布的示意图如下所示。
论文中相关表述如下。
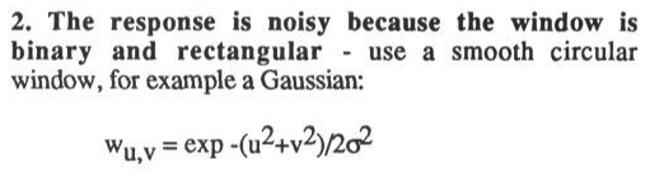
(3)改进的角点测度函数
为了减轻Moravec算子中对边缘的强响应,Harris提出了一个全新的角点测度方法。通过将灰度变化写成矩阵形式进而从矩阵运算角度提出了方案。由于M是对称阵,所以主对角线元素即为特征值,通过比较两个特征值之间的关系对角点进行判断。论文相关部分如下:

在实际计算中,采用如下方法会更快一些。

3.Harris算子实现
Harris算子的实现相对简单。相对复杂的是指定大小的二维高斯模板生成。难点在于小数的取整,对于一些常用的高斯模板会有一定的出入,并不严格的是向上、向下或四舍五入取整。而且与参数也有关,收集了几个常用参数如下:
# win_size=5, sigma=1.4
# win_size=5, sigma=1
# win_size=7, sigma=0.84089642
# win_size=3, sigma=0.8
获取指定大小及σ的高斯模板函数如下。
def getGaussianFilter(win_size=3, sigma=0.8):
xs = []
ys = []
g_xys = []
g_xys_normal = []
g_xys_int = []
cen_x = win_size / 2
cen_y = win_size / 2
for i in range(win_size):
for j in range(win_size):
cen_i = i - cen_x
cen_j = j - cen_y
g_xy = (1 / (2.0 * math.pi * sigma * sigma)) * \
math.pow(math.e, -(cen_i * cen_i + cen_j * cen_j) / (2.0 * sigma * sigma))
xs.append(i)
ys.append(j)
g_xys.append(g_xy)
scale_num = 1.0 / sum(g_xys)
for i in range(g_xys.__len__()):
g_xys_normal.append(g_xys[i] * scale_num)
filter = np.zeros([win_size, win_size])
for i in range(win_size):
for j in range(win_size):
filter[i, j] = g_xys_normal[i * win_size + j]
min_num = min(g_xys_normal)
for i in range(g_xys_normal.__len__()):
g_xys_int.append(int(g_xys_normal[i] / min_num))
filter_int = np.zeros([win_size, win_size])
for i in range(win_size):
for j in range(win_size):
filter_int[i, j] = g_xys_int[i * win_size + j]
return filter, filter_int
依据论文中的公式依次计算A、B、C以及R。k一般取0.04-0.06之间。K越大计算出的R越小,相同阈值下提取的角点越少。
def calcIx(win):
win = np.int32(win)
size = win.shape[1] - 2
Ix = np.zeros([size, size], np.int32)
for j in range(win.shape[0]):
for i in range(1, win.shape[1] - 1):
Ix[j, i - 1] = win[j, i + 1] - win[j, i - 1]
return Ix
def calcIy(win):
win = np.int32(win)
size = win.shape[0] - 2
Iy = np.zeros([size, size], np.int32)
for j in range(1, win.shape[0] - 1):
for i in range(win.shape[1]):
Iy[j - 1, i] = win[j + 1, i] - win[j - 1, i]
return Iy
def calcCornerResponse(img, i, j, gauss_kernel, win_size=3, k=0.04):
winX = getXWindow(img, i, j, win_size)
Ix = calcIx(winX)
winY = getYWindow(img, i, j, win_size)
Iy = calcIy(winY)
Ix2 = Ix * Ix
Iy2 = Iy * Iy
IxIy = Ix * Iy
A = np.sum((gauss_kernel * Ix2) / np.sum(gauss_kernel))
B = np.sum((gauss_kernel * Iy2) / np.sum(gauss_kernel))
C = np.sum((gauss_kernel * IxIy) / np.sum(gauss_kernel))
det_M = A * B - C * C
trace_M = A + B
R = det_M - k * trace_M * trace_M
return R
完整代码及测试数据见Github项目,点击查看。
4.测试

 相较于Moravec,Harris的效果好很多,但依然也会存在一些问题,需要后续其它的改进。
相较于Moravec,Harris的效果好很多,但依然也会存在一些问题,需要后续其它的改进。
5.参考资料
- [1]https://en.wikipedia.org/wiki/Corner_detection
- [2]https://en.wikipedia.org/wiki/Harris_Corner_Detector
- [3]http://www.bmva.org/bmvc/1988/avc-88-023.pdf
- [4]https://blog.csdn.net/kezunhai/article/details/11265167
- [5]http://www.360doc.com/content/15/1114/16/25664332_513168246.shtml
- [6]https://blog.csdn.net/luoshixian099/article/details/48244255
本文作者原创,未经许可不得转载,谢谢配合
