- 1.Introduction
- 2.Vanishing Points
- 3.Perspective Projection
- 4.Rotations and Translations
- 5.Dolly Zoom
- 6.Feeling of Camera Motion
- 7.How to Compute Intrinsics from Vanishing Points
- 8.Camera Calibration
- 9.Assignment Dolly Zoom
Robotics:Perception课程Week1的测验与作业习题,如果有错误的地方欢迎提出、交流。注意本博客中的题目与答案仅供学习交流使用,严禁用于抄袭等不守信行为。若因抄袭答案导致Coursera账号被取消激活,本博客概不负责。
1.Introduction
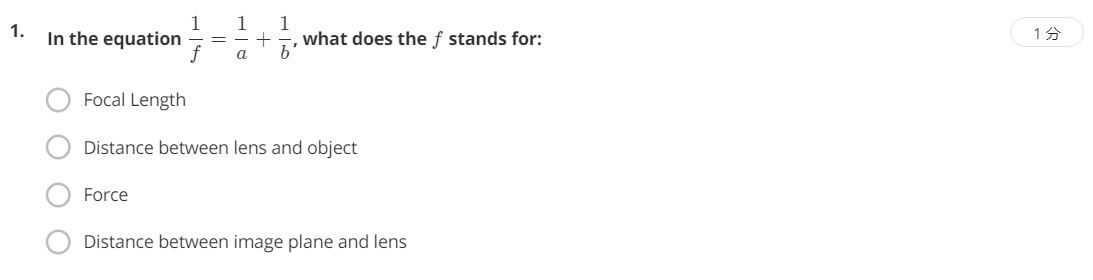 考察的是透镜成像模型的成像公式中各变量的含义,f表示焦距,a表示物距,b表示像距,所以选择A,”Focal Length”。
考察的是透镜成像模型的成像公式中各变量的含义,f表示焦距,a表示物距,b表示像距,所以选择A,”Focal Length”。
 考察对焦过程中的变化情况。由于改变了像距b,所以成像公式也不再成立,同时影像开始变得模糊。选择A和B。
考察对焦过程中的变化情况。由于改变了像距b,所以成像公式也不再成立,同时影像开始变得模糊。选择A和B。
 考察近大远小的成像规律:
考察近大远小的成像规律:
由上式可知,a增大时,y会变小,本题应该是False。
 False。只有当平行线所在平面与像面平行时,在影像中才会保持平行,否则投影后都不再平行。
False。只有当平行线所在平面与像面平行时,在影像中才会保持平行,否则投影后都不再平行。
 和上题一样。只有当线平行于像面时才会保持平行,应选择A。
和上题一样。只有当线平行于像面时才会保持平行,应选择A。
 False。考察灭点的概念。正如题中所说,灭点是现实世界中一组平行线在像面上的投影线的交点。而在像面中可以有多对现实世界中平行的线,因此也就会有多个交点,这些交点都是灭点。多个灭点连接形成灭影线。
False。考察灭点的概念。正如题中所说,灭点是现实世界中一组平行线在像面上的投影线的交点。而在像面中可以有多对现实世界中平行的线,因此也就会有多个交点,这些交点都是灭点。多个灭点连接形成灭影线。
 答案不全。选B。这个绘图仪的性质。
答案不全。选B。这个绘图仪的性质。
2.Vanishing Points
 考察灭点的定义。很简单,在图像中选取一组现实世界中的平行线,然后找交点即可,可以发现交点是C。
考察灭点的定义。很简单,在图像中选取一组现实世界中的平行线,然后找交点即可,可以发现交点是C。
 和上一题同理,可以找多组平行线,然后这些灭点所在的直线即为地平线。答案为l3。
和上一题同理,可以找多组平行线,然后这些灭点所在的直线即为地平线。答案为l3。
 和上一题一样,连接平行线找交点,结果是l1。
和上一题一样,连接平行线找交点,结果是l1。
 很显然是False的。灭点并不一定在影像中,没有必然联系。
很显然是False的。灭点并不一定在影像中,没有必然联系。
 True。由灭点组成的灭影线表示无穷远处。
True。由灭点组成的灭影线表示无穷远处。
3.Perspective Projection
 由题可知,a=2,b=2,c=-2√2。再根据公式:
由题可知,a=2,b=2,c=-2√2。再根据公式:
可以算出θ为45度,ρ为1,选D。
 还是根据上面的公式,这里θ为45度,ρ为3,将上面式子中的a、b、c依次带入即可算出结果,选A。
还是根据上面的公式,这里θ为45度,ρ为3,将上面式子中的a、b、c依次带入即可算出结果,选A。
 考察齐次坐标系下空间直线的表示方法。在齐次坐标系中,直线用其上两个点的向量叉乘得到。所以对(1,2,1)和(-1,3,1)做叉乘,结果为(-1,-2,5)。选项中对应关系正确的是A。
考察齐次坐标系下空间直线的表示方法。在齐次坐标系中,直线用其上两个点的向量叉乘得到。所以对(1,2,1)和(-1,3,1)做叉乘,结果为(-1,-2,5)。选项中对应关系正确的是A。
 齐次坐标系中,求两条直线的交点,用表示两条直线的向量叉乘即可,叉乘结果为(1,-1,2),对应关系正确的是D。
齐次坐标系中,求两条直线的交点,用表示两条直线的向量叉乘即可,叉乘结果为(1,-1,2),对应关系正确的是D。
 考察直线的齐次坐标表示以及直线角点求法。y=1直线用齐次坐标表示,不妨任意取其上的两个点:(0,1,1)、(2,1,1)。这两个点都在z=1的像面上,且满足y=1条件。将这两个向量做叉乘,即可得到y=1的齐次表示为(0,2,-2)。同理y=2可求出为(0,2,-4)。求两条直线的交点做叉乘,得到(-4,0,0),等价于k(1,0,0)。所以应该选B、C。
考察直线的齐次坐标表示以及直线角点求法。y=1直线用齐次坐标表示,不妨任意取其上的两个点:(0,1,1)、(2,1,1)。这两个点都在z=1的像面上,且满足y=1条件。将这两个向量做叉乘,即可得到y=1的齐次表示为(0,2,-2)。同理y=2可求出为(0,2,-4)。求两条直线的交点做叉乘,得到(-4,0,0),等价于k(1,0,0)。所以应该选B、C。
4.Rotations and Translations
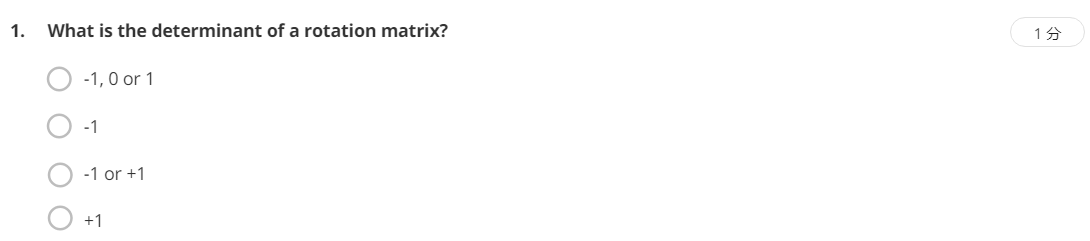 考察旋转矩阵的性质。由于旋转矩阵是正交阵,等价于问正交阵的行列式是多少。由正交阵性质:转置等于逆,所以有AA^T=E。对等式两边取行列式,有|AA^T|=|E|,单位阵的行列式值为1,所以|AA^T|=1。又由矩阵行列式的性质:矩阵转置的行列式等于其本身的行列式,所以|A|=|A^T|,所以|A|^2=1,所以|A|的解为正负1。但由于旋转矩阵的特殊性,行列式为-1的情况被舍去,最终答案应该是1,选D。
考察旋转矩阵的性质。由于旋转矩阵是正交阵,等价于问正交阵的行列式是多少。由正交阵性质:转置等于逆,所以有AA^T=E。对等式两边取行列式,有|AA^T|=|E|,单位阵的行列式值为1,所以|AA^T|=1。又由矩阵行列式的性质:矩阵转置的行列式等于其本身的行列式,所以|A|=|A^T|,所以|A|^2=1,所以|A|的解为正负1。但由于旋转矩阵的特殊性,行列式为-1的情况被舍去,最终答案应该是1,选D。
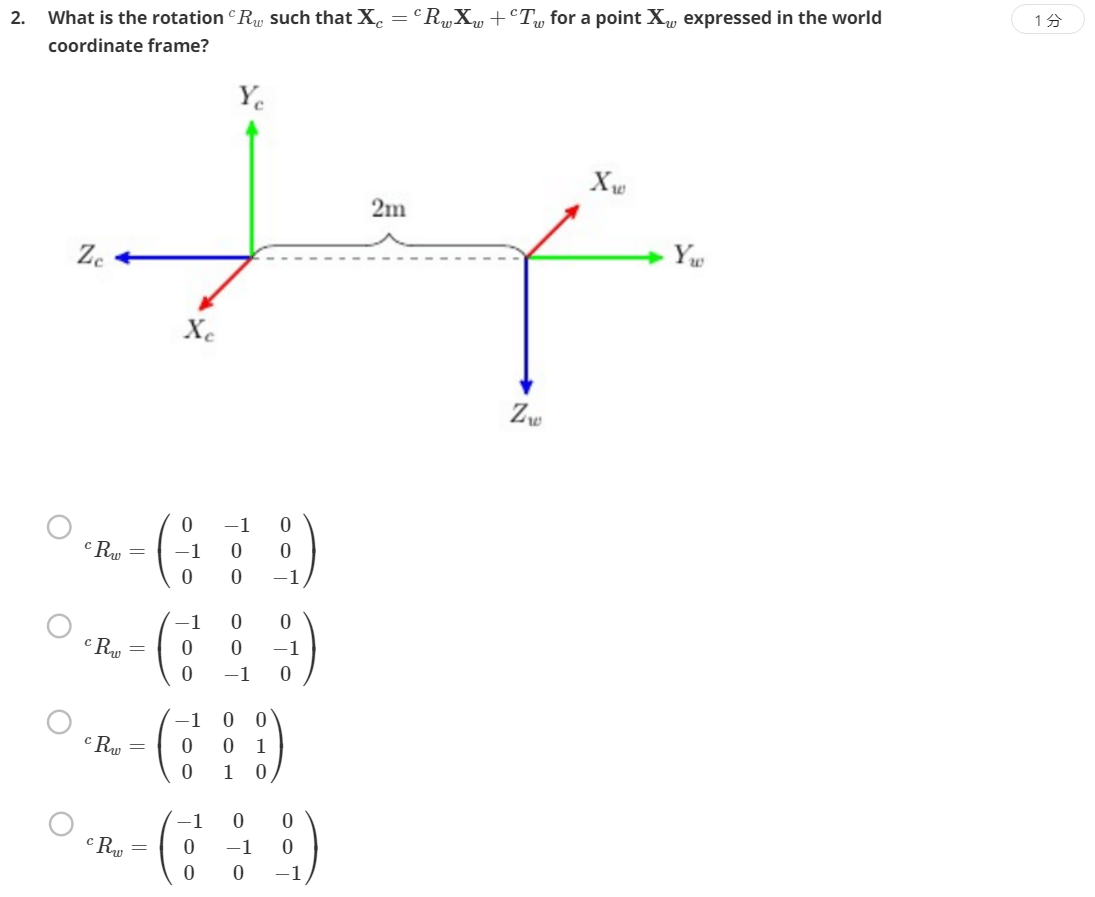 考察旋转矩阵的定义。题目中问的是\({}^{c}\textrm{R}_{w}\),也就是在Camera坐标系下World坐标系的旋转矩阵。World坐标系的x轴在Camera坐标系下表示是(-1,0,0),y轴表示为(0,0,-1),z轴表示为(0,-1,0)。所以组合成旋转矩阵应该选B。
考察旋转矩阵的定义。题目中问的是\({}^{c}\textrm{R}_{w}\),也就是在Camera坐标系下World坐标系的旋转矩阵。World坐标系的x轴在Camera坐标系下表示是(-1,0,0),y轴表示为(0,0,-1),z轴表示为(0,-1,0)。所以组合成旋转矩阵应该选B。
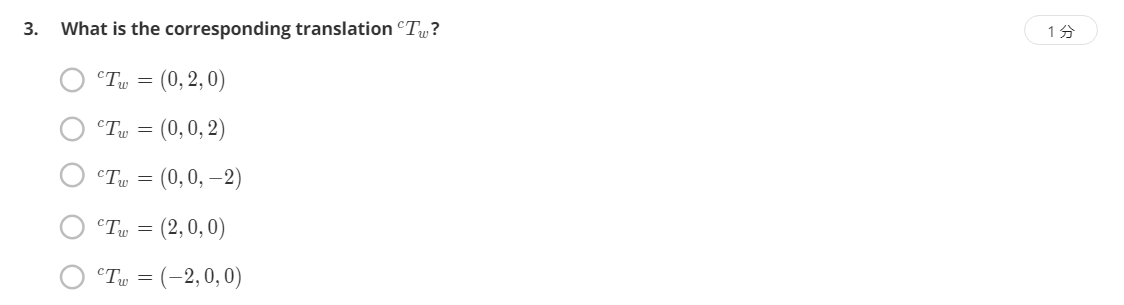 同理,同样是考察平移的定义。题目中问的是\({}^{c}\textrm{T}_{w}\),也就是从Camera到World的平移,由图可知,World坐标系的原点在Camera坐标系中为(0,0,-2),应选C。
同理,同样是考察平移的定义。题目中问的是\({}^{c}\textrm{T}_{w}\),也就是从Camera到World的平移,由图可知,World坐标系的原点在Camera坐标系中为(0,0,-2),应选C。
 注意题目中问的是\({}^{w}\textrm{R}_{c}\),也就是Camera坐标系相对于World坐标系的旋转,类似的,Camera坐标系的x轴在World坐标系中表示为(-1,0,0),y轴为(0,0,-1),z轴为(0,-1,0),组合成旋转矩阵,应选B。
注意题目中问的是\({}^{w}\textrm{R}_{c}\),也就是Camera坐标系相对于World坐标系的旋转,类似的,Camera坐标系的x轴在World坐标系中表示为(-1,0,0),y轴为(0,0,-1),z轴为(0,-1,0),组合成旋转矩阵,应选B。
 同理,题目中问的是Camera坐标系相对于World坐标系的平移,由图可知应为(0,-2,0),选C。
同理,题目中问的是Camera坐标系相对于World坐标系的平移,由图可知应为(0,-2,0),选C。
 看清题目问的是什么,题目问的是Body坐标系相对于Camera坐标系的旋转,两种思路,一是分别找到Body坐标系的x、y、z在Camera坐标系下的表示,然后拼成旋转矩阵;二是直接用旋转合成的方式计算旋转矩阵。
看清题目问的是什么,题目问的是Body坐标系相对于Camera坐标系的旋转,两种思路,一是分别找到Body坐标系的x、y、z在Camera坐标系下的表示,然后拼成旋转矩阵;二是直接用旋转合成的方式计算旋转矩阵。
第一种方式:根据右手定则,Body坐标系的z轴竖直向上,Camera坐标系竖直向下,所以z轴在Camera坐标系下的表示为(0,0,-1)。对于Body的x、y轴,可以按照下图进行分解,向量的模长为1:
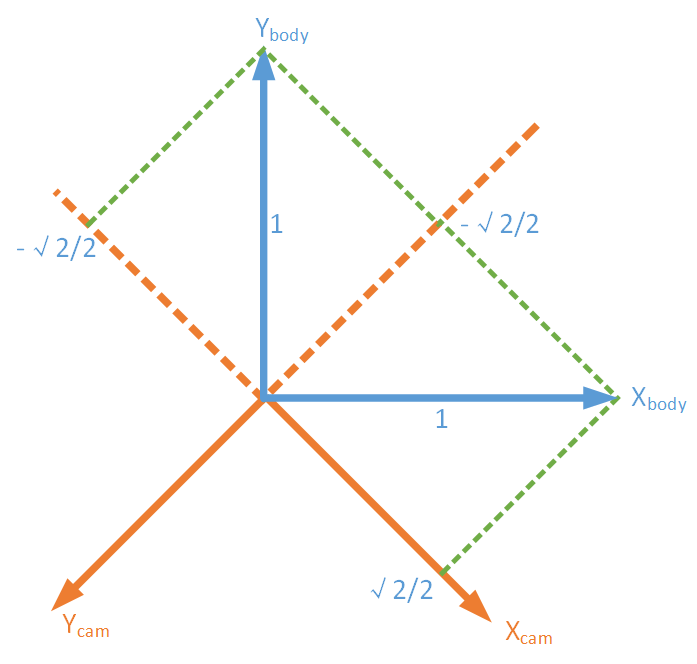 因此Body坐标系的x轴在Camera坐标系下表示为(√2/2,√2/2,0),y轴为(-√2/2,√2/2,0)。因此最终形成的旋转矩阵为:
因此Body坐标系的x轴在Camera坐标系下表示为(√2/2,√2/2,0),y轴为(-√2/2,√2/2,0)。因此最终形成的旋转矩阵为:
第二种方式:按照旋转合成。有多种旋转方式。例如Body坐标系先绕z轴转45度Rz,45,然后再绕x轴转180度得到Rx180,将两个旋转矩阵相乘即可。注意之前提到的构造“黄金法则”:下一次的旋转总是以上一次为起点,并且遵循右乘。还要注意旋转角度的正负问题,一般定义逆时针为正,顺时针为负。如果有时想象不出来到底是顺时针还是逆时针,可以用这个简单的判断方法:用手握住旋转轴并且大拇指指向旋转轴正向,按照旋转方向进行旋转,先碰到的轴的字母比后碰到的大,当前旋转方向为负,先碰到的比后碰到的小,当前旋转方向为正。这在之前的这篇博客中也有提到。
例如由Body到Camera,可以先绕Body坐标系z轴旋转45度(顺时针),所以旋转角为负。然后再将Body坐标系绕x轴旋转180度。根据旋转合成法则可以得到如下式子:
\[R_{z,-45}R_{x,180}=\begin{pmatrix} cos(-45) & -sin(-45) & 0\\ sin(-45) & cos(-45) & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 & 0\\ 0 & cos(180) & -sin(180)\\ 0 & sin(180) & cos(180) \end{pmatrix}\]最终进行矩阵运算化简可以得到:
\[\begin{pmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} & 0\\ -\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} & 0\\ 0 & 0 & -1 \end{pmatrix}\]除了这种旋转顺序还有其它的顺序,如先绕x轴旋转180度,再绕z轴旋转45度,得到的结果是一样的。还是可以按照上面的准则判断。首选,绕x轴旋转180度,此时Body坐标系的z轴向下,在此基础上绕z轴旋转45度。注意这里旋转的45度符号应为正。因为顺着z轴看去是顺时针转了45度,也就是说对着z轴看逆时针转45度。如果不好理解可以用刚刚的方法。用手握住z轴并指向z轴正向(垂直纸面向里),然后按顺时针方向旋转,先碰到的是x轴,然后是y轴,先碰到的字母比后碰到的小,所以当前旋转方向为正向。可以得到如下式子:
\[R_{x,180}R_{z,45}=\begin{pmatrix} 1 & 0 & 0\\ 0 & cos(180) & -sin(180)\\ 0 & sin(180) & cos(180) \end{pmatrix}\begin{pmatrix} cos(45) & -sin(45) & 0\\ sin(45) & cos(45) & 0\\ 0 & 0 & 1 \end{pmatrix}\]经过计算得到的结果和上面一样。因此本题选A。
 题目问的是Camera坐标系下Body的平移,由图可知,Body坐标系沿Camera坐标系x轴负向移动了4cm,沿z轴负向移动了3cm(注意Camera坐标系的z轴正向是向下的)。所以答案为(-0.04,0.-0.03),应选B。
题目问的是Camera坐标系下Body的平移,由图可知,Body坐标系沿Camera坐标系x轴负向移动了4cm,沿z轴负向移动了3cm(注意Camera坐标系的z轴正向是向下的)。所以答案为(-0.04,0.-0.03),应选B。
5.Dolly Zoom
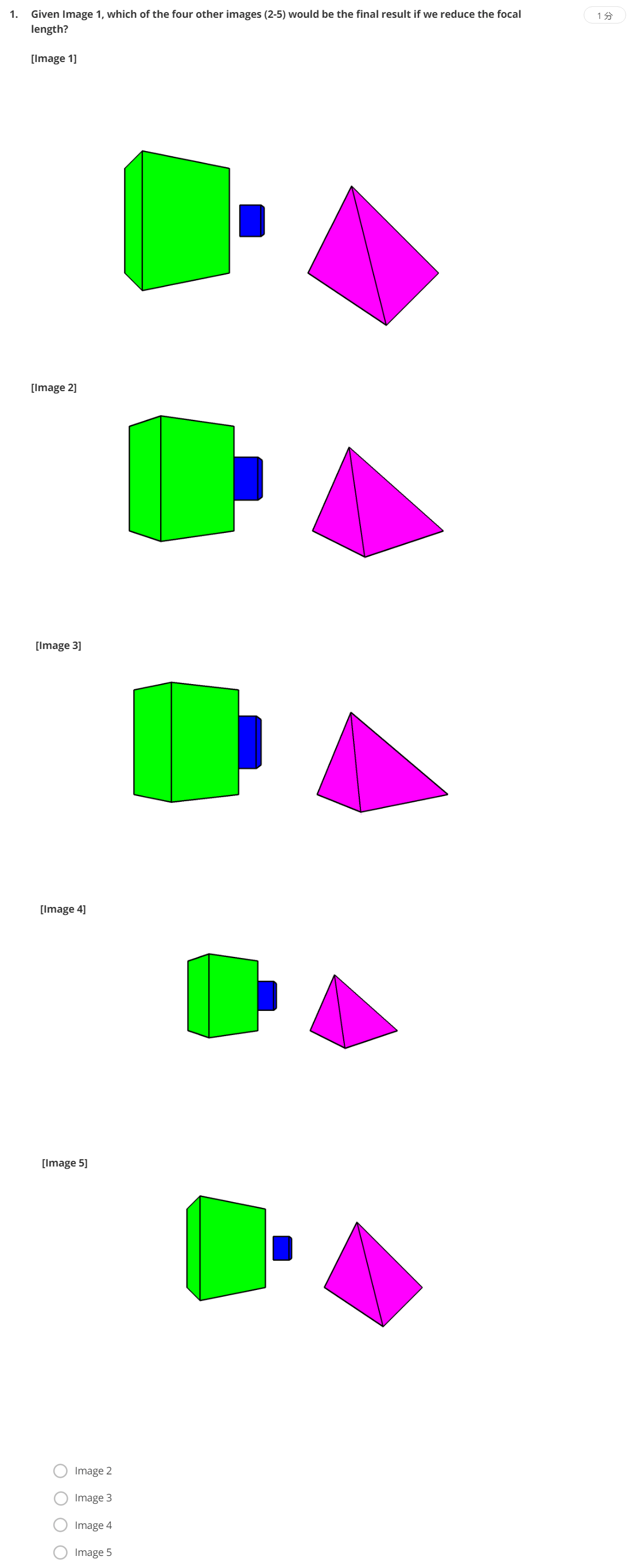 考察对Dolly Zoom效果的理解,保持前景物体不变,背景物体随着焦距的增加以及相机的远离,背景物体逐渐变大。但题目中说的是以第一张图片为参考,减小焦距的结果。随着相机逐渐远离,物体会慢慢变小,而减小焦距,根据成像大小公式,也会导致物体变小。所以应该选Image5,E。
考察对Dolly Zoom效果的理解,保持前景物体不变,背景物体随着焦距的增加以及相机的远离,背景物体逐渐变大。但题目中说的是以第一张图片为参考,减小焦距的结果。随着相机逐渐远离,物体会慢慢变小,而减小焦距,根据成像大小公式,也会导致物体变小。所以应该选Image5,E。
 和上一题类似,应该选Image3,C。
和上一题类似,应该选Image3,C。
6.Feeling of Camera Motion
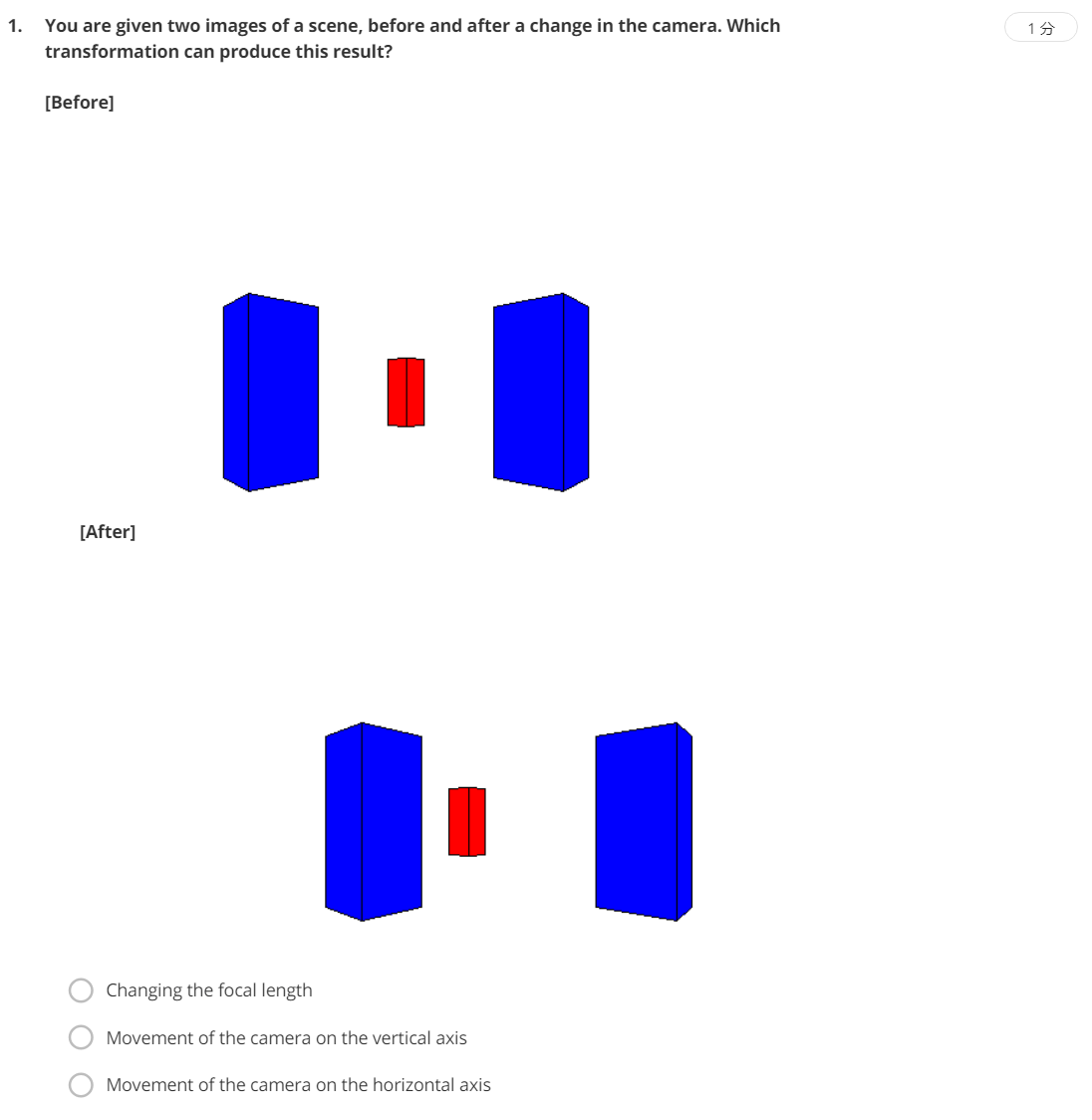 这题很明显是相机在水平方向上有运动,所以选C。
这题很明显是相机在水平方向上有运动,所以选C。
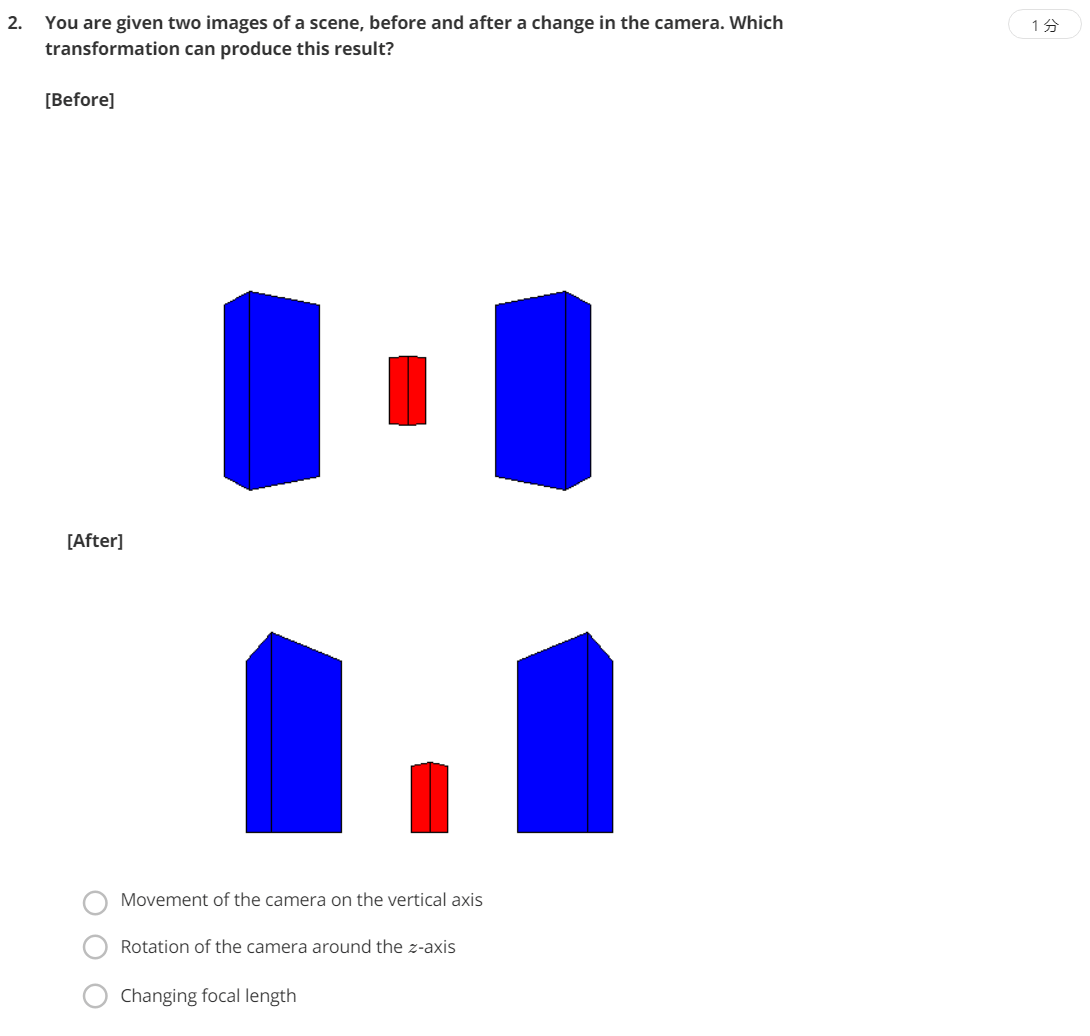 这题很明显是相机在竖直方向上有运动,所以选A。
这题很明显是相机在竖直方向上有运动,所以选A。
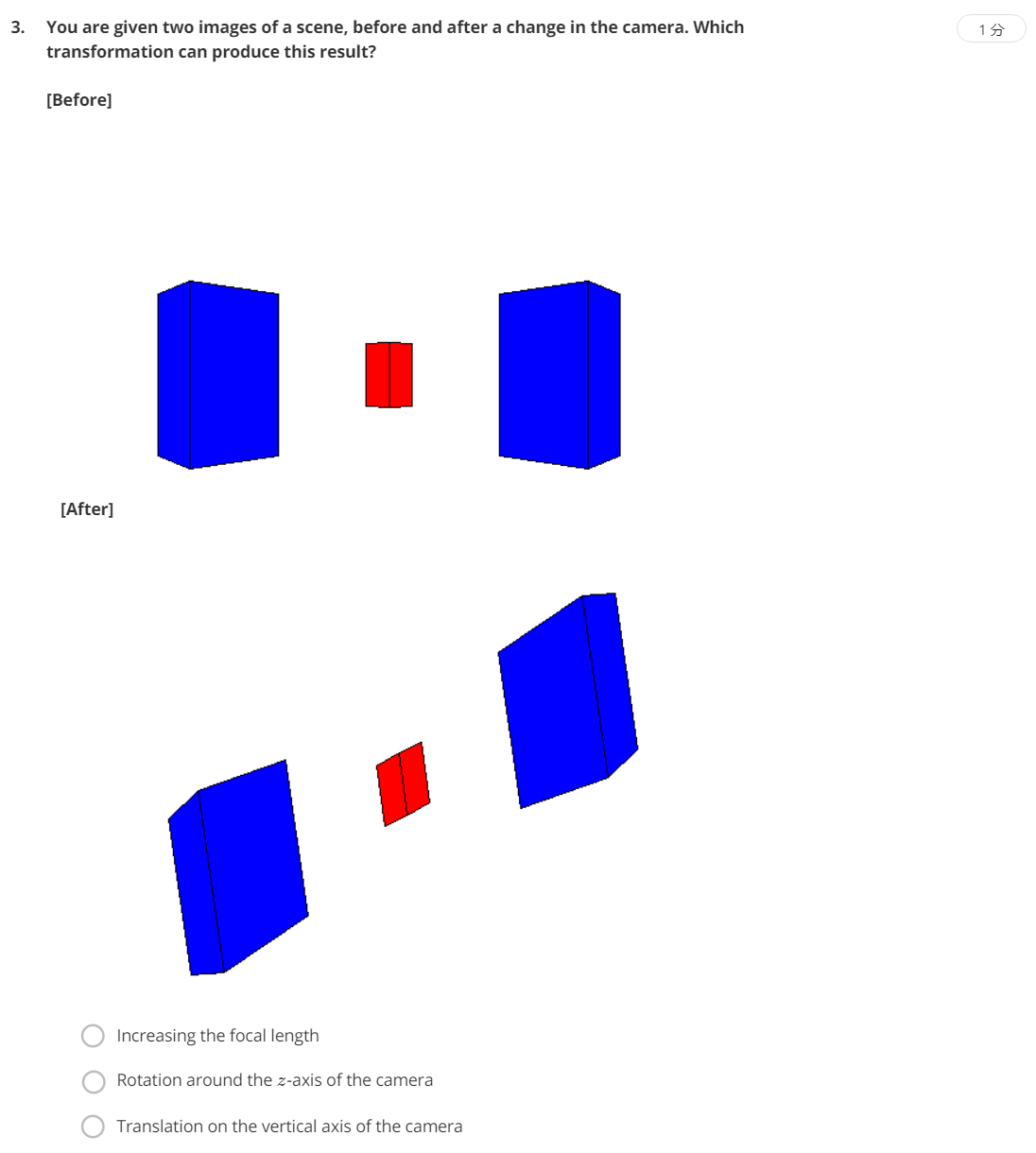 图片中的物体向左旋转,相机绕z轴向右旋转。如果不好理解可以用手机试试。
图片中的物体向左旋转,相机绕z轴向右旋转。如果不好理解可以用手机试试。
7.How to Compute Intrinsics from Vanishing Points
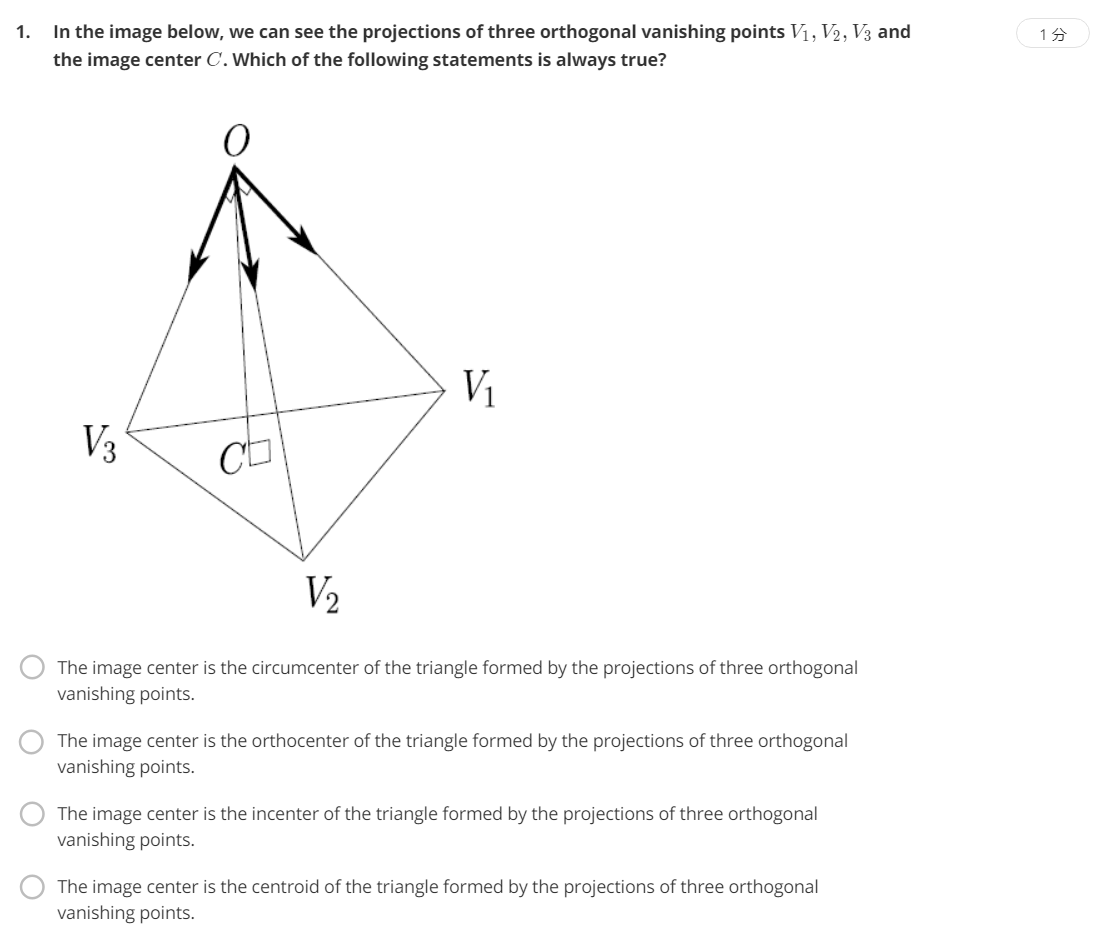 C点是OC的垂足,OC是高,C点叫做三角形的垂心,选B。circumcenter是外接圆中心,orthocenter是垂心,incenter是内接圆圆心,centroid是质心。
C点是OC的垂足,OC是高,C点叫做三角形的垂心,选B。circumcenter是外接圆中心,orthocenter是垂心,incenter是内接圆圆心,centroid是质心。
 还是对原理的考察,至少要有交点才可以计算。
还是对原理的考察,至少要有交点才可以计算。
8.Camera Calibration
 标定可以获得相机的内参(焦距、主点)以及畸变参数,所以选D。
标定可以获得相机的内参(焦距、主点)以及畸变参数,所以选D。
 题目问的是哪两张图片受径向畸变影响最大,很明显是A和D。
题目问的是哪两张图片受径向畸变影响最大,很明显是A和D。
 在标定的过程中,需要知道标定板的尺寸(格子数),所以是True。
在标定的过程中,需要知道标定板的尺寸(格子数),所以是True。
9.Assignment Dolly Zoom
题目要求是在Matlab中实现Dolly Zoom的效果,点击查看题目的代码和说明,提取码:h7b4。需要补充的是计算焦距以及相机位置的代码。根据pdf说明文件中的公式2,计算f的过程如下:

第二个是要保证前景物体大小不变的情况下调整背景物体的大小,具体公式推导如下:

最后动态演示效果如下:
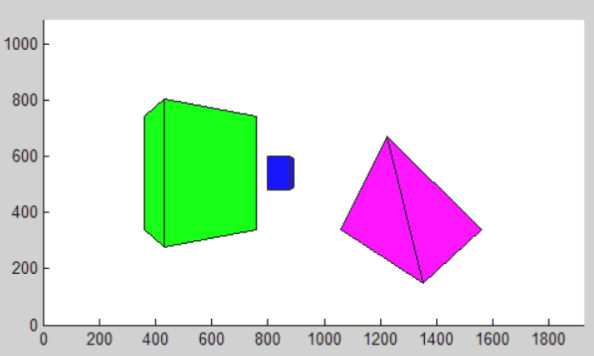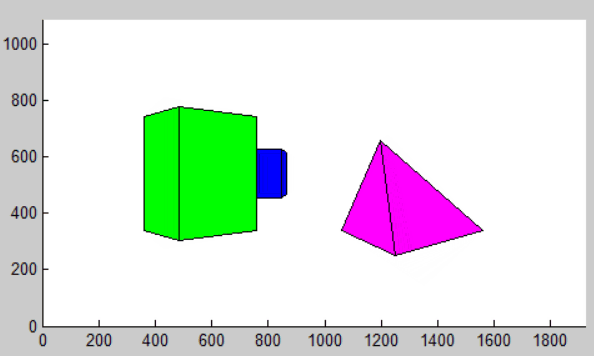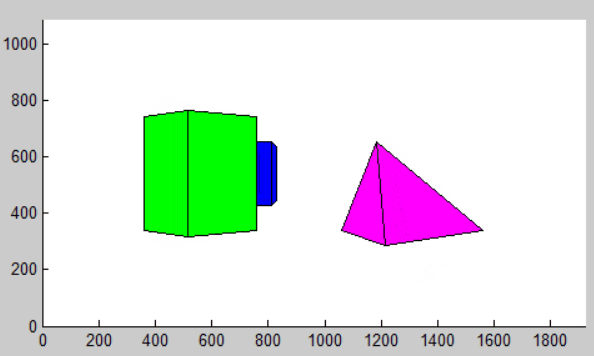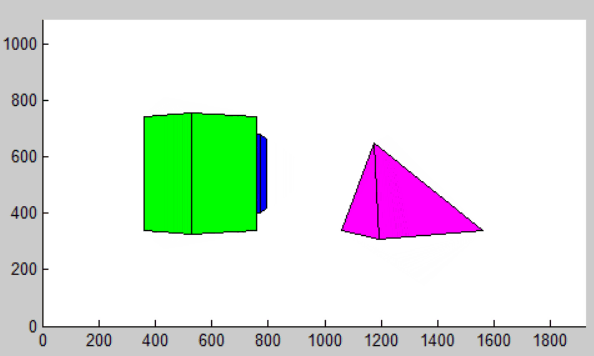
改变背景物体高度为前景的一半结果如下:
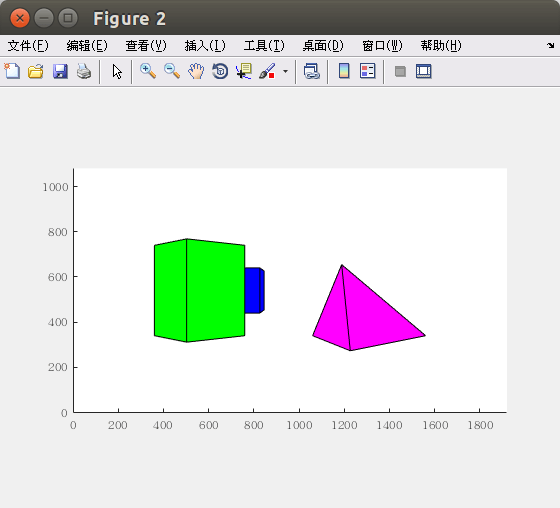
完成的代码点击这里下载,提取码:zs0e。
本文作者原创,未经许可不得转载,谢谢配合
