- 1.Homogeneous Coordinates
- 2.Projective Transformation
- 3.Vanishing Points
- 4.Cross Ratios and Single View Metrology
- 5.Assignment-Image Projection using Homographies
Robotics:Perception课程Week2的测验与作业习题,如果有错误的地方欢迎提出、交流。注意本博客中的题目与答案仅供学习交流使用,严禁用于抄袭等不守信行为。若因抄袭答案导致Coursera账号被取消激活,本博客概不负责。
1.Homogeneous Coordinates
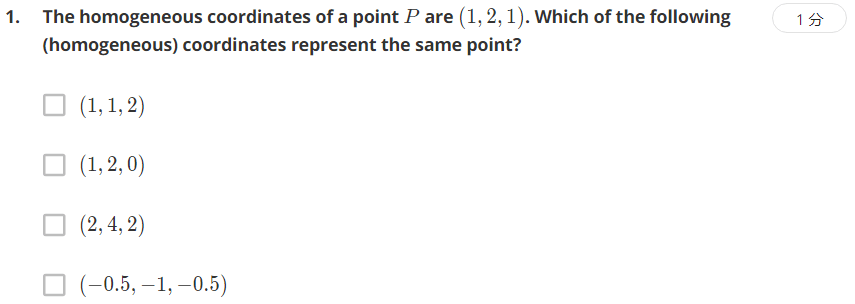 选C和D,考察齐次坐标的表示。成比例缩放。
选C和D,考察齐次坐标的表示。成比例缩放。
 根据题目ABCD是一个正方形,所以很容易得到B、D的齐次坐标分别是(1,0,1)、(0,1,1)。求过它们两点的直线,对其做叉乘即可。答案选A。
根据题目ABCD是一个正方形,所以很容易得到B、D的齐次坐标分别是(1,0,1)、(0,1,1)。求过它们两点的直线,对其做叉乘即可。答案选A。
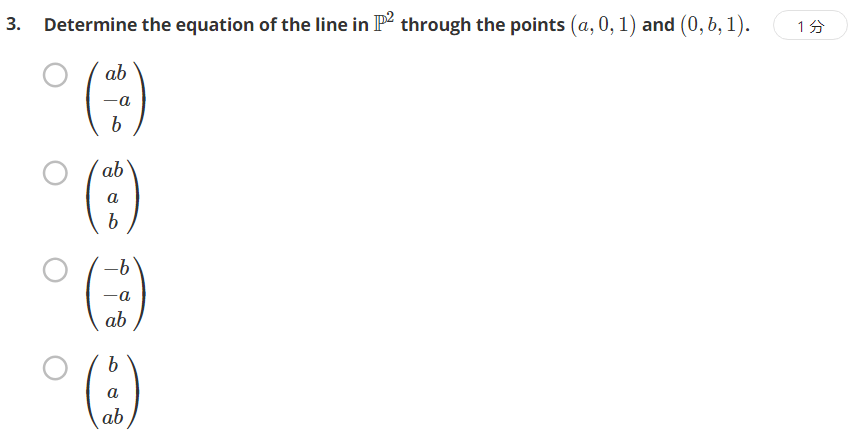 还是考察齐次坐标系下直线求法,直接对两点齐次坐标做叉乘即可。答案选C。
还是考察齐次坐标系下直线求法,直接对两点齐次坐标做叉乘即可。答案选C。
 做叉乘,答案选C。
做叉乘,答案选C。
 叉乘,答案选D。
叉乘,答案选D。
2.Projective Transformation
 至少需要4个点。
至少需要4个点。
 答案选D。根据课上介绍的方法,取a为(1,0,0),b为(0,1,0),c为(0,0,1)(坐标原点的齐次表示)。所以有(2,1,1)T=(αa,βb,γc)(1,1,1)T。这样就可以解出α、β、γ分别是2、1、1,再将α、β、γ带回,就可以得到变换矩阵了。
答案选D。根据课上介绍的方法,取a为(1,0,0),b为(0,1,0),c为(0,0,1)(坐标原点的齐次表示)。所以有(2,1,1)T=(αa,βb,γc)(1,1,1)T。这样就可以解出α、β、γ分别是2、1、1,再将α、β、γ带回,就可以得到变换矩阵了。
 答案选D。取a为(1,0,1),b为(0,1,1),c为(0,0,1),d为(1,1,1)。按照上述方法计算。这里题目对应的变换是从像平面到真实世界的变换。
答案选D。取a为(1,0,1),b为(0,1,1),c为(0,0,1),d为(1,1,1)。按照上述方法计算。这里题目对应的变换是从像平面到真实世界的变换。
 答案选C。
答案选C。
3.Vanishing Points
 选Yes。
选Yes。
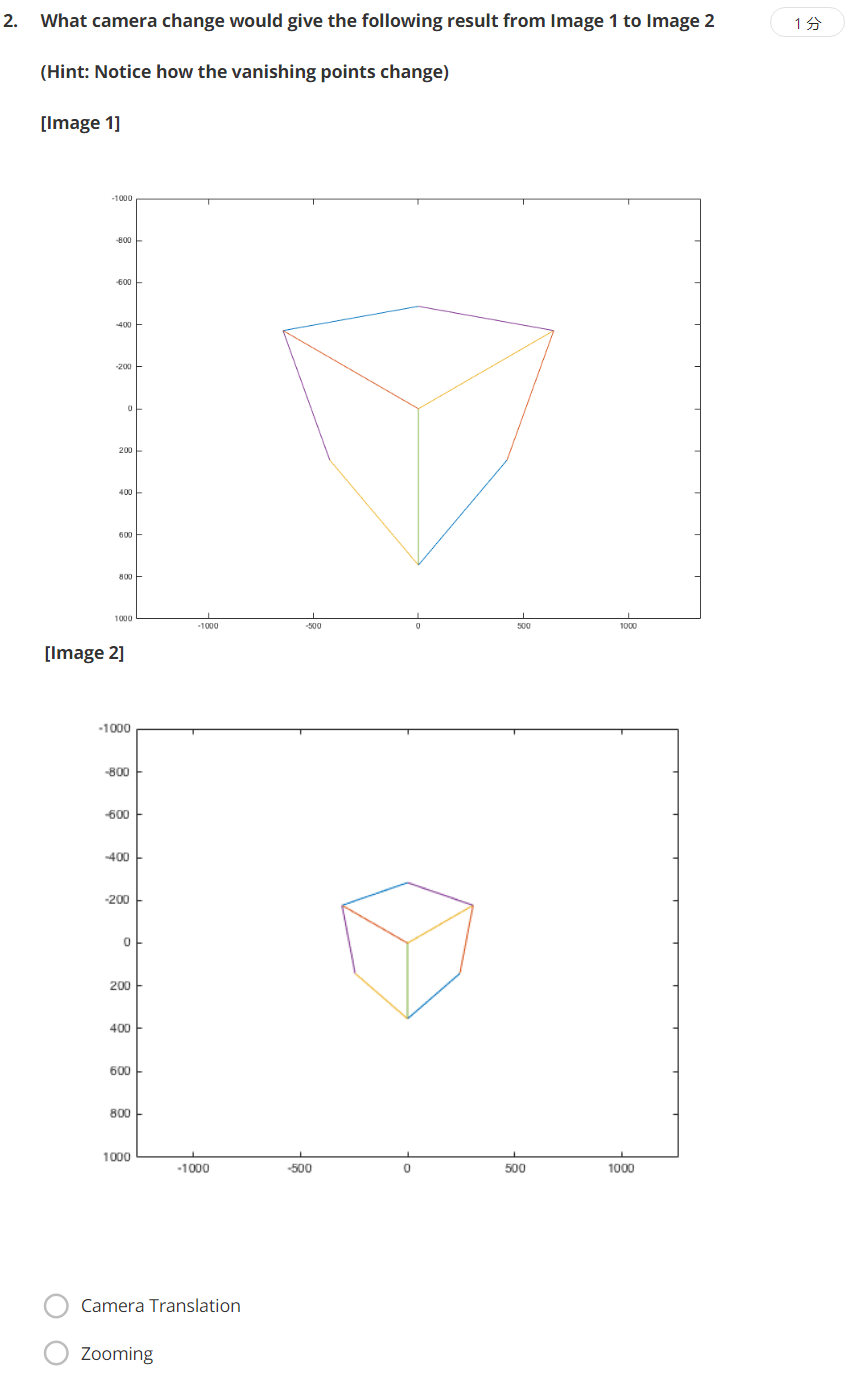 选Camera Translation。物体等比例缩放,所以是相机远离物体了。
选Camera Translation。物体等比例缩放,所以是相机远离物体了。
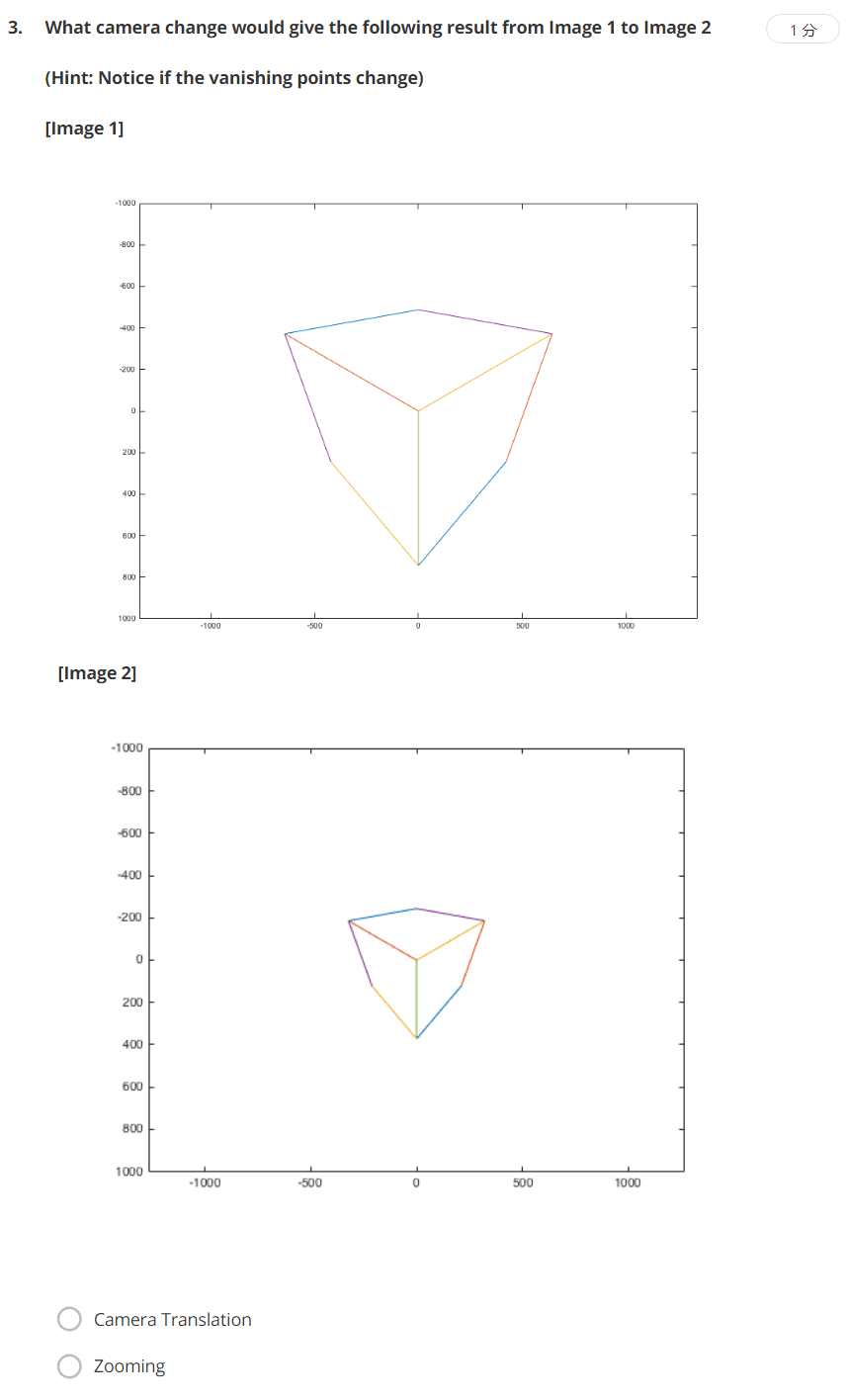 选Zooming。缩放会改变焦距与视角。
选Zooming。缩放会改变焦距与视角。
 选B。
选B。
4.Cross Ratios and Single View Metrology
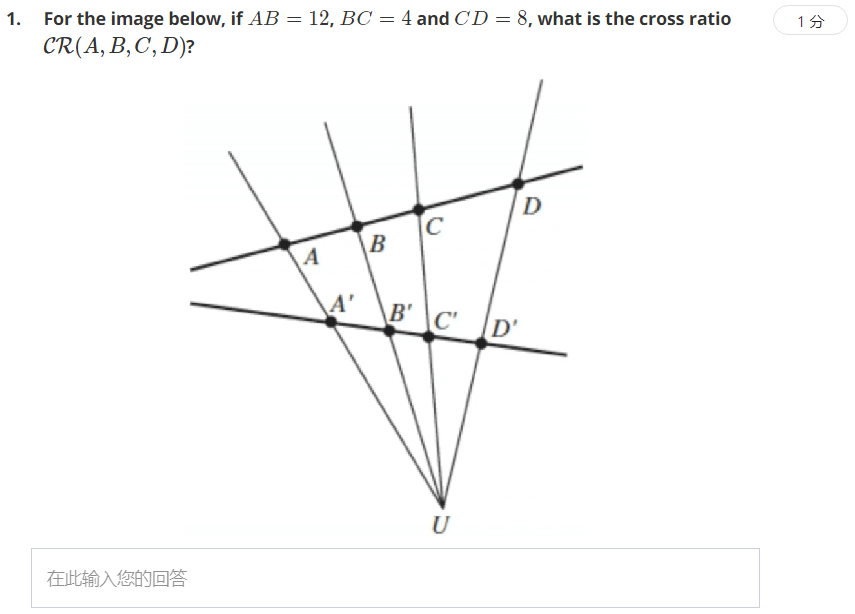 考察交比计算:(AC/AD):(BC/BD)计算结果为2。
考察交比计算:(AC/AD):(BC/BD)计算结果为2。
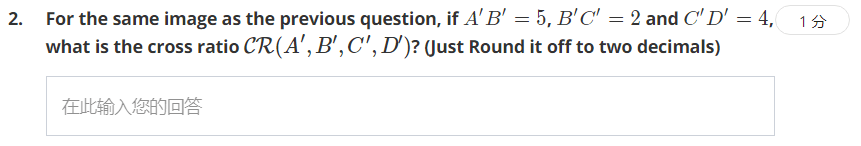 还是交比计算公式,计算结果为1.91,保留2位小数。
还是交比计算公式,计算结果为1.91,保留2位小数。
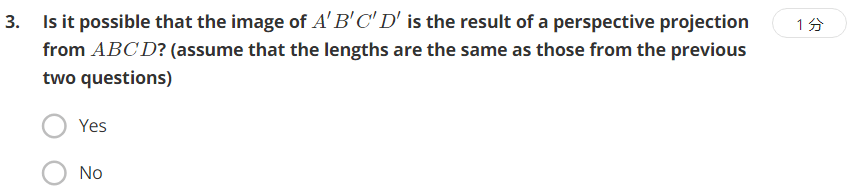 选No。因为交比数值不同。
选No。因为交比数值不同。
 要想它们满足投影关系,交比应相等,都为2,带入交比计算公式可以算得A’B’应该为6。
要想它们满足投影关系,交比应相等,都为2,带入交比计算公式可以算得A’B’应该为6。
5.Assignment-Image Projection using Homographies
利用单应矩阵实现虚拟广告板效果。题目与说明点击这里下载,提取码:xr53。最终实现效果如下:
 在作业中,需要修改的是
在作业中,需要修改的是est_homography.m和warp_pts.m这两个文件,它们分别用于求取坐标点之间的单应变换矩阵,以及根据单应矩阵对坐标点进行变换。
在求解单应矩阵时,按照PDF中的公式(13)、(14)、(15)展开成Ah=0的形式即可。注意公式(14)中不知从哪里冒出来个x3,这是错的,这个地方应该为0。在得到Ah=0的形式后就可以直接用SVD分解来做了,方程的解就是分解得到的V矩阵的最右边一列。注意最右边一列与未知量h的对应关系,前三个元素对应H矩阵的第一行h11、h12、h13,以此类推。千万别弄反了!如果使用Matlab的reshape函数对向量进行拆分,需要注意的是它默认是按列对向量进行拆分的,这样直接得到的H矩阵的第一行元素就是h11、h21、h31,显然是不对的了。所以在reshape后需要对得到的H矩阵转置,才是我们想要的结果。如果不想用reshape函数,手动构造也是完全可以的。
而对于根据单应矩阵进行坐标变换时建议直接用矩阵运算进行操作,不推荐利用for循环将输入的待采样点逐个遍历,因为经过测试发现会非常慢。我们可以先对输入的n×2的待采样点转置,得到2×n的矩阵,然后在其末尾添加一行写成齐次坐标,变成3×n。这样我们就可以直接拿得到的单应矩阵H与它相乘了,乘完之后可以得到3×n大小的结果,所以转置下变成n×3。由于我们需要的是像面上的齐次坐标,所以对每一行都除以z分量,这个步骤可以用for循环来做,这样矩阵的最后一列全部变成1了。最后只取矩阵的前两列即可得到n×2的结果。
除此之外作业中还有两个需要注意和学习的地方:
1.在PDF中为什么求取的是视频坐标到LOGO坐标的“反变换”。根据我们的需求应该是寻找一个变换使得LOGO变换到视频上。原因在PDF中也进行了说明,这里再提一下。简单来说就是为了防止LOGO变换到视频中后有些像素出现“空洞”。如果我们采用LOGO到视频的变换,由于像素的取整等因素影响,很有可能出现LOGO中的多个像素变换到视频中同一个点的情况,而其它地方可能没有对应值。基于这种考虑采用了反变换,将视频中的像素点变换到LOGO中,并获取对应位置上的灰度。由于变换后的点肯定在LOGO影像内,所以肯定能取到值,不会出现空洞情况,宁可重复也不能遗漏,类似于“查询检索”。这种在实际应用中的小技巧值得学习。
2.在一开始写的时候,在结算单应矩阵时利用reshape函数重构得到H后并没有对H进行转置,但最后算得的结果是对的,评分也是100分。所以不需要对reshape求得的H转置吗?答案当然是否定的。后来检查了代码才发现,之所以出现这种情况是因为“错错得对”。我在求解单应矩阵的时候没有转置,相当于是真实H的转置。我在坐标变换的时候写的代码是warped_pts = sample_pts*H;,可以看到H乘错地方了。但正是因为H乘到了右边,反而导致了没有转置的H对了。原因也很简单,正确的顺序应该是warped_pts = H*sample_pts;,如果同时对等式两边取转置,根据转置法则,右边就变成了sample_pts^T*H^T。注意这里的H是正确的H,而H^T恰恰就是我们利用reshape求得且没转置的单应矩阵。而sample_pts虽然输入的是n×2,但是可以这样理解:一般坐标习惯上应该写成2×n形式,再添加一维写成齐次,应该为3×n。这里对一个3×n的sample_pts进行了转置,得到了n×3(也就是齐次形式的函数的输入),并与3×3的未转置的单应矩阵相乘,反而得到了正确的结果。这个错误比较隐蔽,是在做第三周的作业时发现的。
完整写好的代码点击这里下载,提取码:lmto。
本文作者原创,未经许可不得转载,谢谢配合
