本篇博客对应旷视CV Master训练营《计算摄影学》专题第三次课,课程视频可以点此查看。笔记在课程内容的基础上加入了一些自己的理解,不一定完全正确,欢迎互相交流。本次课程的主要内容是计算摄影中的模型设计。

1.计算摄影中的模型设计
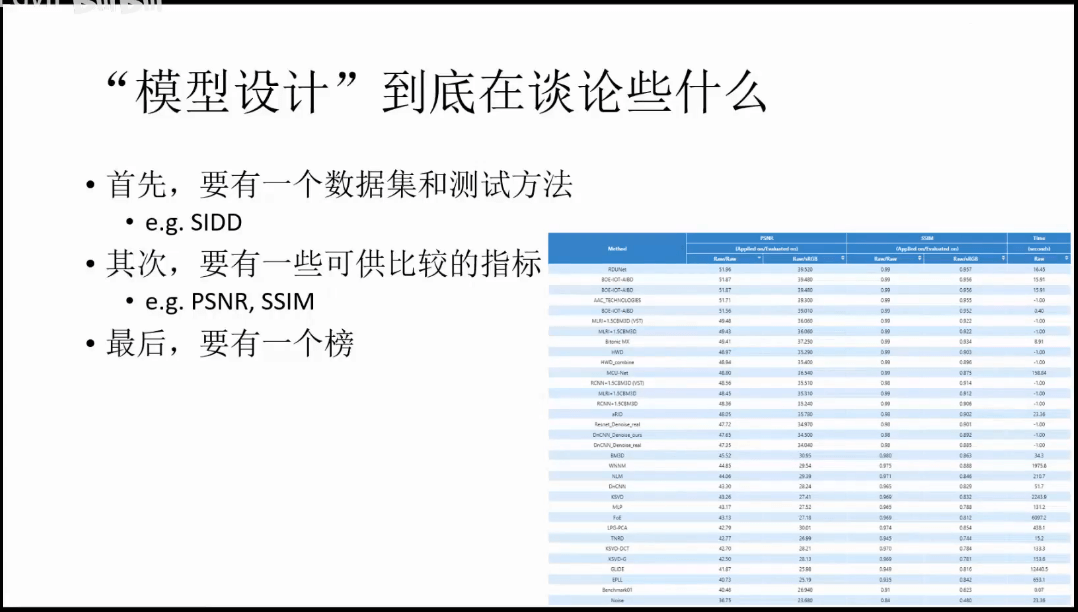 模型设计至少应该包含以下几个方面:第一是公开的数据集和测试方法,第二是可供比较的评价指标,第三是一个排行榜,汇总最新成果。这里提到了指标相关的内容,就简单介绍一下三个常用的图像质量评价指标:MSE、PSNR和SSIM。
模型设计至少应该包含以下几个方面:第一是公开的数据集和测试方法,第二是可供比较的评价指标,第三是一个排行榜,汇总最新成果。这里提到了指标相关的内容,就简单介绍一下三个常用的图像质量评价指标:MSE、PSNR和SSIM。
(1)图像质量评价指标MSE
MSE是Mean Square Error的缩写,中文叫均方误差。对于某个目标影像\(I\),我们有估计的影像\(K\)。我们可以逐像素的计算两者之间的误差,然后求均值,即作为衡量两个影像相似度的指标,如下图所示。
\[MSE = \frac{1}{mn}\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}(I(i,j)-K(i,j))^2\]如果我们以某个完美的影像作为比较对象,那么估计的影像和它越相似,则说明质量越好,这是非常好理解的。对于RGB彩色影像,我们可以分别计算每个波段的MSE,然后求平均作为整个彩色图像的MSE。或者先把RGB转换成灰度图像,然后求MSE。
(2)图像质量评价指标PSNR
PSNR是Peak Signal-toNoise Ratio的缩写,中文翻译为峰值信噪比。有了上面的MSE计算公式,PSNR就可以很容易得到,如下。
\[PSNR = 10 \cdot log_{10}(\frac{MAX^2}{MSE})\]这里,\(MAX\)表示图像可能的最大像素值,比如8bit影像最大值就为255,对于浮点型数据,最大值为1。可以看出,这里为了表示方便,取了对数,也就是以分贝(dB)的形式表示的。这里需要注意一下,分贝(dB)是一个纯计数单位,是两种信号的比值,而非一个物理单位。通用的分贝(dB)计算公式如下。
\[dB = 10 log(\frac{A}{B})\]这就表示A、B两个信号的比值然后取对数。同时,由于是比值,所以就把物理量的量纲给消去了,所以说是一个计数单位。对于RGB彩色影像,我们可以有三个计算方式:
- (1)计算RGB三通道每个通道的PSNR值,然后再求平均作为图像的PSNR
- (2)计算RGB三通道每个通道的MSE值,再求平均,得到平均MSE,然后用这个平均MSE求解PSNR
- (3)将RGB转换为YUV空间,仅仅计算Y分量的PSNR作为整个图像的PSNR
这其中,方法2和3用的比较多,方法1不太常用。
(3)图像质量评价指标SSIM
SSIM是Structural Similarity的缩写,中文为结构相似性。一般而言,比较亮度(Illumination)、对比度(Contrast)和结构(Structure)三个方面的差异。对于图像中的某个位置\((x,y)\),我们可以分别列出计算公式,如下。
\[l(x,y)=\frac{2\mu_{x}\mu_{y}+c_{1}}{\mu_{x}^{2}\mu_{y}^{2}+c_{1}}\] \[c(x,y)=\frac{2\sigma_{x}\sigma_{y}+c_{2}}{\sigma_{x}^{2}\sigma_{y}^{2}+c_{2}}\] \[s(x,y)=\frac{\sigma_{xy}+c_{3}}{\sigma_{x}\sigma_{y}+c_{3}}\]这其中:
- \(\mu_{x}\)为\(x\)的均值
- \(\mu_{y}\)为\(y\)的均值
- \(\sigma_{x}^{2}\)为\(x\)的方差
- \(\sigma_{y}^{2}\)为\(y\)的方差
- \(\sigma_{xy}\)为\(x\)和\(y\)的协方差
- \(c_{1}=(k_{1}L)^{2},c_{2}=(k_{2}L)^{2}\)为两个常数,避免除0
- \(L\)为像素值范围,等于\(2^{B}-1\)
- \(k_{1}=0.01,k_{2}=0.03\)为默认值
有了以上的定义,SSIM可以按下式计算:
\[SSIM(x,y)=[l(x,y)^{\alpha} \cdot c(x,y)^{\beta} \cdot s(x,y)^{\gamma}]\]如果我们把\(\alpha,\beta,\gamma\)都设为1,那么再将上面的式子整理、合并,可以得到下式。
\[SSIM(x,y)=\frac{(2\mu_{x}\mu_{y}+c_{1})(2\sigma_{xy}+c_{2})}{(\mu_{x}^{2}+\mu_{y}^{2}+c_{1})(\sigma_{x}^{2}+\sigma_{y}^{2}+c_{2})}\]在实际计算时,从图像上取\(N \times N\)的窗口,不断滑动窗口计算,可以得到每个位置上的SSIM。最后,再将所有的SSIM值求平均,其就作为整张影像的SSIM。如果图像有多个波段,我们可以每个波段都计算一个SSIM,最后所有波段求平均,得到MSSIM。
2.模型训练的一般过程
 模型的大概训练流程如图所示,可以分为四步。第一步是获取数据,得到输入影像和真值。第二步是将配对数据传入网络,得到估计值。第三步是计算估计值与真值之间的误差。第四步是将这个误差再反向传播回去,以修正参数,获得更好结果。可以看到,对于计算摄影的网络而言,网络的输入和输出影像的维度是不变的。这点和分类或者目标识别网络有所不同。
模型的大概训练流程如图所示,可以分为四步。第一步是获取数据,得到输入影像和真值。第二步是将配对数据传入网络,得到估计值。第三步是计算估计值与真值之间的误差。第四步是将这个误差再反向传播回去,以修正参数,获得更好结果。可以看到,对于计算摄影的网络而言,网络的输入和输出影像的维度是不变的。这点和分类或者目标识别网络有所不同。
3.经典影像去噪模型
(1)开宗立派DnCNN
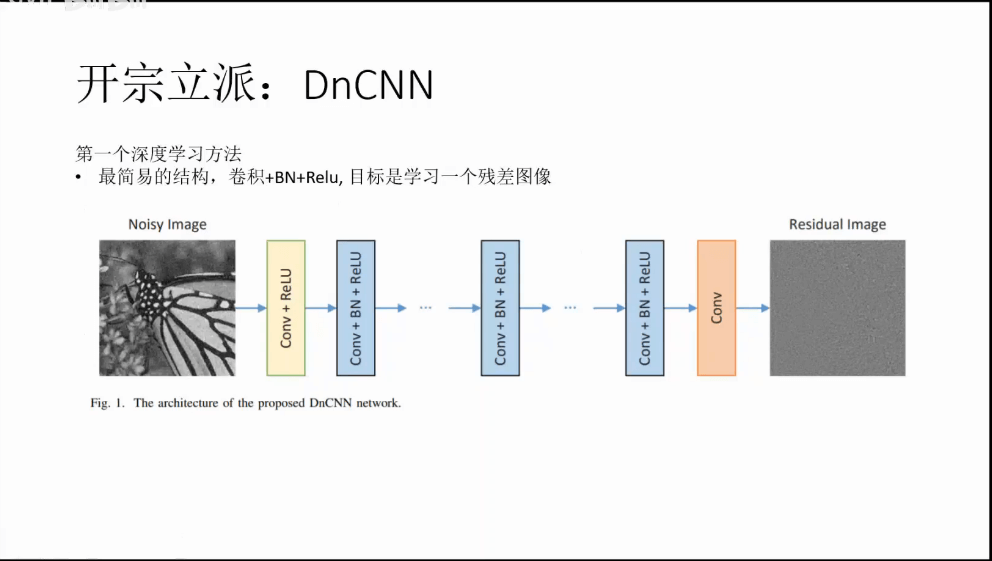

 从上图中可以看到,最左边的MLP比旁边的TNRD小了只有0.05个dB,但是可视效果上来说就能看出明显的差别了。所以对于PSNR这个指标而言,数值上轻微的变化可能就对应了实际效果上的巨大差异。
从上图中可以看到,最左边的MLP比旁边的TNRD小了只有0.05个dB,但是可视效果上来说就能看出明显的差别了。所以对于PSNR这个指标而言,数值上轻微的变化可能就对应了实际效果上的巨大差异。

(2)不同的方向
 从神经网络诞生,其实就可以划分为两个方向,一个方向是追求更强,即通过更复杂的网络结构、更强的硬件实现性能的提升,不关注运行效率;另一个方向是追求更快,即在相同或相似的性能下,把计算量降到最小。
从神经网络诞生,其实就可以划分为两个方向,一个方向是追求更强,即通过更复杂的网络结构、更强的硬件实现性能的提升,不关注运行效率;另一个方向是追求更快,即在相同或相似的性能下,把计算量降到最小。
(3)更复杂的网络结构
a.残差
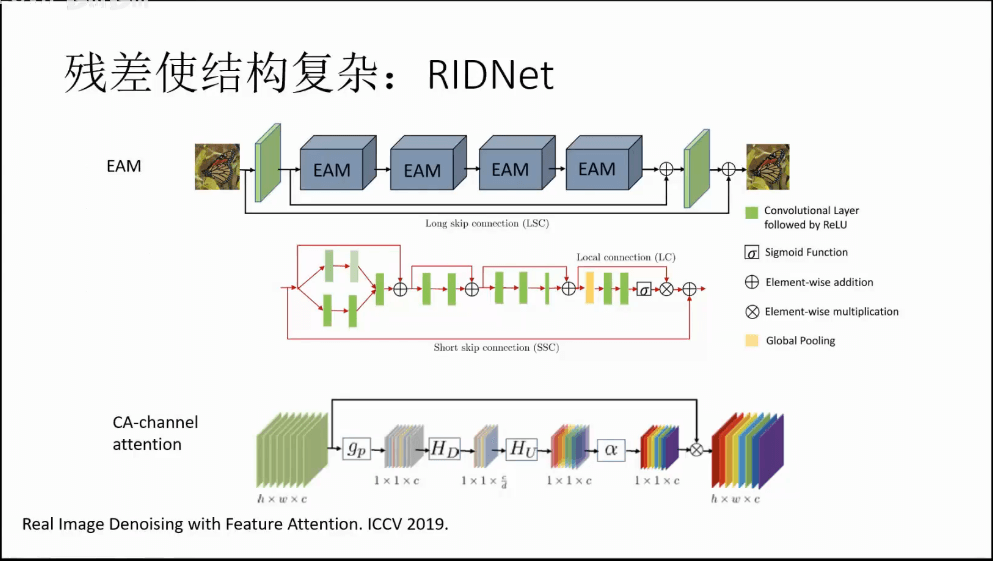 残差结构使得网络结构更加复杂。
残差结构使得网络结构更加复杂。
 如上图所示,可以看到,降噪类问题天生适合“残差”的定义。所谓残差,上图其实说的很明白了,简单来说就是我们不仅仅获取输出的结果,还有输入的结果。比如对于输入的x,我们首先将其赋给x0,然后把x输入网络,经过一系列操作,得到结果y。而最后我们的最终结果是y+x0,而不是单纯的y。这样做有一个好处就是,设想一个极端情况,就是网络什么都没干,输出为0。那么此时我们得到的输出就等于x0,也就是和原始输入一样。
如上图所示,可以看到,降噪类问题天生适合“残差”的定义。所谓残差,上图其实说的很明白了,简单来说就是我们不仅仅获取输出的结果,还有输入的结果。比如对于输入的x,我们首先将其赋给x0,然后把x输入网络,经过一系列操作,得到结果y。而最后我们的最终结果是y+x0,而不是单纯的y。这样做有一个好处就是,设想一个极端情况,就是网络什么都没干,输出为0。那么此时我们得到的输出就等于x0,也就是和原始输入一样。
b.Batch Normalization
 对于一些检测或者识别的任务,BN可能是必须的操作和模块。但对于降噪问题而言,用不用BN就是一个问题。通过BN,可以归一化输入数据,使得训练相对稳定。但是坏处就是其网络输出会依赖同batch的其它图片。这种不稳定或者说结果的抖动对于分类或者识别任务影响可能不会很明显,比如只要大于某个阈值,不管是0.9还是0.999,都认为是某一类物体。但对于图像处理这类任务,这种抖动就是比较麻烦了。比如我们好不容易降了噪声灰度变成128,因为抖动下次又变成129了,这种差异显然是不能接受的。所以在做图像处理相关任务的时候,我们一般不使用BN,以此规避一些可能的问题。
对于一些检测或者识别的任务,BN可能是必须的操作和模块。但对于降噪问题而言,用不用BN就是一个问题。通过BN,可以归一化输入数据,使得训练相对稳定。但是坏处就是其网络输出会依赖同batch的其它图片。这种不稳定或者说结果的抖动对于分类或者识别任务影响可能不会很明显,比如只要大于某个阈值,不管是0.9还是0.999,都认为是某一类物体。但对于图像处理这类任务,这种抖动就是比较麻烦了。比如我们好不容易降了噪声灰度变成128,因为抖动下次又变成129了,这种差异显然是不能接受的。所以在做图像处理相关任务的时候,我们一般不使用BN,以此规避一些可能的问题。
而如果真的要用BN,那么可以将BN与residual联动,如下图所示。

c.MIRNet
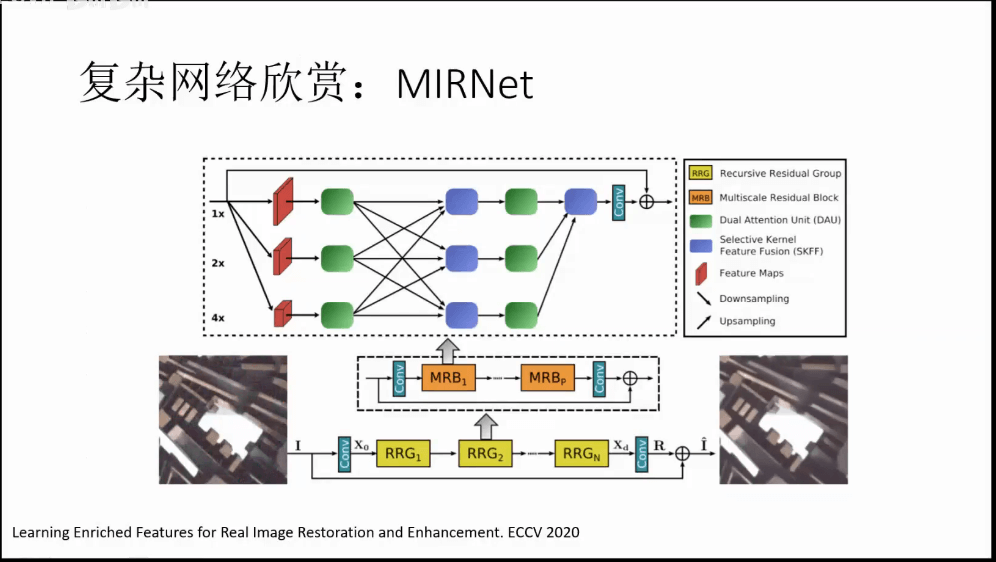
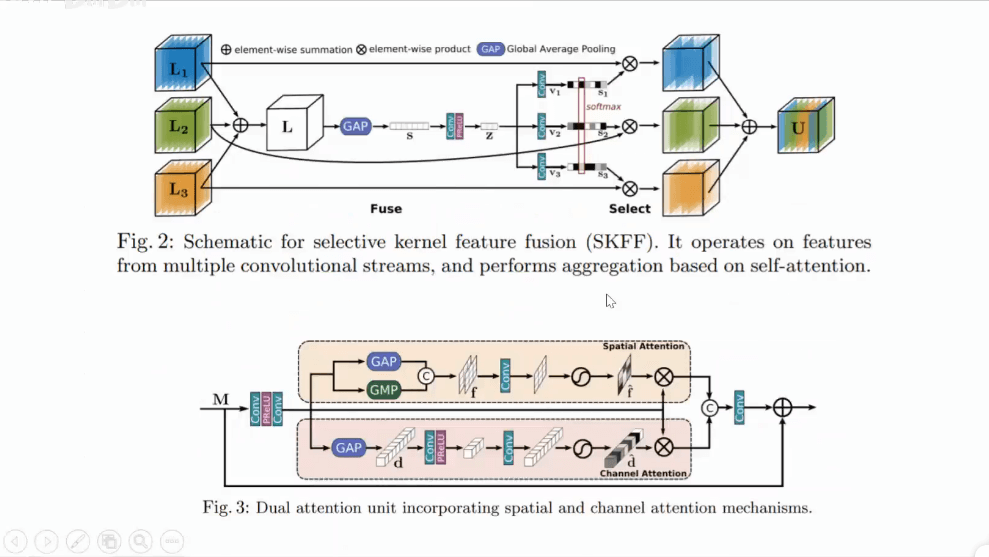
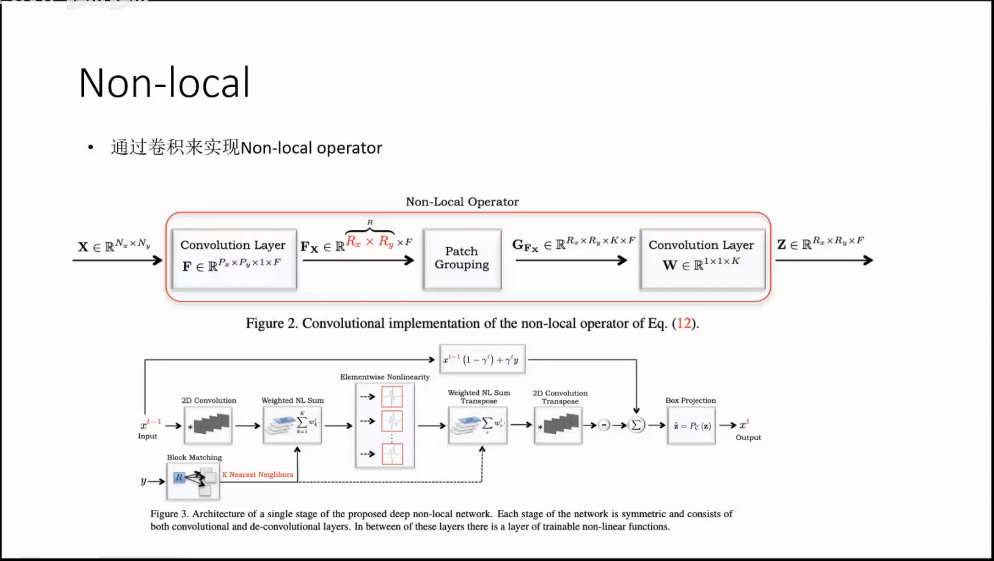
其它一些结构。
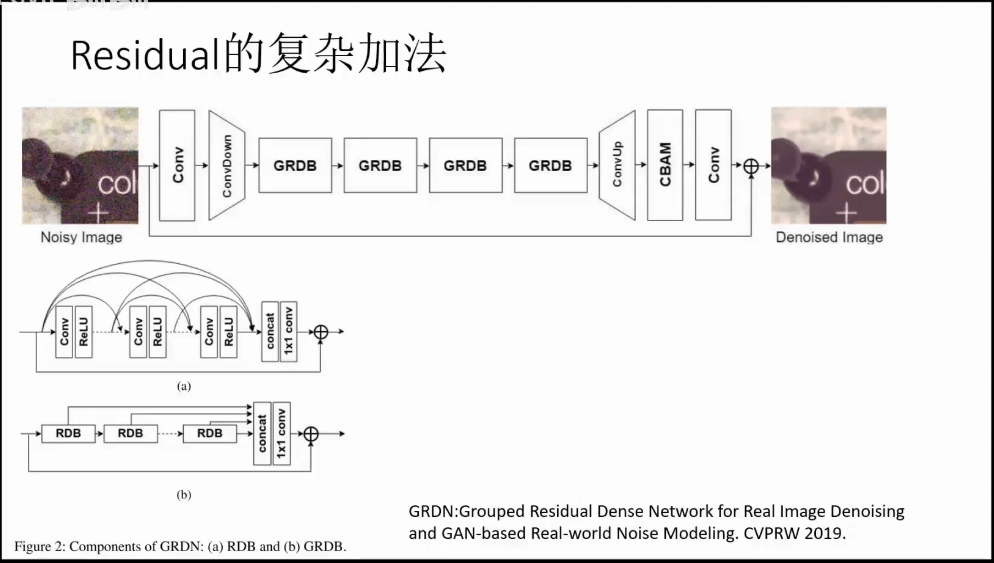
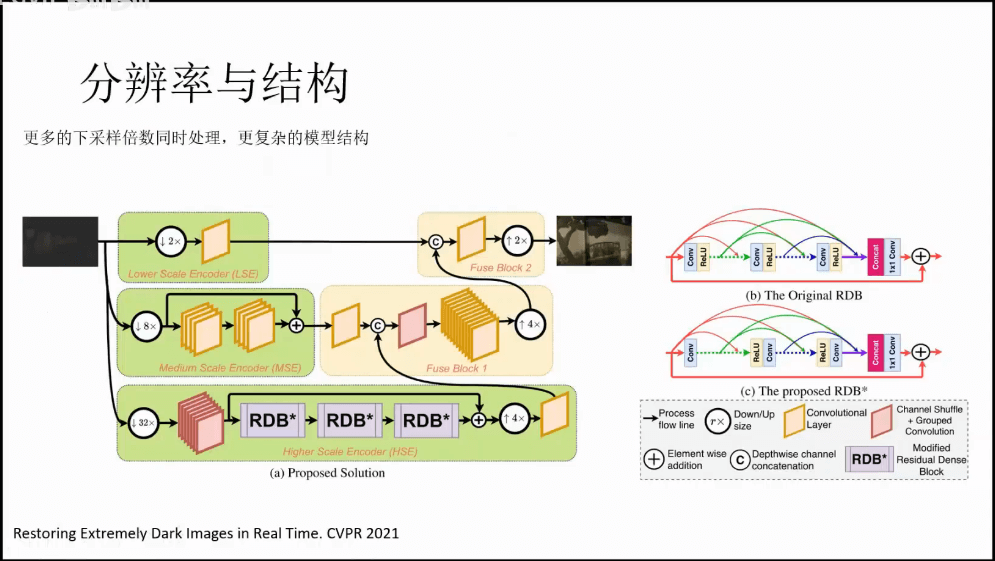
(4)更少的计算量
a.NBNet
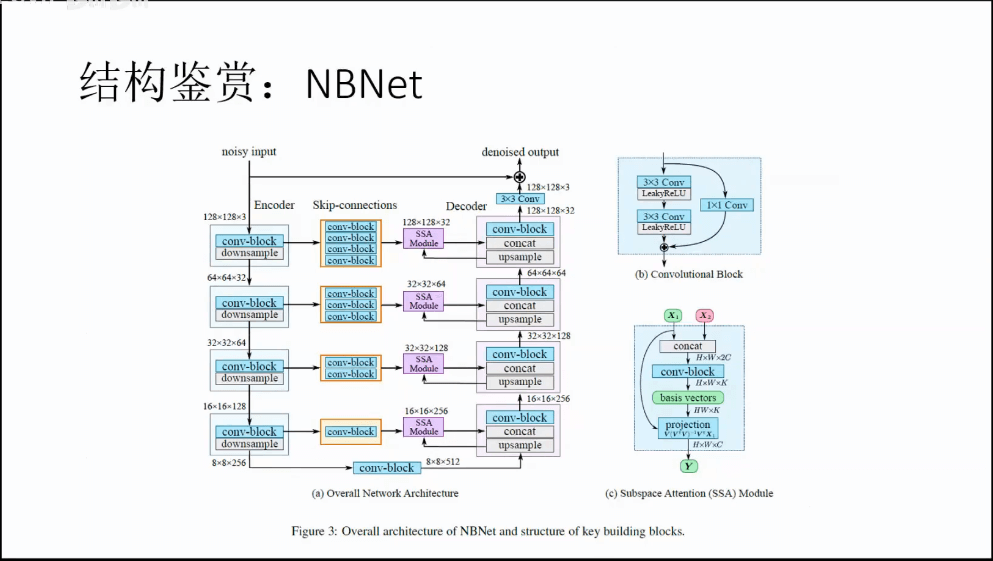

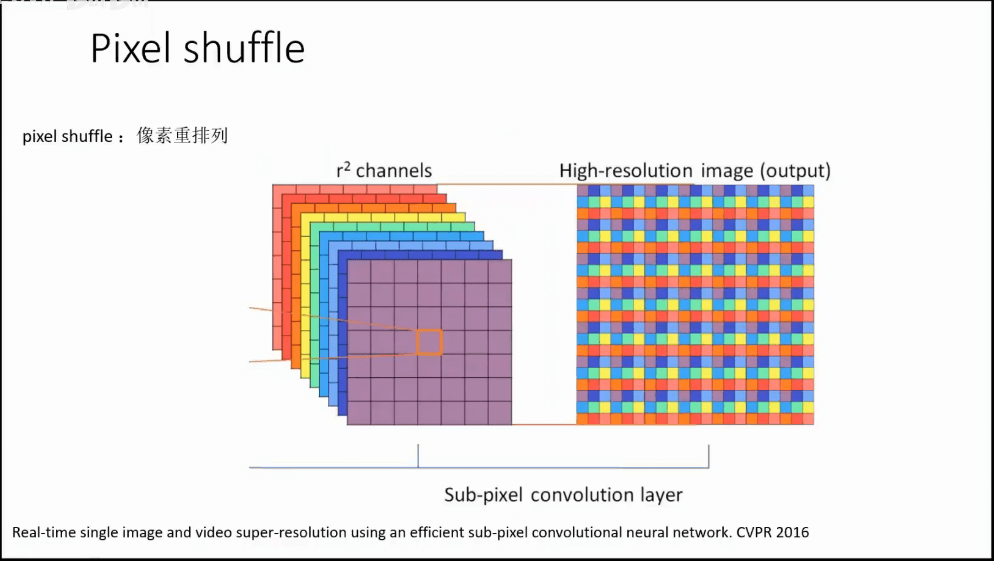
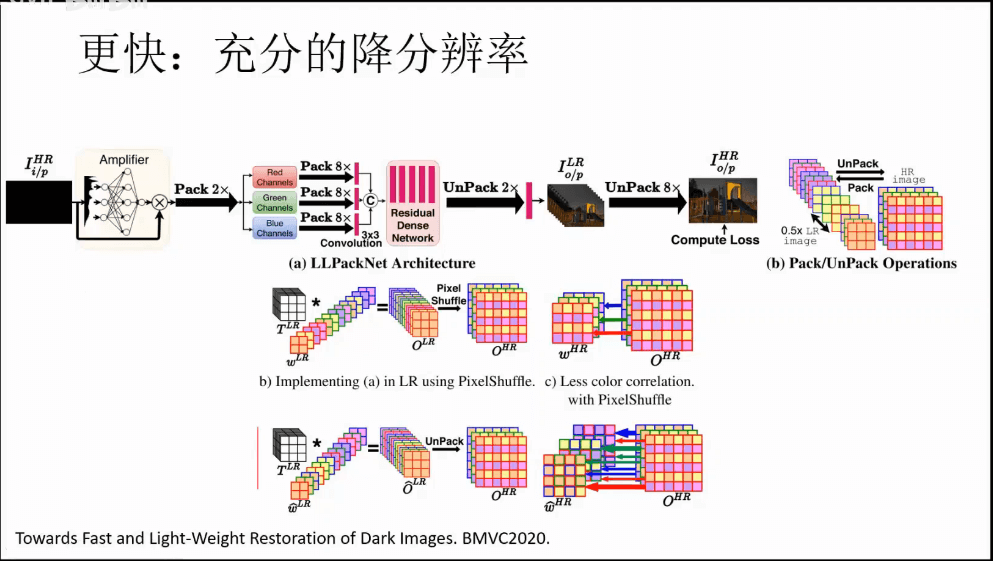
b.其它一些技巧



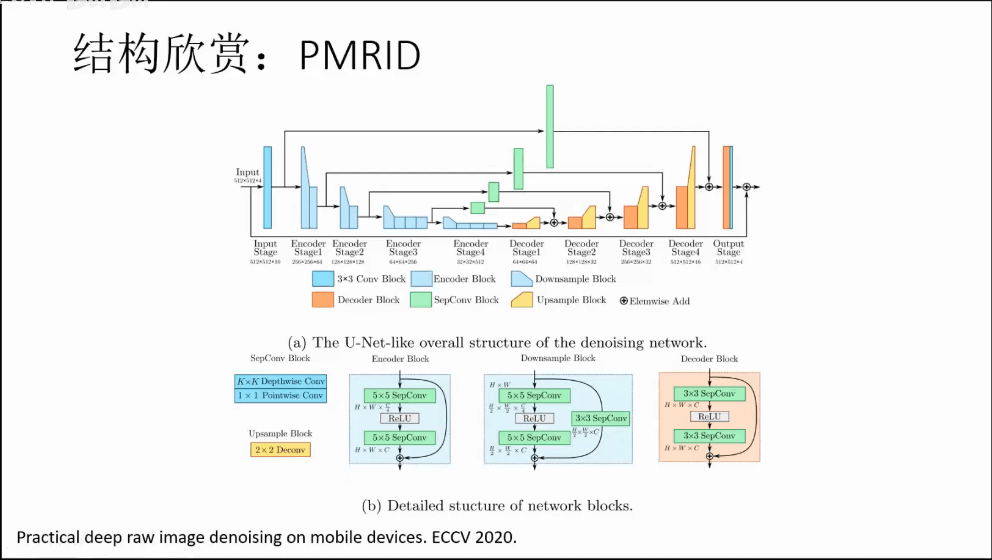
c.PMRID

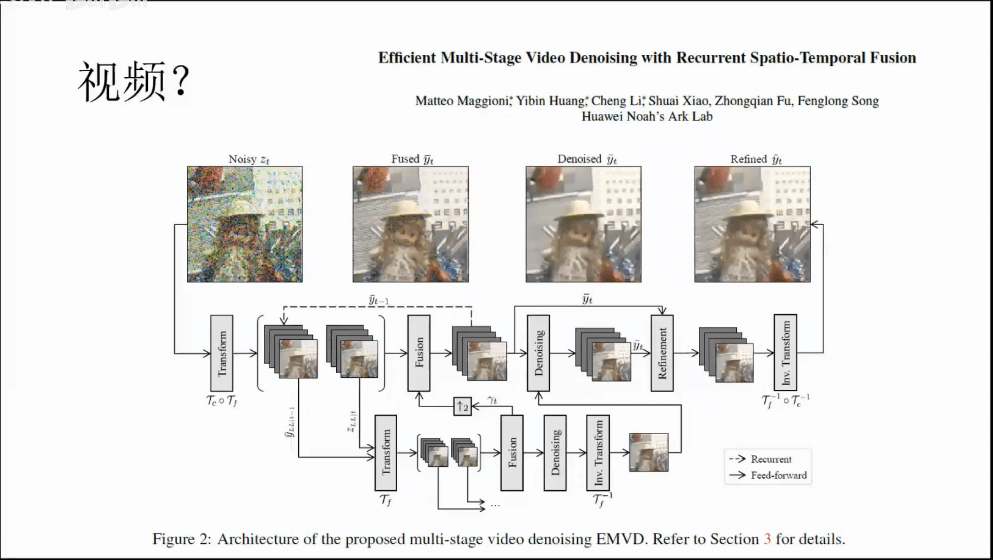
4.视频去噪

5.超分辨率
 很多网络结构都是相似的,可能去噪效果好的网络,稍微改改也适合于超分辨率。
很多网络结构都是相似的,可能去噪效果好的网络,稍微改改也适合于超分辨率。
6.作业

7.参考资料
- [1]https://zhuanlan.zhihu.com/p/50757421
- [2]https://blog.csdn.net/edogawachia/article/details/78756680
- [3]https://www.zhihu.com/question/21743572
本文作者原创,未经许可不得转载,谢谢配合
