IMU与惯性导航基础知识介绍

• 1.惯性导航(Inertial Navigation)
  • 1.1 惯性系统的配置
    • 1.1.1 平台系统
    • 1.1.2 捷联系统
• 2.陀螺仪基本介绍(Gyroscope)
  • 2.1 陀螺仪的种类
    • 2.1.1 机械式(Mechanical)
    • 2.1.2 光纤式(Optical)
    • 2.1.3 微机电式(MEMS)
  • 2.2 MEMS陀螺仪的误差特性
    • 2.2.1 常量偏置(Constant Bias)
    • 2.2.2 热机械白噪声/角度随机游走(Thermo-Mechanical White Noise/Angle Random Walk)
    • 2.2.3 闪变噪声/偏置稳定性(Flicker Noise/Bias Stability)
    • 2.2.4 温度影响(Temperature Effects)
    • 2.2.5 校正误差(Calibration Errors)
    • 2.2.6 小节
• 3.线性加速度计基本介绍(Linear Accelerometer)
  • 3.1 加速度计的种类
    • 3.1.1 机械式
    • 3.1.2 固态
    • 3.1.3 MEMS
  • 3.2 MEMS加速度计的误差特性
    • 3.2.1 常量偏置(Constant Bias)
    • 3.2.2 热机械白噪声/速度随机游走(Thermo-Mechanical White Noise/Velocity Random Walk)
    • 3.2.3 闪变噪声/偏置稳定性(Flicker Noise/Bias Stability)
    • 3.2.4 温度影响(Temperature Effects)
    • 3.2.5 校正误差(Calibration Errors)
    • 3.2.6 小节
• 4.捷联惯性导航
  • 4.1 推算姿态
    • 4.1.1 理论
    • 4.1.2 实现
    • 4.1.3 误差
  • 4.2 推算位置
    • 4.2.1 理论
    • 4.2.2 实现
    • 4.2.3 误差
• 5.参考资料

本篇博客是剑桥大学2007年的一篇技术报告《An Introduction to Inertial Navigation》(作者Oliver J. Woodman)的阅读笔记，这篇报告介绍了IMU相关的基础知识。由于是阅读笔记，所以记录了一些我认为比较重要的知识点，但不一定很有逻辑性和完整性。如果感兴趣可以点击这里查看技术报告原文，获得最完整的阅读体验。

1.惯性导航(Inertial Navigation)

惯性导航(Inertial Navigation)是一种独立于外部的(self-contained)的导航技术，它使用加速度计(accelerometer)和陀螺仪(gyroscope)来追踪物体相对于某个已知的状态(位置、方向与速度)的位置和方向。这是对于惯性导航的基本定义。在惯性导航中，无法回避的传感器自然就是惯性测量单元(IMU)。惯性测量单元(Inertial Measurement Unit, IMU)通常包含三个互相垂直的速率陀螺仪(rate-gyroscpoe)以及三个互相垂直的加速度计(accelerometer)，分别用于测量角速度和线加速度。通过处理IMU的观测数据，就可以跟踪某个物体的位置与姿态，这也就是惯性导航的过程。惯导的观测由于不需要依赖于外部环境，所以应用很广，当然一个典型的应用就是在巡航导弹上。

1.1 惯性系统的配置

通常而言，惯性系统有两种配置模式：平台系统(Stable Platform System)和捷联系统(Strapdown System)。这两种配置模式最大的区别就是陀螺仪和加速度计的参考系不同(后面会详细介绍)。一个典型的惯导系统会涉及本体坐标系(Body Frame)和全局坐标系(Global Frame)，如下。

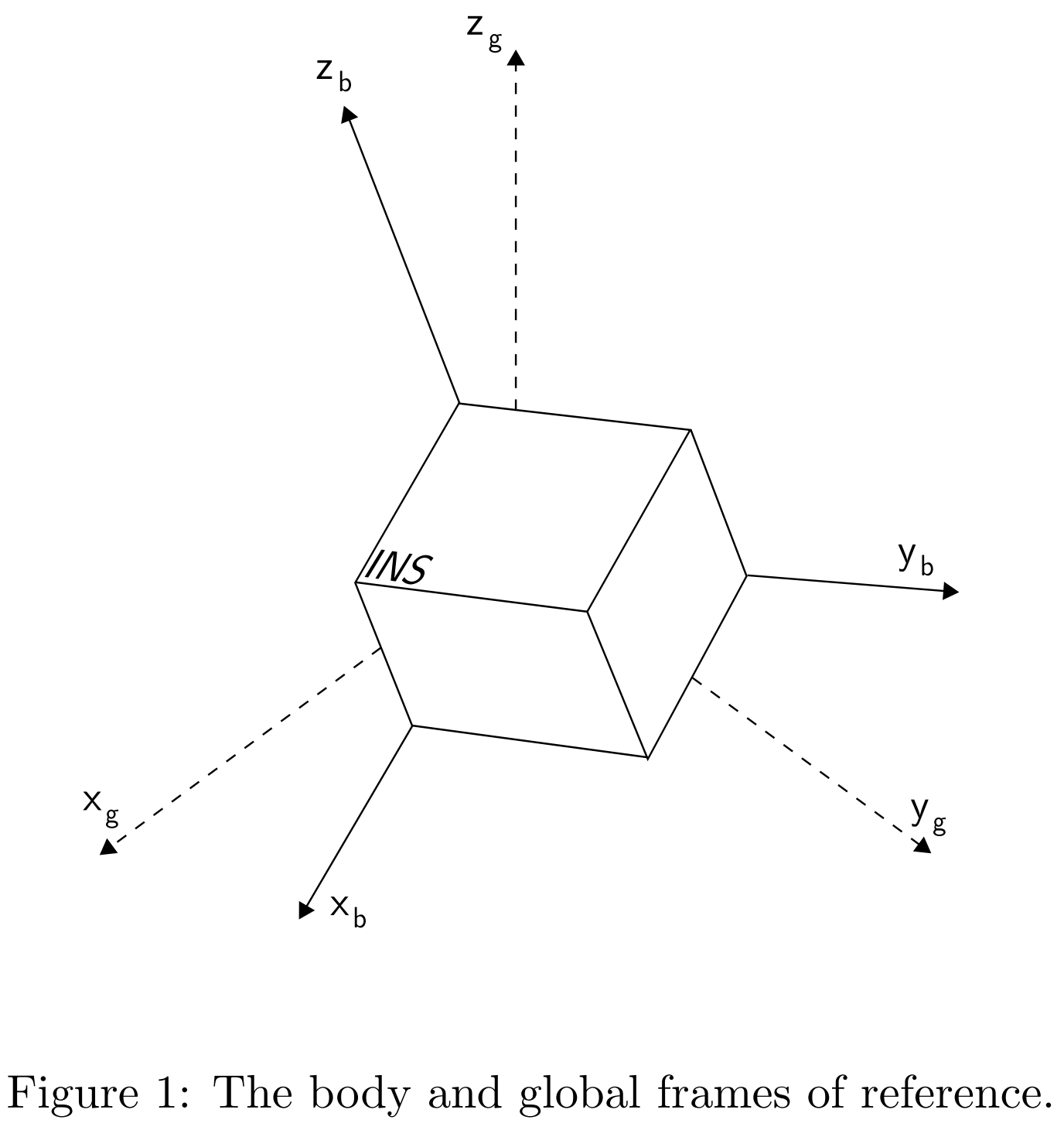
1.1.1 平台系统

在平台系统中，惯性传感器被放置在与外部旋转运动隔离的平台上(与运动物体非刚体连接)，换句话说，惯性传感器始终与全局坐标系对齐。说人话就是，惯性传感器被放置在一个与物体固联的云台上——随云台运动，但不随云台旋转。 如上图所示，为大疆Mavic Air无人机云台动图展示。可以看到相机不随无人机旋转。一个典型的云台(gimbal)示意图如下。 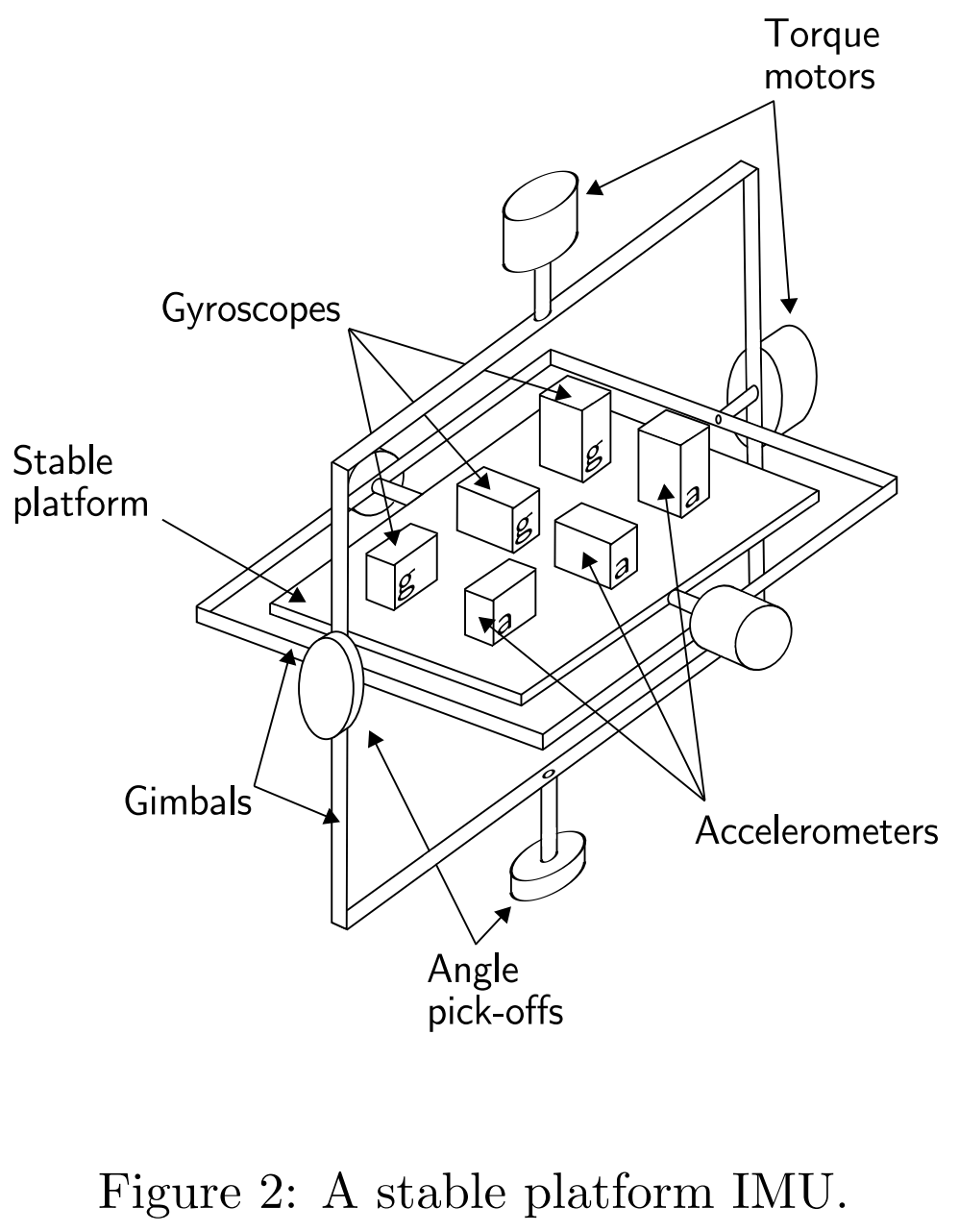板载陀螺仪检测平台的任意旋转，然后通过云台的马达调整消除，从而保证整体平台稳定，与全局坐标系对齐。

对于平台系统，我们可以通过读取两个时刻云台三轴刻度的差异来获取物体的旋转，比较容易理解。而对于位置，由于测量平台始终和全局坐标系对齐，所以加速度计观测的加速度也是全局坐标系下的加速度。根据高中物理的基本知识，对加速度积分两次即可得到位移(在全局坐标系下)。当然需要注意的是，由于存在重力，在对加速度计积分前需要先设法消除重力的影响。所以，一个稳定平台惯性导航算法应该如下。 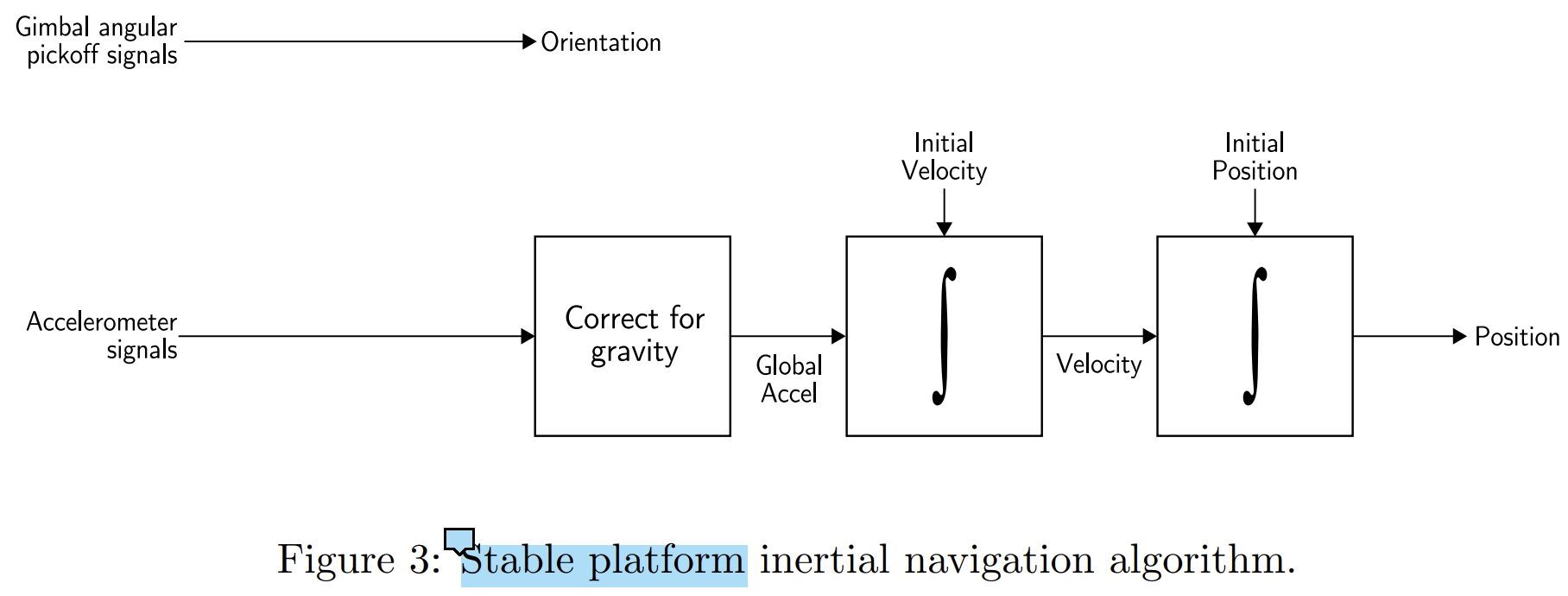可以看到，整体算法流程还是比较简单的。由于与全局坐标系对齐，甚至直接读取云台的刻度就可以获得物体的姿态。同样，得益于坐标系对齐，加速度积分过程也避免了坐标转换。

1.1.2 捷联系统

所谓捷联系统，英文为Strapdown System。Strapdown这个单词的原意为“捆绑”。所以捷联系统就是指将惯性传感器直接“捆绑”到运动平台上，而非像稳定平台系统一样把惯性传感器放到云台上。所以也可以看出来，捷联系统中惯性传感器和运动平台直接相连，运动过程中相对关系不会改变，为刚体连接(mounted rigidly)；稳定平台系统中惯性传感器和运动平台通过云台相连，运动过程中相对关系会改变，为非刚体连接。一个典型的无人机捷联系统如下。 可以看到，IMU被牢牢绑在无人机上，随无人机一起运动。这就是一个典型的捷联系统。通过上面的描述可以看出，捷联系统从成本和配置上是最方便的，直接把传感器往运动平台上一贴就完事了(方便，而且省了云台的钱)。捷联系统拥有更少的机械复杂性，并且在尺寸上也可以做的比平台系统更小。当然了，这样的代价就是计算复杂度增加了。但随着硬件的发展，计算能力越来越强，这个缺点也正慢慢被弥补，所以捷联系统也是在实际中被使用最多的系统。

对于捷联系统，需要注意的是所有的观测都是在本体坐标系下，而非全局坐标系。对于姿态，通过对陀螺仪的观测进行积分得到；对于位置，首先利用陀螺仪积分得到的姿态获得当前时刻本体坐标系相对于全局坐标系的变换，将加速度计的观测转换到全局坐标系下。在消除重力加速度影响后，对观测进行二次积分，最终即可得到全局坐标系下的位置。上述整体流程如下图所示。 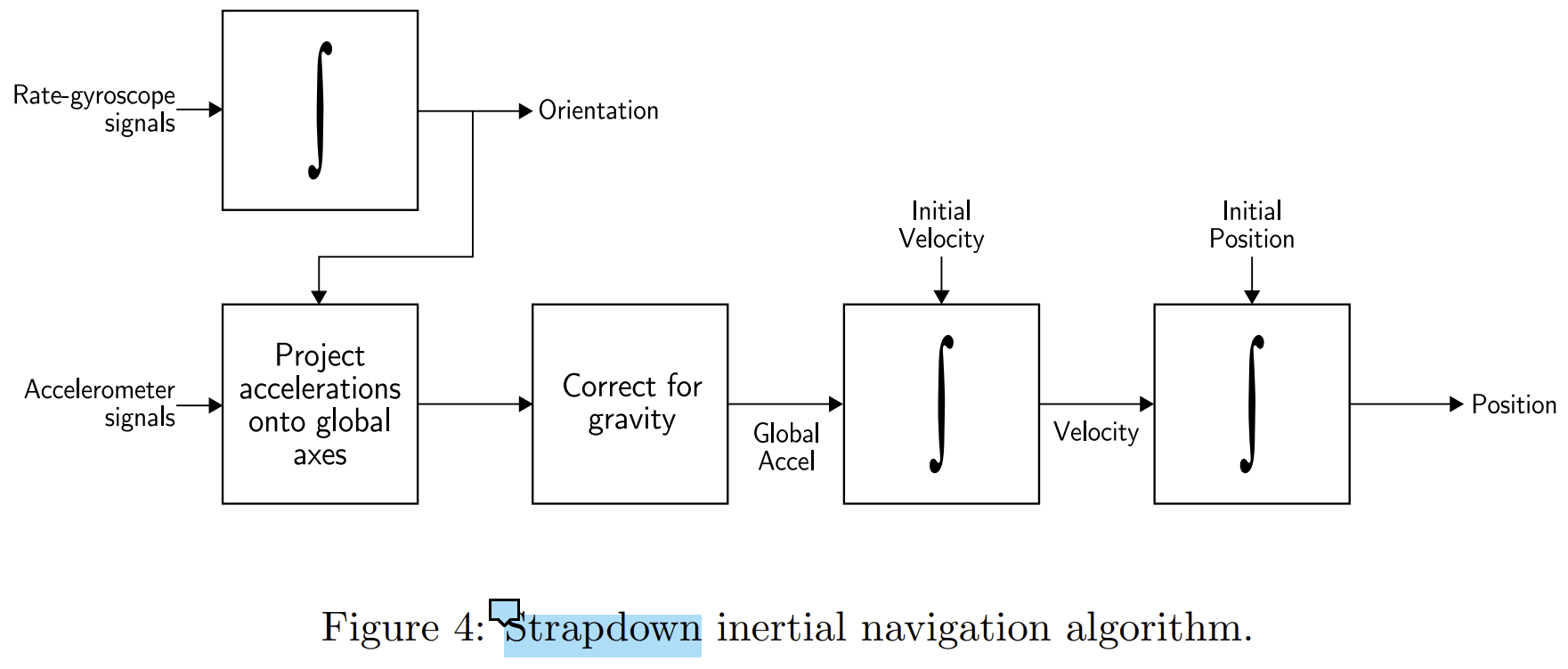可以看到，在捷联系统中，对于位置的计算不仅仅依赖于加速度计的观测，还会用到陀螺仪的观测，而这其实不可避免地引入了更多的误差源。而在平台系统中，由于本体坐标系时时刻刻与全局坐标系对齐，所以计算位置并不需要陀螺仪的参与，计算姿态和位置两者是完全独立的。但不管怎么说，这两种系统计算位姿的基本原理是一样的。

2.陀螺仪基本介绍(Gyroscope)

2.1 陀螺仪的种类

2.1.1 机械式(Mechanical)

一个经典的机械式陀螺仪如下图所示。 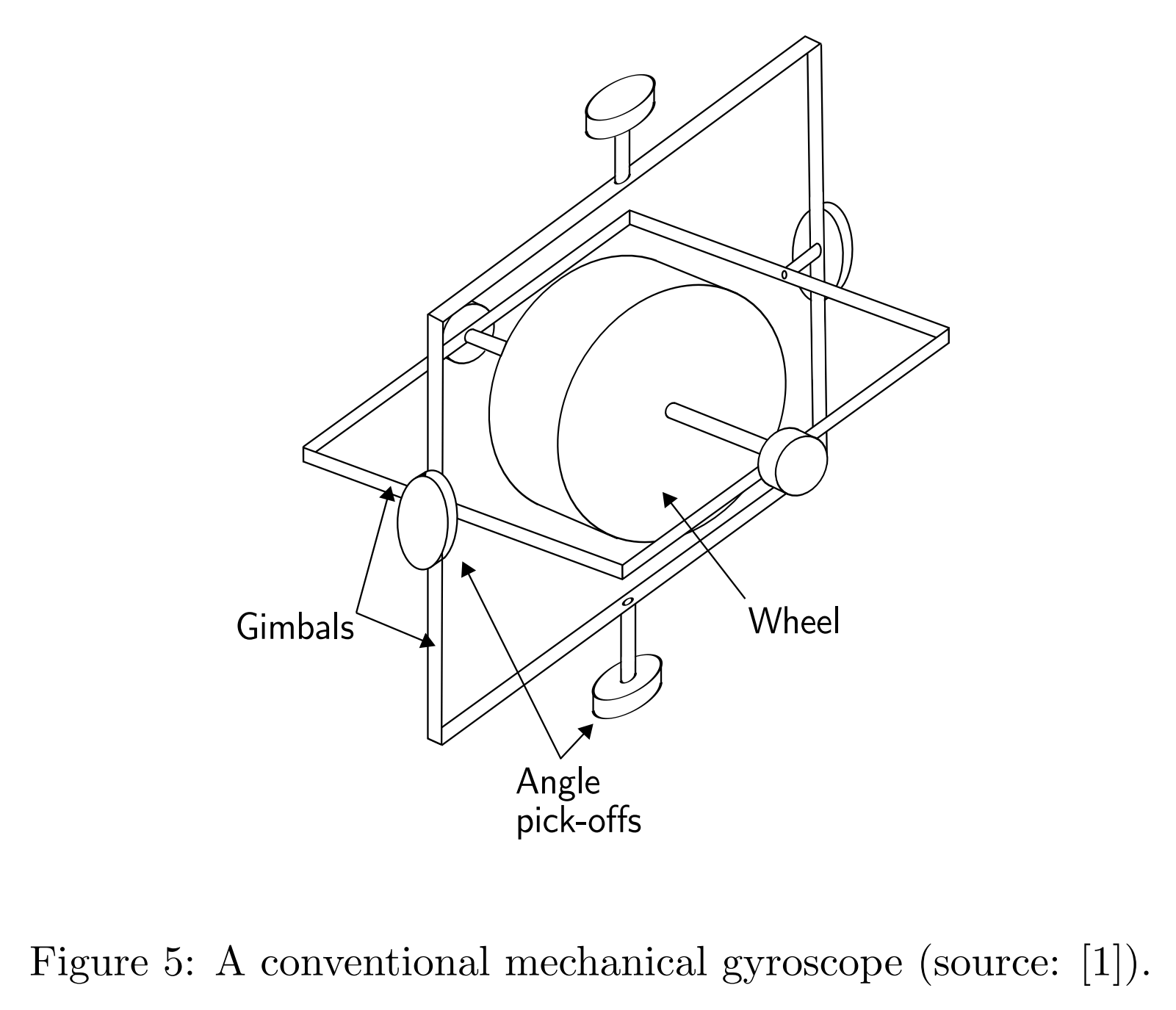由一个旋转轮，两个互相垂直的旋转框(万象架,gimbal)组成。核心原理是角动量守恒(convservation of angular momentum)。当旋转轮高速旋转的时候，如果没有受到外界给它的力，那么它会一直转下去并且旋转轴不变。比如小时候玩的陀螺就是这样：在高速旋转的时候，陀螺会转的很稳，但因为存在和地面的摩擦力，陀螺的旋转逐渐变慢，最后倒下。对于陀螺仪而言，旋转轮一直保持姿态不变(陀螺的定轴性)，当物体运动的时候，万象架就会自然调整来反映这种姿态的变化，如下面的动图所示。 最后，通过读取万象架上的刻度或者两个状态刻度的差异就可以得到运动物体的姿态或者姿态改变量。这便是机械式陀螺仪能用来测量姿态最基本的原理了。感兴趣的话可以参考这个视频，说的也比较清楚。

当然，这里需要注意的是，传统机械式陀螺仪测量的姿态，通过读取万象架上的刻度直接获得。这与目前主流的陀螺仪是不同的。目前主流陀螺仪测量的是角速度，所以又被称为rate-gyros。传统机械陀螺仪的一大问题在于需要包含一个运动部分(也就是转盘)。由于有摩擦力的存在，会导致误差随着时间慢慢增大(漂移)。因此为了解决这个问题，会像设备中加润滑油。当然这不可避免增加了成本。此外，传统机械式陀螺仪还需要几分钟来“热身”，才能使用，这也是比较麻烦的地方。

2.1.2 光纤式(Optical)

光纤式陀螺仪(fibre optic gyroscope, FOG)使用光的干涉(interference)来测量角速度。光纤陀螺仪主要由光纤线圈构成，基于萨格纳克效应(Sagnac Effect)。简单来说就是：将同一光源发出的一束光分解为两束，让它们在同一个环路内沿相反方向循行一周后会合，然后在屏幕上产生干涉，当在环路平面内有旋转角速度时，屏幕上的干涉条纹将会发生移动，这就是萨格纳克效应，如下图所示。 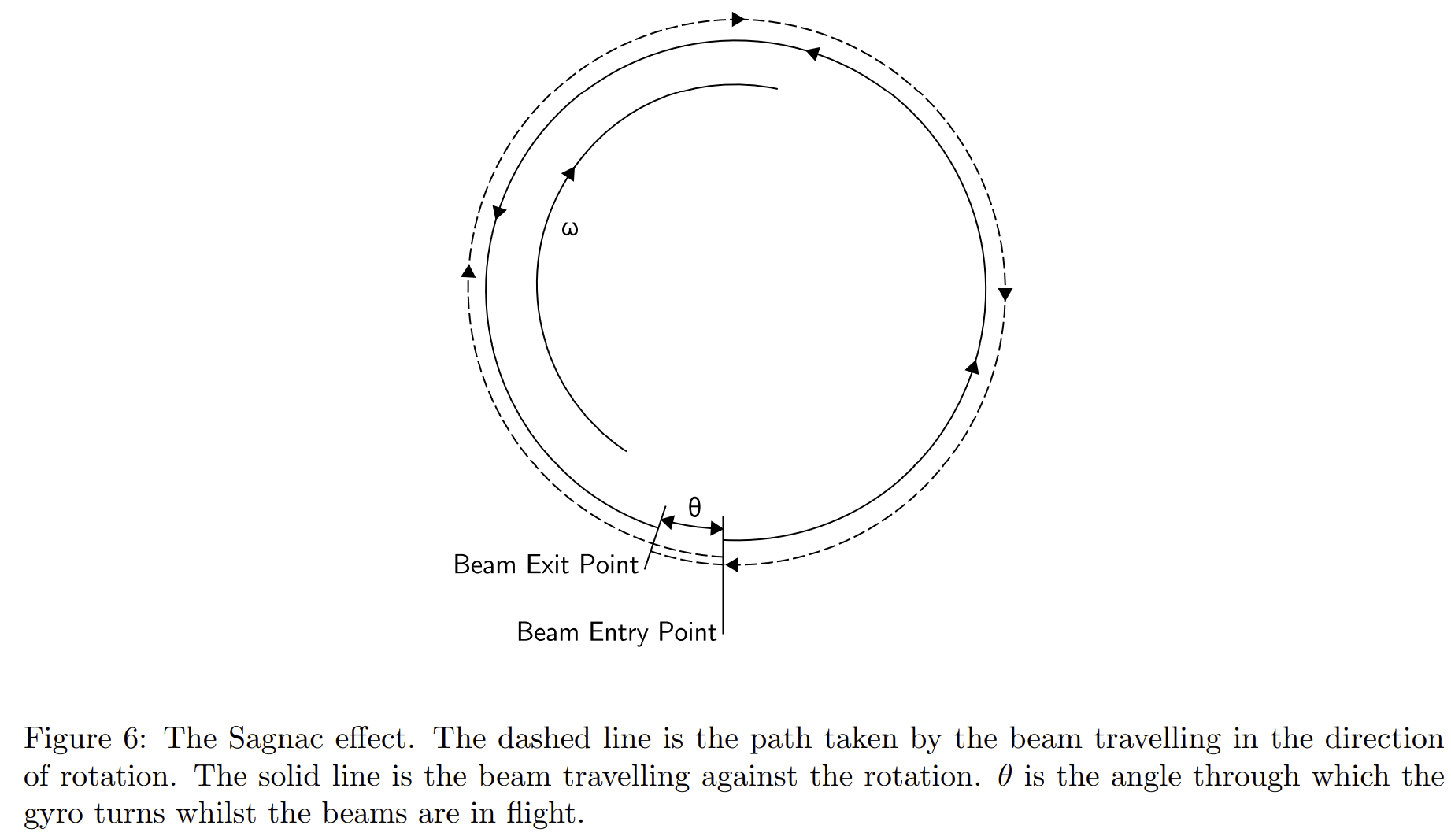通过测量干涉条纹移动的大小，就可以估计出旋转的角速度。

此外，还有环状光纤陀螺仪，也叫做Ring laser gyroscopes(RLGs)。与FOG相比，RLG使用镜子来构造一个闭环光路，光线在这个光路中游走，而不是在光纤中传输。一个实际的光纤陀螺仪长这样。 和上面介绍的机械式陀螺仪相比，光纤陀螺仪不包含运动部分，并且只需要几秒钟的时间来启动。光纤陀螺仪的精度很大程度上取决于光路的长度(越长越好)。当然光路的长度也是受设备的大小所限制的，不可能无限长。

2.1.3 微机电式(MEMS)

上面说的机械式和光纤式陀螺仪都有一个特点：就是精度比较高，但是很贵。作为对比，MEMS式的陀螺仪就便宜很多，当然精度也就稍差一些。MEMS全称Micro-Electro-Mechanical System，中文为微机电系统。感兴趣的话可以搜索更多资料，这里不再赘述。如同前面说的，机械式陀螺仪基于角动量守恒，光纤式陀螺仪基于萨格纳克效应，MEMS陀螺仪则是基于科里奥利效应(Coriolis Effect)。所谓科里奥利效应，对应一种实际并不存在的力——科里奥利力。在一个以角速度\(\omega\)旋转的坐标系中，一个质量为\(m\)的物体以\(v\)速度运动，那么它将会收到一个力，这个力就是科里奥利力，计算公式如下。

这样说可能比较抽象，下面的一段动图很好地解释了科里奥利效应。片段还是来自上面提到的那个视频。 可以看到，球在被人抛出以后，本身就不再受其它外力(重力、空气阻力等除外)。但在旋转的人视角看来，它却走出了一个曲线，而非直线。为了解释这种现象，就虚拟出了科里奥利力。它惯性作用和非惯性系之间的关系。

那么MEMS式如何利用科里奥利力来获得角速度的呢？先介绍基本原理。简单来说，就是测量由于运动而产生的科里奥利力。 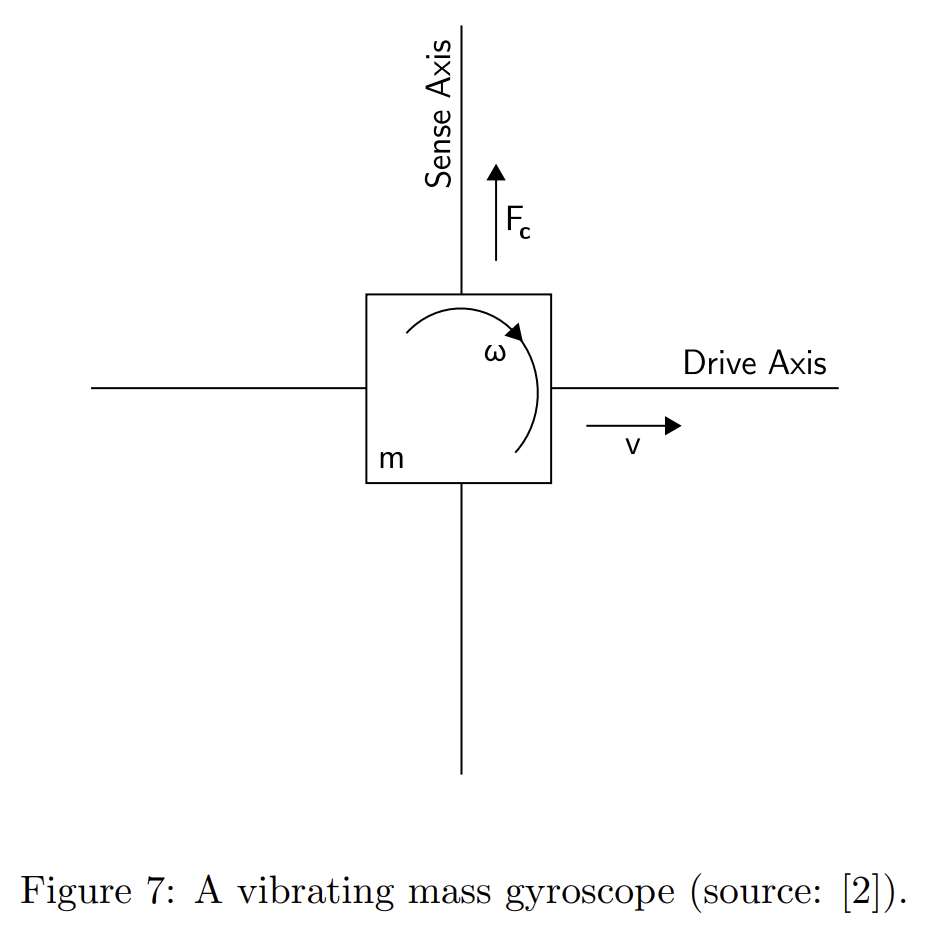可以看到，某个质量为\(m\)的物体水平方向有个速度为\(v\)的运动，同时又存在一个速度为\(\omega\)的角速度。因此，它就会在垂直方向受到一个科里奥利力\(F_{c}\)。测量这个力，再根据上面的公式，可以看到，在已知质量\(m\)、速度\(v\)以及科里奥利力\(F_{c}\)的情况下，就很容易求得角速度\(\omega\)。

然后我们再介绍稍微实际一些的方法。上面说了，只要测量到了科里奥利力就可以求得角速度。那么科里奥利力如何测量呢？答案是可以通过微机械结构电容的变化来间接测量科里奥利力，如下图所示。 首先，我们可以使用压电效应制作出一个在平面中往复振动的机构。当传感器发生特定方向的旋转时，该往复振动就变成了旋转体系中的径向运动，从而受到一个将振动体拉离振动平面的科里奥利力，振动体随之发生形变。传感器通过检测振动体与底面间的微小电容变化，来对旋转速度进行计算测量。

所以一个MEMS陀螺仪测量角速度的流程就是，首先通过压电效应让某个质量为\(m\)的微机械结构以速度\(v\)径向运动。然后又通过电容的变化测量到科里奥利力\(F_{c}\)。这样再利用上面的公式就可以很容易算出在某个轴的角速度\(\omega\)。下面动图进一步展示了这个过程。 而下图展示了iPshone中的三轴陀螺仪。

那么MEMS陀螺仪和前面的机械陀螺仪、光纤陀螺仪相比，有什么特点呢？罗列如下：

• 小尺寸
• 质量轻
• 结构坚固(不易损坏)
• 低功耗
• 启动时间短
• 生产、购买成本低
• 高可靠性
• 在一些挑战场景中也可以较好工作

上面是它的优点。而它最大的缺点就是精度远远低于机械或者光纤陀螺仪。下表对比了光纤陀螺仪和MEMS陀螺仪的一些参数，就可以更好体会上面说的这几点了。

2.2 MEMS陀螺仪的误差特性

本部分主要介绍MEMS陀螺仪中的误差以及它们对积分过程(角速度积分得到姿态)的影响。

2.2.1 常量偏置(Constant Bias)

陀螺仪的偏置是指陀螺仪没有经历任何旋转的情况下，陀螺仪的平均输出。因为理论上，陀螺仪没有经历任何旋转，输出的角速度以及一段时间内的角速度均值都为0。陀螺仪偏置单位为\(^{\circ} / h\)。如果某个陀螺仪的偏置为\(\epsilon\)，那么在积分求解姿态时，它会导致一个随时间线性增长的角度误差\(\theta(t) = \epsilon \cdot t\)。

如何消除陀螺仪的常量偏置呢？也比较简单。我们可以将陀螺仪静止放置在某处，记录其长时间的输出并对其求平均。这个平均值就被作为该陀螺仪的常量偏置。对于偏置的消除也非常简单，就是对于每个陀螺仪的输出，都减去这个偏置量即可。

上面说了这么多，其实你会发现，所谓陀螺仪的偏置可以看作是一种非常低频、几乎不随时间变化的常量系统误差。有时候也会被称为陀螺仪的零偏。这部分知识在之前的这篇博客中也有一些介绍。

2.2.2 热机械白噪声/角度随机游走(Thermo-Mechanical White Noise/Angle Random Walk)

MEMS陀螺仪会受到一些热机械噪声的影响，它的频率远比传感器的采样频率要高。这种机械噪声会给积分的结果引入一种零均值随机游走误差，这种误差的标准差可以用下面的公式表示：

可以看到，角度随机游走噪声的标准差与时间的平方根成比例(换句话说，时间越长，误差越大)。因为我们对于热随机噪声对积分信号的影响更感兴趣，所以，我们通常在设备上标明角度随机游走噪声(Angle Random Walk, ARW)，比如如下。

它的单位是\(^{\circ} / \sqrt{h}\)。比如某个陀螺仪的ARW是\(0.2 / \sqrt{h}\)，就表示一个小时以后，角度误差的标准差为0.2度，两个小时以后为\(\sqrt{2} \cdot 0.2 = 0.28\)度，以此类推。当然还有其它表示方法，如功率谱密度(Power Spectral Density,单位\((^{\circ}/h)^{2}/Hz\))、FFT噪声密度(单位\(^{\circ}/h/Hz\))。它们彼此之间可以相互转换，公式如下：

通过上面的介绍可以明白，角度随机游走噪声可以看作是热机械噪声的表现，反过来，热机械噪声是角度随机游走噪声的成因。只是因为我们更加关注热机械噪声对角度积分结果的影响，而非它本身，所以采用了角度随机游走噪声来表示。

2.2.3 闪变噪声/偏置稳定性(Flicker Noise/Bias Stability)

另一方面，由于电子器件的闪变噪声(Flicker Noise)影响，MEMS陀螺仪的偏置也不会一直不变，而是随时间游走。因此，偏置稳定性就是用于描述某个设备在一段时间内(比如100s)偏置的变化情况。偏置稳定性一般用\(^{\circ}/h\)或者\(^{\circ}/s\)做单位。举个例子，我们知道了在t时刻，陀螺仪的偏置为\(B_{t}\)，偏置稳定性为100秒内\(0.01/h\)。这意思就是说，在t+100秒的时候，此时的偏置为\(B_{t}\)，标准差为\(0.01/h\)。偏置稳定性有时也会通过偏置随机游走计算，如下所示。

这里的\(t\)为偏置稳定性定义的时间长度，比如100s。这里需要说明的是，如果我们认为偏置满足随机游走模型，那么它对于角度积分结果的影响是二阶的。事实上，偏置并非严格满足随机游走模型，只有当时间间隔比较短的时候，才认为近似比较准确。

2.2.4 温度影响(Temperature Effects)

很容易理解，气温的变化也会对陀螺仪造成影响。具体来说，由于气温变化导致的角度误差随时间线性增长。对于MEMS陀螺仪来说，偏置与温度的关系通常是高度非线性的。有些IMU自带了温度传感器，可以用于校正。

2.2.5 校正误差(Calibration Errors)

主要指尺度因子、对齐、陀螺仪线性化等误差。这些误差通常只有在陀螺仪启动的时候才会被观测到，并且会导致累积漂移，它们的幅度与运动的速度和时长成比例。现代一些先进的IMU在内部就会对这些误差进行校正，输出的信号已经就是经过处理的了。

2.2.6 小节

下表总结了MEMS陀螺仪常见的误差。 可以看到，对于MEMS陀螺仪而言，最主要的就是角度随机游走噪声(由于未补偿的温度波动引起)和未校正偏置(由于初始偏置估计误差引起)。这两种噪声一个可以看作是静止的系统误差，不随时间变化，但对角度积分的影响随时间线性增长，一个则是随机误差，随时间变化，对角度积分的影响与时间的平方根成比例。

3.线性加速度计基本介绍(Linear Accelerometer)

3.1 加速度计的种类

总体而言，加速度计可以分为机械或者固态两大类。MEMS其实也可以看作是机械类的一种，只是特别一些，所以单独拿出来。

3.1.1 机械式

一个传统的机械式加速度计由固定着一个质量块的弹簧组成，如下图所示。 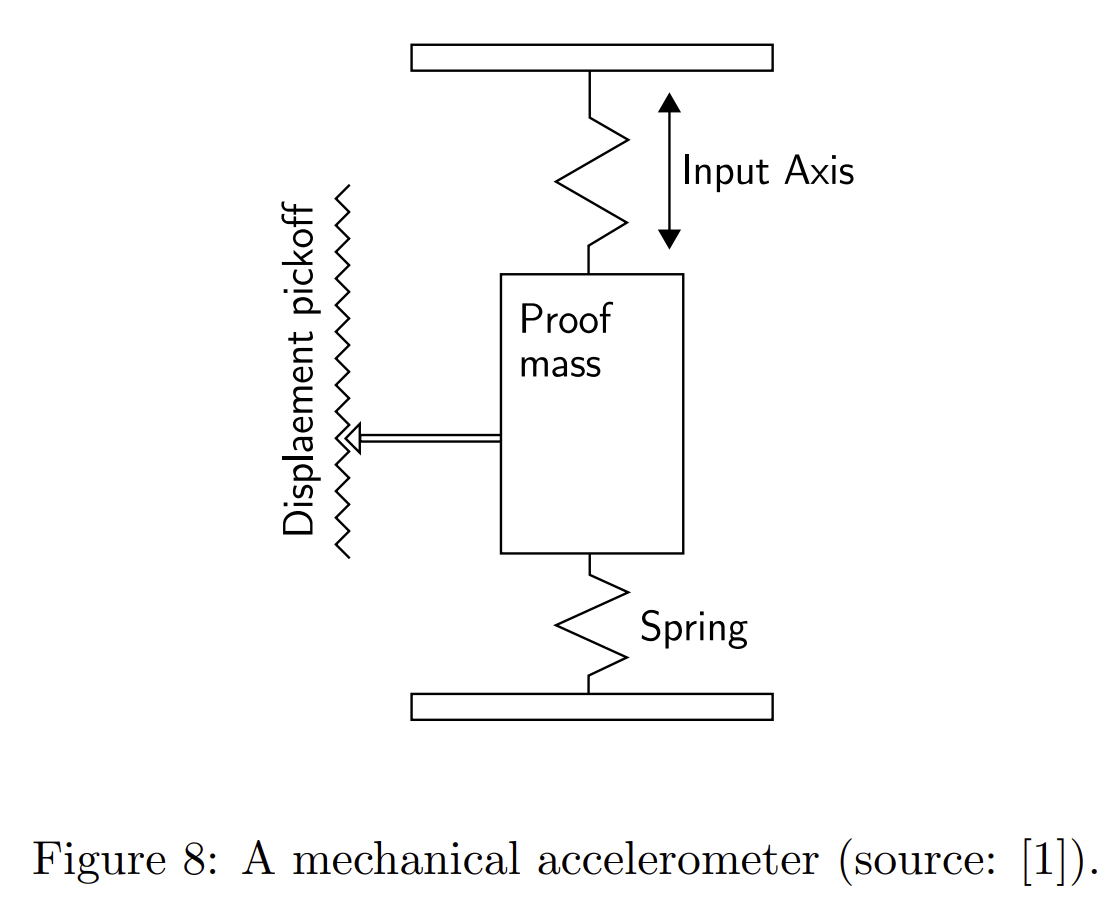在装置中，我们可以通过刻度来获得质量块的位移，这个位移量是与施加在它上面的力F成比例的，所以我们可以根据位移反推施加的力F。再根据牛顿第二定律F=ma，此时F、m都已知，就可以求得测量方向上的加速度a了。原理非常简单。

3.1.2 固态

固态加速度计可以进一步分为表面声波类(Surface Acoustic Wave)、振动类(Vibratory)和石英类(Silicon and Quartz)。比较常见的是表面声波加速度计，如下图所示。 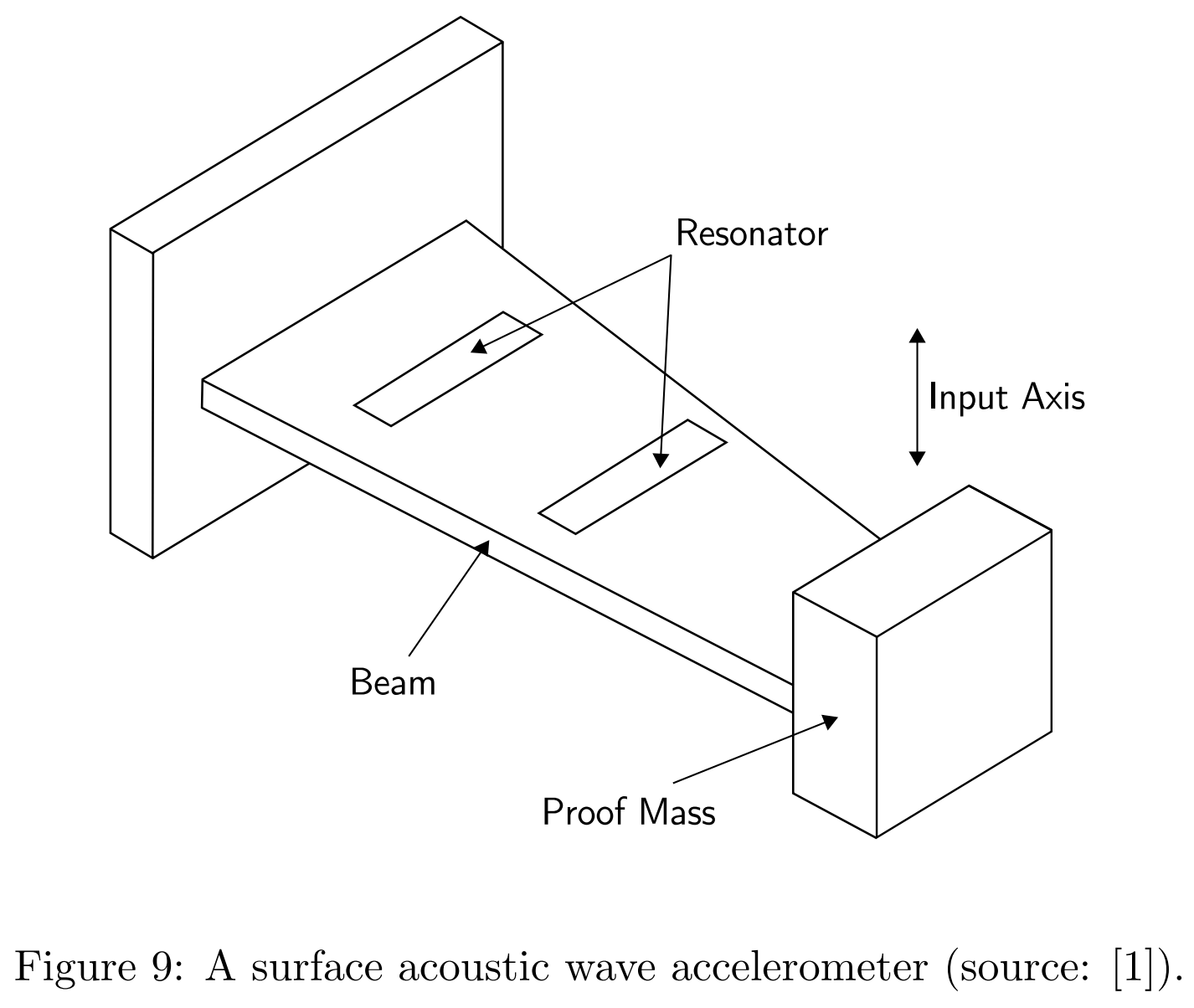其包含一个以特定频率振动的悬臂，一端固定在平台上，另一端固定了一个小质量块。当测量方向上有加速度的时候，悬臂就会弯曲。这就会导致悬臂的振动频率发生改变，并且这种改变是与施加在上面的力成比例的。通过测量频率的变化，我们就能间接测量得到力，再根据牛二定律，就可以计算出加速度。

3.1.3 MEMS

主要有两类MEMS传感器：第一类通过测量质量块的位移来推算加速度，原理与机械式加速度计相同；第二类通过测量振动单元频率的改变来推算加速度，原理与固态加速度计相同。MEMS加速度计的优缺点其实和前面说的MEMS陀螺仪的加速度计是一样的：尺寸小、质量轻、低功耗、启动快，劣势就是和传统加速度计相比不太精确。

3.2 MEMS加速度计的误差特性

如果看内容的话，会发现本部分和2.2部分是非常类似的，事实也是如此。与陀螺仪不同的地方在于，对加速度计而言，误差都会被积分两次(加速度→速度→位移)，而陀螺仪只需要积分一次(角速度→姿态)。

3.2.1 常量偏置(Constant Bias)

加速度计的常量偏置是指它的输出值和真值之间的差异，单位是\(m/s^{2}\)。如果存在某个常量偏置\(\epsilon\)，那么在积分追踪位置的时候，就会被积分两次，对位置解算的影响随积分时间成二次方增长，如下。

如何估计这种常量偏置呢？方法与陀螺仪也是类似的——将加速度计静置，通过测量加速度计长时间段内的输出并取平均，以此作为加速度计的常量偏置。当然了，这里有个潜在问题，就是重力。由于受到重力影响，上面的方法不可避免地会将重力计算到偏置之中。所以为了消除重力影响一般需要精确知道重力矢量，这一般可以通过一些特殊设备获得。

3.2.2 热机械白噪声/速度随机游走(Thermo-Mechanical White Noise/Velocity Random Walk)

热机械噪声同样会造成速度上的随机游走，一般单位为\(m/s/\sqrt{h}\)。通过推导，我们可以得到下面的公式：

这里因为假设\(\delta t\)很小，所以可以近似认为加速度计白噪声给位置积分引入了一个二阶的随机游走，它的标准差与时间的3/2次方成正比。

3.2.3 闪变噪声/偏置稳定性(Flicker Noise/Bias Stability)

MEMS加速度计同样受到闪变噪声影响，从而导致偏置随时间游走。所以闪变噪声就给速度引入了一个二阶随机游走，其不确定性与时间的3/2次方成正比，以及给位置引入了一个三阶随机游走，其比确定性与时间的5/2次方成正比。

3.2.4 温度影响(Temperature Effects)

温度与偏置的关系每个设备都不同，但同样是高度非线性的。任何没有被消除掉的偏置都会导致位置上随时间二次方增加的误差。

3.2.5 校正误差(Calibration Errors)

这些误差通常只有在加速度计启动的时候才会被观测到，它们的幅度与运动的速度和时长成比例。现代一些先进的IMU在内部就会对这些误差进行校正，输出的信号已经就是经过处理的了。

3.2.6 小节

MEMS加速度计误差总结如下表所示。 可以看到，对于MEMS加速度计而言，速度游走噪声和未校正的偏置是两个重要的误差来源。

4.捷联惯性导航

在上面我们介绍了很多陀螺仪和加速度计的基本概念和硬件知识，下面我们就进一步介绍以下，到底是如何利用IMU进行惯性导航的。如下图所示，为捷联惯性导航的算法框架。 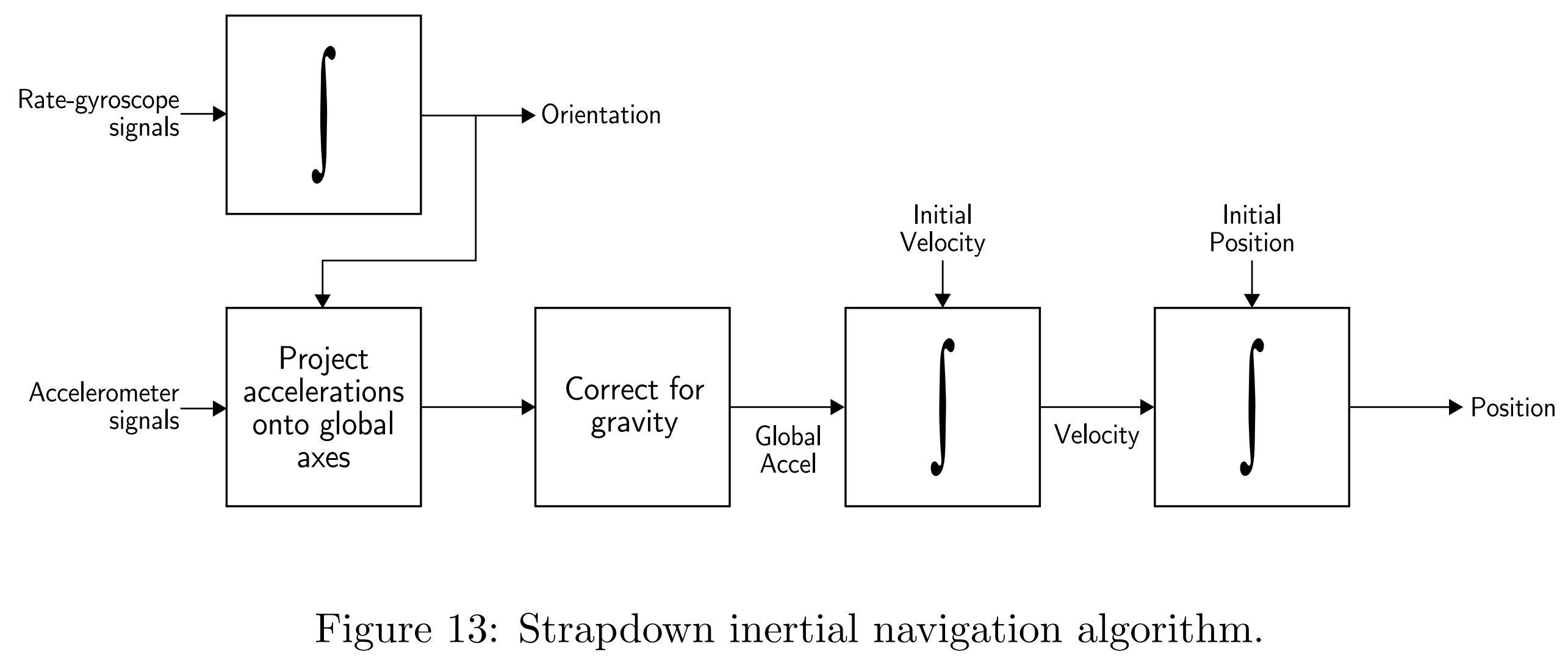下面就会就姿态和位置推算分别进行介绍。

4.1 推算姿态

4.1.1 理论

一句话概述就是：一个惯性系统相对于全局参考系的朝向/姿态可以通过来自系统速率陀螺仪测量的角速度信号(\(\omega _b(t) = (\omega_{bx}(t),\omega_{by}(t),\omega_{bz}(t))^{t}\))积分获得。当然了，表示姿态有多种方式，如欧拉角、四元数、方向余弦等，感兴趣可以参考这篇博客，这里不再赘述。这里我们使用方向余弦来表示姿态。

在方向余弦表示法中，本体坐标系相对于全局坐标系的姿态通过一个3×3的旋转矩阵C指定。这个矩阵C中，每一列都是一个单位向量，表示本体坐标系的坐标轴与全局坐标系坐标轴的关系。所以我们可以得到下面的转换公式：

也就是说，一个本体坐标系下的向量\(v_{b}\)左乘旋转矩阵就可以变换到全局坐标系下。这个转换的逆变换(其实就是对上式左右两边分别乘以旋转矩阵C的逆)如下：

对于旋转矩阵而言，矩阵的逆就等于矩阵的转置。

所以可以看到，我们如果要利用陀螺仪的测量推算位姿，其实就是在求某一时刻的旋转矩阵C。只要有了C，就可以按照上式实现两个坐标系之间的相互转换了。如果某个时刻\(t\)的旋转矩阵用\(C(t)\)表示，那么它在\(\delta t\)时间内的变化可以表示为如下：

这里\(C\)是关于时间\(t\)的矩阵函数，所以以矩阵函数导数表示(上面加一点)。进一步，根据旋转的物理意义，对于\(t+\delta t\)时刻的姿态，它除了直接表示当前时刻本体坐标系与全局坐标系之间的变换关系，我们也可以从另一个角度理解：它是在\(t\)时刻姿态\(C(t)\)的基础上，通过一个旋转得到的。如果我们把这个旋转对应的旋转矩阵记为\(A(t)\)，那么可以有下式：

这里\(A(t)\)表示的就是本体坐标系在\(t\)时刻和\(t+\delta t\)时刻之间的旋转。到这里我们可以发现，这个旋转表达的物理意义其实和陀螺仪的观测量之间已经很接近了。陀螺仪观测的是角速度，如果乘以\(\delta t\)就表示这段时间内的旋转，也就是这里的\(A(t)\)。当然，这种关系还是不够明显，需要继续研究\(A(t)\)。如果我们以\(\delta \phi\)、\(\delta \theta\)、\(\delta psi\)来表示\(t\)到\(t+\delta t\)时刻之间绕着本体坐标系x、y、z轴的微小旋转，按照小角近似，\(A(t)\)可以写成下面的样子：

其中，\(\Psi\)为：

所以，将它代回\(\dot{C}(t)\)式子中，得：

注意这里的\(\Psi\)除以\(\delta t\)的物理意义，它其实就是表示了\(t\)时刻旋转的速度。如果我们以\(\Omega(t)\)来表示上式中的极限部分，如下：

再结合上面\(\delta \Psi\)的展开式子，把矩阵中的每一项都除以\(\delta t\)，即可可到\(\Omega(t)\)，有：

毫无疑问的，一段时间内变化的角度除以时长，得到的就是变化的角速度。可以看到，矩阵中的每个元素都是各个方向的角速度。而这，恰恰就是陀螺仪所观测的量。当然，如果你对反对称矩阵的构成比较熟悉，上面的\(\Omega(t)\)其实就是\(w_{b}(t)\)对应的反对称矩阵。进一步，我们整理一下上面的式子，可以得到如下公式：

对于上式，在t时刻，我们已知的只有\(\Omega(t)\)，要求的就是\(C(t)\)。可以看到这是一个微分方程。我们可以对上式进行变换，得到下式：

可以看到，对于t时刻的姿态，我们只需要知道起始时刻的姿态，以及当前t时刻的角速度，并对其从0到t做积分，并与初始姿态相乘即可得到当前t时刻的姿态\(C(t)\)。这个结果正是我们想要的，我们推了这么半天的目的就是找到陀螺仪的观测量和姿态之间的直接关系。这样之后当我们拿到陀螺仪的观测数据，就可以直接利用公式计算姿态了，十分方便。

4.1.2 实现

在实际中，陀螺仪无法提供连续的观测，而是遵循某一频率的离散观测。因此，我们需要对这些离散的信号进行积分。积分的方法多种多样，但一般而言，如果时间间隔较短，而且对精度要求不高，一些低阶的积分方法，如矩形法则就足够了；而对于一些要求更高的场合，则需要用更高阶(三阶或四阶)的方法。这里我们以矩形积分方法来讨论如何实现。

继续往下介绍之前，简单回顾一下积分的求法。积分起始可以理解为求面积。不论是之前的梯形法还是这里的矩形法，核心就是求面积。对于一个a到b的区间，将其划分为N份，每一份的宽度就是(b-a)/N。而每一份的高度我们可以利用函数获得，比如我们选择每一份最左边的位置作为自变量，它的坐标为i×(b-a)/N，其中i为迭代变量。将其带入函数f(x)，即可得到对应的高度。这样矩形的宽和高都有了，两者相乘，就是这一小块的面积，不断迭代，就可以得到整个面积。当然，这里对于每一小块高度的不同定义，就导致了不同的方法和结果。比如上面介绍的矩形法，如果对于单调增函数而言，它求的积分是偏小的。所以又有所谓的中点矩形法。也就是说，我不把每个小份最左边的数输入函数计算高，而是取这一小份中点的x坐标，带入函数计算。当然还有别的定义方式，把这一小份按照梯形来计算，这一小份的左右两边分别是梯形的上底和下底。前面也说了，这些都是比较低阶(一阶)的积分方法，当然也有更高阶的办法。一个简单的想法就是，在每一个小份中采样多个点，然后用高阶函数拟合曲线，并计算面积。不过如何数值计算积分不在本篇博客的讨论范围，这里也不再赘述。

回到我们刚刚的问题。我们先假设陀螺仪的相邻两次观测的时间间隔为\(\delta t\)，所以对于\([t, t+\delta t]\)时段，根据上面得到的积分公式，可以有下式：

使用上面提到的矩形积分法则，对积分部分进行简化，将其记为\(B\)，如下：

那么\(B\)应该为：

这里\(w_{b}= (w_{bx},w_{by},w_{bz})^{T}\)。因为我们认为\(\delta t\)间隔非常小，在这样的范围内，测量的角速度可以直接和时间相乘，从而得到姿态变化。前面也说了，当然这一步可以采用更加复杂的算法。这样，我们整理将\(B\)代入上面的积分公式有：

到这里，注意一下，我们的目的是什么：我们要根据陀螺仪的观测和上一时刻姿态计算当前帧的姿态。那么我们已知的是什么：就是上时刻的姿态和当前的陀螺仪观测。所以利用上式就可以根据陀螺仪观测直接推算姿态了。这样做可以吗？答案是可以的，没毛病。但有一点点“瑕疵”。那就是公式中还有个\(exp()\)，而且还是对一个3×3的矩阵做，这或多或少有点复杂。所以我们能不能把上式再可接受精度的范围内简化一下，把\(exp()\)去掉呢？答案同样是肯定的。这时候就要请出大名鼎鼎的“泰勒展开”了。可以看到，在上式中，存在一个指数函数\(e^{B}\)。指数函数的泰勒展开公式如下：

这里我们令：

它是一个标量。然后我们根据指数函数的泰勒展开公式，对上式进行简化，如下：

可以看到，在将指数函数泰勒展开以后，人为地构造了sin和cos的泰勒展开，并最终得到了相对简单(没有指数函数)的式子。在这个式子中，我们拿到陀螺仪观测和时间间隔以后，就可以直接计算了。

4.1.3 误差

MEMS陀螺仪主要包含白噪声和偏置噪声。白噪声会导致角度随机游走，其标准差随时间的平方根增长。偏置噪声会导致姿态的误差，其随时间线性增长。

4.2 推算位置

4.2.1 理论

我们的目标就是根据t时刻加速度计的观测\(a_{b}(t)=(a_{bx}(t),a_{by}(t),a_{bz}(t))^{T}\)来推算此刻的在全局坐标系下的位置。首先我们需要将本体坐标系下的加速度转换到全局坐标系下，可以用下式表示。

然后，我们将重力从加速度中减去。并对剩余的加速度进行两次积分：一次积分变成全局坐标系下的速度，二次积分变成全局坐标系下的位置，如下式表示。

这里\(v_{g}(0)\)为设备的初始速度，\(s_{g}(0)\)为设备的初始位置，\(g_{g}\)是全局坐标系下的重力加速度矢量。如果我们把这几个式子合在一起，可能会看得更清楚一些，如下：

可以看到，在t时刻，我们只要知道了此时的姿态\(C(t)\)(由陀螺仪测量、计算)以及加速度计测量的加速度\(a_{b}(t)\)就可以一步步求得全局坐标系下的位置：先将加速度转化到全局坐标系，再减去重力，对剩余部分积分得到速度，再将初始速度加到积分的速度上得到总速度。最后对速度再做一次积分，得到位移，再加上初始位置，即为最终在全局坐标系下的位置。

这样，位置积分就完成了。可以看到，相比于姿态，位置积分要简单很多。同时也可以看出，位置计算是依赖于陀螺仪的积分结果的。因为设计到某时刻本体坐标系和全局坐标系之间的转换关系，这个转换关系只有通过陀螺仪才能得到。这样做的结果是，如果陀螺仪有了比较大的误差，那么位置的估计也不会好。

4.2.2 实现

相比于姿态，位置积分公式简单许多。只有一个积分过程需要“简化”一下。这里我们同样采用矩形法则进行数值积分，如下：

可以看到，只需要知道加速度计的观测以及此时在全局坐标系下的姿态，即可以推导位置。

4.2.3 误差

在两次积分的过程中，加速度计本身存在多种可能的误差源，显然，这样会导致位置计算的漂移。另一方面，由于位置积分算法依赖于陀螺仪，陀螺仪本身的误差同样也会影响位置计算。从陀螺仪观测中计算的旋转矩阵\(C\)被用于将本体坐标系下的加速度转换到全局坐标系下。如果这个旋转矩阵不准就会导致：一加速度在错误的方向上进行积分；二重力分量难以被干净地去除。

5.参考资料

• [1] https://haokan.baidu.com/v?pd=wisenatural&vid=4917207119914294731
• [2] http://www.leadgentech.ai/nd.jsp?id=12