本篇博客是旷视CV Master训练营系列《基于神经网络的3D重建》专题的第二课《基于NeRF和SDF的三维重建与实践》的相关笔记，课程视频可以点此查看。
0.本次内容
在之前的课程，我们介绍了NeRF和Plenoxel的基本内容。这些方法固然有很多优点，但缺点也是比较明显的。比如上篇笔记中说过的，NeRF是对场景的“隐式表达”，所以对于每一个场景都要单独进行训练，得到该场景的表达。这个过程是比较耗时耗力的。Plenoxel相比于NeRF有更高效的性能表现，同时又保证了重建的质量。但它的问题在于计算的开销和存储都非常大。因此，这节课的主要内容之一就是探讨如何加速模型。本节课另外一个重点是如何基于一个训练好的NeRF得到场景的三维表示(比如三维格网)。
1.基础知识
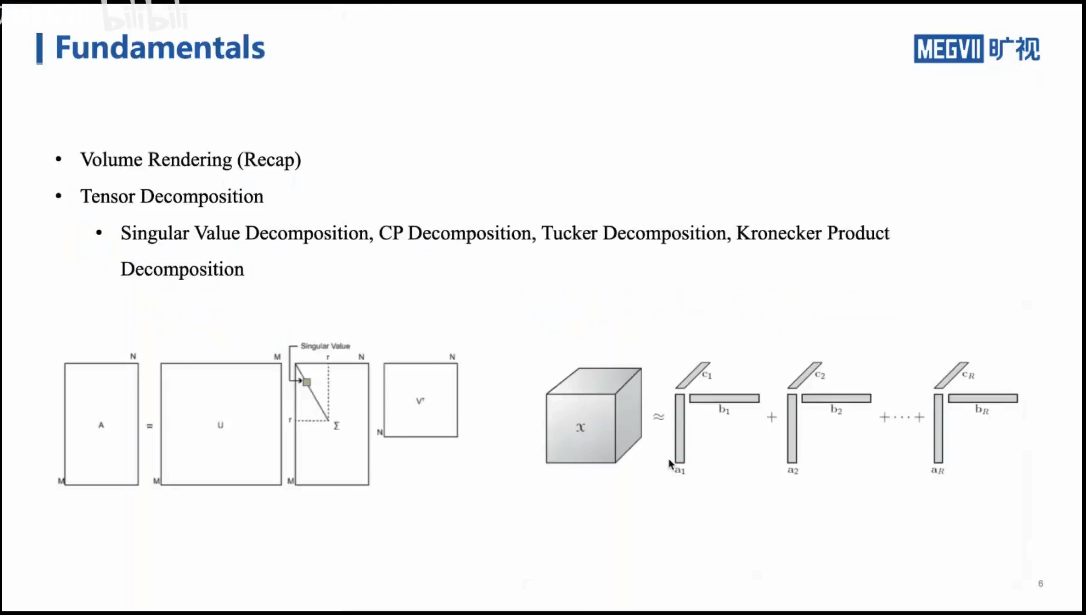这一部分主要包含体渲染(Volume Rendering)和张量分解(Tensor Decomposition)两部分。
1.1 体渲染
如上图所示，NeRF的计算量还是挺大、比较耗时。对于一个乐高积木的场景，单卡2080Ti可能需要七八个小时的训练时间，这样很难落地到实际应用中。尽管如此，NeRF的框架还是有参考价值的。我们的NeRF输入是一个位置坐标(x,y,z)以及一个方向(θ,φ)(上节课也说了，以类似经纬度的方式表示射线方向)，输出就是在该位姿下，观察该场景对应的颜色场和密度场。最后，我们再通过体渲染的方式，就可以得到渲染出的图像了。我们可以对渲染出来的图片和真实图片做Loss，这样不断迭代，就可以优化MLP，使得网络能够记住当前的场景。可以看出，在上述的过程中，一个很重要的环节就是体渲染。更具体来说就是根据三维场景渲染出二维影像(把三维数据映射到二维平面上)，也就如上图中的公式所示。理想的公式是沿着光线，颜色和密度都是相对平滑的函数，我们直接对它们沿着光线积分，得到的结果就是这一束光线在像平面上的颜色。在实际中，积分并不方便计算，所以我们进一步对理想积分公式进行离散化，得到最终可计算的公式。
1.2 Plenoxels
NeRF本身是纯隐式表示，完全由MLP来记录场景。事实上，除了用MLP来表示三维场景，我们还可以显式地表示三维场景，如利用体素(Voxel)构建地图。比如我们上节课介绍过的Plenoxel就是一个基于体素的、完全的显式表示方法。可以看到，相比于NeRF，他的优势在于快速、高质量，但是一个“很重”的方法。因为引入体素以后，有较大的计算开销。如果把训练好的模型存下来，可能有几百兆或者一个多GB的大小(与选择体素的密度有关)。如果我们把三维的体素看成是张量，那么就可以用一些张量压缩的方法在一定程度上进行压缩。可以看到，NeRF是基于MLP的纯隐式表达，而Plenoxel是基于体素的纯显式表达。那么有没有可能把两者结合起来呢？答案是肯定的。在后面的部分会进一步介绍。
1.3 张量分解
什么是张量？可以简单理解为是多维的数据，0阶的张量就是标量，1阶的张量是向量，二阶的张量是矩阵。以二维矩阵分解为例，可以采用SVD进行分解。我们把二维的分解扩展到三维，就可以得到三维张量分解的方法。
1.3.1 CP分解
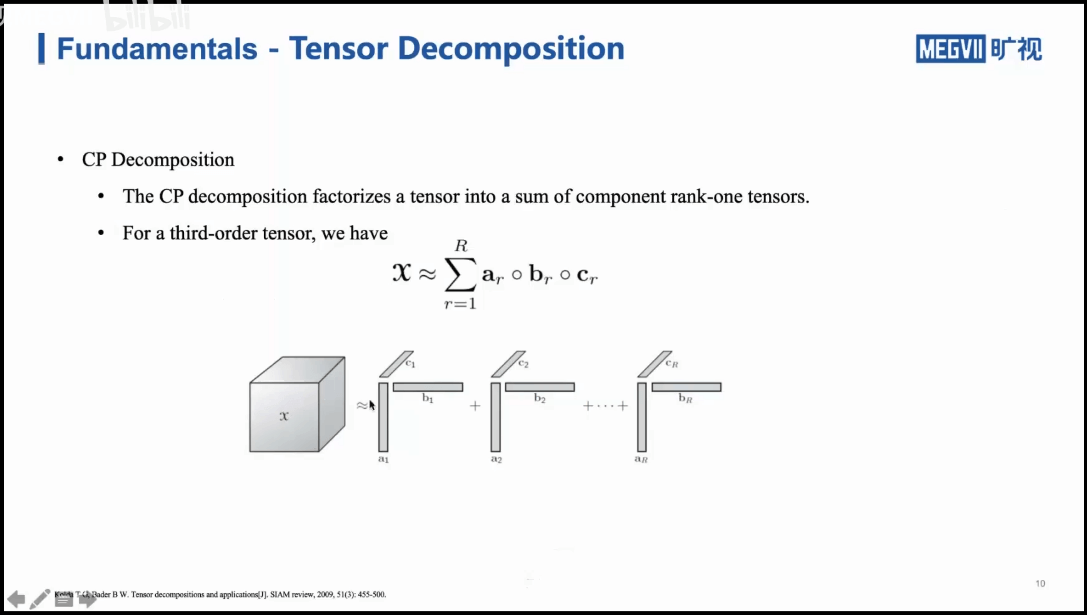如上图所示，比如我们有一个三维的矩阵，我们也可以将其分解为多个秩为1的张量的和，每个向量可以由三个向量来表示。这里其实就有点类似于三维向量的分解。对于某个向量，我们分别将其投影到x、y、z轴上，得到在三个方向上的分量。反过来，我们根据这三个分量，也可以恢复出一个三维向量。在张量分解里，这些由三个向量组成的张量就可以看做是一种“分解基”。这样做的好处是什么呢？本来可能我们要存储一个很大的三维矩阵，每个点都需要存，但是分解以后，就可以只存一些向量就能够表示这个三维矩阵，可以节省存储空间。
1.3.2 Tucker分解
如上图所示，是另一种三维张量的分解方式。可以将一个大张量分解为一个核心张量以及A、B、C三个小的矩阵。通过运算就可以恢复出原始的张量。
2.Fast Radiance Fields
2.1 KiloNeRF
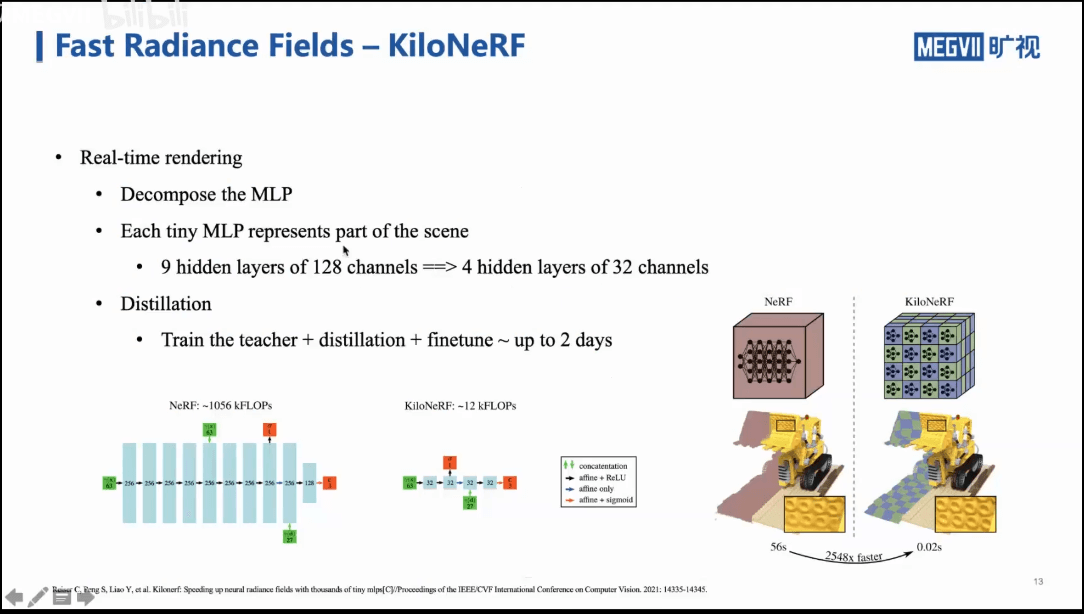如上图所示，一个非常简单的分解想法就是，我们可以用一整个MLP表示三维场景，那么也可以将这个三维场景进行切割，分成很多小块，每一个小块都用一个小的MLP进行学习。此外，也基于知识蒸馏的策略进行训练。可以发现，整个训练的过程耗时还是比较长的，但是推理时间很短，如下图所示。
事实上，这个工作除了在原理上相比于NeRF进行了改进，也加入了一些工程上的改进策略，比如CUDA实现等。
2.2 Instant NGP
前面说了NeRF是隐式，Plenoxel是显式。事实上，Instant NGP就是将显式和隐式结合起来的工作，如下所示。左边可以看作是体素，右边是MLP。
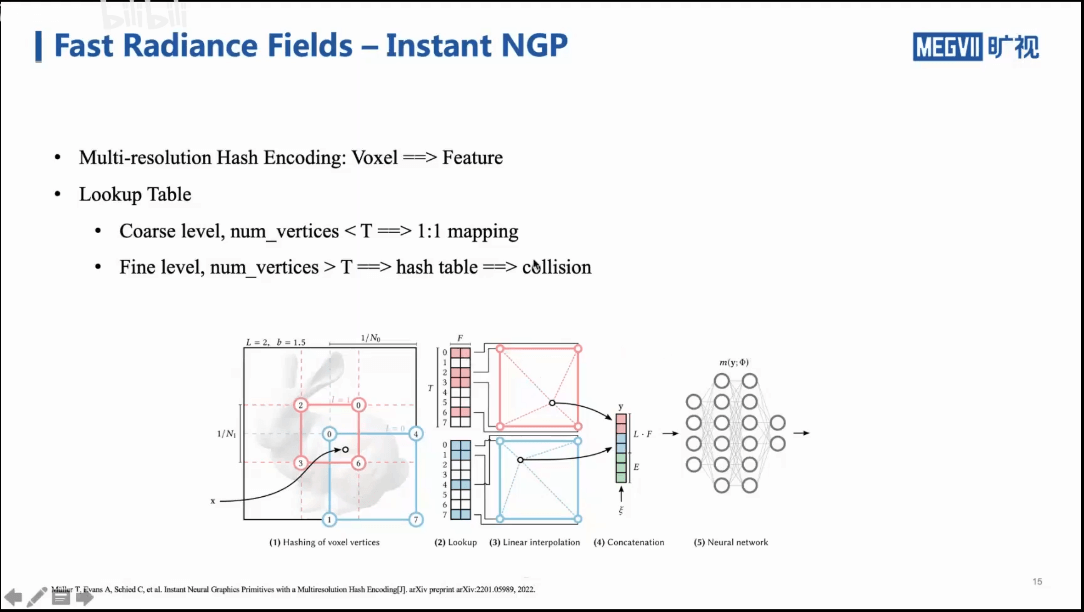在显式的部分，我们通过哈希编码实现对位置的编码。这一部分可以类比NeRF的positional encoding。简单来说，对于上图中的左边部分，我们将其看作是一个体素。我们可以对这个体素进行多尺度的分割，比如分成2×2的蓝色网格、3×3的红色网络。我们通过哈希编码将位置和特征进行绑定。最终，我们根据具体位置进行插值，最终得到一个一维特征向量。这个一维特征向量是由不同尺度的特征组成的。比如图中的红色部分就是由3×3的网格得到的。最后，绿色部分表达方向信息。具体而言，是通过球面谐波系数编码的，和Plenoxel相同。通过这样的方式，我们就可以将一个很大的体素映射到特征，给MLP输入这些特征再去学习。当然，这个方法也有一些缺点。比如，如果体素的顶点数量超过了特征的长度，也就可能出现多个顶点对应一个特征位置的情况。这样就会造成冲突。这个问题在论文中进行了解释，如下：
第一点就是，尽管存在冲突，但作者认为这种冲突影响不大。第二点，后面接的MLP在一定程度上可以解决这个问题。
2.3 TensoRF
前面我们分别说了两种加速方法，一种是分解MLP，另一种是通过哈希编码。这一种方法则是前面说的基于张量分解的方法，如下所示。
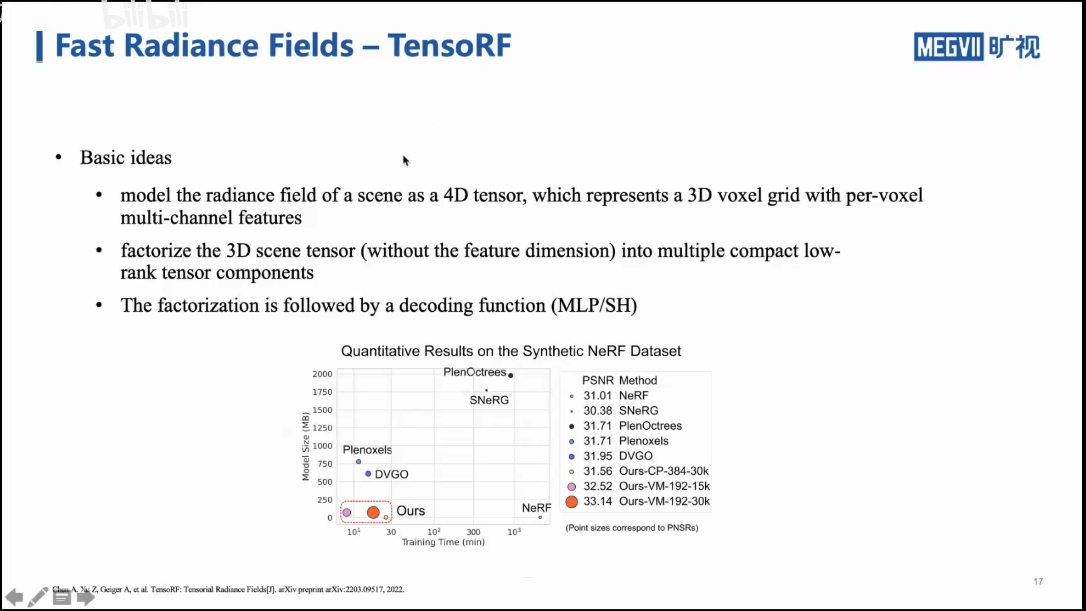他的主要框架也是Plenoxel+MLP。通过张量分解实现加速。
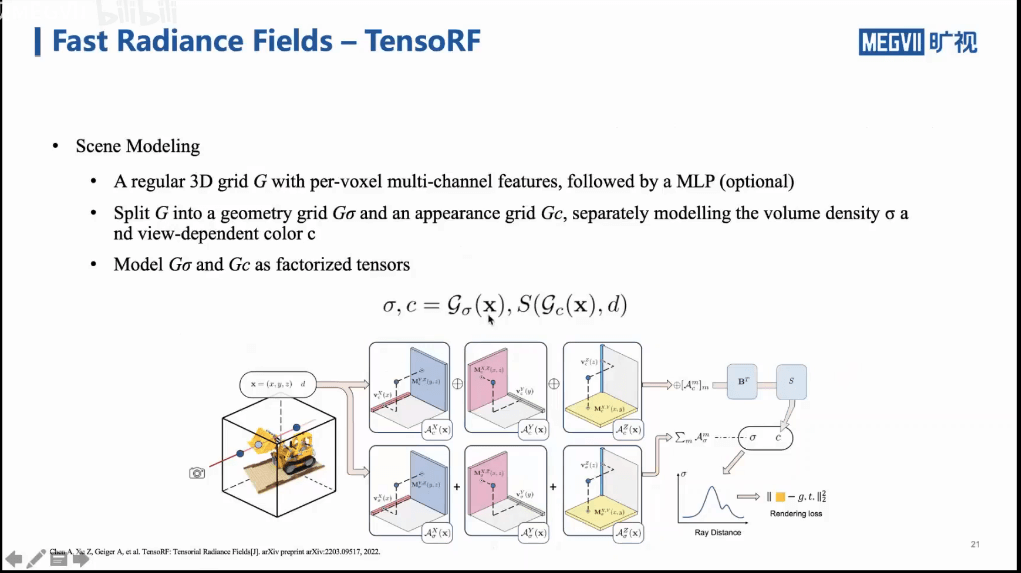
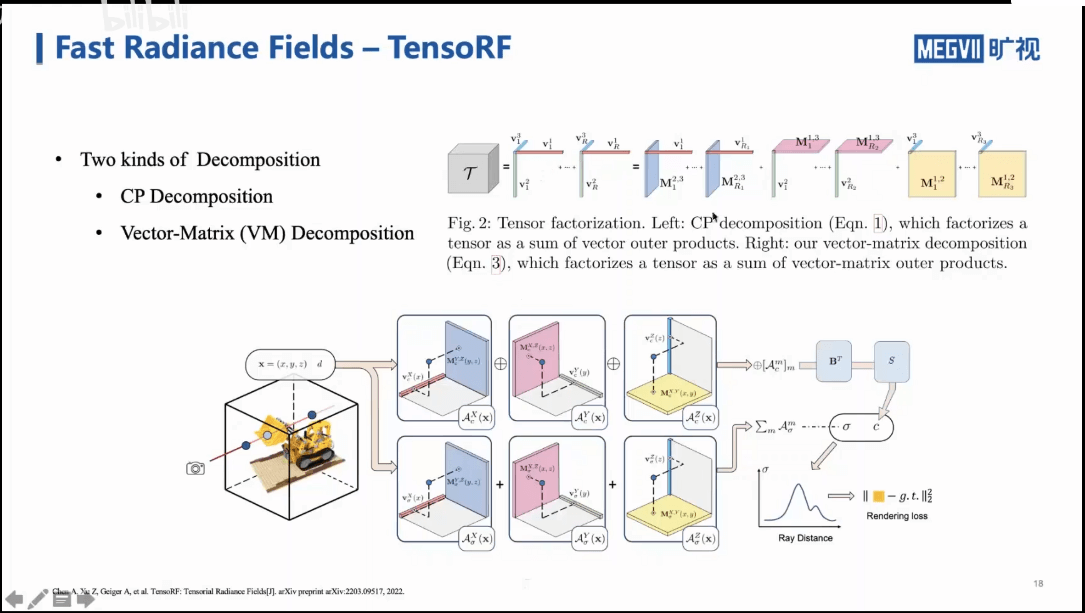如上图中上部分所示，对于一个张量，我们可以进行CP分解，也可以进行Vector-Matrix分解(论文中提出的方法)。简单理解就是将张量分解为一个矩阵+一个向量的形式。整个框架和NeRF保持了一致，如上图下部分所示。输入就是一个空间点，输出就是颜色+密度。然后按照渲染积分公式得到一张图，最后对预测的图与真值做Loss，进而优化更新网络。同时也可以看到，这里作者对于颜色场和密度场分别进行了分解。比如密度可能相对变化不那么大，那么就可以选择稍微低阶一些的近似，可以减少复杂度。
3.Multi-view Reconstruction with SDF
在上一次课和这次课中，我们说了很多NeRF。但核心的pipeline都是一样的。得到网络以后，可以合成出不同位置的影像，将这些影像组合起来就能得到一个看起来比较“炫酷”的视频。但是，我们能不能把NeRF所包含的三维信息给导出成三维模型呢？答案是可以的。
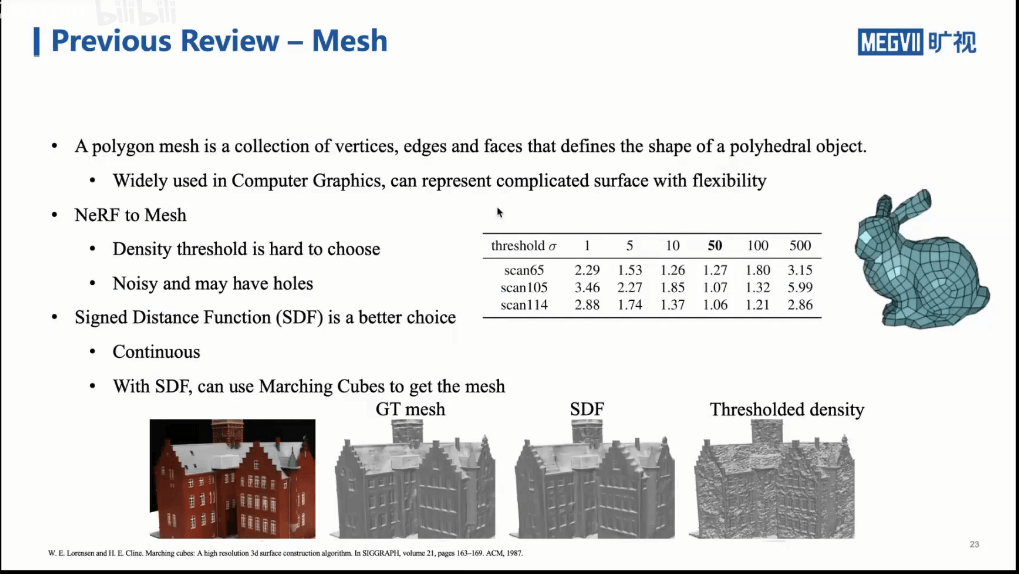一个简单的方法就是，基于NeRF生成的体密度做阈值化。这样就可以把所有有密度的区域留下来。但这样的问题是得到的三维模型可能是不够精确、噪声也是比较大的。而且更大的问题是，这个阈值该如何设置？所以一个更好的办法是采用有向距离场Signed Distance Function(SDF)。在进一步介绍之前，下图给出了基于体积渲染的多视三维重建的输入和输出。
我们的输入就是一堆带有位姿的2D影像，输出则是利用SDF得到的三维Mesh模型，以及顺便渲染出来的新视角影像。
3.1 什么是SDF
有向距离场的定义如下。
简单来说就是，对于空间中的点，计算它距离最近表面的距离。如果在表面内就为负，表面外就为正。需要注意的是SDF它是一种思路与方法，它不仅仅可以用于场景的三维表示，还可以用于字体渲染等领域。
在SDF领域，有个DeepSDF的工作，如上图所示。其主要内容就是通过深度网络来给出空间中某个点的SDF的值。NeRF的网络结构设计在一定程度上就是受这个网络的启发。
3.2 如何用SDF建模
上面，我们介绍了什么是SDF，那么如何用SDF来进行重建呢？不妨先回忆一下NeRF的训练过程。我们得到一个密度场和一个颜色场，然后利用渲染方程，得到合成的图像，并将其与真值做Loss，不断迭代，减小误差。这是比较容易理解的。但前面也说了，基于密度场的重建效果是比较差的。进一步，我们能不能把NeRF流程里的密度场替换成SDF场呢？如果可以的话，那么我们就可以基于SDF得到质量较高的三维模型了。这样想法没错。但是如果真的这样替换的话又会有新的问题。直观来说，NeRF输出的2D影像就是基于密度和颜色渲染出来的。你现在直接把密度场给丢掉了，还怎么渲染影像呢？能不能把积分公式中的密度换成SDF呢？不行，因为NeRF中对密度进行积分是有物理意义的。所以这个问题的核心是，我们如何找到一种转换，把SDF转换成NeRF中的密度。如果可以的话，就可以继续使用NeRF的框架，并且还可以得到SDF。一个可用的工作就是NeuS，将密度场和有向距离场联系起来，如上图所示。
首先，我们可以模仿一下渲染方程里的密度函数σ，我们也找一个概率密度函数把SDF表示起来。在论文中，作者选用了一个Logistic的分布函数，它是Sigmoid函数的导数。事实上，我们可以选择不同的概率密度函数，只要它是单峰的、且以0为中心就可以了。进一步，对于体积渲染方程，我们可以简化成上图中最下面公式的样子。把T(t)和σ(r(t))变成一个权重w(t)。这样的意义就是，我们把某个像素最终的渲染结果看做是由某条光线上所有采样点的颜色加权求和得到(这里我们把密度作为权重的一部分了)。进一步我们思考这个权重应该具备什么性质？至少有两个：第一是无偏的。无偏是指在最合适的地方有最合适的值。举个例子，某条光线穿过一个表面。那么这个像素的颜色应该由在这个表面的那一点的颜色决定，权重最高。但如果还没到表面点的时候，权重就很大了，这显然就是不合适的。第二是可以反应遮挡的。举个例子，空间中有一个球体，一条光线穿过它，显然会有两个点(入射点和出射点)。从SDF而言，这两个点的SDF值都为0。但从渲染的角度，显然是里我们最近的那个点应该具有最大的权重，而不是远处的那个点，或者两个点等权。
基于上面提到的两点，我们寻找最优的权重的表示，如上图所示。一个简单的想法是，我们把SDF外面套一个Logistic分布，就可以得到新的σ(t)。然后以此组成新的权重w(t)。这样其实得到的是有偏的权重，如右图左边部分所示。蓝色表示SDF函数，在物体表面时，SDF=0。由于我们选用的又是Logistic分布，所以概率密度应该如红色曲线所示。看起来还不错。但如果我们把这个σ(t)函数积分出来，就会发现这个权重在还没有到达表面的时候就已经到达了峰值。这显然就是有偏的。所以在NeuS工作中，首先将Logistic积到了Sigmoid函数，然后利用它作为权重。如上图中右边所示。可以看到，当在物体表面的时候，w(t)有最大值，也就是最大权重，这是一个无偏的表示。进一步，可以对比NeRF和NeuS的渲染方程如下。
NeuS采用的Loss如下。
此外，上图中可以看到NeuS和NeRF的对比。NeuS比NeRF更加光滑、干净的三维结果。事实上，上面说的这些，核心的思路还是寻找密度和SDF之间的关联，找到这种关联以后，就可以把SDF应用到NeRF的框架中去。所以，NeuS是一种办法，当然也会有其它办法，如下图所示。
比如VolSDF利用拉普拉斯分布表示密度和SDF之间的变换。Unisurf则是采用Occupancy Field，而不是SDF。此外，除了关注前景，我们还可以同时关注背景，这方面的工作是NeRF++。通过将前景放到圆里，背景放到圆外，分别训练两个模型来分别合成。
4.Practice
本节课的主要内容还是承接上节课的NeRF。一方面介绍了NeRF的一些不足之处，并给出了一些加速的策略与方法。另一方面是，在NeRF的框架里面，相比于单张合成影像，我们希望可以得到场景的更好的表示，如Mesh等。所以我们引进了相比于密度更好的表示，也就是SDF，并且研究了如何通过变换把密度和SDF关联起来，使其可以纳入NeRF框架。最终实现在只有2D影像+位姿的情况下，就可以输出一个比较好的三维的Mesh模型。
本文作者原创,未经许可不得转载,谢谢配合
