在SLAM中介绍旋转向量的时候会提到一个公式叫罗德里格斯公式(Rodrigues’ Formula)，它说明了旋转向量与旋转矩阵之间的关系。 假设某个旋转的旋转轴为向量\mathbf{n}，角度为θ。从旋转向量到选择矩阵可表示如下。
R=cos\theta \mathbf{I}+(1-cos\theta)\mathbf{nn}^{T}+sin\theta \mathbf{n}^{\times }\mathbf{n}^{\times }表示对向量\mathbf{n}取反对称矩阵。下面就对公式进行推导。
1.公式推导
本文的示意图来自Wiki上的罗德里格斯公式词条，点击查看。
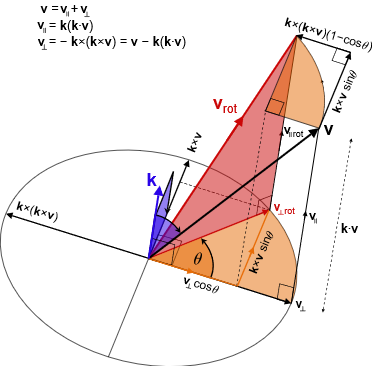
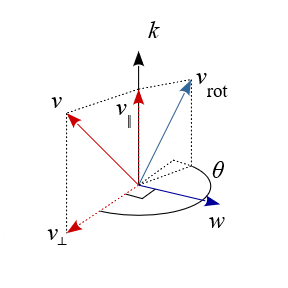如上图所示(点击图片可查看svg矢量图)，假设某个单位向量\mathbf{k}，某个向量\mathbf{v}以\mathbf{k}为轴，旋转了θ角(逆时针)变成了v_{rot}。对于\mathbf{v}，可以将其分解为垂直和平行于旋转轴k的分量v_{⊥}和v_{∥}，且根据向量加法满足如下关系。
对于v_∥由于其大小可以看成是向量\mathbf{v}在\mathbf{k}上的投影，即\mathbf{v}和\mathbf{k}做点积，而其方向与\mathbf{k}平行，可以表示成\mathbf{k}的倍数，因此可以表示成如下形式：
v_∥=(k\cdot v)k对于v_⊥，由上面的式子可以得到：
v_⊥=v-v_∥=v-(k\cdot v)k
而又如上图所示(点击图片可查看svg矢量图)，v_⊥等于-k×(k×v)。在上图中k×v得到的是一个垂直于\mathbf{k}、\mathbf{v}所构成平面的一个向量(可以看作是v_⊥绕k逆时针转90°)，方向满足右手定则(从\mathbf{k}转到\mathbf{v})。而\mathbf{k}再与k×v做叉乘，得到的是一个垂直于\mathbf{k}和k×v平面的向量(可以看作是v_⊥绕k逆时针转180°)，方向满足右手定则(从\mathbf{k}转到k×v)。所以k×(k×v)和v_⊥大小相等，方向相反，前者加个负号，即相等。因此：
v_⊥=v-v_∥=v-(k\cdot v)k=-k×(k×v)向量\mathbf{k}在绕\mathbf{k}旋转之后，其在旋转轴上的投影向量是不会变的(很容易理解，要不然也不叫旋转轴了)，有：
v_{∥rot}=v_∥对于垂直于\mathbf{k}轴的分量，只会改变方向，大小并不会变。
|v_{⊥rot} |=|v_⊥ |而由上图，根据三角函数知识，在直角三角形中可以计算出：
v_{⊥rot}=cosθv_⊥+sinθk×v_⊥因为\mathbf{k}与v_∥平行，所以它们做叉乘结果为\mathbf{0}向量，且根据\mathbf{v}与投影分量的关系，有：
k×v_⊥=k×(v-v_∥)=k×v-k×v_∥=k×v所以v_{⊥rot}可以写成：
v_{⊥rot}=cosθv_⊥+sinθ(k×v)因此对于旋转后的向量v_{rot}，有：
\begin{align} v_{rot} &=v_{\parallel rot}+v_{\perp rot} \\ &=v_{\parallel}+cos\theta v_{\perp}+sin\theta (k\times v) \\ &= v_{\parallel}+cos\theta (v-v_{\parallel})+sin\theta (k\times v) \\ &= cos\theta v+(1-cos\theta) v_{\parallel}+sin\theta (k\times v) \\ &= cos\theta v+(1-cos\theta) (k\cdot v)k+sin\theta (k\times v) \\ \end{align}即：
v_{rot}=cosθv+sinθ(k×v)+(1-cosθ)(k\cdot v)k以上为罗德里格斯的矢量运算表达式，下面推导矩阵运算形式。对于向量可以获得它对应的反对称矩阵K，
K=\begin{bmatrix} 0 & -k_z & k_y\\ k_z & 0 & -k_x\\ -k_y & k_x & 0 \end{bmatrix}=\mathbf{k}^{\times}所以有如下式子成立
Kv=k×v\\ K^2 v=k×(k×v)又因为v-v_∥=-k×(k×v)，所以v_∥=v+k×(k×v)，带入v_{rot}有：
\begin{align} v_{rot}&=cosθv+(1-cosθ) v_∥+sinθ(k×v)\\ &=cosθv+(1-cosθ)(v+k×(k×v))+sinθ(k×v) \end{align}整理可得：
\begin{align} v_{rot}&=v+K^2 v-cosθK^2 v+sinθKv\\ &=v(I+K^2-cosθK^2+sinθK) \end{align}一般把等式右边括号中的部分叫做旋转矩阵R，即：
R=I+(1-cosθ)K^2+sinθK又由于
K^2 v=k×(k×v)=-(v-(k\cdot v)k)所以整理可得：
K^2=kk^T-I带入上式，整理可得：
R=cosθI+(1-cosθ)kk^T+sinθk^{\times}这样便推导出了罗德里格斯公式。
本文作者原创,未经许可不得转载,谢谢配合
