基于Python的OpenCV图像处理14

• 模板匹配
  • 简介
  • 匹配步骤
  • 匹配算法
    • 平方差匹配(TM_SQDIFF)
    • 标准平方差匹配(TM_SQDIFF_NORMED)
    • 相关匹配(TM_CCORR)
    • 标准相关匹配(TM_CCORR_NORMED)
    • 相关匹配(TM_CCOEFF)
    • 标准相关匹配(TM_CCOEFF_NORMED)
  • OpenCV实现
  • 多对象匹配

模板匹配

简介

模板匹配顾名思义就是给定一幅影像(模板)然后在另一幅 图像中寻找这个模板的操作。它是一种用来在一幅大图中 寻找模板图像位置的方法。在OpenCV中有cv2.matchTemplate() 函数供我们方便调用。它的工作原理与2D卷积函数一样， 将模板图像在输入图像(大图)上滑动，并且在每一个位置对 模板图像和与其对应的输入图像的子区域进行比较。返回 的结果是一个灰度图像，每一个像素值表示了此区域与模板 的匹配程度。

匹配步骤

• 1.输入原图像(I)和模板图像(T)。在原图像中我们希望找到一块和模板匹配的区域
• 2.通过将模板在原图像上滑动来寻找最匹配的区域。 这里所谓的滑动是指模板图像块一次移动一个像素(从左往右，从上往下)。 在每一个位置，都进行一次度量计算，来判断该像素对应的原图像的特定区域 与模板图像的相似度。
• 3.对于模板T覆盖在I上的每个位置，把上一步计算的度量值保存在结果图像矩阵R中。 在R中每个位置都包含对应的匹配度量值。
• 4.在结果图像矩阵中寻找最值(最大或最小，根据算法不同而不同)。最值所对应的像素的位置即认为是最高的匹配。 以该点为顶点，长宽和模板大小图像一样的矩阵认为是匹配区域。在OpenCV中可以用cv2.minMaxLoc()函数获得最值坐标。

匹配算法

上面说了模板匹配的核心步骤。可以发现在步骤中有个核心问题。 那就是如何度量匹配程度，如何进行度量计算。在OpenCV中提供了 6中不同方法。这里就以这6种算法为基础介绍匹配算法。在下列公式中， \(T(x,y)\)表示模板，\(I(x,y)\)表示原图像，\(R(x,y)\)表示模板与原图相似度函数。 x、y表示某个像素，x’、y’表示循环变量，在模板那么大的范围内进行循环。

平方差匹配(TM_SQDIFF)

将模板中的像素依次与对应原图中的区域作差再平方求和，得到R。匹配越好，差值越小，R值越小。

标准平方差匹配(TM_SQDIFF_NORMED)

这个公式其实是对图像和模板进行了标准化操作，这样可以保证当模板和图像各个像素的亮度都乘上同一个系数时，相关度不变。 即当I(x,y)和T(x,y)变成kI(x,y)和kT(x,y)时，相关系数还是R(x,y)。与上面一样，匹配越好，R值越小。

相关匹配(TM_CCORR)

这类方法采用模板和图像间的乘法操作，所以较大的数表示匹配程度较高，0标识最坏的匹配效果。

标准相关匹配(TM_CCORR_NORMED)

这种方法和第二种类似，同样是通过标准化从而去除了亮度线性变化对相似度计算的影响。匹配越好R值越高。

相关匹配(TM_CCOEFF)

虽然也叫做相关匹配，但是和上面的还是有点不同。不同之处在于，把原图和模板都减去了各自的平均值。

匹配越好，R值越大。1表示完美匹配，-1表示糟糕的匹配，0表示没有任何相关性(随机序列)。

标准相关匹配(TM_CCOEFF_NORMED)

相比于上一个方法，这里又除了各自方差。经过减去平均值和除以方差这么两步操作之后， 无论是我们的待检图像还是模板都被标准化了， 这样可以保证图像和模板分别改变光照亮不影响计算结果。

匹配越好，R值越大。1表示完美匹配，-1表示糟糕的匹配，0表示没有任何相关性(随机序列)。

OpenCV实现

如果输入图像大小是（W × H），模板大小是（w × h），输出结果大小就是（W-w+1， H-h+1）。 当得到这幅图之后，就可以使用函数cv2.minMaxLoc()来找到其中最小值和最大值位置了。 第一个值为矩形左上角的点（位置），（w，h）为模板矩形的宽和高。这个矩形就是找到的模板区域了。 下面是实例代码：

# coding=utf-8
import cv2
from matplotlib import pyplot as plt

# 依次读取原图与模板
img = cv2.imread("E:\\p.jpg")
template = cv2.imread("E:\\t.jpg")

# 依次获取模板的宽高，用于后续绘制矩形
h = template.shape[0]
w = template.shape[1]

# 调用匹配函数
# 第一个参数是原图
# 第二个参数是模板
# 第三个参数是匹配算法
# 返回的结果是一个二维的float类型的数组,大小为W-w+1 * H-h+1
res = cv2.matchTemplate(img, template, cv2.TM_CCOEFF)

# 获取返回结果中最值及其在res中的位置
min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(res)

# 构造矩形并在原图上绘制
top_left = max_loc
bottom_right = (top_left[0] + w, top_left[1] + h)
cv2.rectangle(img, top_left, bottom_right, (255, 255, 255), 2)

# 在使用Matplotlib显示之前，需要调整BGR的顺序
b = img[:, :, 0]
g = img[:, :, 1]
r = img[:, :, 2]
img = cv2.merge((r, g, b))

# 打印相关信息
print img.shape
print template.shape
print res.shape
print res.dtype
print cv2.minMaxLoc(res)

# 利用Matplotlib绘图对比
plt.subplot(121), plt.imshow(res, cmap='gray')
plt.subplot(122), plt.imshow(img, cmap='gray')
plt.show()

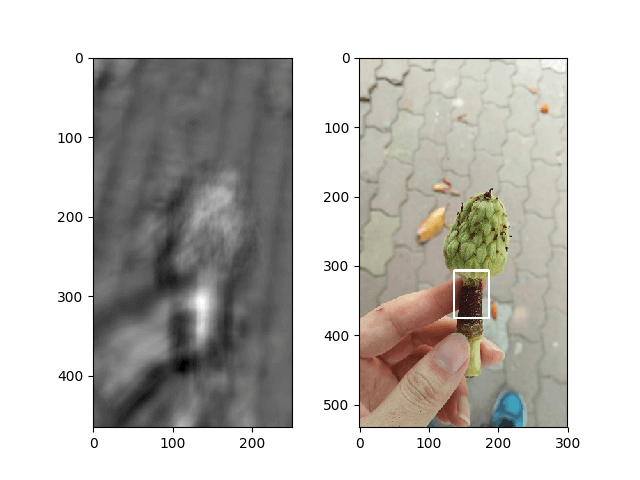
选择的原图与模板如下所示： 效果如下所示： 左边是返回的R值矩阵，最亮的那点被认为是最匹配的点。同时仔细观察便会发现，两幅影像的大小是不同的。 打印输出的信息如下： 可以看到是符合我们之前说的W-w+1、H-h+1的规律的。 利用这个方法可以比较好地找到图像中的指定区域。但在这个例子中也有一些问题。一个关键的问题就是模板中物体的大小 必须要和原图中对应物体的大小相同，否则就无法正确找到。下图是缩小了模板大小后的结果，可以发现结果是错的。 此外还要注意在绘制res时，不能使用cv2.imshow()，因为res超过了显示范围，发生截断，绘制出来的图像会不对，如下所示： 解决办法的方法有两个。一是利用Matplotlib绘图，而是将匹配算法改成对应标准化的，使R的范围在-1到1之间。下图是标准化后 利用OpenCV绘制的图像： 用标准化方法的好处是R的范围是已知的，更利于进行判断等操作。而非标准化方法由公式就可以看出来，其计算量少一些，会稍微快一些。 所以针对不同用途可以选择是否采用标准化方法。

多对象匹配

在上面的例子中，原图中只出现了一次模板中的对象，但有时更有可能一幅图像中出现多个模板对象，这时就需要多对象匹配了。 在OpenCV中cv2.minMaxLoc()只会返回最值的位置。所以显然现在不能使用这个函数了。我们需要设置一个阈值，当R值大于这个 阈值时，认为是模板对象，否则不是。所以这里显然用标准化的方法更加合适，否则我们无法确定阈值。代码如下：

# coding=utf-8
import cv2
from matplotlib import pyplot as plt
import numpy as np

# 依次读取原图与模板
img = cv2.imread("E:\\img.png")
template = cv2.imread("E:\\house.png")

# 依次获取模板的宽高，用于后续绘制矩形
h = template.shape[0]
w = template.shape[1]

# 调用匹配函数
# 第一个参数是原图
# 第二个参数是模板
# 第三个参数是匹配算法
# 返回的结果是一个二维的float类型的数组,大小为W-w+1 * H-h+1
res = cv2.matchTemplate(img, template, cv2.TM_CCOEFF_NORMED)

# 设定阈值
threshold = 0.8

# 从res中提取大于阈值的像素的位置
loc = np.where(res >= threshold)

# 遍历不同位置，绘制矩形
# 在函数调用中使用*list/tuple，表示将list/tuple分开，作为位置参数传递给对应函数（前提是对应函数支持不定个数的位置参数）
# 切片[::-1]是将列表或字符倒过来
for pt in zip(*loc[::-1]):
    cv2.rectangle(img, pt, (pt[0] + w, pt[1] + h), (0, 0, 255), 2)

# 在使用Matplotlib显示之前，需要调整BGR的顺序
b = img[:, :, 0]
g = img[:, :, 1]
r = img[:, :, 2]
img = cv2.merge((r, g, b))

# 利用Matplotlib绘图对比
plt.subplot(121), plt.imshow(res, cmap='gray')
plt.subplot(122), plt.imshow(img, cmap='gray')
plt.show()

输入的模板与原图如下： 匹配结果如下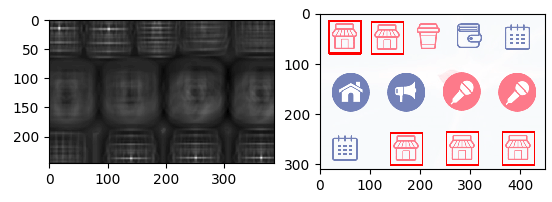： 可以看到较好地识别出了所有的相同目标。当然和之前说的一样，还是存在着尺度问题。一旦模板对象大小和图片中的对象 大小不同，识别就会有错误。
下面是对一幅真实的遥感影像进行模板匹配的例子。选择的模板和原图如下，阈值选择为0.8。 代码如下：

# coding=utf-8
import cv2
from matplotlib import pyplot as plt
import numpy as np

img = cv2.imread("E:\\sate_img.png")
template = cv2.imread("E:\\dot.png")

h = template.shape[0]
w = template.shape[1]

res = cv2.matchTemplate(img, template, cv2.TM_CCOEFF_NORMED)

# 设定阈值
threshold = 0.8

# 从res中提取大于阈值的像素的位置
loc = np.where(res >= threshold)

# 遍历不同位置，绘制矩形
for pt in zip(*loc[::-1]):
    cv2.rectangle(img, pt, (pt[0] + w, pt[1] + h), (0, 0, 255), 1)

b = img[:, :, 0]
g = img[:, :, 1]
r = img[:, :, 2]
img = cv2.merge((r, g, b))

# 利用Matplotlib绘图对比
plt.subplot(121), plt.imshow(res, cmap='gray')
plt.subplot(122), plt.imshow(img, cmap='gray')
plt.show()

匹配结果如下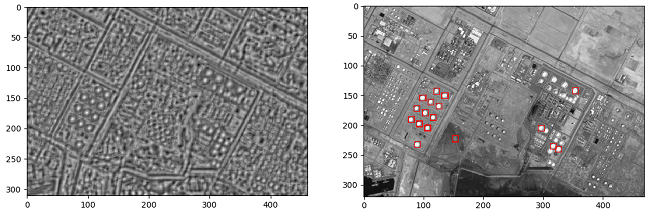： 可以看到比较好地识别出了我们选择的模板对象。但是有多选的非对象。造成这种情况的原因是影像中有很多相似的地物， 所以导致相似度很高，我们可以通过提高阈值来提升正确率。下图是阈值为0.85时的结果。 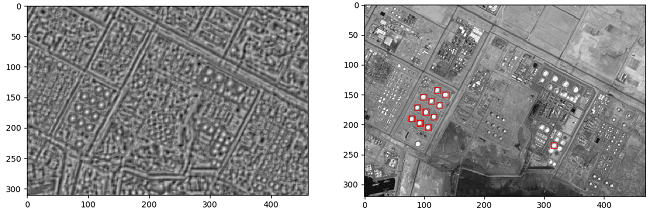下图动态展示了阈值的变化对于匹配结果的影响。