一、二值图像距离变换
图像距离变换是二值化图像处理与操作中的常用手段， 其主要思想是通过标识空间点(目标点与背景点)距离，将二值化图像转换为灰度图像。 可用于骨架提取、图像窄化等等。它的结果是得到一张与输入影像类似的灰度图像， 但是灰度值只出现在前景区域，并且离物体边缘越远的像素灰度值越大。
1.主要过程
- 1.将图像中的目标像素点分类，分为内部点、外部点和孤立点。
以中心像素的四邻域为例，如果中心像素为目标像素(值为1)且四邻域都为目标像素(值为1)，
则该点为内部点。如果该中心像素为目标像素，四邻域为背景像素(值为0)，则该中心点为孤立点，如下图所示。
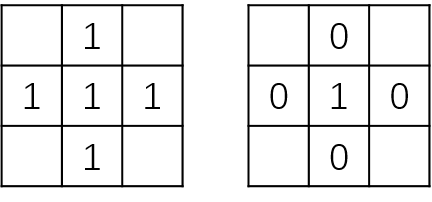除了内部点和孤立点之外的目标区域点为边界点。 - 2.统计图像中所有的内部点和非内部点，分别用S1、S2表示。
- 3.对于S1中的每个内部点P(x,y)，使用距离计算公式dist()计算其与S2中所有点的最小距离。每一个点对应一个最小距离， 这些最小距离构成集合S3。
- 4.计算S3中的最大值Max、最小值Min。
- 5.对于S1中的所有内部点，其对应灰度按下式计算：
S3(x,y)表示(x,y)对应的像素与S2中所有点的最短距离。
- 6.对于孤立点灰度值保持不变。
2.距离变换算法
在上面步骤中，提到了计算距离的函数dist()，这便是不同算法体现之处。按照变换类型可以分为欧式距离变换和非欧式距离变换两种。 非欧式距离变换包括棋盘距离变换、城市街区距离变换、倒角距离变换等。主要算法公式如下：
(1)欧氏距离
\[dist((x_{1},y_{1}),(x_{2},y_{2}))=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}\](2)曼哈顿距离
\[dist((x_{1},y_{1}),(x_{2},y_{2}))=\left | x_{1}-x_{2} \right |+\left | y_{1}-y_{2} \right |\](3)切比雪夫距离
\[dist((x_{1},y_{1}),(x_{2},y_{2}))=max(\left | x_{1}-x_{2} \right |,\left | y_{1}-y_{2} \right |)\]3.OpenCV实现
在OpenCV中有方便的cv2.distanceTransform()用于实现距离变换。代码如下：
# coding=utf-8
from matplotlib import pyplot as plt
import numpy as np
import cv2
# 以灰度模式读取图像
img = cv2.imread("E:\\dist.png", 0)
# 设置阈值进行二值化
# 注意这里二值化的同时对图像进行了反色，因为背景比前景颜色要浅，
# 直接二值化的结果是背景是白色的，前景是黑色的，这显然不是我们想要的结果
# 同时注意这样两个操作相加的这种写法
ret, binary = cv2.threshold(img, 0, 255, cv2.THRESH_OTSU + cv2.THRESH_BINARY_INV)
# 调用距离变换函数
# 第一个参数是二值化图像
# 第二个参数是类型distanceType
# 第三个参数是maskSize
# 返回的结果是一张灰度图像，但注意这个图像直接采用OpenCV的imshow显示是有问题的
# 所以采用Matplotlib的imshow显示或者对其进行归一化再用OpenCV显示
dist = cv2.distanceTransform(binary, cv2.DIST_L2, 5)
# 将灰度、二值化图像合并到一个窗口中显示
result = np.hstack((img, binary))
cv2.imshow("result", result)
plt.imshow(dist, cmap='gray')
plt.show()
cv2.waitKey(0)
效果如下：
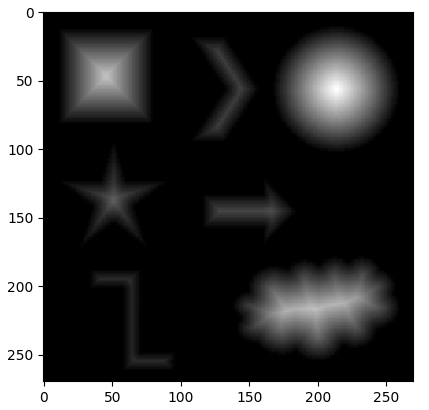可以看到，通过距离变换的图像越靠近物体中心的地方越亮。
二、灰度三维模型
在介绍分水岭法之前，先介绍图像的另一种表达形式，灰度三维模型。简单来说就是把某个像素的灰度值当作高程，
图像的宽高为x、y轴，这样就可以做出一个三维模型。例如有一幅图像如下所示：
我们以灰度为高程，可以做出如下图形：
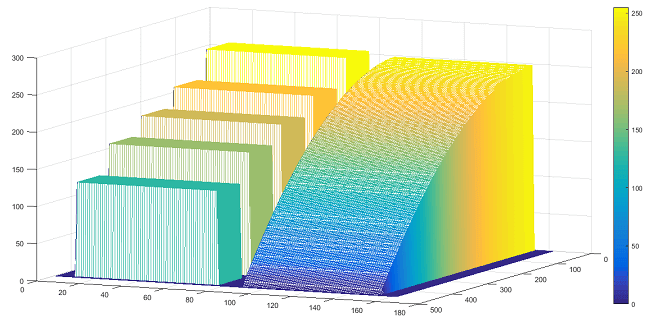可以看到，图中蓝色越深的地方表示灰度值越低，越黄的地方表示灰度值越高。该图是采用Matlab绘制的。代码非常简单。
function [] = Draw3DGray( path )
%将RGB图像转换成对应的灰度图像并以各像素灰度数值画出3D模型
% 例如输入文件路径为：E:\p1.png
I = imread(path);
GrayScaleImage = rgb2gray(I);
mesh(GrayScaleImage);
end
那么在Python下如何绘制呢，这是我们下面讨论的问题。
1.绘制图像的灰度三维模型
代码如下：
# coding=utf-8
from matplotlib import pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import cv2
img = cv2.imread("E:\\color.png", 0)
fig = plt.figure()
ax = Axes3D(fig)
X = np.arange(0, img.shape[0], 1)
Y = np.arange(0, img.shape[1], 1)
X, Y = np.meshgrid(X, Y)
Z = img[X, Y]
# 具体函数方法可用 help(function) 查看
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
cv2.imshow("img", img)
plt.show()
cv2.waitKey(0)
在代码中用到了Matplotlib以及绘制三维图像的库。效果如下：
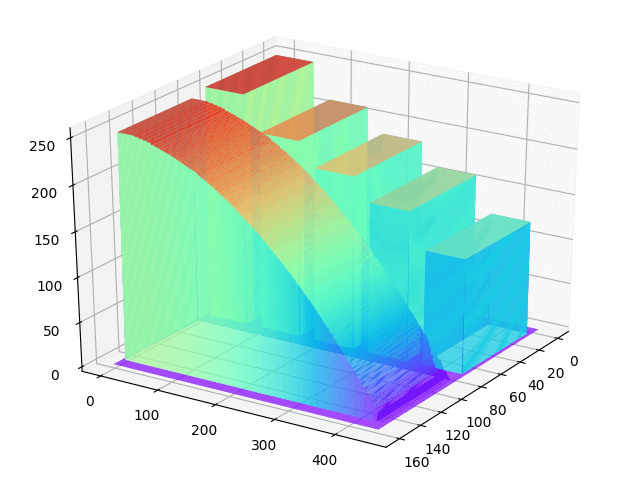下面的动图更好地展示了三维灰度模型的效果。这里为了绘制更快，将行列的采样间隔设置为6，以减少绘制的点数。
仔细观察边缘会发现精度有一定损失。
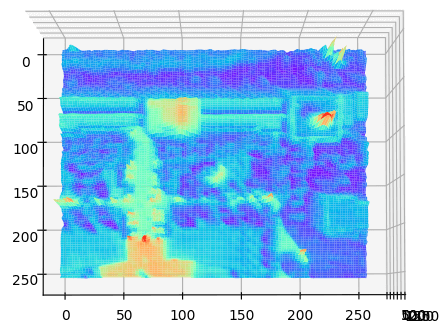
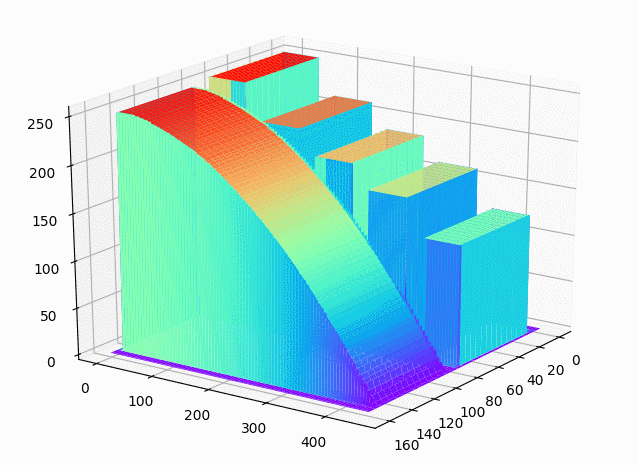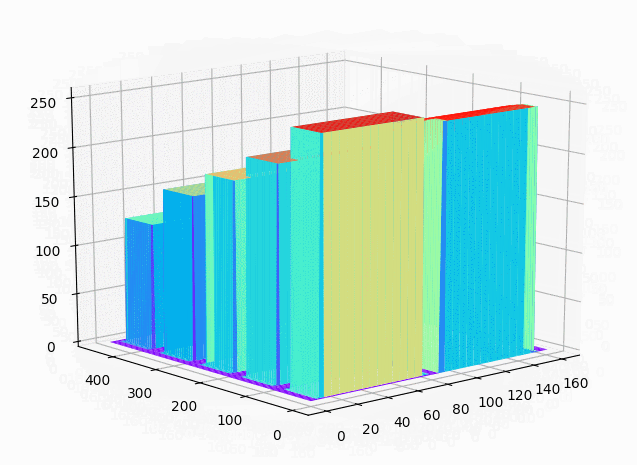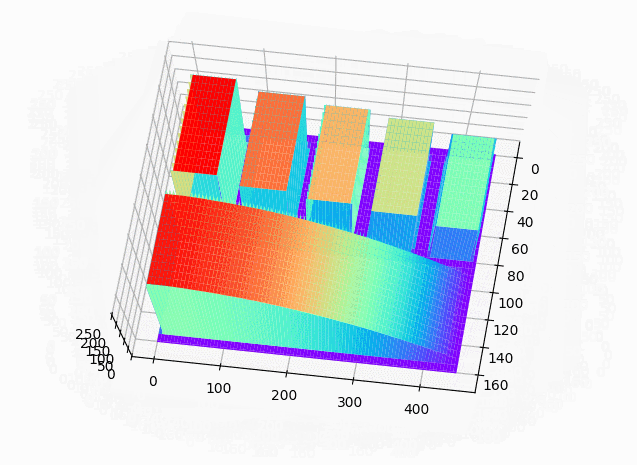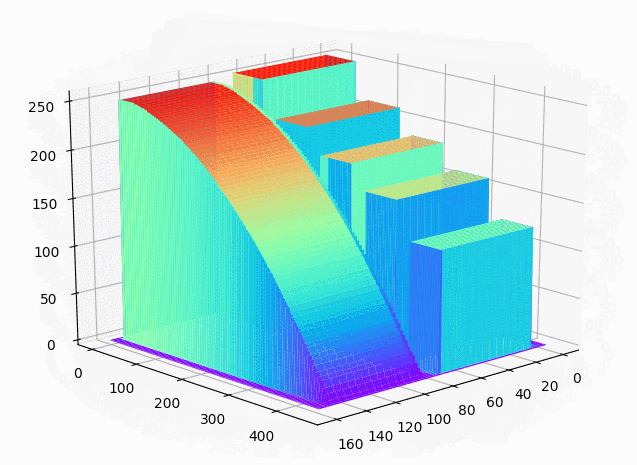下图是对一块真实地物进行绘制的效果。原图如下：
三维灰度地形图如下：
三、图像梯度
图像梯度和数学上的梯度其实是类似的，可以用一阶导数或二阶偏导数求解。 沿梯度方向导数变化量达到最大值，也就是说，梯度的方向是函数在这点变化最快的方向。 反映的是图像灰度在某点的变化，梯度越大表示变化越明显。 但是图像以矩阵的形式存储的，不能像数学理论中对直线或者曲线求导一样， 对一幅图像的求导相当于对一个平面、曲面求导。对图像的操作， 采用模板对原图进行卷积运算，从而达到想要的效果。 而获取一幅图像的梯度就转化为：模板（Roberts、Prewitt、Sobel、Lapacian算子）对原图像进行卷积。
1.推导过程
(1)Roberts算子
在一维连续数集上求导，有如下公式：
\[{f}'(x)=\frac{f(x+ \Delta x)-f(x)}{\Delta x}\]在二维连续数集上，在x、y方向有偏导数，公式如下：
\[\frac{\partial f(x,y)}{\partial x}=\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}\] \[\frac{\partial f(x,y)}{\partial y}=\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}\]在某点的梯度为一矢量，如下：
\[grad(f)=\left ( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right )\]其对应的梯度的大小为：
\[\left | grad(f) \right |=\sqrt{\left ( \frac{\partial f}{\partial x} \right )^{2}+ \left ( \frac{\partial f}{\partial y} \right )^{2}}\]而在二维离散数集上，令\(\Delta x =1\)、\(\Delta y =1\)则可得到对应离散情况下的公式，也可以为2，只是表示一个单位的度量。 因此对于图像而言，其偏导数以及梯度公式如下：
\[g_{x}=\frac{\partial f(x,y)}{\partial x}=f(x+1,y)-f(x,y)\] \[g_{y}=\frac{\partial f(x,y)}{\partial y}=f(x,y+1)-f(x,y)\] \[\left | grad(f) \right |=\sqrt{g_{x}^{2}+ {g_{y}^{2}}}\approx \left | g_{x}^{2} \right |+\left | g_{y}^{2} \right |\]因此，在x方向，由偏导公式可知，其实就是相邻两个像素的值相减。同理，y方向也是如此。因此可以得到如下算子。
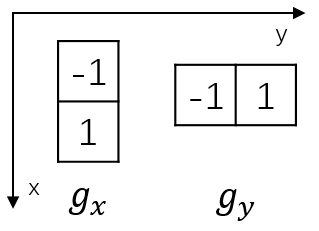类似地，对于对角线方向梯度，公式和算子如下：
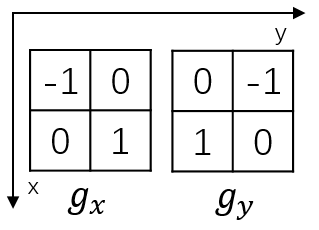上述算子为Robert算子。
(2)Prewitt算子
2×2模板在概念上很简单，但是对于计算边缘方向不是很有用。一般模板最小为3×3。
在3×3模板中，定义图像梯度如下：
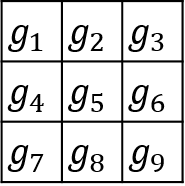
以上公式对应的算子如下：
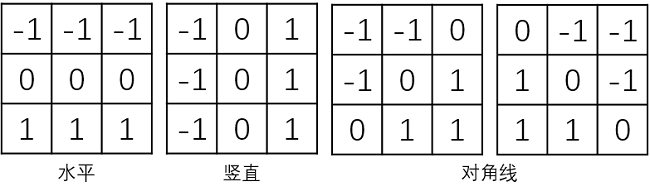这些算子称为Prewitt算子。
(3)Sobel算子
Sobel算子是在Prewitt算子的基础上改进的，在中心系数上使用一个权值2， 相比较Prewitt算子，Sobel模板能够较好的抑制（平滑）噪声。
\[g_{x}=\frac{\partial f}{\partial x}=(z_{7}+2z_{8}+z_{9})-(z_{1}+2z_{2}+z_{3})\] \[g_{y}=\frac{\partial f}{\partial y}=(z_{3}+2z_{6}+z_{9})-(z_{1}+2z_{4}+z_{7})\]对应算子如下：
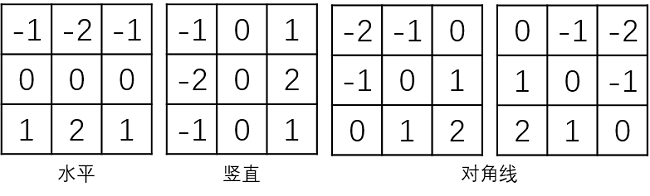
(4)Lapacian算子
上述所有算子都是通过求一阶导数来计算梯度的，通常用于边缘检测。 在图像处理过程中，除了检测线，有时候也需要检测特殊点，这就需要用二阶导数进行检测。 离散二阶导数计算公式如下：
\[\frac{\partial ^{2}f}{\partial x^{2}}=\frac{ {\partial}' f}{\partial x} \\={(f(x+1)-f(x))}' \\={f(x+1)}'-{f(x)}' \\=(f(x+2)-f(x+1))-(f(x+1)-f(x)) \\=f(x+2)-2f(x+1)+f(x)\]但我们想要的是x位置的偏导，因此x整体减一，得到：
\[\frac{\partial ^{2}f}{\partial x^{2}}=\frac{ {\partial}' f}{\partial x} \\={(f(x+1)-f(x))}' \\={f(x+1)}'-{f(x)}' \\=(f(x+2)-f(x+1))-(f(x+1)-f(x)) \\=f(x+2)-2f(x+1)+f(x)\] \[\frac{\partial ^{2}f}{\partial x^{2}}=f(x+1)-2f(x)+f(x-1)\]同理可以得到y的二阶导数。求梯度时使用拉普拉斯模板，即可以得到拉普拉斯算子计算公式：
\[\bigtriangledown ^{2}f(x,y)=\frac{\partial ^{2}f}{\partial x^{2}}+\frac{\partial ^{2}f}{\partial y^{2}} \\=[f(x+1,y)-2f(x,y)+f(x-1,y)]+[f(x,y+1)-2f(x,y)+f(x,y-1)] \\=f(x+1,y)+f(x,y+1)+f(x,y-1)+f(x-1,y)-4f(x,y)\]算子为：
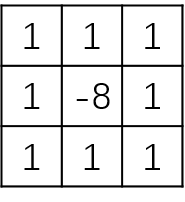模板中心位置的数字是-8而不是-4，是因为要使模板中的这些系数之和为0。
这样不至于改变原图的明暗程度。如果模板的系数大于0，则使用该模板处理完后，所有像素的灰度值都变大了，
直观反映就是图像变亮了。
在用Lapacian算子图像进行卷积运算时，当响应的绝对值超过指定阈值时，那么该点就是被检测出来的孤立点。
2.代码示例
如下代码计算x方向的Prewitt算子。
import cv2
import numpy as np
img = cv2.imread("E:\\jack_fruit.jpg")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
grad_x = np.matrix('-1,-1,-1;'
'0,0,0;'
'1,1,1')
grad_y = np.matrix('-1,0,1;'
'-1,0,1;'
'-1,0,1')
dst_x = cv2.filter2D(gray, -1, grad_x)
dst_y = cv2.filter2D(gray, -1, grad_y)
dst = cv2.add(dst_x, dst_y)
cv2.imshow("fruit", img)
cv2.imshow("dst", dst)
cv2.imshow("dst_x", dst_x)
cv2.imshow("dst_y", dst_y)
cv2.waitKey(0)
效果如下：
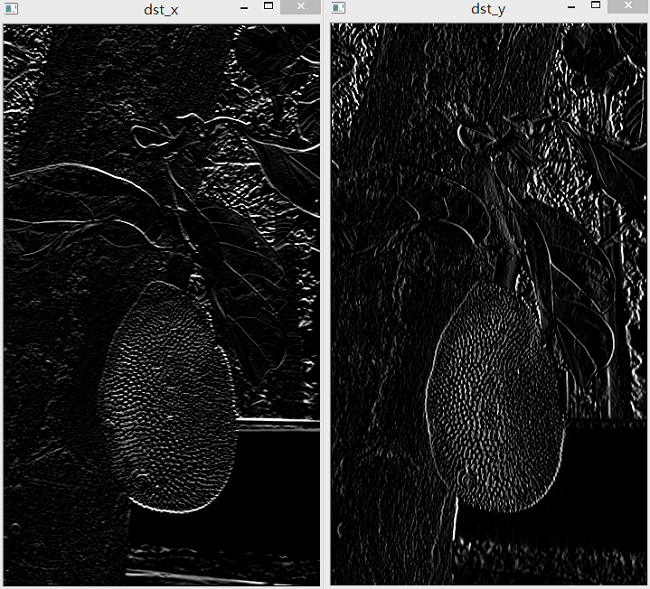
得到了x、y以及总的梯度图像。
四、分水岭算法图像分割
1.思路与原理
有了上面对图像灰度三维模型的直观感受，会更好理解分水岭算法的思想。
在分水岭算法中，一幅图像中灰度值高的区域被看作山峰，灰度值低的区域被看作山谷。
然后从山谷的最低点灌水，水会慢慢在不同的地方汇合，而这些汇合的地方就是需要对图像分割的地方。
分水岭算法的核心思想就是建立堤坝阻止不同盆地的水汇合。
在一般分水岭算法中，通常是把一副彩色图像灰度化，然后再求梯度图，
最后在梯度图的基础上进行分水岭算法，求得分段图像的边缘线。如下所示是一个“地形”的剖面示意图。
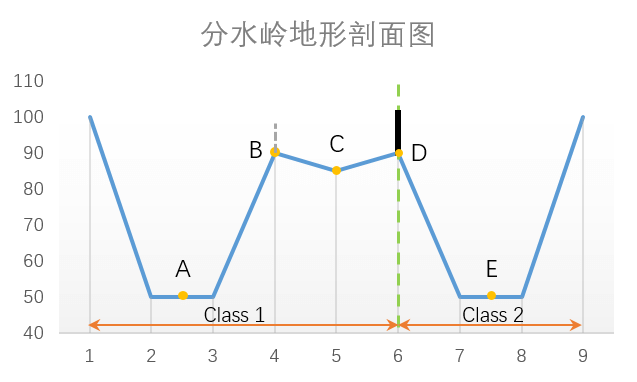以绿色虚线为界，左边表示地物1，右边表示地物2。A为地物1在当前范围内的最小值点，
E为地物2在当前范围内的最小值点，两个盆地的交汇点为D。在地物1中C为小范围内的极小值点。
首先在两个盆地的最小值点A、E开始向盆地中注水，水会缓慢上升。 在两个盆地的水汇集的时刻，在交接的边缘线上(D点所在位置，也即分水岭线)， 建一个堤坝(图中黑色线段)，来阻止两个盆地的水汇集成一片水域。 这样图像就被分成2个像素集，一个是注水盆地像素集，一个是分水岭线像素集。
但仔细观察就会发现问题，传统的基于图像梯度的分水岭算法由于存在太多极小区域而产生许多小的集水盆地， 带来的结果就是图像过分割。 如图C点所在的极小值区域会形成一个小盆地，从而让地物1被分成两部分， 当C盆地的水和A盆地的水要汇合时，会在B点建立个水坝(图中灰色虚线)， 这显然不是我们想要的结果。 所以必须对分割相似的结果进行合并。 举个例子如一个桌面的图片，由于光照、纹理等因素，桌面会有很多明暗变化，反映在梯度图上就是一个个圈， 此时利用分水岭算法就会出现很多小盆地，从而分割出很多小区域。但这显而易见是不符合常识的。 因为桌面是一个整体，应该属于同一类，而不是因为纹理而分成不同的部分。
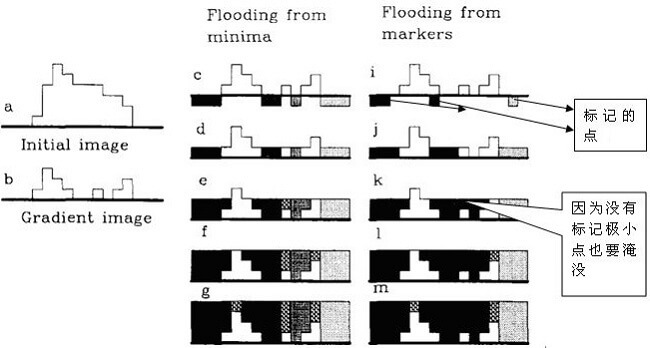
因此需要对分水岭算法进行改进。在OpenCV中采用的是基于标记的分水岭算法。
水淹过程从预先定义好的标记图像（像素）开始，
这样可以减少很多极小值点盆地产生的影响。
较好的克服了过度分割的不足。
本质上讲，基于标记点的改进算法是利用先验知识来帮助分割的一种方法。
对比如下图所示。
2.OpenCV实现
在OpenCV中实现分水岭算法可以使用cv2.watershed()函数实现，主要有以下步骤：
- 1.输入图像，对图像进行二值化
- 2.对二值化后的图像进行噪声去除
- 3.通过腐蚀、膨胀运算对图像进行前景、背景标注
- 4.运用分水岭算法对图像进行分割
从调用API的角度而言，在整个过程中并没有对原始影像求梯度，而是直接进行二值化， 进行像素标记。然后将标记图像与原图一起传入函数。 具体求梯度的操作封装在了函数中，用户无需关心。
具体实例如下，下面是待分割的影像。影像中有很多彼此连接的硬币，
我们需要将这些硬币彼此分开。
(1)读取图像进行二值化操作
img = cv2.imread("E:\\coins.jpg")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_OTSU + cv2.THRESH_BINARY_INV)
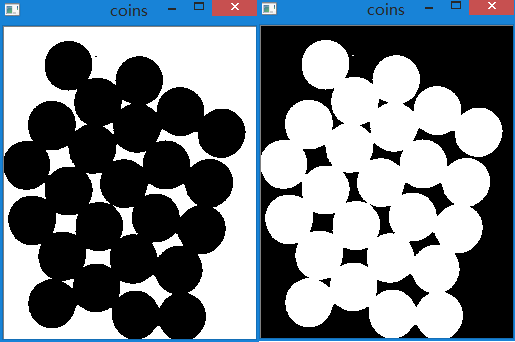
需要注意的是，由于这里前景比背景颜色深，所以需要在二值化后反色操作一下。
下图是反色前与反色后的效果，我们希望得到的是右边的效果(前景比背景亮)。
(2)对二值化图像进行噪声去除
kernel = np.ones((3, 3), np.uint8)
open = cv2.morphologyEx(thresh, cv2.MORPH_OPEN, kernel, iterations=2)
仔细观察二值化后的图像，会发现有一些噪声点。如果这些噪声点不去除，则在后续步骤中会被标记成前景或背景，
从而影响分割。由前面形态学知识可知，对于白噪声，如黑色背景中的小白点，可以使用开运算(先腐蚀后膨胀)去除，效果很好。
同理，对于硬币中的黑色小洞(白色背景中的小黑点)，可以使用闭运算(先膨胀后腐蚀)。
在这里主要是白噪声，硬币内部并没有空洞，因此只需要进行开运算即可。完成后效果如下。
(3)图像标记
在完成了前期工作后，就可以对图像进行标记了。简单说来，对图像进行标记主要是将图像标记成三个部分： 前景(物体)、背景以及未知区域。 我们现在知道靠近对象中心的区域肯定是前景，而远离对象中心的区域肯定是背景，不能确定的区域即是图像边界。 对于前景区域，可以在第二步得到的图像上进行多次腐蚀运算， 这样就可以得到肯定是前景的区域。同样，对该图像进行多次膨胀运算，可以得到比前景大的范围， 除去这些范围的部分肯定是背景。至于在两者之间的就是未知区域，也就是需要运用分水岭算法， 从而给出分水岭边界的地方。
a.前景标记
提取肯定是硬币的区域(前景)，可以使用腐蚀操作。腐蚀操作可以去除边缘像素，剩下就可以肯定是硬币了。 当硬币之间没有接触时，这种操作是有效的。但是由于硬币之间是相互接触的， 我们就有了另外一个更好的选择：距离变换再加上合适的阈值。
distance_transform = cv2.distanceTransform(open, 1, 5)
ret, sure_fg = cv2.threshold(distance_transform, 0.7 * distance_transform.max(), 255, cv2.THRESH_BINARY)
效果如下：
图中白色的部分我们可以肯定是硬币，也就是前景。
b.背景标记
背景标记相对简单。在开运算结果的基础上，对其进行多次膨胀。
sure_bg = cv2.dilate(open, kernel, iterations=3)
结果如下：
图中黑色部分肯定是背景。
c.未知区域
背景、前景对比图如下：
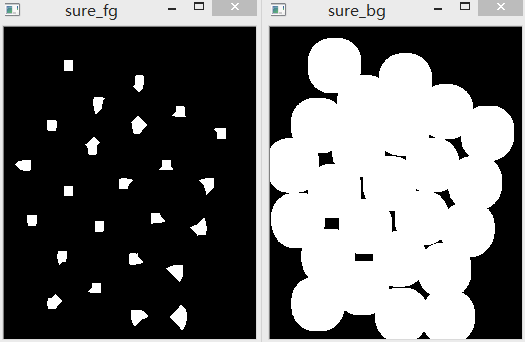所以可以用背景减去前景，就可以得到边界所在的范围，形成一个白色环。
sure_fg = np.uint8(sure_fg)
unknown = cv2.subtract(sure_bg, sure_fg)
需要注意的是，距离变换后获得的图像数据类型是float32，因此需要转成uint8才能和sure_bg做运算。
效果如下：
(4)创建标签
在知道了哪些肯定是前景区域后，就可以给它们创建标签了(一个与原图像大小相同，数据类型为int32的数组)。
对我们已经确定分类的区域（无论是前景还是背景）使用不同的正整数标记，对不确定的区域使用0标记。
我们可以使用函数cv2.connectedComponents()来完成。
它会把将背景标记为0，其它对象使用从1开始的正整数标记。
但我们知道如果背景标记为0，那分水岭算法就会把它当成未知区域了。
因此我们还需要对返回的结果进行一些修改，如统一加1或其它数字。
但这里不能减。因为OpenCV会把边界标记成负数。因此这里都使用正数。
在把背景和前景标记完后，最后是将未知区域标记为0。
ret, markers1 = cv2.connectedComponents(sure_fg)
markers = markers1 + 1
markers[unknown == 255] = 0
标记完成后，利用Matplotlib中Jet ColorMap显示效果如下：
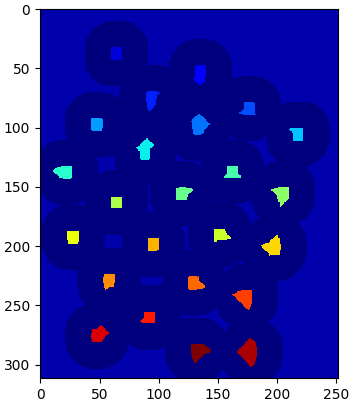深蓝色区域为未知区域。肯定是硬币的区域使用不同的颜色标记。其余区域就是用浅蓝色标记的背景了。
这里不能使用OpenCV的cv2.imshow()显示，否则效果如下：
原因是，由于每个像素的标记值都很小，而且彼此差异不大，所以在OpenCV中显示一片黑，灰度虽然和0有差别，但人眼几乎无法分辨。
所以不是理想的效果。如果要使用OpenCV显示，则需要先对标记影像进行拉伸，拉伸到0-255范围。
(5)实施分水岭算法
之前的工作都是为这一步做准备。这一步最核心，也最简单，代码如下：
markers3 = cv2.watershed(img, markers)
img[markers3 == -1] = [0, 0, 255]
分割效果如下：
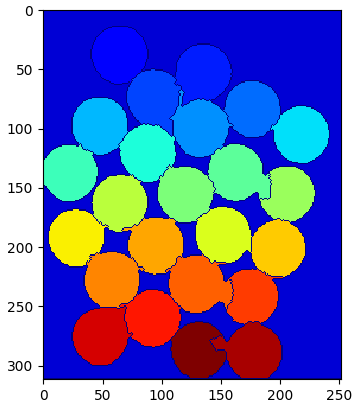
可以看到有些硬币边缘分割很好，有些不够好。
3.完整代码
# coding=utf-8
import cv2
import numpy as np
from matplotlib import pyplot as plt
# 打开影像
img = cv2.imread("E:\\coins.jpg")
# 转换为灰度图
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 阈值+反色操作
# 注意将两个操作放在一起的用法
ret, thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_OTSU + cv2.THRESH_BINARY_INV)
# 进行开运算操作，去除噪声
kernel = np.ones((3, 3), np.uint8)
open = cv2.morphologyEx(thresh, cv2.MORPH_OPEN, kernel, iterations=2)
# 膨胀操作获取背景
sure_bg = cv2.dilate(open, kernel, iterations=3)
# 距离变换+阈值获取前景
# 距离变换第一个参数是输入图像
# 第二个参数是距离类型
# 第三个参数是范围大小
distance_transform = cv2.distanceTransform(open, cv2.DIST_L2, 5)
# 注意获取某幅图像最大值max()的用法
ret, sure_fg = cv2.threshold(distance_transform, 0.7 * distance_transform.max(), 255, cv2.THRESH_BINARY)
# 背景、前景相减，得到未知区域
sure_fg = np.uint8(sure_fg)
unknown = cv2.subtract(sure_bg, sure_fg)
# 标记图像
ret, markers1 = cv2.connectedComponents(sure_fg)
markers = markers1 + 1
# 注意这种简便用法
# markers和unknown是规模相等的两个矩阵
# 如果unknown某个元素为255，则在markers对应位置上的元素赋为0
markers[unknown == 255] = 0
# 调用分水岭算法
markers3 = cv2.watershed(img, markers)
# 注意OpenCV读取的图像顺序是BGR
# OpenCV中将分水岭边界标记为-1
img[markers3 == -1] = [0, 0, 255]
# 展示结果
plt.imshow(markers3, cmap='jet')
cv2.imshow("result", img)
plt.show()
cv2.waitKey(0)
本文作者原创,未经许可不得转载,谢谢配合
