一、特征与特征点
1.特征点
所谓特征，可以理解为区别于其它部分或物体的地方。根据特征应该能准确、唯一地识别出对应目标。 例如在一堆青苹果中，有几个红苹果。那么红色就是可以准确识别出红苹果的有效特征。
人眼对特征的识别通常是在一个局部的小区域或小窗口完成的。
如果在各个方向上移动这个特征的小窗口，窗口内区域的灰度发生了较大的变化，那么就认为在窗口内遇到了特征点。
如果这个特定的窗口在图像各个方向上移动时，窗口内图像的灰度没有发生变化，那么窗口内就不存在特征点；
如果窗口在某一个方向移动时，窗口内图像的灰度发生了较大的变化，而在另一些方向上没有发生变化，
那么，窗口内的图像可能就是一条直线的线段。
如下图所示，蓝色区域是某个我们需要提取特征的目标。
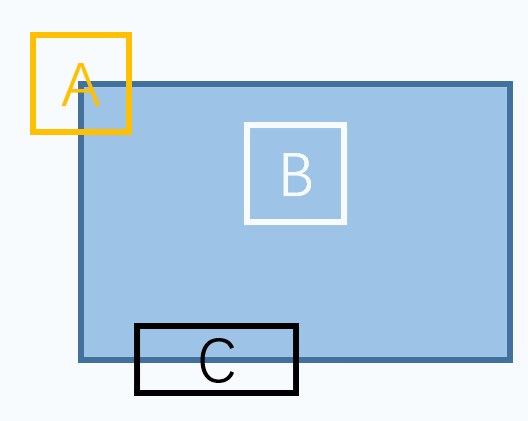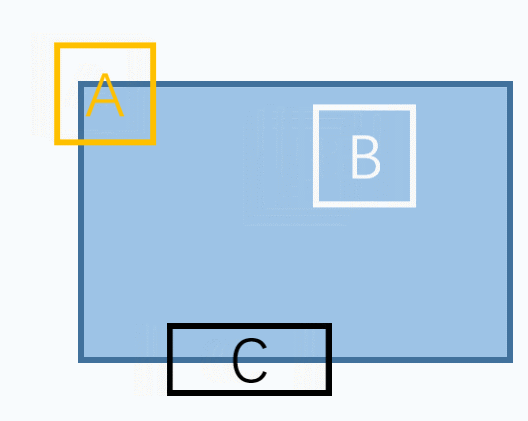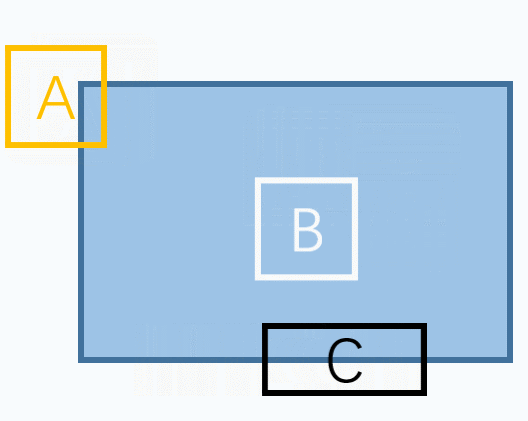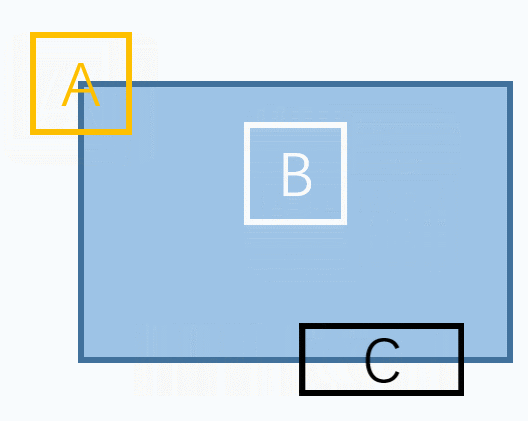我们可以选择很多种特征，如图分别选择了点、线、面三种特征。
但是会发现，对于B(面特征)来说，不管朝哪个方向移动，选择的内容都没有变化，很难被找到和跟踪，因此不能很好地作为特征描述。
对于C(线特征)在垂直于线的方向具有很好地辨别能力，但是在沿线方向却无法准确定位，因此也不是很好的特征描述。
这样，对于A(点特征)，可以发现无论是朝哪个方向移动，窗口对应的内容都会有很大的变化，是唯一的。
因此，这是理想的特征描述。所以基本上来说，角点是一个好的图像特征。当然不仅仅是角点，有些斑点也是好的图像特征。
2.特征检测
知道了如何唯一地表达特征，下面就是如何找到它。在前面的过程中其实已经有所涉及。很简单的想法是， 在一幅图像上滑动比较，如果无论往哪个方向移动，窗口内容变化都很大，那么这个地方一定是角点。 如果沿某一方向无明显变化，沿另一方向变化很大，说明很有可能是边缘。如果无论哪个方向都没有变化，则可能是内部或外部的面状目标。 这样我们就可以把一幅图像上的特征以特征点的方式提取出来了。
3.特征描述
在一幅图中找到特征后，我们自然希望在其它图中也找到同样的特征。因此我们需要对特征进行描述。
例如，如下图所示，三角形A是我们要找的特征，但是在图中有其它类似特征，因此需要对A进行描述。
如，在橙色矩形下面，绿色圆形右边，黑色五边形左边。这样就可以在其它图片中搜索相同区域，
根据这个表述就可以准确找到A三角形而不是B了。
因此，应用特征的一般步骤是使用各种算法来查找图像特征，然后描述它，最后对它们进行匹配。
二、图像中的角点
在图像中，角点是重要特征，对图像的理解和分析有很重要的作用。角点在保留图像重要特征的同时， 可以有效减少信息数据量，使其信息含量很高，有效提高了计算速度。这也就是为什么在做两幅影像的匹配配准之前， 需要先对图像提取特征点(角点)的原因。这样也使实时处理成为可能。 因此说角点在三维场景重建、运动估计、目标跟踪、目标识别、图像配准与匹配等领域有着非常重要的作用。
在现实世界中，角点对应物体的拐角，道路的十字路口等。从图像分析的角度来定义角点可以有以下两种定义：
- 角点可以是两个边缘的交点
- 角点是邻域内具有两个主方向的特征点
前者往往需要对图像边缘进行编码，这在很大程度上依赖于图像的分割与边缘提取，具有相当大的难度和计算量， 且一旦待检测目标局部发生变化，很可能导致操作的失败。早期主要有Rosenfeld和Freeman等人的方法，后期有CSS等方法。 基于图像灰度的方法通过计算点的曲率及梯度来检测角点，避免了第一类方法存在的缺陷， 此类方法主要有Moravec算子、Forstner算子、Harris算子、SUSAN算子等。
三、Moravec角点检测算子
在上面特征检测部分其实已经是Moravec算子的核心思想了，只是这里用数学语言重新描述一下。 在图像上取一个w×w的滑动窗口(如3×3)，不断移动这个窗口， 依次计算在8个方向上的灰度变化V(上、下、左、右以及四个对角)。 V会有三种情况：
- 如果窗口中的图像是平坦的，那么灰度变化不大
- 如果窗口中的图像是边缘，那么在沿边缘时变化不大，在垂直于边缘时变化较大
- 如果窗口中的图像是角点，那么沿任何方向，灰度变化都很大
而V可以用以下公式表示：
\[V(x,y)=\sum_{u,v}^{ }\left ( I_{x+u,y+v}-I_{x,y} \right )^{2}\]其中(u,v)是窗口相对于中心像素的偏移量，如下图所示。
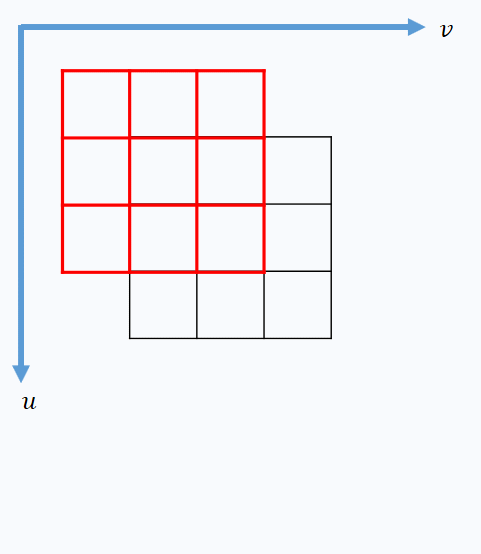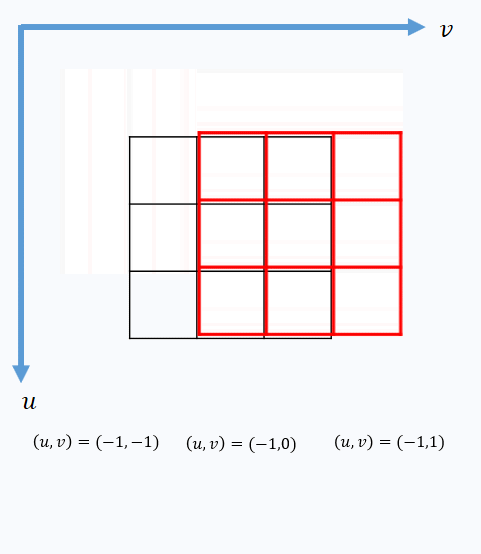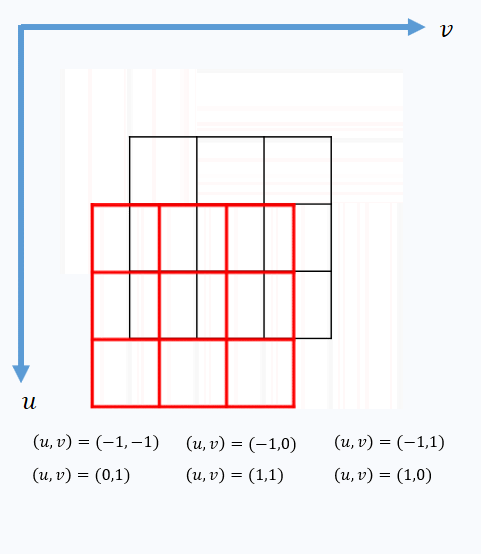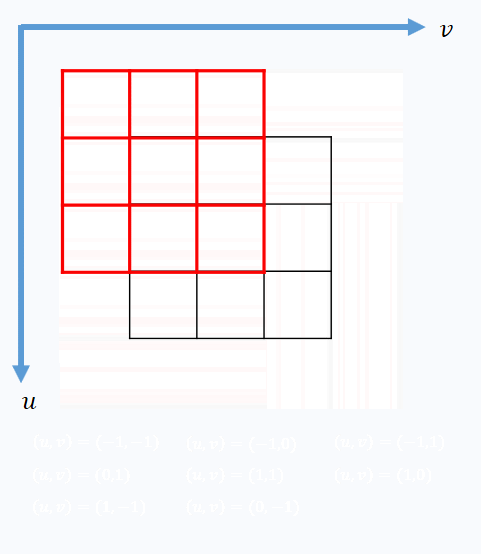由上式公式可知，V的大小可以反映在某点的灰度变化情况。因此逐像素遍历图像，
计算得到每个像素的V，然后通过对V设置合适的阈值，就可以得到检测出的角点。
但是Moravec算子也有局限性，如没有考虑于窗口中不同位置像素的权重等。因此基于它有很多改进算子。
四、Harris角点检测算子
1.Harris算子原理推导
Harris角点检测算子其实是基于Moravec算子的改进，弥补了Moravec算子的不足，主要思想类似。 首先，将窗口平移(u,v)产生灰度变化的自相关函数如下：
\[E(u,v)=\sum_{x,y}^{ }w(x,y)\left [ I(x+u,y+v)-I(x,y)\right ]^{2}\]其中w(x,y)为窗口函数，可以是平坦的，也可以是高斯函数。如下图所示：
对于等式的右边部分进行泰勒展开如下。右边是一个二元多项式，有对应的展开公式，可以不用管具体展开步骤。
其中Ix、Iy是图像I关于x、y方向的偏导。带入第一个等式，I(x,y)被消去，有：
\[E(u,v)=\sum_{x,y}^{ }w(x,y)\left [ I_{x}u+I_{y}v+O(u^{2},v^{2})\right ]^{2}\]由于u、v是对于局部的微小移动量，所以可以忽略二次余项，近似得到如下二项式函数：
\[E(u,v)\approx \sum_{x,y}^{ }w(x,y)\left ( I_{x}u+I_{y}v\right )^{2}\]然后对于等式右边平方部分，写成矩阵形式，如下：
\[(I_{x}u+I_{y}v)^{2} \\=u^{2}I_{x}^{2}+v^{2}I_{y}^{2}+2uvI_{x}I_{y} \\=\begin{bmatrix} u & v \end{bmatrix}\begin{bmatrix} I_{x}^{2} & I_{x}I_{y}\\ I_{y}I_{x} & I_{y}^{2} \end{bmatrix}\begin{bmatrix} u\\ v \end{bmatrix}\]带入上式，并令：
\[M=\sum_{x,y}^{ }w(x,y)\begin{bmatrix} I_{x}^{2} & I_{x}I_{y}\\ I_{y}I_{x} & I_{y}^{2} \end{bmatrix}\]所以有：
\[E(u,v)=\begin{bmatrix} u & v \end{bmatrix}M\begin{bmatrix} u\\ v \end{bmatrix}\]上面在忽略了余项之后，我们得到了一个二项式函数，二项式函数的本质是一个椭圆函数， 椭圆的扁率和尺寸是由M(x,y)的特征值λ1、λ2决定的，椭圆的方向是由M(x,y)的特征矢量决定的。椭圆方程如下：
\[\begin{bmatrix} u & v \end{bmatrix}M\begin{bmatrix} u\\ v \end{bmatrix}=1\]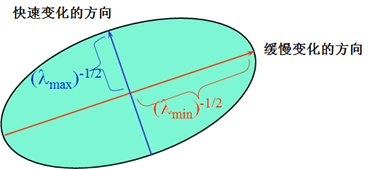
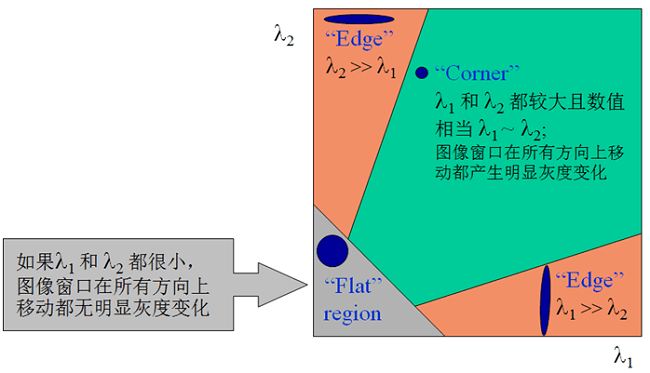
椭圆函数特征值是由M决定，而M又是由图像不同位置的偏导数决定。特征值与图像中角点、边缘、平面之间的关系可分为三种情况：
- 图像中的直线:一个特征值大，另一个特征值小，λ1>λ2或λ2>λ1。自相关函数值在某一方向上大，在其它方向上小。
- 图像中的平面:两个特征值都小，且近似相等，自相关函数数值在各个方向上都小。
- 图像中的角点:两个特征值都大，且近似相等，自相关函数在所有方向都增大。
定义判断角点函数R，如下：
\[R=det(M)-k(trace(M))^{2}\]其中：
\[trace(M) = \lambda _{1}+\lambda _{2}\] \[det(M) = \lambda _{1}\lambda _{2}\]k为经验常数，一般取值为0.04 - 0.06。 增大k的值，将减小角点响应值R，降低角点检测的灵敏性，减少被检测角点的数量； 减小k值，将增大角点响应值R，增加角点检测的灵敏性，增加被检测角点的数量。
所以上图可以用R表示成如下形式：
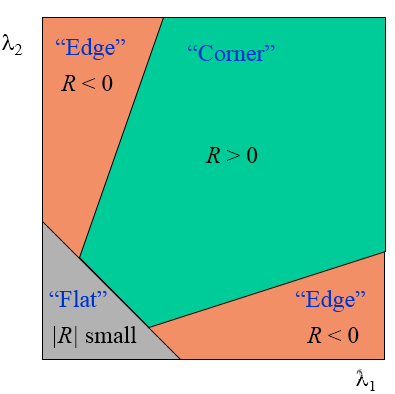其中R只与M的特征值有关。R值较大且为正数时，为角点。R值较大且为负数时，为边缘。R值较小时，为平坦区域。
在判断角点时，对角点响应函数R进行阈值处理，提取局部极大值，当R大于阈值时，认为是角点。
2.Harris算子的性质
(1)Harris角点检测算子对亮度和对比度的变化不敏感
这是因为在进行Harris角点检测时，使用了微分算子对图像进行微分运算，
而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。
换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是，
由于阈值的选择，可能会影响角点检测的数量。
所以从这个性质也可以得出一个结论，通过修改图像的亮度或对比度来大幅提升Harris算子角点的质量和数量是行不通的。
这对于Harris算子影响很小。并不是说对比度高一些Harris算子就会检测的角点多一些。
对比度增加只是对于人眼而言有感官上的视觉提升而已。
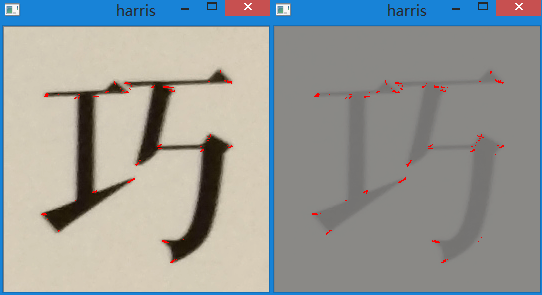
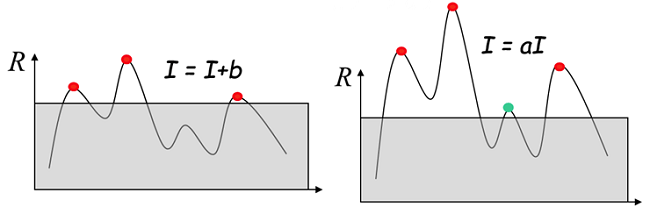下图是将同一幅图片对比度调整后Harris算子提取角点的结果，可以发现结果没有明显变化。
(2)Harris角点检测算子具有旋转不变性
Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。 而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。 当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值R也不发生变化，由此说明Harris角点检测算子具有旋转不变性。
(3)Harris角点检测算子不具有尺度不变性
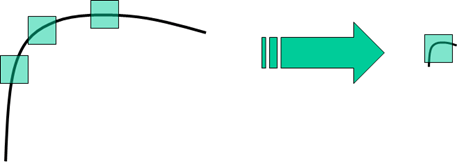
如下图所示，当右图被缩小时，在检测窗口尺寸不变的前提下，在窗口内所包含图像的内容是完全不同的。
左侧的图像可能被检测为边缘或曲线，而右侧的图像则可能被检测为一个角点。
3.OpenCV实现
在Harris算子的计算公式中，Ix、Iy可用cv2.Sobel()函数获得。在OpenCV中用函数cv2.cornerHarris()获得角点。
检测的结果是一个由角点得分(R)构成的灰度图像，得分越高表示该点是角点的可能性越大。选取合适的阈值对结果进行二值化即可得到图像中的角点。
这类似于模板匹配和直方图反向投影的返回结果。都是返回一个得分，然后设置阈值进行筛选。
(1)简单例子
# coding=utf-8
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread("E:\\harris04.jpg")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 由于Harris算子需要float32的输入图像，因此转换一下数据格式
gray = np.float32(gray)
# Harris算子
# 第一个参数是输入图像，数据类型为float32
# 第二个参数是角点检测中要考虑的领域大小
# 第三个参数是Sobel求导(Ix、Iy)时使用的窗口大小
# 第四个参数是Harris角点检测方程中的自由参数，0.04 - 0.06
dst = cv2.cornerHarris(gray, 2, 3, 0.04)
# 直接在原图上修改，也可以重新复制一份
# 0.01是人为设定的阈值
img[dst > 0.01 * dst.max()] = [0, 0, 255]
plt.imshow(dst, cmap='gray')
cv2.imshow("harris", img)
plt.show()
cv2.waitKey(0)
效果如下：
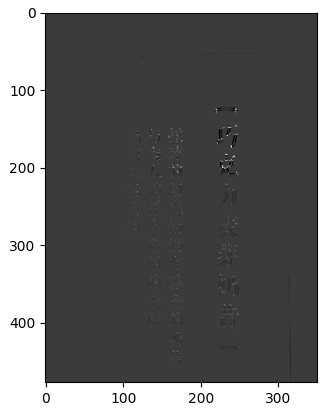第一幅图是用红色点在原图标示出的结果。第二幅图是根据计算出的R值绘制的灰度图。
我们可以利用Matplotlib放大这个灰度图，来观察R值到底有多大，是如何变化的。
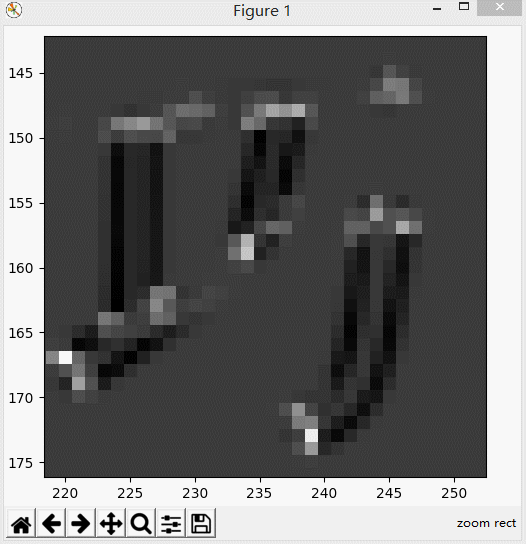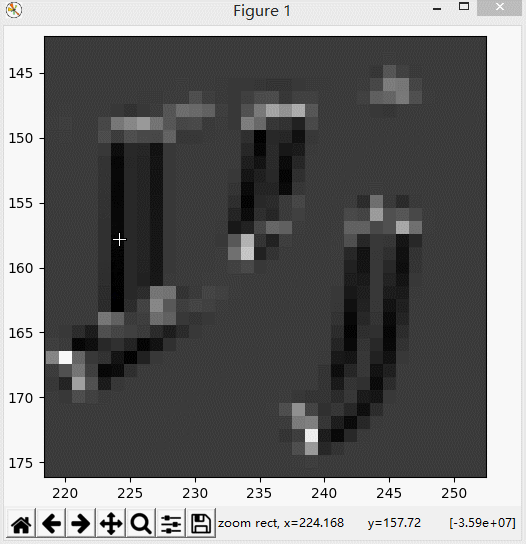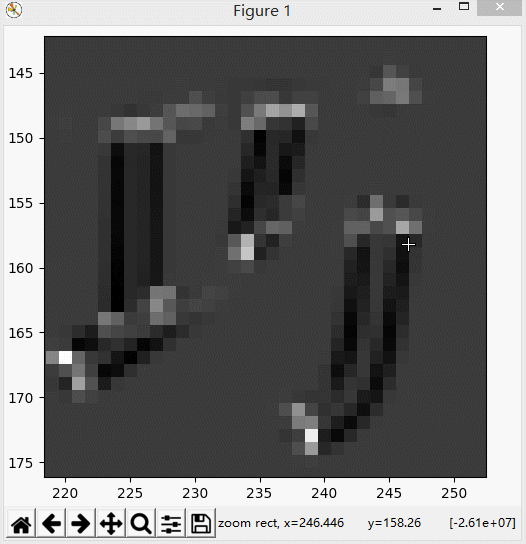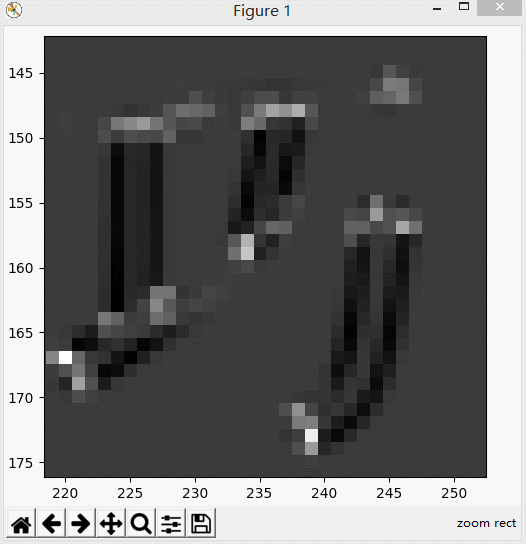可以看到边缘部分是很大的负数，大约在10的-7次方量级，
角点部分是很大的正数，大约在10的7次方量级。其它区域基本接近于0。
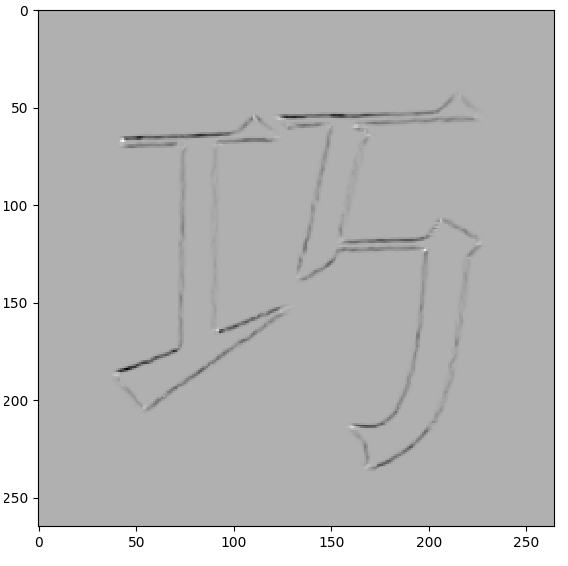
下面是对单独一个字进行Harris角点检测的对比图。
可以看到把文字的角点较好地检测出来了。下面是R值灰度图，可以较清晰地看到，角点是白色，边缘是黑色，其余部分是灰色。
(2)复杂例子
上面提取的Harris角点是像素级的，但有时我们想获取到亚像素级的角点。例如高分影像分辨率为2m。
那么一个像素就代表地面两米的距离，如果提取的Harris角点差一个像素，对应地面就是2m的误差。
在OpenCV中提供了cv2.cornerSubPix()函数。流程是首先找到Harris角点，然后将角点的重心传递给这个函数进行修正。
同时要定义一个迭代停止条件，当迭代次数达到或精度满足条件后停止。
# coding=utf-8
import cv2
import numpy as np
img = cv2.imread("E:\\harris05.png")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
gray = np.float32(gray)
dst = cv2.cornerHarris(gray, 2, 3, 0.04)
ret, dst = cv2.threshold(dst, 0.01 * dst.max(), 255, cv2.THRESH_BINARY)
dst = np.uint8(dst)
# 找到重心
ret, labels, stats, centroids = cv2.connectedComponentsWithStats(dst)
# 定义结束条件
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 100, 0.001)
# 返回值是由角点坐标组成的数组而非图像
corners = cv2.cornerSubPix(gray, np.float32(centroids), (5, 5), (-1, -1), criteria)
# 将精细化前后的坐标放在一起
res = np.hstack((centroids, corners))
# np.int0用于省略小数点后的数字(截取)
# 由于绘制只能用int所以需要把亚像素转换成整像素
# 但是可以输出float类型的corner坐标，这是精确的
res = np.int0(res)
# 绘制角点，红色代表Harris角点，绿色代表修正后角点
img[res[:, 1], res[:, 0]] = [0, 0, 255]
img[res[:, 3], res[:, 2]] = [0, 255, 0]
# 输出精确坐标
print corners
cv2.imshow("harris", img)
cv2.waitKey(0)
效果如下：
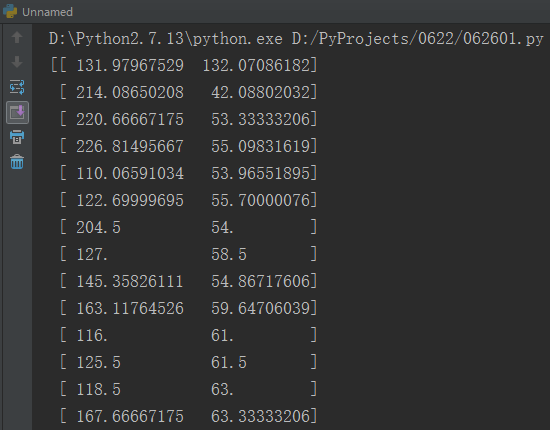红色代表Harris角点，绿色代表修正过的Harris角点坐标。但由于绘图只能使用整像素，因此对结果进行了取整，显示会有一定误差。
在控制台中输出了float类型的精确亚像素坐标，可以用于后续操作。
五、总结
本篇博客主要学习了与Harris算子有关的算法原理以及在OpenCV下的实现步骤。 Harris算子有其优势，如对图像灰度变化不敏感等，但也有一定的局限性，如不具有尺度不变性等。 后续继续学习其它算子会解决这些不足。
本文作者原创,未经许可不得转载,谢谢配合
