一、Shi-Tomasi角点检测算子
1.原理
Shi-Tomasi角点检测算子的原理很简单,而且主要思想与Harris算子类似。不同之处在于打分函数R。 在Harris算子中,打分函数如下:
\[R=det(M)-k(trace(M))^{2}\]但在Shi-Tomasi算子中对其进行了改进,变成了如下形式:
\[R=min(\lambda _{1},\lambda _{2})\]对得分进行阈值判断,超过阈值即认为是角点。可以画出下图。
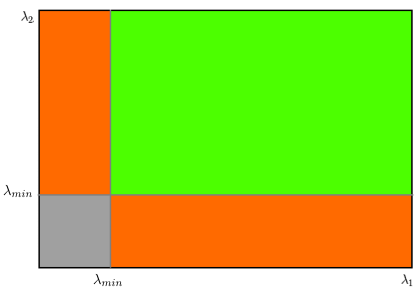 图中绿色部分是认为是角点的区域。只有当λ1和λ2都大于最小值时,才被认为是角点。
图中绿色部分是认为是角点的区域。只有当λ1和λ2都大于最小值时,才被认为是角点。
2.OpenCV实现
在OpenCV中有函数cv2.goodFeaturesToTrack()实现Shi-Tomasi算子。
这个函数可以帮我们使用Shi-Tomasi方法获取图像中N个最好的角点。
通常情况下,输入的应该是灰度图像。然后确定你想要检测到的角点数目。
再设置角点的质量水平,0到1之间。它代表了角点的最低质量,低于这个数的所有角点都会被忽略。
最后在设置两个角点之间的最短欧式距离。
根据这些信息,函数就能在图像上找到角点。所有低于质量水平的角点都会被忽略。 然后再把合格角点按角点质量进行降序排列。 函数会采用角点质量最高的那个角点(排序后的第一个), 然后将它附近(最小距离之内)的角点都删掉。按这样的方式最后返回N个最佳角点。
# coding=utf-8
import cv2
import numpy as np
img = cv2.imread("E:\\sift1.jpg")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 第一个参数是输入图像
# 第二个参数是检测的角点数目
# 第三个参数是角点质量
# 第四个参数是角点间的最短距离
corners = cv2.goodFeaturesToTrack(gray, 300, 0.01, 10)
# 将浮点型数据转成int型,否则无法绘制
corners = np.int0(corners)
for i in corners:
# 将每一项拆开,在重新拼成一个元组
x, y = i.ravel()
# 在图上绘制角点,为了更好显示,设置半径为2
cv2.circle(img, (x, y), 2, (0, 0, 255), -1)
cv2.imshow("shi-tomasi", img)
cv2.waitKey(0)
检测出的角点效果如下:
 这个算子很适合在目标跟踪中使用。
这个算子很适合在目标跟踪中使用。
二、光流法视频目标跟踪
1.光流的概念
由于目标对象或者摄像机的移动造成的图像对象在连续两帧图像中的移动被称为光流。 光流的概念是Gibson在1950年首先提出来的。 它是空间运动物体在观察成像平面上的像素运动的瞬时速度, 是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系, 从而计算出相邻帧之间物体的运动信息的一种方法。 一般而言,光流是由于场景中前景目标本身的移动、相机的运动,或者两者的共同运动所产生的。 它是一个2D向量场,可以用来显示一个点从第一帧图像到第二帧图像之间的移动。
当人的眼睛观察运动物体时,物体的景象在人眼的视网膜上形成一系列连续变化的图像,
这一系列连续变化的信息不断“流过”视网膜(即图像平面),好像一种光的“流”,故称之为光流(optical flow)。
光流表达了图像的变化,由于它包含了目标运动的信息,因此可被观察者用来确定目标的运动情况。
如下图所示。
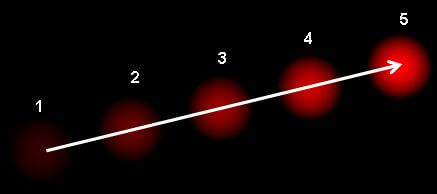 上图显示了一个点在连续的五帧图像间的移动。箭头表示光流场向量。
光流在运动重建、视频压缩、稳像等领域都有应用。
上图显示了一个点在连续的五帧图像间的移动。箭头表示光流场向量。
光流在运动重建、视频压缩、稳像等领域都有应用。
光流一般基于以下两个假设:
- 1.在连续的两帧图像之间(目标对象的)像素的灰度值不改变。
- 2.相邻的像素具有相同的运动。
2.光流方程推导
第一帧图像中的像素I(x,y,t)在时间dt后移动到第二帧图像的I(x+dx,y+dy,t+dt)处。 根据假设一,认为运动前后灰度值不变。可得到如下方程。
\[I(x,y,t)=I(x+dx,y+dy,t+dt)\]对于上式,对等式右边利用泰勒展开,消去相同项,可以得到:
\[\frac{\partial I}{\partial x}\frac{\Delta x}{\Delta t}+\frac{\partial I}{\partial y}\frac{\Delta y}{\Delta t}+\frac{\partial I}{\partial t}\frac{\Delta t}{\Delta t}=0\]而x、y对t的导数其实就是x、y方向上的速度,t对t的导数为1。
\[V_{x}=\frac{\Delta x}{\Delta t}\] \[V_{y}=\frac{\Delta y}{\Delta t}\]因此可以写成如下形式:
\[\frac{\partial I}{\partial x}V_{x}+\frac{\partial I}{\partial y}V_{y}+\frac{\partial I}{\partial t}=0\]不妨令:
\[I_{x}=\frac{\partial I}{\partial x},I_{y}=\frac{\partial I}{\partial y},I_{t}=\frac{\partial I}{\partial t}\]所以原式可以简化成:
\[I_{x}V_{x}+I_{y}V_{y}+I_{t}=0\]这个式子被称作光流方程,其中Ix和Iy是图像在x、y方向上的梯度,同样It是时间方向的梯度。 但Vx、Vy是不知道的。我们不能在一个等式中求解两个未知数。有几个方法可以帮我们解决这个问题,其中一个是Lucas-Kanade法。
3.Lucas-Kanade方法
为了求解上述光流方程,必须要增加条件。因此利用第二个假设,即相邻像素有相同运动。 Lucas-Kanade法就是利用一个3×3邻域中的9个点具有相同运动的这一点。 这样我们就可以找到这9个点的光流方程,用它们组成一个具有两个未知数的9个等式的方程组,这是一个约束条件过多的方程组。 一个好的解决方法就是使用最小二乘拟合。推导过程如下:
由于是在3×3共9个像素中运用光流方程,令n=9,所以可以得到如下9个等式:
\[I_{x}(p_{1})V_{x}+I_{y}(p_{1})V_{y}=-I_{t}(p_{1}) \\I_{x}(p_{2})V_{x}+I_{y}(p_{2})V_{y}=-I_{t}(p_{2}) \\\vdots \\I_{x}(p_{n})V_{x}+I_{y}(p_{n})V_{y}=-I_{t}(p_{n})\]为了更加简洁,可以将其写成矩阵形式Ax=b。x即使待求向量。
\[A=\begin{bmatrix} I_{x}(p_{1}) & I_{y}(p_{1})\\ I_{x}(p_{2}) & I_{y}(p_{2})\\ \vdots & \vdots\\ I_{x}(p_{n}) & I_{y}(p_{n}) \end{bmatrix} , x=\begin{bmatrix} V_{x}\\ V_{y} \end{bmatrix} ,b=\begin{bmatrix} -I_{t}(p_{1})\\ -I_{t}(p_{2})\\ \vdots \\ -I_{t}(p_{n}) \end{bmatrix}\]利用矩阵操作,直接在等式右边乘以A的逆即可。但问题是A不一定是方阵,只有方阵才可以求逆。 因此需要对A乘以A的转置,变成方阵以后再求逆。求解过程如下:
\[Ax=b\\ A^{T}Ax=A^{T}b\\ x=(A^{T}A)^{-1}A^{T}b\]其中A转置乘以A如下:
\[A^{T}A=\begin{bmatrix} I_{x}(p_{1}) &I_{x}(p_{2}) & \cdots &I_{x}(p_{n}) \\ I_{y}(p_{1}) &I_{y}(p_{2}) & \cdots &I_{y}(p_{n}) \end{bmatrix}\begin{bmatrix} I_{x}(p_{1}) & I_{y}(p_{1})\\ I_{x}(p_{2}) & I_{y}(p_{2})\\ \vdots & \vdots\\ I_{x}(p_{n}) & I_{y}(p_{n}) \end{bmatrix}\\ =\begin{bmatrix} \sum_{i=1}^{n}I_{x}(p_{i}) & \sum_{i=1}^{n}I_{x}(p_{i})I_{y}(p_{i})\\ \sum_{i=1}^{n}I_{y}(p_{i})I_{x}(p_{i}) & \sum_{i=1}^{n}I_{y}(p_{i}) \end{bmatrix}\]A转置乘以b如下:
\[A^{T}b=\begin{bmatrix} I_{x}(p_{1}) &I_{x}(p_{2}) & \cdots &I_{x}(p_{n}) \\ I_{y}(p_{1}) &I_{y}(p_{2}) & \cdots &I_{y}(p_{n}) \end{bmatrix}\begin{bmatrix} -I_{t}(p_{1})\\ -I_{t}(p_{2})\\ \vdots \\ -I_{t}(p_{n}) \end{bmatrix}\\ =\begin{bmatrix} -\sum_{i=1}^{n}I_{x}(p_{i})I_{t}(p_{i})\\ -\sum_{i=1}^{n}I_{y}(p_{i})I_{t}(p_{i}) \end{bmatrix}\]因此,最终求解结果可写成如下矩阵形式:
\[x=\begin{bmatrix} V_{x}\\ V_{y} \end{bmatrix}\\ =\begin{bmatrix} \sum_{i=1}^{n}I_{x}(p_{i}) & \sum_{i=1}^{n}I_{x}(p_{i})I_{y}(p_{i})\\ \sum_{i=1}^{n}I_{y}(p_{i})I_{x}(p_{i}) & \sum_{i=1}^{n}I_{y}(p_{i}) \end{bmatrix}^{-1}\begin{bmatrix} -\sum_{i=1}^{n}I_{x}(p_{i})I_{t}(p_{i})\\ -\sum_{i=1}^{n}I_{y}(p_{i})I_{t}(p_{i}) \end{bmatrix}\]上边的逆矩阵与Harris角点检测器非常相似,这说明角点很适合被用来做跟踪。 从使用者的角度来看,想法很简单,我们取跟踪一些点,然后我们就会获得这些点的光流向量。 但是还有一些问题。直到现在我们处理的都是很小的运动。如果有大的运动怎么办呢?答案是图像金字塔。 我们可以使用图像金字塔的顶层,此时小的运动被移除,大的运动装换成了小的运动,现在再使用Lucas-Kanade算法,我们就会得到尺度空间上的光流。
4.OpenCV中的Lucas-Kanade实现
在OpenCV中,提供了cv2.calcOpticalFlowPyrLK()以供调用,上述所有过程都被打包到了这个函数中。
我们使用函数cv2.goodFeatureToTrack()来确定视频中要跟踪的点。
首先在视频的第一帧图像中检测一些Shi-Tomasi角点,然后我们使用Lucas-Kanade算法迭代跟踪这些角点。
我们要给函数cv2.calcOpticlaFlowPyrLK()传入前一帧图像和其中的点,以及下一帧图像。
函数将返回带有状态数的点,如果状态数是1,那说明在下一帧图像中找到了这个点(上一帧中角点),
如果状态数是0,就说明没有在下一帧图像中找到这个点。我们再把这些点作为参数传给函数,如此迭代下去实现跟踪。
代码如下:
# coding=utf-8
import numpy as np
import cv2
cap = cv2.VideoCapture("E:\\v1.mp4")
# Shi-Tomasi角点检测相关参数
feature_params = dict(maxCorners=10,
qualityLevel=0.1,
minDistance=1,
blockSize=9)
# LK光流法相关参数
lk_params = dict(winSize=(30, 30),
maxLevel=2,
criteria=(cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 0.03))
# 创建随机颜色
color = np.random.randint(0, 255, (100, 3))
# 获取视频第一帧
ret, old_frame = cap.read()
# 转换为灰度
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)
# ST检测角点,注意这里参数传递的方法
p0 = cv2.goodFeaturesToTrack(old_gray, mask=None, **feature_params)
# 创建一个新的图片用于绘制
mask = np.zeros_like(old_frame)
while 1:
ret, frame = cap.read()
if frame is None:
cv2.waitKey(0)
break
else:
frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
# 计算光流
p1, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)
# 选择好的特征点
if p1 is None:
pass
elif p0 is None:
pass
else:
good_new = p1[st == 1]
good_old = p0[st == 1]
# 输出每一帧内特征点的坐标
# 坐标个数为之前指定的个数
print good_new
# 绘制轨迹
for i, (new, old) in enumerate(zip(good_new, good_old)):
a, b = new.ravel()
c, d = old.ravel()
mask = cv2.line(mask, (a, b), (c, d), color[i].tolist(), 2)
frame = cv2.circle(frame, (a, b), 5, color[i].tolist(), -1)
img = cv2.add(frame, mask)
cv2.imshow('frame', img)
k = cv2.waitKey(30) & 0xff
if k == 27:
break
# 更新上一帧以及特征点
old_gray = frame_gray.copy()
p0 = good_new.reshape(-1, 1, 2)
cv2.destroyAllWindows()
cap.release()
实现的效果如下,图中指定检测1个特征点。
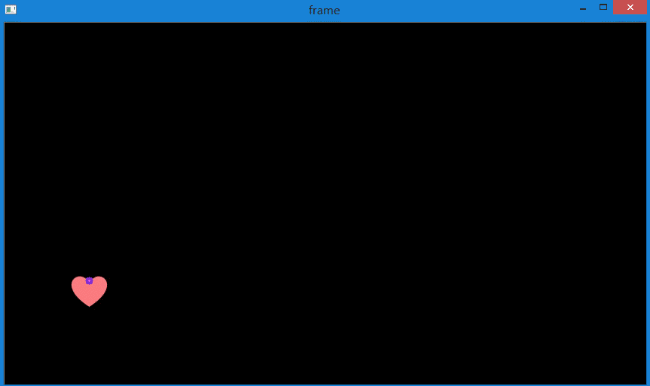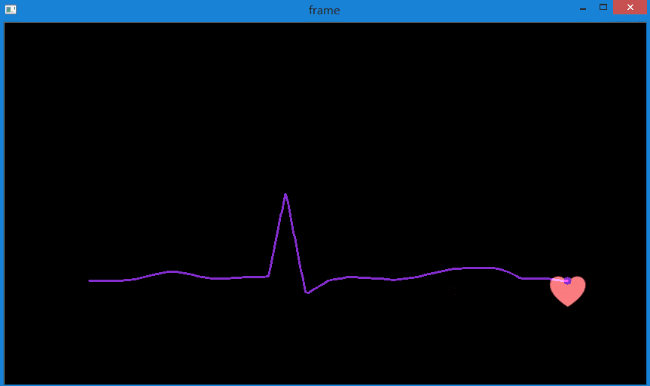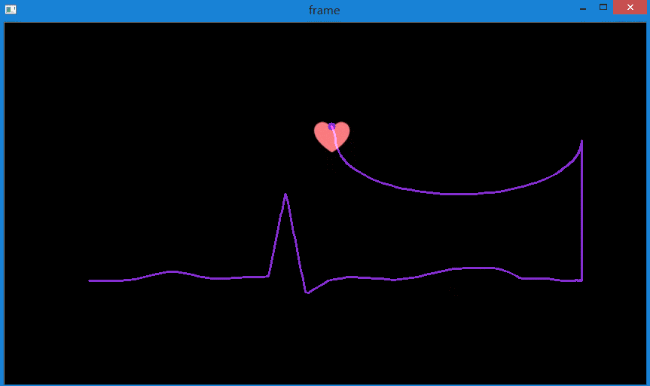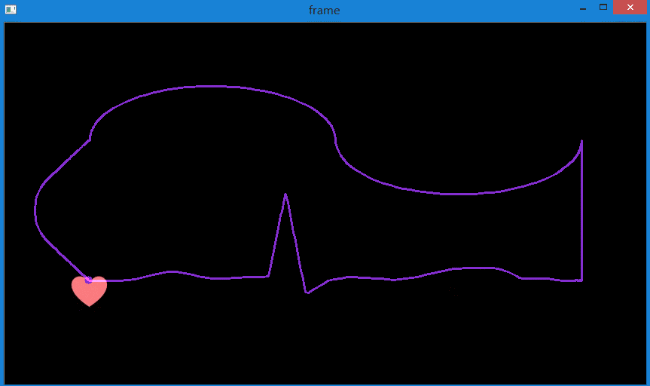 同时在控制台中输出每次追踪的轨迹坐标。
同时在控制台中输出每次追踪的轨迹坐标。
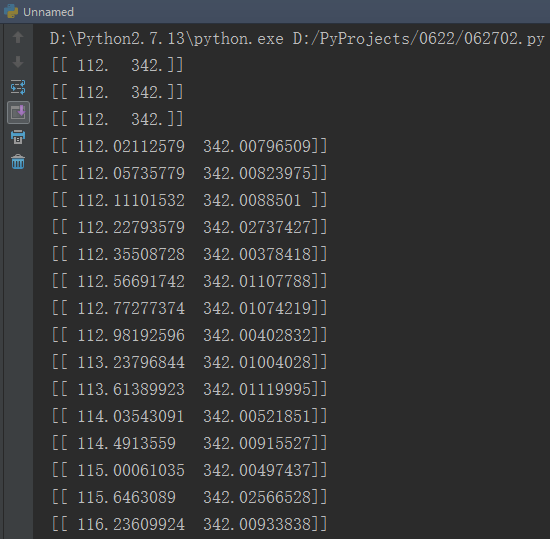 可以看到,较好地提取出了很粉色心的运动轨迹,而且得到了轨迹坐标。可用于后续处理。
下图是指定检测2个特征点。
可以看到,较好地提取出了很粉色心的运动轨迹,而且得到了轨迹坐标。可用于后续处理。
下图是指定检测2个特征点。
 同时在控制台中输出坐标。
同时在控制台中输出坐标。
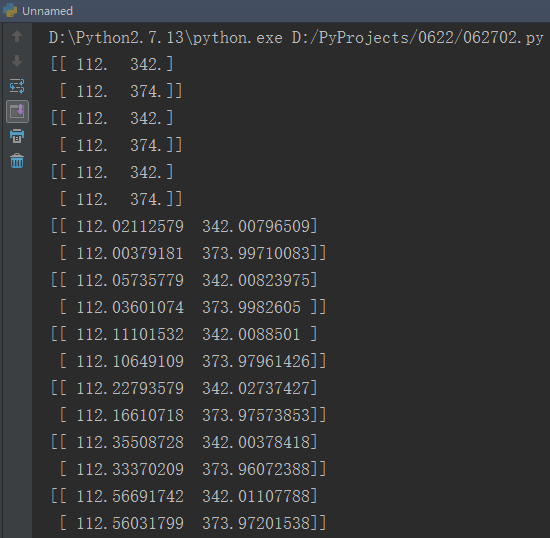 可以看到每一次输出两个坐标,因为我们指定了两个特征点。
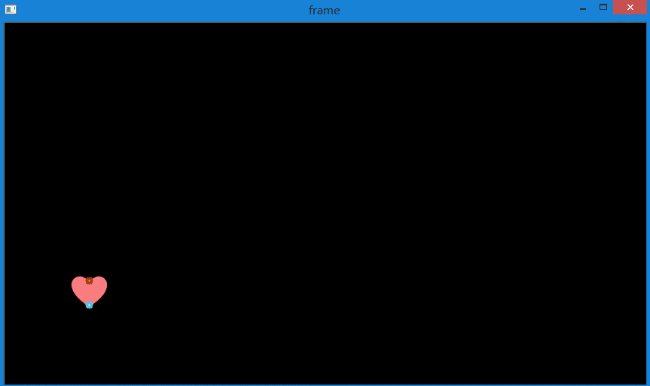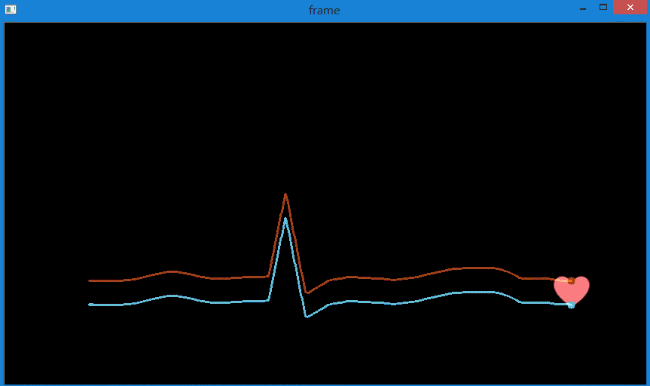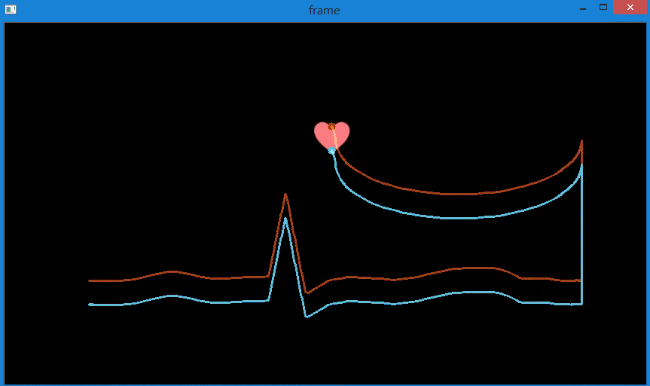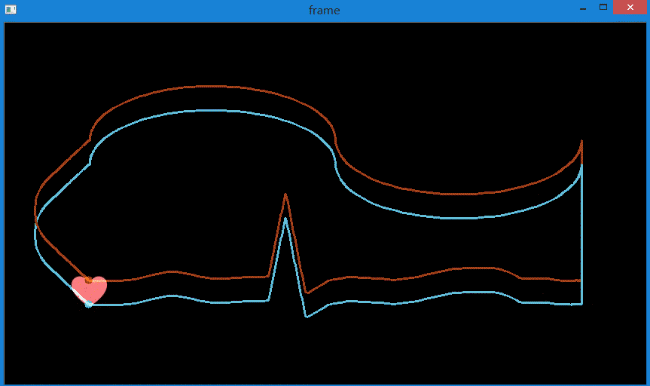
下图是检测10个特征点。
可以看到每一次输出两个坐标,因为我们指定了两个特征点。
下图是检测10个特征点。
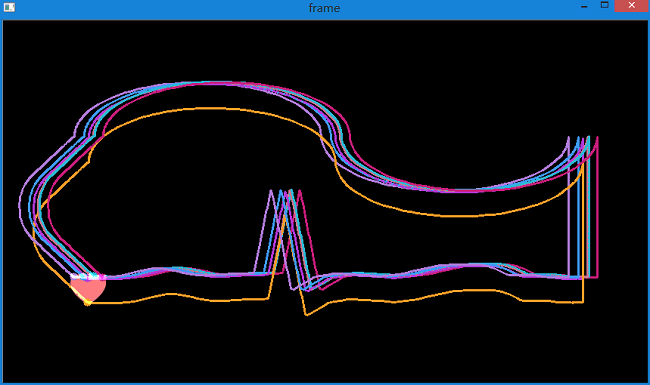 但并不是没有问题,如下图。
但并不是没有问题,如下图。
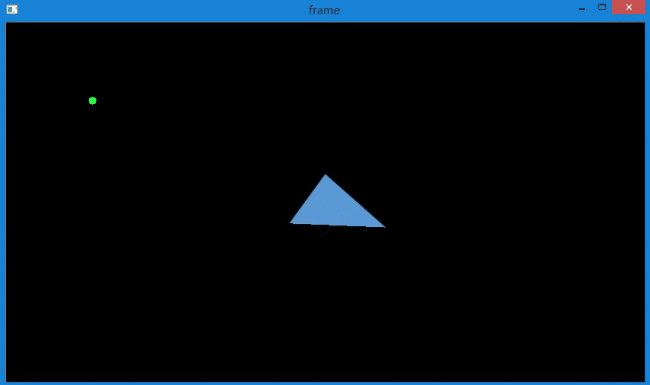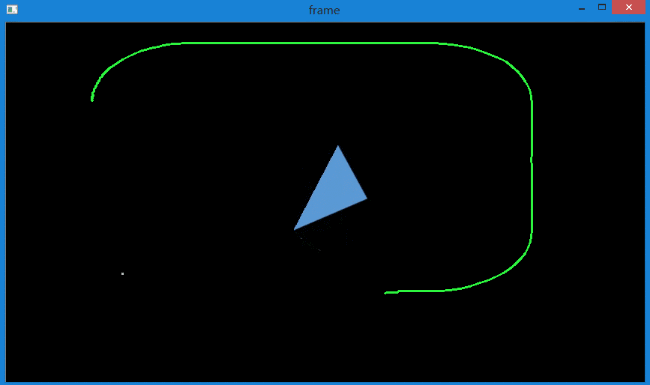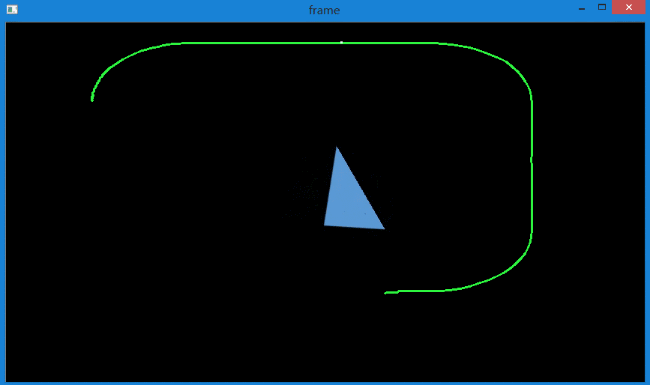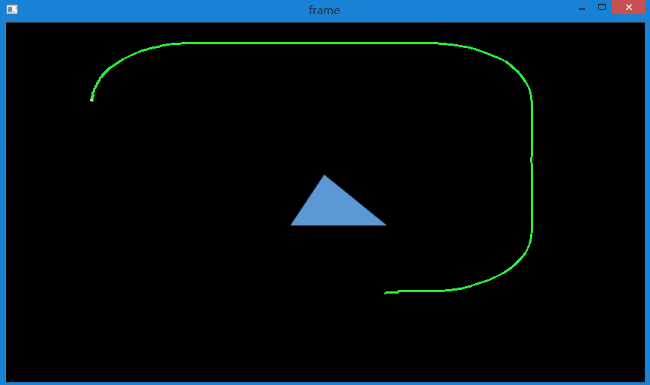 对于运动速度比较快的小目标追踪时,有可能出现追着追着就丢了的情况。
这种情况产生的原因在于,首先由于运动速度很快,所以帧间的运动范围就会很大。
而由之前的学习可知,光流法只能追踪小范围内的运动。要想追踪大范围内的运动,就需要建金字塔,然后在金字塔较高层进行追踪。
但这会带来一个问题,由于物体本身很小,经过多次降采样,在金字塔高层很有可能就找不到了。这样就无法进行追踪了。
这也就是为什么物体在加速过程中跟丢的原因。
对于运动速度比较快的小目标追踪时,有可能出现追着追着就丢了的情况。
这种情况产生的原因在于,首先由于运动速度很快,所以帧间的运动范围就会很大。
而由之前的学习可知,光流法只能追踪小范围内的运动。要想追踪大范围内的运动,就需要建金字塔,然后在金字塔较高层进行追踪。
但这会带来一个问题,由于物体本身很小,经过多次降采样,在金字塔高层很有可能就找不到了。这样就无法进行追踪了。
这也就是为什么物体在加速过程中跟丢的原因。
当增加特征点后,会发现对于旋转目标的追踪效果也不是很好,而且出现了轨迹偏移的情况,如下所示。
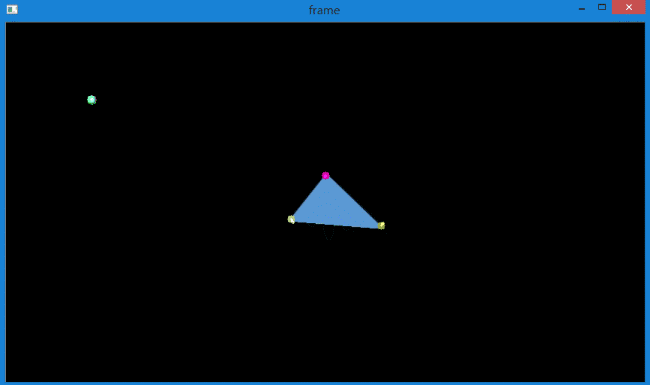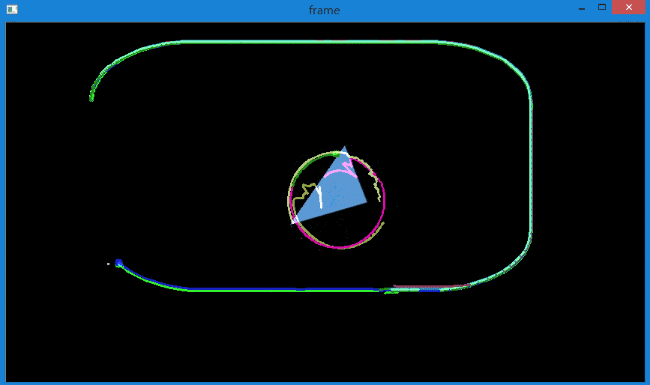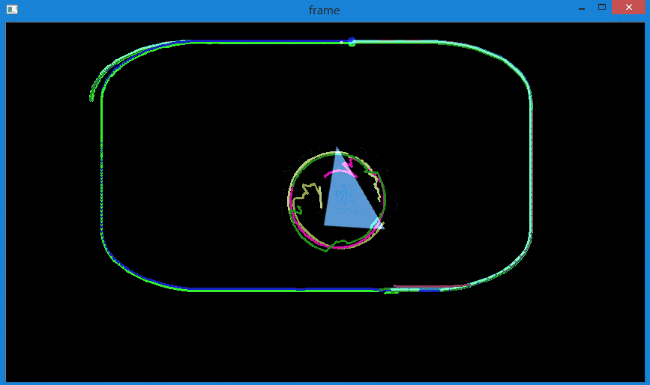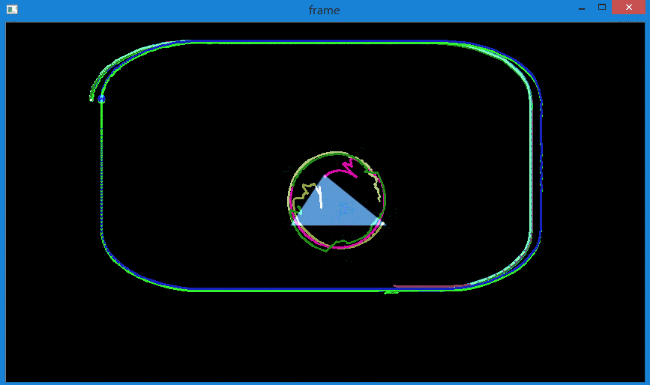 产生这种情况的原因在于,上面的代码没有对返回角点的正确性进行检查。
图像中的一些特征点甚至在丢失以后,光流还会找到一个预期相似的点。
所以为了实现稳定的跟踪,应该每个一定间隔就要进行一次角点检测,如每5帧进行一个特征点检测。
如果有必要还可以对光流点使用反向检测来选取好的点进行跟踪。
产生这种情况的原因在于,上面的代码没有对返回角点的正确性进行检查。
图像中的一些特征点甚至在丢失以后,光流还会找到一个预期相似的点。
所以为了实现稳定的跟踪,应该每个一定间隔就要进行一次角点检测,如每5帧进行一个特征点检测。
如果有必要还可以对光流点使用反向检测来选取好的点进行跟踪。
5.稠密光流
在上面的例子中,Lucas-Kanade法只是对某些指定的特征点进行了光流计算。
这种计算有一定的局限性,例如我们无法指定计算某个角点的光流,而只能指定角点个数。
OpenCV还提供了一种计算稠密光流的方法,cv2.calcOpticalFlowFarneback()。它会图像中的所有点的光流。它是基于Gunner Farneback算法。
由于是对每个像素点计算光流,所以基本达不到实时效果。函数原型如下:
calcOpticalFlowFarneback(prevImg, nextImg, flow, pyr_scale, levels, winsize, iterations, poly_n, poly_sigma, flags[, flow])
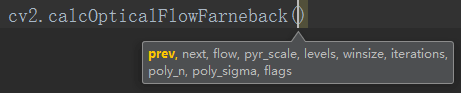
参数含义如下:
- prevImg:输入的8bit单通道前一帧图像;
- nextImg:输入的8bit单通道当前帧图像;
- flow:光流计算结果会保存在这个参数指定的变量中,可以设置为None,然后用赋值方式赋给其它变量;
- pyr_scale:金字塔参数(<1),0.5为经典参数,表示每一层是下一层尺度的一半;
- levels:金字塔的层数;
- winsize:窗口大小;
- iterations:迭代次数;
- poly_n:像素邻域的大小,一般为5或7,大的话表示图像整体比较平滑。size of the pixel neighborhood used to find polynomial expansion in each pixel;typically poly_n =5 or 7.
- poly_sigma:高斯标准差。standard deviation of the Gaussian that is used to smooth derivatives used as a basis for the polynomial expansion; for poly_n=5, you can set poly_sigma=1.1, for poly_n=7, a good value would be poly_sigma=1.5.
- flags:可以为下列的组合:
cv2.OPTFLOW_USE_INITIAL_FLOW(0)和cv2.OPTFLOW_FARNEBACK_GAUSSIAN(1);0计算快,1慢但准确。
函数的返回值是每个像素点的位移。
在OpenCV中还提供了其它两种稠密光流跟踪法:
- Horn-Schunck法
cv2.calcOpticalFlowHS() - 块匹配法
cv2.calcOpticalFlowBM()
这两种方法不支持图像金字塔匹配,不能用于跟踪大幅度的运动,而Gunnar Farneback方法支持图像金字塔,可用于大幅度运动跟踪。
下面的例子就是使用上面的算法计算稠密光流。结果是一个带有光流向量(Vx, Vy)的双通道数组。 如(576, 768, 2),表示在每一帧中长宽为576,768。在数组中,第一层是Vx,第二层是Vy。 通过计算我们能得到光流的大小和方向。我们使用颜色对结果进行编码以便于更好的观察。 方向对应于H(Hue)通道,大小对应于V(Value)通道。代码如下:
# coding=utf-8
import cv2
import numpy as np
cap = cv2.VideoCapture("E:\\vtest.avi")
ret, frame1 = cap.read()
prvs = cv2.cvtColor(frame1, cv2.COLOR_BGR2GRAY)
# 注意这里新建一个矩阵的用法
# 等价于hsv = np.zeros(frame1.shape,np.uint8)
# 但这样更加简单
hsv = np.zeros_like(frame1)
# 注意这里的用法,等价于hsv[:,:,1]=255
# 目的是把HSV的S通道全部赋成255
# S表示饱和度,即让饱和度为100%
# 这里还有个问题,为什么用HSV色彩空间
# 因为我们想用不同颜色表示不同方向,不同明暗表示大小
# 因此HSV空间最适合,最方便满足这个要求
# 如果RGB空间则很难直接办到了
# HSV面向用户,RGB面向计算机
# 从用户角度而言,HSV空间更接近于我们对于色彩的理解
hsv[..., 1] = 255
while 1:
ret, frame2 = cap.read()
next = cv2.cvtColor(frame2, cv2.COLOR_BGR2GRAY)
# 使用Gunnar Farneback方法进行稠密光流计算
# 第一个参数是上一帧影像
# 第二个参数是下一帧影像
# 第三个参数是接收结果的变量,可为空
# 第四个参数是金字塔缩放参数,每层为上层大小的0.5
# 第五个参数是金字塔层数
# 第六个参数是窗口大小
# 第七个参数是迭代次数
# 第八个参数是像素领域大小
# 第九个参数是高斯标准差
# 第十个参数是flag,表示计算方式
flow = cv2.calcOpticalFlowFarneback(prvs, next, None, 0.5, 3, 15, 3, 5, 1.2, cv2.OPTFLOW_USE_INITIAL_FLOW)
# cartToPolar函数用于计算一个二维向量的大小和角度
# flow[...,0]等价于flow[:,:,0]
# 返回的mag和ang分别是二维的一层矩阵,存放对应位置的信息,如(576, 768)
mag, ang = cv2.cartToPolar(flow[..., 0], flow[..., 1])
# 将弧度转换为角度,同时OpenCV中的H范围是180(0 - 179),所以再除以2
# 完成后将结果赋给HSV的H通道,不同的角度(方向)以不同颜色表示
# 对于不同方向,产生不同色调
# hsv[...,0]等价于hsv[:,:,0]
hsv[..., 0] = ang * 180 / np.pi / 2
# 将矢量大小标准化到0-255范围。因为OpenCV中V分量对应的取值范围是256
# 对于同一H、S而言,向量的大小越大,对应颜色越亮
hsv[..., 2] = cv2.normalize(mag, None, 0, 255, cv2.NORM_MINMAX)
# 最后,将生成好的HSV图像转换为BGR颜色空间
rgb = cv2.cvtColor(hsv, cv2.COLOR_HSV2BGR)
cv2.imshow('frame2', rgb)
# 退出控制
k = cv2.waitKey(30) & 0xff
if k == 27:
break
# 按s保存当前帧以及光流图
elif k == ord('s'):
cv2.imwrite('E:\\opticalfb.png', frame2)
cv2.imwrite('E:\\opticalhsv.png', rgb)
prvs = next
cap.release()
cv2.destroyAllWindows()
截取的部分检测效果以及原图与光流图对比如下:
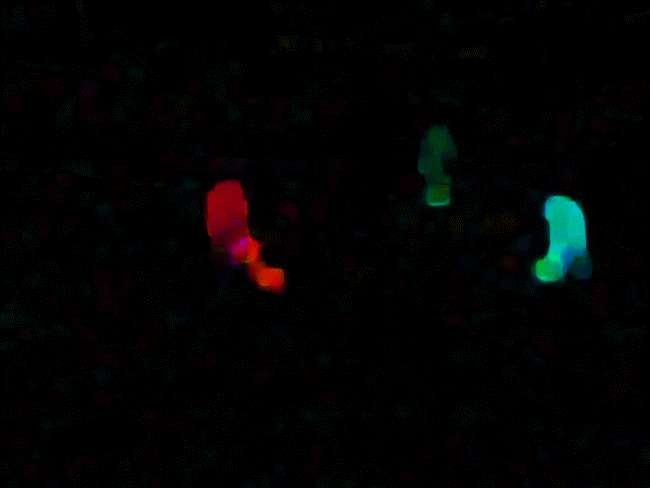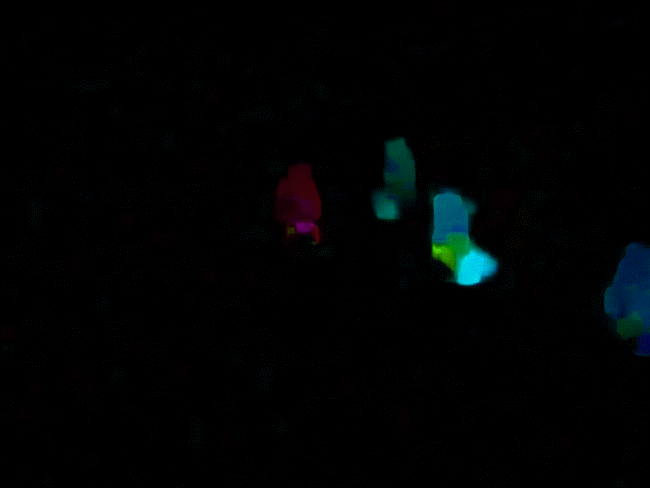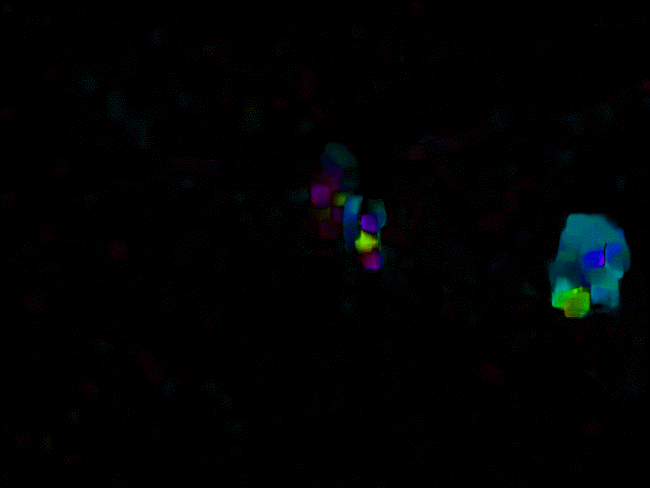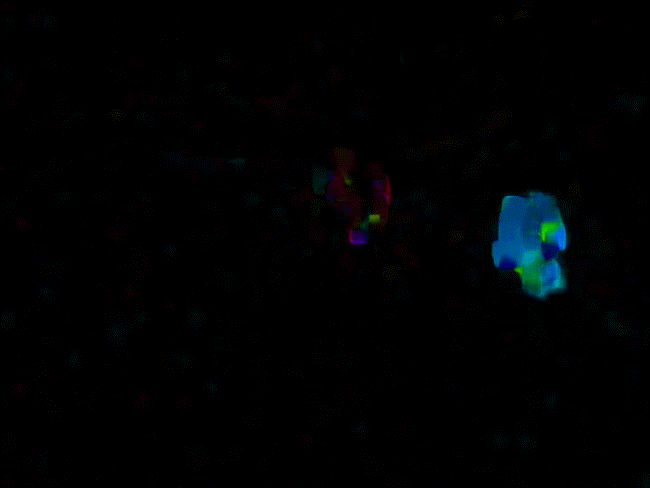
 影像中向左的运动用蓝色显示,向右运动用红色显示。同一颜色中,明暗表示运动大小。越亮表示运动越大。
可以看到采用稠密光流较好地提取出了运动物体及轨迹。
影像中向左的运动用蓝色显示,向右运动用红色显示。同一颜色中,明暗表示运动大小。越亮表示运动越大。
可以看到采用稠密光流较好地提取出了运动物体及轨迹。
三、HSV色彩空间
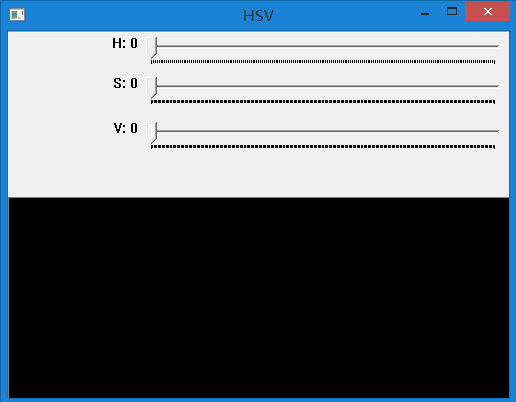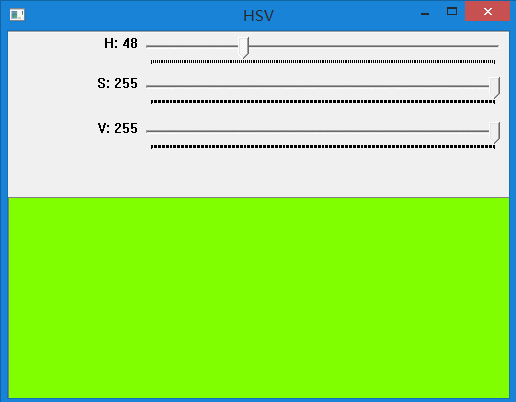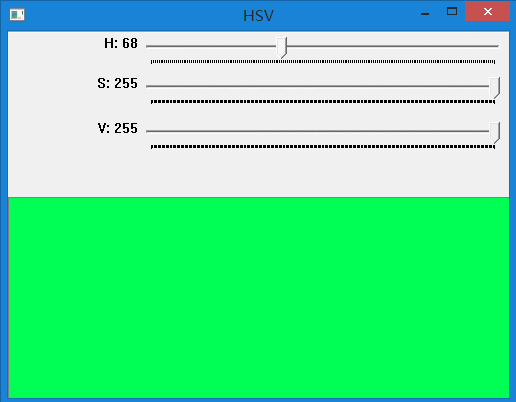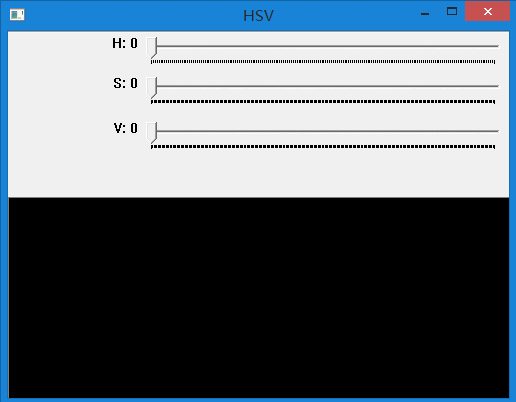
在上面代码中,通过不同颜色表示不同运动方向,不同明暗表示运动大小。 下面的代码展示了HSV颜色空间不同值对应的颜色。可对HSV空间有更直观的认识。
import cv2
import numpy as np
def nothing(x):
pass
img = np.zeros((200, 500, 3), np.uint8)
rgb = np.zeros_like(img)
cv2.namedWindow("HSV")
cv2.createTrackbar('H', 'HSV', 0, 179, nothing)
cv2.createTrackbar('S', 'HSV', 0, 255, nothing)
cv2.createTrackbar('V', 'HSV', 0, 255, nothing)
while 1:
cv2.imshow("HSV", rgb)
h = cv2.getTrackbarPos('H', 'HSV')
s = cv2.getTrackbarPos('S', 'HSV')
v = cv2.getTrackbarPos('V', 'HSV')
img[..., 0] = h
img[..., 1] = s
img[..., 2] = v
rgb = cv2.cvtColor(img, cv2.COLOR_HSV2BGR)
k = cv2.waitKey(1) & 0xff
if k == 27:
break
cv2.waitKey(0)
效果如下:
四、总结
本文主要学习了光流法视频目标运动提取的内容。围绕这个核心又介绍了Shi-Tomasi算子和HSV颜色空间。 在光流法中,介绍了稀疏光流和稠密光流两种提取方法。光流法在很多地方都有用处,也有很多内容。 以后继续学习。
本文作者原创,未经许可不得转载,谢谢配合
