好久没看TensorFlow，又看了看。还是从最基础的学起吧。虽然是最基础的东西，却也包含了运行TF的全部流程。
1.拟合平面
我们首先生成一些三维点(x、y坐标)，然后指定模型模型参数，然后根据模型算出每个点的z值。最后将这些三维点输入TF进行训练。最终TF会给我们返回估计的参数。 我们可以定义我们的模型如下：
\[y=Wx+b\]其中，x表示自变量，也就是我们这里输入的x、y坐标，y是因变量，也就是这里每个点对应的z坐标。W是x、y的系数矩阵，b是偏移量。 对应代码如下。
# coding= utf-8
import numpy as np
import tensorflow as tf
import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 参数、迭代阈值
w1 = 1.5
w2 = 0.6
b = 0.5
threshold = 0.00001
# 1.生成数据
# 这里需要强制转换成float32，否则后面在matmul时会提示float32和float64类型不匹配
# 这里的x_data包含x和y坐标
x_data = np.float32(np.random.rand(2, 100))
# 两个矩阵相乘，用的是numpy的点乘
y_data = np.dot([w1, w2], x_data) + b
# 绘制三点三维图像
ax = plt.figure().add_subplot(111, projection='3d')
ax.scatter(x_data[0, :], x_data[1, :], y_data, c='r', marker='o')
plt.show()
# 2.定义模型变量
# random_uniform用于返回一个指定大小，数值介于指定范围的矩阵
W = tf.Variable(tf.random_uniform([1, 2], -10, 10))
# 这里b的shape是(1,)，并不是1×1，第二维是任意大小，所以才能在下面和1×100的矩阵相加
b = tf.Variable(tf.zeros([1]))
y = tf.matmul(W, x_data) + b
# 3.定义评价指标
# 采用方差的定义，求取平均方差
loss = tf.reduce_mean(tf.square(y - y_data))
# 4.构造运行图
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
# 5.启动图
init = tf.global_variables_initializer()
sess = tf.Session()
# 运行之前必须要先运行这行代码，进行初始化
sess.run(init)
t1 = time.time()
count = 0
while sess.run(loss) > threshold:
sess.run(train)
count += 1
# 注意，直接打印loss并不是它的内容，必须sess.run(loss)打印出来的才是它的数值
# 因为我们在建立graph的时候，只建立tensor的结构形状信息，并没有执行数据的操作
print(count, sess.run(loss), sess.run(W), sess.run(b))
t2 = time.time()
print(t2 - t1, "seconds.")
运行代码后，绘制的三维散点图如下。
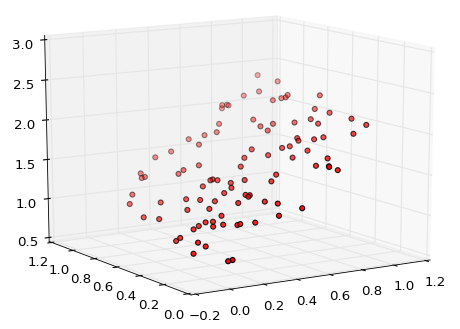控制台输出的信息如下。
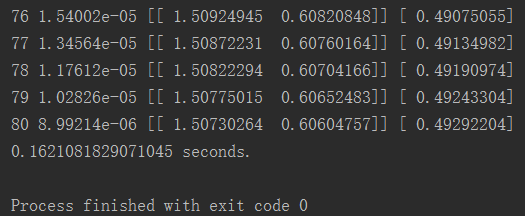可以看到，和我们最初设定的参数已经几乎一模一样了。
这样便完成了利用TF对平面进行拟合的任务。
2.拟合曲面
相比于平面，拟合曲面代码几乎不需要做什么修改。只是输入数据修改一下即可。代码如下。
# coding= utf-8
import numpy as np
import tensorflow as tf
import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 参数、迭代阈值
w1 = 2.4
w2 = 8.8
b = 0.5
threshold = 0.00001
# 1.生成数据
# 这里需要强制转换成float32，否则后面在matmul时会提示float32和float64类型不匹配
# 这里的x_data包含x和y坐标
x_coor = np.float32(np.random.rand(1, 400))
y_coor = np.float32(np.random.rand(1, 400))
x_data = np.float32(np.zeros([2, 400]))
x_data[0, :] = np.square(x_coor)
x_data[1, :] = np.square(y_coor)
y_data = np.dot([w1, w2], x_data) + b
ax = plt.figure().add_subplot(111, projection='3d')
ax.scatter(x_coor, y_coor, y_data, c='r', marker='o')
# 显示图像
plt.show()
# 2.定义模型变量
# random_uniform用于返回一个指定大小，数值介于指定范围的矩阵
W = tf.Variable(tf.random_uniform([1, 2], -10, 10))
# 这里b的shape是(1,)，并不是1×1，第二维是任意大小，所以才能在下面和1×100的矩阵相加
b = tf.Variable(tf.zeros([1]))
y = tf.matmul(W, x_data) + b
# 3.定义评价指标
# 采用方差的定义，求取平均方差
loss = tf.reduce_mean(tf.square(y - y_data))
# 4.构造运行图
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
# 5.启动图
init = tf.global_variables_initializer()
sess = tf.Session()
# 运行之前必须要先运行这行代码，进行初始化
sess.run(init)
t1 = time.time()
count = 0
while sess.run(loss) > threshold:
sess.run(train)
count += 1
# 注意，直接打印loss并不是它的内容，必须sess.run(loss)打印出来的才是它的数值
# 因为我们在建立graph的时候，只建立tensor的结构形状信息，并没有执行数据的操作
print(count, sess.run(loss), sess.run(W), sess.run(b))
t2 = time.time()
print(t2 - t1, "seconds.")
运行后，三维散点图如下。
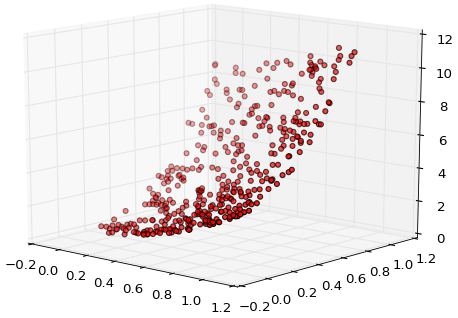控制台输出结果如下。
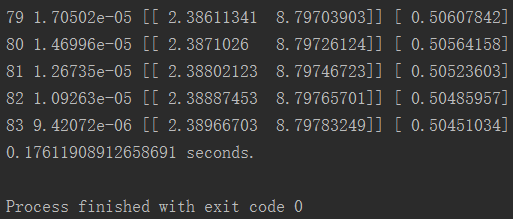
至此我们便利用TF实现了对于多项式的简单拟合。这个例子执行的流程也是后续更复杂程序的基础。
本文作者原创,未经许可不得转载,谢谢配合
