前言
在之前写了Python脚本转exe的博客,点击这里查看。
但因项目需要,需要在Linux服务器上运行Python脚本,但无奈服务器上的Python“很干净”,所有第三方的包都没有,Numpy、Matplotlib等等,但安装又很麻烦。
服务器没有联网,连基本的setuptools、pip都没有。
因此便又想到了PyInstaller。发现它不仅可以转成exe,还可以转成各种平台下对应的可执行文件。
 如在Windows下打包就变成了exe,在Linux下打包就会变成Linux下的可执行文件。
话不多说,下面直接演示效果。
如在Windows下打包就变成了exe,在Linux下打包就会变成Linux下的可执行文件。
话不多说,下面直接演示效果。
使用PyInstaller
如下是一段多项式拟合的代码:
# coding=utf-8
'''
多项式曲线拟合算法
'''
from math import *
import numpy
import random
'阶数为9阶 n=9=k'
order = 9
'被拟合的点'
xa = []
ya = []
'画图时,点的取值范围和点的密度。根据源数据点进行推断'
start = 1 # -1
end = 367 # 1
step = (start + end) / 200.0
# 实验得步长不影响图形的弯曲程度
# 此概念与KDE核密度的宽度不同
# 因为系数a0,a1,a2...已经得到,此处步长只影响画图质量,可随意设置
# 生成样例曲线上的各个点 100个
x = numpy.arange(start, end, step)
y = [((a * a - 1) ** 3 + 0.5) * sin(2 * a) for a in x]
# 生成的曲线上的各个点随机偏移一下,并放入到xa,ya中去
i = 0
##############################
# 生成xa ya的源数据点
##############################
d = []
ya = [i for i in range(start, end)]
random.shuffle(ya)
xa = range(start, end)
for i in range(len(xa)):
d.append([xa[i], ya[i]])
nd = numpy.array(d)
# 进行曲线拟合
matA = [] # 整个多项式矩阵
for i in range(0, order + 1):
matA1 = [] # 每一行
for j in range(0, order + 1):
tx = 0.0 # 每一列
for k in range(0, len(xa)):
dx = 1.0 # 表示初始
for l in range(0, j + i):
# l为次数,对应一行的不同次的变量
# 本区域(重复)运行次数越多次数越高
# 第一次不运行此区域 表示n=dx
# 最后一次运行 2order次 即为x^2k(或n^2次)
dx = dx * xa[k]
tx += dx
# 运行n次(len(xa)次)后,tx为sum(x[i]^2k) 或 n (dx=1运行n次)
matA1.append(tx)
matA.append(matA1)
# 转化为ndarray
matA = numpy.array(matA)
matB = []
for k in range(0, order + 1):
ty = 0.0
# 加和n个
for i in range(0, len(xa)):
dy = 1.0
# 对于从i=1->n 求 (x[i])^(k-1)
for l in range(0, k):
dy = dy * xa[i] # dy即为公式中 (x[i])^k
ty += ya[i] * dy # 先乘完再加和
matB.append(ty)
matB = numpy.array(matB)
# 多元一次 x^k为系数 a为未知数 求线性的a
matAA = numpy.linalg.solve(matA, matB)
# 得到系数矩阵
# 拟合后的曲线
# a0 + a1*x + a2*x^2 +...+ ak*x^k
xxa = numpy.arange(start, end, step)
yya = []
for i in range(0, len(xxa)):
yy = 0.0
for j in range(0, order + 1):
dy = 1.0
for k in range(0, j):
dy *= xxa[i] # x^k
# ak*x^k
dy *= matAA[j] # matAA[j]即为系数a
yy += dy
yya.append(yy)
print(matAA)
在CentOS上直接调用Python执行脚本正常运行如下。
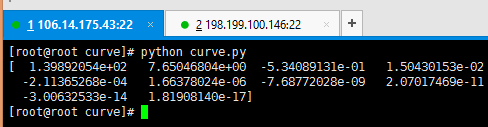 然后调用PyInstaller打包,完成后如下,与Windows下面生成的内容是类似的。
然后调用PyInstaller打包,完成后如下,与Windows下面生成的内容是类似的。
 然后直接运行生成后的可执行文件,同样可以正常运行。
然后直接运行生成后的可执行文件,同样可以正常运行。
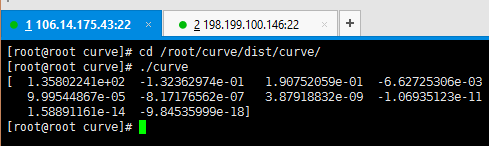 这里需要注意的是,Linux下运行可执行文件并不是cd到该目录下然后直接输入可执行文件名字就可以了。
如果这样做的话,会提示找不到命令。应该在名字前面加上”./”,表示当前目录的意思。
在DOS下执行一个文件,缺省情况下是先在当前目录下寻找,找不到的话在再PATH环境变量中寻找。
而linux下运行可执行文件的逻辑是直接只在环境变量中寻找。要执行一个可执行文件要么其在PATH路径中,这种情况可以直接写文件名;要么指明完整路径。
这里需要注意的是,Linux下运行可执行文件并不是cd到该目录下然后直接输入可执行文件名字就可以了。
如果这样做的话,会提示找不到命令。应该在名字前面加上”./”,表示当前目录的意思。
在DOS下执行一个文件,缺省情况下是先在当前目录下寻找,找不到的话在再PATH环境变量中寻找。
而linux下运行可执行文件的逻辑是直接只在环境变量中寻找。要执行一个可执行文件要么其在PATH路径中,这种情况可以直接写文件名;要么指明完整路径。
在实际测试中发现,如果使用了Anaconda环境,PyInstaller打包后的文件会比较大。上面这个脚本在Anaconda下打包有200多MB,而采用系统自带的“干净”的Python环境,打包完后是30多MB。 而且Anaconda打包后的文件有比较大可能无法运行,各种报错。因此,如果需要打包,考虑尽量避免在Anaconda环境下进行。
本文作者原创,未经许可不得转载,谢谢配合
