相机位姿估计是指给定若干图像,估计其中相机运动的问题。求解方法通常分特征点法和直接法两种,这也是视觉里程计的两类基本方法。本篇博客主要梳理和总结一下特征点法相机位姿估计。
特征点法的思路是先从图像当中提取许多特征,然后在图像间进行特征匹配,这样就得到许多匹配好的点,再根据这些点进行相机位姿的求解。 关于特征点匹配可以参考之前写的这篇博客,基于ORB进行特征提取和匹配。 相机位姿求解部分则和图像本身关系不大了。特征匹配后得到了多组配对点以及它们的像素坐标。剩下的问题是说,怎么用多组配对点去计算相机的运动。根据传感器形式的不同,可以分成三种情况:
- 2D-2D,单目相机获取的影像,只能获得像素坐标
- 3D-3D配对点,RGBD或双目相机,可以获取深度信息
- 3D-2D,已知一张图中的3D信息,另一张图只有2D信息
1.总的思路
首先做一些必要的变量定义,如下图。
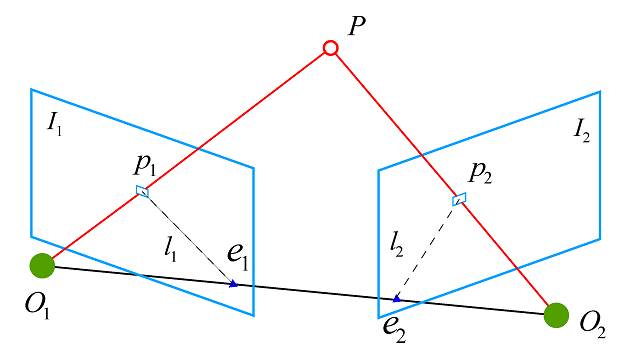
在两帧各自的相机坐标系中,设P点的相机坐标系的坐标分别为\(P_{1}\)、\(P_{2}\)。
\[P_{1}=\begin{pmatrix} X_{1}\\ Y_{1}\\ Z_{1} \end{pmatrix},P_{2}=\begin{pmatrix} X_{2}\\ Y_{2}\\ Z_{2} \end{pmatrix}\]相机从第一帧移动到第二帧,其旋转矩阵设为R,平移向量设为t。这里的R表示的旋转是相对于第一帧的姿态改变量。那么有
\[P_{2}=RP_{1}+t\]我们最终的目的就是要根据这个运动方程,求解出相机的运动,也就是R、t。这便是我们总的思路。 后续所有其实都是围绕这个公式展开的。
稍微梳理一下就会发现,\(P_{1}\)、\(P_{2}\)的坐标我们并不知道,我们已知的只是\(p_{1}\)、\(p_{2}\),也即两幅影像匹配的同名点的像素坐标。 所以我们要根据上面的式子求得R、t,就要知道\(P_{1}\)、\(P_{2}\),但现在我们只知道\(p_{1}\)、\(p_{2}\)。 因此我们需要找到\(p_{1}\)、\(p_{2}\)和\(P_{1}\)、\(P_{2}\)的关系。而这,其实就是之前说过的小孔成像模型的内容。这里再次回顾一下。
2.小孔成像模型
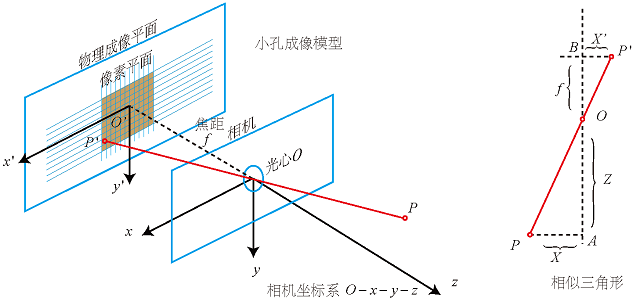
要想找到相机坐标系和像素坐标系的关系,根据前面的知识我们就是要在相机坐标系、图像坐标系和像素坐标系三个坐标系之间转换,从而找到彼此的关联。 这三个坐标系的定义在之前这篇博客中有提到。 我们用\(p_{1}\)、\(p_{2}\)表示像素坐标,用\(P_{1}^{'},P_{2}^{'}\)表示图像坐标,有
\[p_{1}=\begin{pmatrix} u_{1}\\ v_{1} \end{pmatrix},p_{2}=\begin{pmatrix} u_{2}\\ v_{2} \end{pmatrix},P_{1}^{'}=\begin{pmatrix} X_{1}^{'}\\ Y_{1}^{'}\\ Z_{1}^{'} \end{pmatrix},P_{2}^{'}=\begin{pmatrix} X_{2}^{'}\\ Y_{2}^{'}\\ Z_{2}^{'} \end{pmatrix}\]由于两张影像的小孔成像模型是相同的,这里为了简单,就只推导第一帧影像的模型了。在第一帧影像的模型中,由三角形相似可以得到如下式子
\[\frac{X_{1}}{X_{1}^{'}}=\frac{Y_{1}}{Y_{1}^{'}}=\frac{Z_{1}}{f_{1}}\]由图像坐标系的定义可知,其x’y’平面到光心的距离就是相机的焦距f,所以是常量。稍作整理可以得到
\[\left\{\begin{matrix} X_{1}^{'}=\frac{f_{1}}{Z_{1}}X_{1}\\ Y_{1}^{'}=\frac{f_{1}}{Z_{1}}Y_{1} \end{matrix}\right.\]这个式子表达了相机坐标系和图像坐标系的关系。那么接着寻找图像坐标系和像素坐标系的关系。由于这两个坐标系都在同一平面,其实只是相差了坐标原点的平移和尺度的缩放。因此可以写成如下形式
\[\left\{\begin{matrix} u_{1} = \alpha_{1} X_{1}^{'}+c_{x1}\\ v_{1} = \beta_{1} Y_{1}^{'}+c_{y1} \end{matrix}\right.\]这个式子表示了图像坐标系和像素坐标系的关系。因此要想得到相机坐标系和像素坐标系的关系,理所应当应该把上面得到的图像坐标公式带入这里,有
\[\left\{\begin{matrix} u_{1} = \alpha_{1} \frac{f_{1}}{Z_{1}}X_{1}+c_{x1}\\ v_{1} = \beta_{1} \frac{f_{1}}{Z_{1}}Y_{1}+c_{y1} \end{matrix}\right.\]这个式子便是相机坐标系和像素坐标系的关系了。这里的f是相机的焦距,也就是相机光心到相面的距离,内参之一,是一个已知常量。而α、β是两个坐标系之间的缩放倍数,一般认为也不会轻易改变。所以将它们合并为一个新的变量
\[\left\{\begin{matrix} f_{x1}=\alpha_{1} f_{1}\\ f_{y1} = \beta_{1} f_{1} \end{matrix}\right.\]因此
\[\left\{\begin{matrix} u_{1} = \frac{X_{1}}{Z_{1}}f_{x1}+c_{x1}\\ v_{1} = \frac{Y_{1}}{Z_{1}}f_{y1}+c_{y1} \end{matrix}\right.\]为了后续方便,将这个式子写成矩阵形式,这样\(p_{1}\)就要用齐次坐标表示,也就是加一个维度
\[\begin{pmatrix} u_{1}\\ v_{1}\\ 1 \end{pmatrix}=\frac{1}{Z_{1}}\begin{pmatrix} f_{x1} & 0 & c_{x1}\\ 0 & f_{y1} & c_{y1}\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X_{1}\\ Y_{1}\\ Z_{1} \end{pmatrix}\]用另一种写法表示,如下
\[p_{1}=\frac{1}{Z_{1}}K_{1}P_{1}\]稍微注意一下的是这里的\(p_{1}\)现在是齐次坐标了,和一开始定义的\(p_{1}\)不一样了。 仔细观察上式发现,它表达了相机坐标与像素坐标的关系,正是我们想要的。我们现在已知的是像素坐标\(p_{1}\)。所以我们用\(p_{1}\)表示\(P_{1}\)如下
\[P_{1}=K_{1}^{-1}Z_{1}p_{1}\]同理,
\[P_{2}=K_{2}^{-1}Z_{2}p_{2}\]3.运动方程
由小孔成像模型我们得到了用像素坐标表示的相机坐标。 将得到的\(P_{1}\)、\(P_{2}\)带入最开始的运动方程,对于同一个相机,很明显内参矩阵K短期内是相同的,\(K_{1}=K_{2}\),之后统一用K表示。 但\(Z_{1}\)很明显一般情况下不等于\(Z_{2}\),除非是相机绕着P点为圆心旋转。
\[K^{-1}Z_{2}p_{2}=RK^{-1}Z_{1}p_{1}+t\]至此便得到了一个公式,据此可以算出R,t。但会发现问题,我们已知的是K、\(p_{1}\)、\(p_{2}\),待求R,t。 然而这里还有\(Z_{1}\)、\(Z_{2}\)是未知的,因此必须想办法将Z消去。
回到之前的齐次方程那里,也就是这个式子
\[\begin{pmatrix} u_{1}\\ v_{1}\\ 1 \end{pmatrix}=\frac{1}{Z_{1}}\begin{pmatrix} f_{x1} & 0 & c_{x1}\\ 0 & f_{y1} & c_{y1}\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X_{1}\\ Y_{1}\\ Z_{1} \end{pmatrix}\]可以发现,Z是在这里出来的。写成简化形式
\[p_{1}=\frac{1}{Z_{1}}K_{1}P_{1}\]如果让方程两边都乘以\(Z_{1}\),就可以把\(1/Z_{1}\)消掉了。
\[Z_{1}p_{1}=K_{1}P_{1}\]但方程左边有多了个Z,因此两边同时再乘以\(1/Z_{1}\),那么左边的Z就没有了,并且P1的Z分量就变成了1。
\[\begin{pmatrix} u_{1}\\ v_{1}\\ 1 \end{pmatrix}=K\begin{pmatrix} X_{1}/Z_{1}\\ Y_{1}/Z_{1}\\ 1 \end{pmatrix}\]需要注意的是,这里的\(P_{1}\)的X、Y坐标再也不是以前的\(X_{1}\)、\(Y_{1}\)了,而是变成了\(X_{1}/Z_{1}\)、\(Y_{1}/Z_{1}\)。
\[P_{1}^{'}=\begin{pmatrix} X_{1}/Z_{1}\\ Y_{1}/Z_{1}\\ 1 \end{pmatrix}\]就把这个坐标叫做归一化相机坐标。所以有
\[\left\{\begin{matrix} P_{1}^{'}=K_{1}^{-1}p_{1}\\ P_{2}^{'}=K_{2}^{-1}p_{2} \end{matrix}\right.\]这样便把Z消去了,再次带入运动方程,
\[K^{-1}p_{2}=RK^{-1}p_{1}+t\]这样便能求解了。但是也导致了一个问题,因为不同帧对应的相机坐标系中P的Z值并不相等。在实际操作中分别除以其本身从而将Z分量归一化为1,这其实就丢失了真实的位置信息,不同帧的缩放是不等的!从而导致2D-2D估计两两帧之间,每次估计的尺度都是不同的。这也就是单目SLAM的尺度不确定性。
举例来说,有f1、f2、f3共3张影像。首先,f1-f2匹配获得匹配点像素坐标,直接套用上面的公式,可以获得其归一化相机坐标
\[P_{1}=Kp_{1}\]但问题是并不知道它是缩放了多少倍才变成这样的,假设缩放为Z1。同理f2-f3有公式
\[P_{2}=Kp_{2}\]假设其缩放了Z2倍。一般情况下Z1不会等于Z2。这样,我们就没有办法真正去恢复其真实的移动t。恢复的只是在统一的归一化坐标系下的移动量。
用一个示意图表示如下
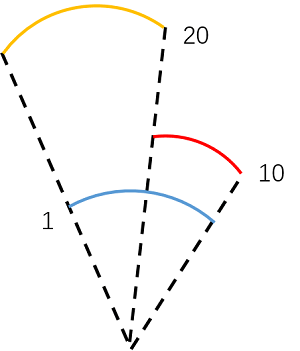
例如某帧的Z=20,另一帧的Z=10,它们各自分别缩小20、10倍变成了1。 但我们只知道它们缩放后的结果都是1,并不知道缩放的倍数。 因此后面用R,t恢复也不是真实的平移量。当然R(旋转)不会受影响。但是t的尺度是未知的,所以直接拿2D-2D估计位姿是有问题的。所以应该考虑其它办法,比如3D-2D。流程是对于第一、二帧先用2D-2D算出R、t,后续帧采用3D-2D计算,以第一次2D-2D估计出来的t作为单位长度来表示后续的t。如果能知道单位长度的真实距离,后续帧移动的真实距离也就都可以算出了。用流程图可以表示如下:

接着刚刚上面的运动方程,我们引入新的符号来表示P点归一化以后的相机坐标
\[\left\{\begin{matrix} x_{1}=P_{1}^{'}=K_{1}^{-1}p_{1}\\ x_{2}=P_{2}^{'}=K_{2}^{-1}p_{2} \end{matrix}\right.\]再次解释一下变量含义。这里\(p_{1}\)、\(p_{2}\)是齐次以后的像素坐标,K为相机内参矩阵。\(x_{1}\)、\(x_{2}\)是归一化后的相机坐标。将其重新带入运动方程,有
\[\begin{matrix} K^{-1}p_{2}=RK^{-1}p_{1}+t\\ x_{2}=Rx_{1}+t \end{matrix}\]因此下面研究的问题就是,如何由一堆对应的\(x_{1}\)、\(x_{2}\),算出R,t。在一开始说了三种情况,对于三种不同情况,有不同的方法解决。
4.分情况讨论
(1)2D-2D
a.基于本质矩阵E
还是由第一部分推得的运动方程出发。目标是求取R,t。先在方程两边叉乘t。
\[\begin{matrix} t\times x_{2}=t\times (Rx_{1}+t)\\ t\times x_{2}=t\times Rx_{1}+t\times t=t\times Rx_{1} \end{matrix}\]根据叉乘性质,一个向量叉乘它本身为0,所以就没有了。然后左右两边同时乘以\(x_{2}^{T}\),得到
\[x_{2}^{T}(t\times x_{2})=x_{2}^{T}(t\times Rx_{1})=0\]为什么左边乘个\(x_{2}\)就等于0了呢。因为方程左边t叉乘\(x_{2}\)表示的含义是一个垂直于t、\(x_{2}\)向量所组成的平面的向量。 而\(x_{2}\)在这个平面内,因此它与这个向量必然垂直,所以点乘为0。这样便得到了一个看起来十分简单的式子。
\[x_{2}^{T}t\times Rx_{1}=0\]看过前面博客的便知道,这便是“大名鼎鼎”的对极约束方程了。为了使其更好看一点,定义E=t×R。所以对极约束就写成了这样
\[x_{2}^{T}Ex_{1}=0\]前面说了,知道了像素坐标和内参矩阵,由公式就可以算出归一化相机坐标,带入对极约束就可以计算了,这也就是对极约束的“输入”。
在OpenCV中,只需要将两幅影像上匹配好的点和内参矩阵输入,即可得到E和R,t,这是因为OpenCV自动根据像素坐标和内参矩阵,求得了归一化相机坐标,然后将其带入对极约束计算。 因此自己在计算的时候不能直接拿匹配的像素坐标(u,v)来带入计算。因为很明确,公式中的\(x_{1}\)、\(x_{2}\)是归一化后的相机坐标,并不是像素坐标。
因此从公式上严格来说,对极约束的输入是内参矩阵和归一化相机坐标,对极约束描述的是相机运动前后物体在归一化相机坐标系下的关系。 只是因为OpenCV帮我们简化了,所以只需要输入内参矩阵和像素坐标,从而造成了一种对极约束的输入是像素坐标这样一种错觉。
因此,2D-2D求解位姿,便成了先找到一堆匹配点求E。然后对E进行分解,得到R,t。
求E有五点法和八点法。所谓五点法是指,t有三个自由度,R有三个自由度,所以E应该有6个自由度。又因为缩放,所以减少一个自由度,最终是5个自由度。也就至少需要5对点求解。5点法用了E的内在性质,解起来比较麻烦。因此有了8点法。8点法简而言之就是不管E的内在性质,直接把E当成普通的矩阵求解。E一共有9个未知数,去掉一个缩放因子,还剩8个。所以至少需要8对点求解。
将对极约束展开
\[\begin{pmatrix} x_{2} & y_{2} & 1 \end{pmatrix}\begin{pmatrix} E_{11} & E_{12} & E_{13}\\ E_{21} & E_{22} & E_{23}\\ E_{31} & E_{32} & E_{33} \end{pmatrix}\begin{pmatrix} x_{1}\\ y_{1}\\ 1 \end{pmatrix}=0\]通过变形可以得到下面的Ax=0形式
\[\begin{pmatrix} x_{2}x_{1} & x_{2}y_{1} & x_{2} & y_{2}x_{1} & y_{2}y_{1} & y_{2} & x_{1} & y_{1} & 1 \end{pmatrix}\begin{pmatrix} E_{11}\\ E_{12}\\ \vdots \\ E_{33} \end{pmatrix}=0\]由于匹配得到的点对个数远大于未知数个数,因此需要寻求最小二乘解。解法就是对这个系数矩阵A进行SVD分解,然后找到奇异值矩阵中最小奇异值所对应的奇异向量,即为方程的最小二乘解。相关原理在这篇博客中也介绍了。
由5点或是8点算出了E之后,下面便是对E进行分解求R,t。简单来说就是对E进行SVD分解。然后套用下面的公式进行计算。
\[R = UR_{Z}^{T}(\pm \frac{\pi}{2})V^{T},\widehat{t}=UR_{Z}(\pm \frac{\pi}{2})\Sigma U^{T}\]这里\(R_{z}\)表示绕Z轴正负旋转90度的矩阵。
\[R_{Z}(\theta )=\begin{pmatrix} cos\theta & sin\theta & 0\\ -sin\theta & cos\theta & 0\\ 0 & 0 & 1 \end{pmatrix}\] \[R_{Z}(\frac{\pi}{2})=\begin{pmatrix} 0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 1 \end{pmatrix},R_{Z}(-\frac{\pi}{2})=\begin{pmatrix} 0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1 \end{pmatrix}\]b.基于基础矩阵F
在不知道相机内参的情况下,是否也能计算R,t呢。答案是肯定的。回到运动方程,将\(x_{1}\)、\(x_{2}\)写开,如下
\[\begin{matrix} (K^{-1}p_{2})^{T}t\times R K^{-1}p_{1}=0 \end{matrix}\]由矩阵转置准则拆开整理可得
\[\begin{matrix} p_{2}^{T}(K^{-1})^{T}t\times R K^{-1}p_{1}=0 \end{matrix}\]\(p_{1}\)、\(p_{2}\)中间的这部分单独拿出来就叫做F矩阵,基础矩阵。
\[F=K^{-T}t\times R K^{-1}\]求F矩阵的方法和求E类似。利用基础矩阵同样可以求得R,t,只是分解起来要麻烦一些。 这里要注意,基础矩阵对应的公式中,输入是齐次的像素坐标,而不是归一的相机坐标,注意区分。
c.基于单应矩阵H
最后还有一种情况就是所有点都落在同一平面上,如墙、地面等。这时可以用单应矩阵描述处于同一平面上的一些点在两张图像间的变换关系。假设有某个平面P,满足平面方程
\[n^{T}P+d=0\]因为
\[P_{2}=RP_{1}+t\]所以
\[p_{2}=KP_{2}=K(RP_{1}+t)\]由平面方程可得
\[-\frac{n^{T}P}{d}=1\]带入上式让其与t相乘,经过化简,最终可得
\[p_{2}=K(R-\frac{tn^{T}}{d})K^{-1}p_{1}\]把\(p_{1}\)前面的这些单独拿出来,就是单应矩阵H。 用单应矩阵恢复位姿流程和之前一样,先求H,然后用各种手段分解H。注意这里公式的输入还是齐次的像素坐标。
至此,2D-2D的位姿估计大致就这样了。这里还有个需要注意的地方。那就是在估计位姿时,一般经验做法是会同时估计E或F和H,然后选择重投影误差比较小的那个作为最终的运动估计矩阵。
关于3D-2D、3D-3D的位姿估计,下篇博客继续吧。
5.参考资料
- https://www.zhihu.com/question/51510464
本文作者原创,未经许可不得转载,谢谢配合
