这篇博客主要综合之前讲过的相机小孔成像模型、坐标系等内容再次重新梳理一遍，并且引出相机畸变以及纠正的原理和例子。
一、常用坐标系及成像模型
在这篇博客中，简单介绍了各种坐标系，这里再重新梳理一下。 在相机的成像模型中，主要涉及以下几个坐标系：
- 世界坐标系
- 相机坐标系
- 像平面坐标系
- 像素坐标系
1.世界坐标系
所谓世界坐标系，即指真实坐标系。例如WGS84等坐标系。度量单位一般为米。
2.相机坐标系
相机坐标系顾名思义是以相机的光心为原点的坐标系，z轴为主光轴方向，一般指向相机拍摄方向。x、y方向一般规定为让z轴对着自己，水平方向为x轴，方向向右。y轴则为竖直方向，满足右手定则。度量单位一般也为米。在相机坐标系的概念下还有个比较特别的相机坐标系，即让所有坐标的Z分量都为1。这样所有点都在Z=1这个平面上，这个坐标系被称为归一化相机坐标系，在后面也会经常用到。
3.像平面坐标系
像平面坐标系则是以相机光心沿着主光轴在像面上的投影作为坐标原点，x、y轴与相机坐标系的x、y平行。度量单位一般为米。
4.像素坐标系
像素坐标系属于计算机图形中的概念了。对于一幅图像而言，其图像的左上角点为坐标原点，水平方向向右为x轴(u轴)，数值方向向下为y轴(v轴)。度量值为像素。
下面这个图反映了各坐标系之间的关系。
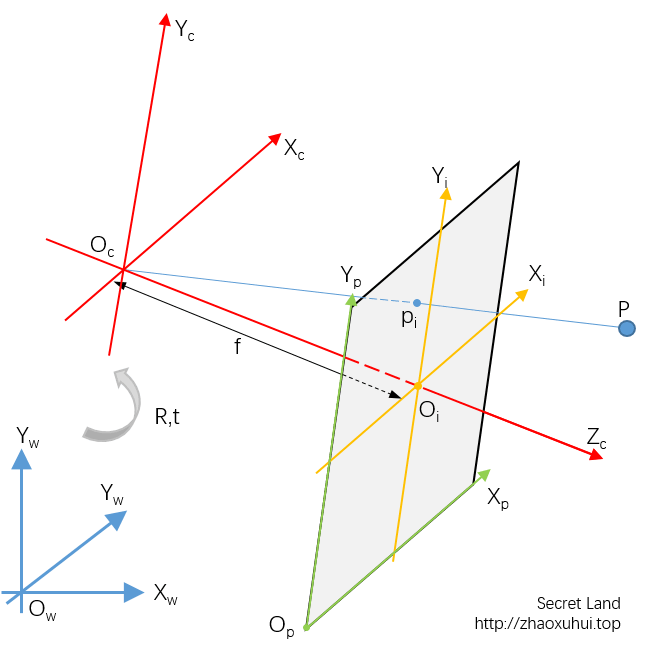这里为了易于区分直接以下标来区分不同的坐标系，并没有使用习惯的惯用表达(大X、小x等)。图中蓝色坐标系表示世界坐标系，红色坐标系表示相机坐标系，世界坐标系可以通过旋转、平移(R、t)变换到相机坐标系。橙色的坐标系为像平面坐标系，其原点为相机光心沿主光轴在像面上的投影，其与光心的距离就是相机焦距f。绿色的坐标系为像素坐标系。注意这里是以左下角为原点是因为本来像面应该是在相机光心后面的，而为了研究方便，所以把像面放到了光心前面，这样等于成的是倒像，所以这里的像素坐标再倒一下，原点就是左上角了。
5.坐标转换与成像模型
不同坐标系之间的转换在这篇博客中也有介绍，这里还是简单回顾一下。我们在说成像模型其实不外乎就是上面这几个坐标系之间的转换而已。首先我们需要明确的是成像模型的输入和输出(已知量和待求量)，也即要由什么坐标系转到什么坐标系。这样才能有整体概念，不至于糊涂。
从摄影测量的角度，图像的像素坐标是容易获得的。我们的目标是要是能知道一个点的像素坐标就能得到它在三维世界中的真实坐标就好了。所以可以理解为我们要的是从像素坐标转到世界坐标或者其逆过程。所以我们要寻找世界坐标与像素坐标的关系。根据上面的图，可以很容易得到下面的这个转换流程。
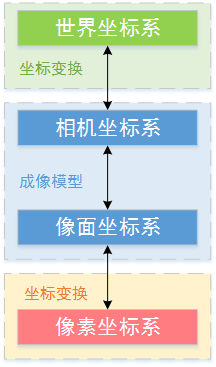
所以要想从像素坐标转到真实坐标需要两次坐标变换外加一次小孔成像模型(本质上也是坐标变换)。下面就分别介绍一下这三次变换。
(1)相机坐标系到像面坐标系(蓝色变换)
这是小孔成像模型的内容，相关原理与推导这里就不说了。详细可见刚刚提到的那篇博客。小孔成像模型的原理推导简单来说就是从三角形的相似性开始的。
假设某点P在相机坐标系下的坐标为 \((X,Y,Z)\) 其在像面上的坐标为 \((x,y)\) 。其实这里隐藏了个z分量，其值为焦距f，因为像面到光心的距离就是焦距。根据成像原理和三角形相似，可写出下面的公式：
\[\frac{X}{x}=\frac{Y}{y}=\frac{Z}{f}\]然后转换一下形式，用X、Y表示x、y(这里不管是用X、Y表示x、y还是反过来都是可以的，无非是得到了相反的转换关系)。
\[\left\{\begin{matrix} x=\frac{X}{Z}f\\ y=\frac{Y}{Z}f \end{matrix}\right.\]然后写成矩阵形式(需要用到齐次坐标，简单来说就是加一维，不然等式成立不了)
\[\begin{pmatrix} x\\ y\\ 1 \end{pmatrix}=\frac{1}{Z}\begin{pmatrix} f & 0 & 0\\ 0 & f & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X\\ Y\\ Z \end{pmatrix}\]把Z乘到等式左边来
\[Z\begin{pmatrix} x\\ y\\ 1 \end{pmatrix}=\begin{pmatrix} f & 0 & 0\\ 0 & f & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X\\ Y\\ Z \end{pmatrix}\]中间这个有焦距f的矩阵被称为相机的内参矩阵，单位为物理尺寸。它沟通了相机坐标系与像面坐标系之间的关系。
(2)像面坐标系转像素坐标系(粉色变换)
仔细观察之前的图可以发现，这两个坐标系之间其实是差了个平移与伸缩。因此直接利用坐标系的转换就能解决，与成像模型没关系。
设每个像素的物理尺寸大小为dx × dy(mm)(由于单个像素点投影在图像平面上是矩形而不是正方形，因此可能dx、dy不等)， 某点在像平面坐标系中的坐标为(x, y)，在像素坐标系中的坐标为(u, v)，则二者满足如下关系：
\[\left\{\begin{matrix} u = \frac{x}{dx}+u_0\\ v = \frac{y}{dy}+v_0 \end{matrix}\right.\]这里需要注意两点，一是为什么是除以dx而不是乘，这涉及到量纲的计算。 因为像面坐标x是有物理单位的，而dx表示一个像素代表多少实际物理尺寸，所以自然要拿(mm)/(mm/pixel)，这样才能得到量纲是pixel的数值。 二是可能会有疑问，如果按照上面的这个式子算，u、v很有可能是小数，像素坐标可能是小数吗？答案是可以的。 像素虽然都是整数，但也有亚像素的存在。经常听到精度是零点几个像素就是这样。 像素坐标系理论上并不一定非要是整数，只是在计算机保存的时候进行了离散化，可以这样理解。将上面的式子利用齐次写成矩阵形式如下
\[\begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\begin{pmatrix} \frac{1}{dx} & 0 & u_0\\ 0 & \frac{1}{dy} & v_0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x\\ y\\ 1 \end{pmatrix}\]这样便得到了像面坐标与像素坐标的转换关系。引入齐次坐标的目的主要是可以合并矩阵运算中的乘法和加法。
(3)世界坐标系转相机坐标系(绿色变换)
这个转换可以看作是两个刚体坐标系间的转换，十分简单，只需要知道相机在世界坐标系下的旋转R和平移t即可。假设某点在世界坐标系下的坐标为 \((X_w,Y_w,Z_w)\) ，在相机坐标系下的坐标为 \((X,Y,Z)\) 。那么很自然的有
\[\begin{pmatrix} X\\ Y\\ Z \end{pmatrix}=R\begin{pmatrix} X_w\\ Y_w\\ Z_w \end{pmatrix}+t\]当然可以把R、t合并成一个变换矩阵T，这里就不那样写了。这样便得到了世界坐标与相机坐标的关系。
(4)变换合并
在上面分别得到了每一步的变换后，自然可以将它们合并，这样便得到了真实世界坐标与像素坐标的关系。首先先将蓝色和粉色变换合并起来。
\[\begin{pmatrix} x\\ y\\ 1 \end{pmatrix}=\frac{1}{Z}\begin{pmatrix} f & 0 & 0\\ 0 & f & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X\\ Y\\ Z \end{pmatrix}\] \[\begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\begin{pmatrix} \frac{1}{dx} & 0 & u_0\\ 0 & \frac{1}{dy} & v_0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x\\ y\\ 1 \end{pmatrix}\]可以得到
\[\begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\begin{pmatrix} \frac{1}{dx} & 0 & u_0\\ 0 & \frac{1}{dy} & v_0\\ 0 & 0 & 1 \end{pmatrix}\frac{1}{Z}\begin{pmatrix} f & 0 & 0\\ 0 & f & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X\\ Y\\ Z \end{pmatrix}\]整理合并有
\[\begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\frac{1}{Z}\begin{pmatrix} \frac{f}{dx} & 0 & u_0\\ 0 & \frac{f}{dy} & v_0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X\\ Y\\ Z \end{pmatrix}\]这便是相机坐标系和像素坐标系的关系。这里含有f的矩阵也称为内参矩阵，记为K，其单位均为像素。再将其与绿色变换合并，有
\[\begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\frac{1}{Z}\begin{pmatrix} \frac{f}{dx} & 0 & u_0\\ 0 & \frac{f}{dy} & v_0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}R\begin{pmatrix} X_w\\ Y_w\\ Z_w \end{pmatrix}+t\end{pmatrix}\]这便是最终我们要的结果了。如果用T表示世界坐标系到相机坐标系的变换，用K表示内参矩阵，会简单一些。 其中f为相机焦距，单位一般是mm。dx,dy为像元尺寸。u0,v0为图像中心。fx = f/dx, fy = f/dy。分别称为x轴和y轴上的归一化焦距。
\[\begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\frac{1}{Z}KT\begin{pmatrix} X_w\\ Y_w\\ Z_w \end{pmatrix}\]等式两边乘以Z，有
\[Z\begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=KT\begin{pmatrix} X_w\\ Y_w\\ Z_w \end{pmatrix}\]看起来是个十分简单的式子，但其实并不简单。仔细回想我们的已有数据只是相机的内参和图像上的像素坐标。 这个式子根本没办法求解，不知道相机的变换矩阵T，不知道相机坐标。因此这个式子在实际应用中会根据不同情况进行化简。 如用归一化相机坐标(Z=1)代替相机坐标、把第一帧的相机坐标当作世界坐标(T=单位阵)等。 这样做虽然可以，但是就会有尺度损失的问题。这也对单目SLAM的尺度问题从原理上进行了解释。
二、相机畸变
上面说了这么多把成像模型和坐标变换说完了。下面进入另一个主题，就是相机畸变。 由于相机本身硬件的影像，相机都会有畸变，最直接的结果就是导致物体在成像平面上的坐标和由上面算出来的理论值不等了。 这对于摄影测量来说显然是不能容忍的。因此需要消除畸变。
1.相机畸变定义
(1)径向畸变
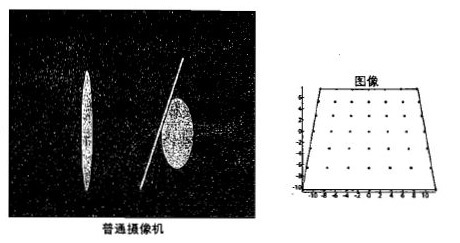
简单来说，由透镜形状引起的畸变称为径向畸变，径向畸变主要分为桶形畸变和枕型畸变。在针孔模型中，一条直线投影到像素平面上还是一条直线。
但在实际中，相机的透镜往往使得真实环境中的一条直线在图片中变成了曲线。越靠近图像的边缘现象越明显。
由于透镜往往是中心对称的，这使得不规则畸变通常径向对称。
(2)切向畸变
除了透镜的形状会引入径向畸变，在相机的组装过程中由于不能使透镜严格和成像平面平行，会引入切向畸变。
(3)畸变描述
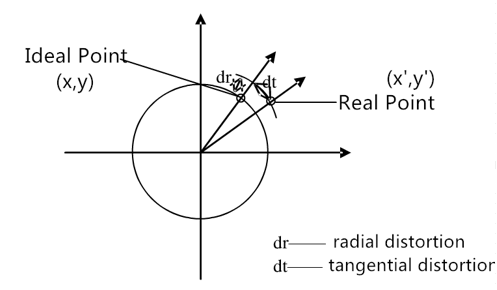
对于平面上任意点p，可以使用笛卡尔坐标描述为(x,y)，也可以使用极坐标描述为(r,θ)。r表示p点与原点的距离，θ表示其与水平轴的夹角。
对于径向畸变，可以看成坐标点沿着长度方向变化了Δr，对于切向畸变可以看成坐标点沿着切向方向发生了变化Δθ。
(4)畸变模型
对于径向畸变，它们都是随着与中心距离的增加而变大。因此可以用与距中心的距离有关的二次及高次多项式函数进行纠正。
\[\begin{matrix} x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)\\ y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6) \end{matrix}\]\(x_{distorted},y_{distorted}\)为像平面上真实观测到的坐标(含有畸变)，x、y是校正后点的坐标(不含畸变)。 对于畸变较小的中心区域，主要是\(k_1\)起作用，对于畸变较大的边缘，主要是\(k_2\)起作用。 普通摄像头用这两个系数就能很好地消除畸变了。对于畸变很大的摄像头，如鱼眼相机，可加入\(k_3\)消除畸变。
对于切向畸变，可以使用另外两个参数进行纠正。
\[\begin{matrix} x_{distorted}=x+2p_1xy+p_2(r^2+2x^2)\\ y_{distorted}=y+p_1(r^2+2y^2)+2p_2xy \end{matrix}\]利用上面两组式子就可对畸变进行较好的修正。同时对径向、切向畸变消除就是将两组式子合并。
\[\begin{matrix} x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)+2p_1xy+p_2(r^2+2x^2)\\ y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6)+p_1(r^2+2y^2)+2p_2xy \end{matrix}\]最终可以得到5个畸变参数
\[Distortioncoefficients = (k_1,k_2,p_1,p_2,k_3)\]畸变参数的一般顺序是\(k_1,k_2,p_1,p_2,k_3\)。之所以把\(k_3\)放在最后其实也很容易理解，因为前面说了一般\(k_1,k_2\)用来处理径向畸变足矣，\(k_3\)相对而言用的比较少。 在获得了畸变参数以后，也就找到了真实观测的带畸变的像素与无畸变的像素间的关系，重采样即可实现影像校正。
三、相机标定
上面说到了相机的镜头存在畸变，因此需要对其进行校正。确定相机内参和畸变模型中各系数的过程叫做相机标定。 这一部分也分为理论和实践两部分。
1.标定原理
在OpenCV中求解相机内参矩阵使用了张正友标定法，求解畸变参数是另外一个基于Brown的方法。对于张正友标定法的原理，这里就不说了，如果感兴趣可以参考这篇博客中的公式推导。求解畸变参数的原理这里简单提一下。在实际应用中更多只需要关注如何使用即可。
在通过张正友的方法获得了相机内参矩阵后，求解畸变系数，简单理解就是解方程。利用成像模型可计算获得“完美”的、符合成像模型的像平面坐标，而根据量测可以获得每一点真实对应的像平面坐标。由于有5个未知数，因此至少需要3对点(6个方程)，便可解出畸变参数。这就是上面提到的合并后的式子。
\[\begin{matrix} x_{corrected}=x(1+k_1r^2+k_2r^4+k_3r^6)+2p_1xy+p_2(r^2+2x^2)\\ y_{corrected}=y(1+k_1r^2+k_2r^4+k_3r^6)+p_1(r^2+2y^2)+2p_2xy \end{matrix}\]由完美的“成像模型”可以求解出\(x_{corrected},y_{corrected}\)(没有畸变时点应该在的位置)，现在因为有畸变，导致观测到的坐标为x、y。利用上面这个式子便可以求解。这里还有个参数r，这个r在上面提到是某点到极坐标原点的位置。由于现在内参已知，所以极坐标的原点设为(x0,y0)就可以知道。又有观测到的x、y，可以算出r。
\[r = \sqrt{(x-x_0)^2+(y-y_0)^2}\]2.OpenCV相机标定
在实际操作中我们可以使用OpenCV加棋盘格的方法对相机进行标定。一般情况下，用10-20张影像进行标定。
为了找到棋盘的图案，我们使用函数 cv2.findChessboardCorners()。在找到这些角点之后使用函数cv2.cornerSubPix()增加准确度。然后可以使用函数cv2.drawChessboardCorners()绘制图案。最后得到这些对象点和图像点之后使用cv2.calibrateCamera()进行标定。在标定结束后，相机的内参矩阵和畸变参数等相关参数会被返回。拿到相机内参、畸变参数等数据后，就可以用它们对相片进行校正，OpenCV中有cv2.undistort()可以很方便地实现这个需求。
在上面的流程中，其实标定的核心函数只是cv2.calibrateCamera()，前面那么多其实都是在做数据的准备。所以我们完全可以自己编写代码实现或者手工标注进行数据准备，例如有时OpenCV可找不到我们想要的棋盘格的时候。
OpenCV中校正函数的传入只是对应坐标，所以我们完全可以人工手动标记对应点坐标，再传入函数，同样可以进行标定。只是可能会比较麻烦点。
Python版代码如下：
import numpy as np
import cv2
import glob
ROWS = 6
COLOMONS = 7
# termination criteria
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((ROWS * COLOMONS, 3), np.float32)
objp[:, :2] = np.mgrid[0:ROWS, 0:COLOMONS].T.reshape(-1, 2)
print objp
# Arrays to store object points and image points from all the images.
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
images = glob.glob('*.jpg')
for fname in images:
img = cv2.imread(fname)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Find the chess board corners
ret, corners = cv2.findChessboardCorners(gray, (ROWS, COLOMONS), None)
# If found, add object points, image points (after refining them)
if ret == True:
objpoints.append(objp)
corners2 = cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)
imgpoints.append(corners2)
# Draw and display the corners
img = cv2.drawChessboardCorners(img, (ROWS, COLOMONS), corners2, ret)
cv2.imshow('img', img)
cv2.waitKey(500)
cv2.destroyAllWindows()
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
np.savetxt("inner.txt", mtx)
np.savetxt("distort.txt", dist)
print "Saved inner.txt"
print "Saved distort.txt"
for i in range(images.__len__()):
img = cv2.imread(images[i])
h, w = img.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (w, h), 1, (w, h))
# undistort
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)
# crop the image
x, y, w, h = roi
dst = dst[y:y + h, x:x + w]
cv2.imwrite("undistort_" + images[i], dst)
print "Undistorting...", (i + 1).__str__() + "/" + images.__len__().__str__()
在进行摄像机标定时我们要输入一组3D真实世界中的点以及与它们对应2D图像中的点。3D点被称为对象点，2D图像点被称为图像点。
2D图像点可以在图像中很容易的找到(这些点在图像中的位置是棋盘上两个黑色方块相互接触的地方)。而为了进行相机标定，我们必须要知道棋盘格的3D坐标。为了简单，可以说棋盘在 XY平面是静止的（所以Z总是等于0），摄像机在围着棋盘移动。 这种假设让我们只需要知道X，Y的值就可以了。
现在为了求X，Y的值，我们只需要传入这些点(0,0),(1,0),(2,0)…，它们代表了点的位置。 在这里使用的是OpenCV的示例图片，我们不知道方块的大小，所以只能采用“数格子”的方式。 但是如果我们知道单个方块的大小(如30mm)，我们输入的值就可以是(0,0),(30,0),(60,0)…，结果的单位就是mm。
下图是在某张相片中利用OpenCV识别出的棋盘格
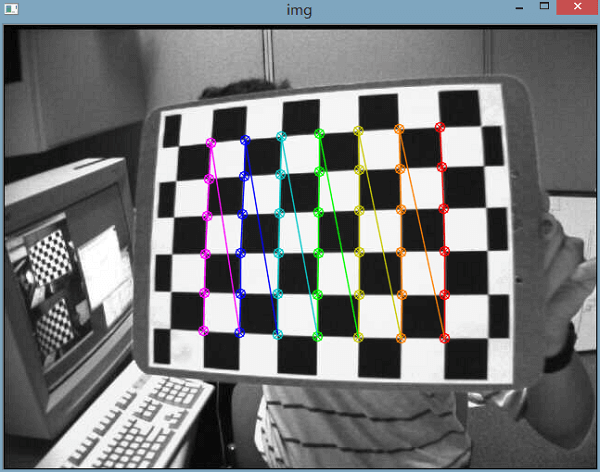
下面是输出保存的相机内参和5个畸变参数
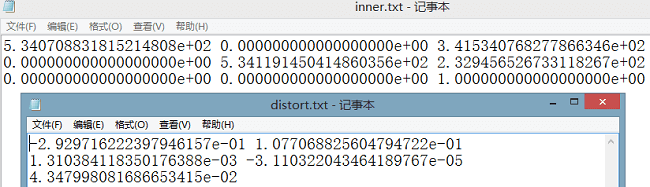
利用这些参数可以对相片进行校正，效果如下
六、参考资料
- https://www.cnblogs.com/Jessica-jie/p/6596450.html
- https://blog.csdn.net/yangdashi888/article/details/51356385
- https://blog.csdn.net/aptx704610875/article/details/48914043
- https://www.cnblogs.com/Undo-self-blog/p/8448500.html
- https://blog.csdn.net/dcrmg/article/details/52939318
本文作者原创,未经许可不得转载,谢谢配合
