1.神经网络数据分类
在这篇博客中，我们基于上篇博客所建立的神经网络对数据进行分类，代码如下。
import torch
from matplotlib import pyplot as plt
import torch.nn.functional as F
# 自定义一个Net类，继承于torch.nn.Module类
# 这个神经网络的设计是只有一层隐含层，隐含层神经元个数可随意指定
class Net(torch.nn.Module):
# Net类的初始化函数
def __init__(self, n_feature, n_hidden, n_output):
# 继承父类的初始化函数
super(Net, self).__init__()
# 网络的隐藏层创建，名称可以随便起
self.hidden_layer = torch.nn.Linear(n_feature, n_hidden)
# 输出层(预测层)创建，接收来自隐含层的数据
self.predict_layer = torch.nn.Linear(n_hidden, n_output)
# 网络的前向传播函数，构造计算图
def forward(self, x):
# 用relu函数处理隐含层输出的结果并传给输出层
hidden_result = self.hidden_layer(x)
relu_result = F.relu(hidden_result)
predict_result = self.predict_layer(relu_result)
return predict_result
# 训练次数
TRAIN_TIMES = 200
# 输入输出的数据维度
INPUT_FEATURE_DIM = 2
OUTPUT_FEATURE_DIM = 2
# 隐含层中神经元的个数
NEURON_NUM = 10
# 学习率，越大学的越快，但也容易造成不稳定，准确率上下波动的情况
LEARNING_RATE = 0.01
# 数据构造
# 先生成一个100行，2列的基础数据
n_data = torch.ones(100, 2)
# normal函数用于生成符合指定条件的正太分布数据，传入的参数是均值和标准差
x0 = torch.normal(2 * n_data, 1)
x1 = torch.normal(-2 * n_data, 1)
# 这里的y并不是y坐标的意思，而是代表数据的类型标签，是整个网络的输出，以0、1表示不同类别
# 输入：(x[0],x[1]) 输出：y
y0 = torch.zeros(100)
y1 = torch.ones(100)
# torch.cat是在合并数据,将a,b按行放在一起，如果第二个参数是0，则按列放在一起
x = torch.cat((x0, x1), 0).type(torch.FloatTensor) # FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor) # LongTensor = 64-bit integer
# 建立网络
net = Net(n_feature=INPUT_FEATURE_DIM, n_hidden=NEURON_NUM, n_output=OUTPUT_FEATURE_DIM)
print(net)
# 训练网络
# 这里也可以使用其它的优化方法
optimizer = torch.optim.Adam(net.parameters(), lr=LEARNING_RATE)
# 定义一个误差计算方法，分类问题可以采用交叉熵来衡量
loss_func = torch.nn.CrossEntropyLoss()
for i in range(TRAIN_TIMES):
# 输入数据进行预测
prediction = net(x)
# 计算预测值与真值误差，注意参数顺序问题
# 第一个参数为预测值，第二个为真值
loss = loss_func(prediction, y)
# 开始优化步骤
# 每次开始优化前将梯度置为0
optimizer.zero_grad()
# 误差反向传播
loss.backward()
# 按照最小loss优化参数
optimizer.step()
# 可视化训练结果
plt.cla()
prediction = torch.max(prediction, 1)[1]
pred_y = prediction.data.numpy().squeeze()
target_y = y.data.numpy()
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
accuracy = float((pred_y == target_y).astype(int).sum()) / float(target_y.size)
plt.text(-1, -4.7, 'Time=%d Accuracy=%.2f' % (i, accuracy), fontdict={'size': 15, 'color': 'red'})
plt.pause(0.1)
和之前代码相比，主要改动在数据生成和可视化部分，以及更换了代价函数。
同时为了演示减少了神经元个数和学习率，否则学习速度太快了，看不出变化的过程。
下面是运行的结果。
采用SGD算法。
采用Adam算法。可以发现Adam算法在30步左右即到了100%，而SGD算法在60步左右才100%。以上便是利用神经网络解决简单二分类问题的代码。
和上一篇的拟合相比，核心的神经网络架构都没有变化，只是修改了输入输出，但却实现了不同的功能。所以也可以体会到神经网络适用性还是比较广的。
关于torch中随机数生成的各种方法，可以参考这篇博客，总结地挺好的。
2.批训练
在之前TensorFlow的笔记中也提到过，相比于将数据整体放入网络训练，采用分批训练效果会更好一些。
在PyTorch中提供了DataLoader用于实现这个需求，放在torch.utils.data中。示例代码如下。
import torch
import torch.utils.data as Data
torch.manual_seed(1) # reproducible
BATCH_SIZE = 4 # 批训练的数据个数
x = torch.linspace(1, 10, 10) # x data (torch tensor)
y = torch.linspace(10, 1, 10) # y data (torch tensor)
# 先转换成 torch 能识别的 Dataset
torch_dataset = Data.TensorDataset(x, y)
# 把 dataset 放入 DataLoader
loader = Data.DataLoader(
dataset=torch_dataset, # torch TensorDataset format
batch_size=BATCH_SIZE, # mini batch size
shuffle=True, # 要不要打乱数据 (打乱比较好)
# 多线程来读数据，在windows下这句话可能会报错，如果报错就注释掉，可能是个bug
# num_workers=2,
)
for epoch in range(3): # 训练所有!整套!数据 3 次
for step, (batch_x, batch_y) in enumerate(loader): # 每一步 loader 释放一小批数据用来学习
# 假设这里就是你训练的地方...
# 打出来一些数据
print('Epoch: ', epoch, '| Step: ', step, '| batch x: ',
batch_x.numpy(), '| batch y: ', batch_y.numpy())
运行结果如下。
这里简单再说一下batch、batch size、step和epoch的关系。
对于一堆数据，我们可以将其分成好几份(Batch)来训练，每份中包含的数据个数即为batch size，每训练一份即是一个Step。
当把这几份全部训练完的时候也就是一个Epoch。
所以Epoch可以理解为从头到尾训练一遍全部数据的次数。
所以训练的总次数(输入输出一次数据算一次)等于Epoch×Batch Size×Batch。
例如一共有10个数据，分成5个batch，每个batch有两个数据，整体训练3次。
总次数就是2×5×3=30。
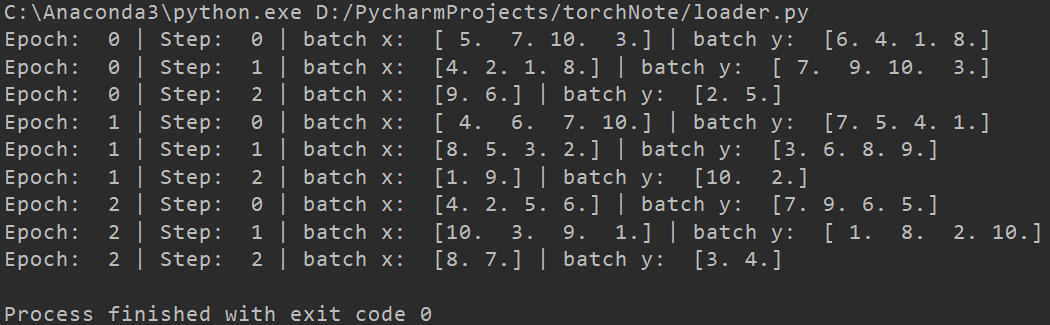
3.优化器
详细优化器介绍可参考教程。 SGD是最普通的优化器，也可以说没有加速效果，而Momentum是SGD的改良版，它加入了动量原则。 后面的后面的RMSprop又是Momentum的升级版，而Adam又是RMSprop的升级版。 但并不是越先进的优化器，结果越佳。我们在自己的试验中可以尝试不同的优化器，找到那个最适合你数据/网络的优化器。 下面代码分别用4种优化器进行训练。
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
LR = 0.1
# fake dataset
x = torch.unsqueeze(torch.linspace(-2, 2, 500), dim=1)
y = x.pow(3) + 0.1 * torch.normal(torch.zeros(*x.size()))
# default network
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(1, 20) # hidden layer
self.predict = torch.nn.Linear(20, 1) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
if __name__ == '__main__':
# different nets
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
# different optimizers
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []] # record loss
plt.figure(figsize=(10, 8))
# training
for step in range(200): # for each training step
output1 = net_SGD(x)
loss1 = loss_func(output1, y)
opt_SGD.zero_grad()
loss1.backward()
opt_SGD.step()
losses_his[0].append(loss1.data.numpy())
plt.subplot(221).cla()
plt.scatter(x.numpy(), y.numpy(), c='blue')
plt.plot(x.numpy(), output1.data.numpy(), c='red')
plt.title('SGD,Time=%d Loss=%.4f' % (step, loss1.data.numpy()))
output2 = net_Momentum(x)
loss2 = loss_func(output2, y)
opt_Momentum.zero_grad()
loss2.backward()
opt_Momentum.step()
losses_his[1].append(loss2.data.numpy())
plt.subplot(222).cla()
plt.scatter(x.numpy(), y.numpy(), c='blue')
plt.plot(x.numpy(), output2.data.numpy(), c='red')
plt.title('Momentum,Time=%d Loss=%.4f' % (step, loss2.data.numpy()))
output3 = net_RMSprop(x)
loss3 = loss_func(output3, y)
opt_RMSprop.zero_grad()
loss3.backward()
opt_RMSprop.step()
losses_his[2].append(loss3.data.numpy())
plt.subplot(223).cla()
plt.scatter(x.numpy(), y.numpy(), c='blue')
plt.plot(x.numpy(), output3.data.numpy(), c='red')
plt.title('RMSprop,Time=%d Loss=%.4f' % (step, loss3.data.numpy()))
output4 = net_Adam(x)
loss4 = loss_func(output4, y)
opt_Adam.zero_grad()
loss4.backward()
opt_Adam.step()
losses_his[3].append(loss4.data.numpy())
plt.subplot(224).cla()
plt.scatter(x.numpy(), y.numpy(), c='blue')
plt.plot(x.numpy(), output4.data.numpy(), c='red')
plt.title('Adam,Time=%d Loss=%.4f' % (step, loss4.data.numpy()))
plt.pause(0.1)
labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
for i, l_his in enumerate(losses_his):
plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.show()
学习率为0.1，训练200次运行效果如下。
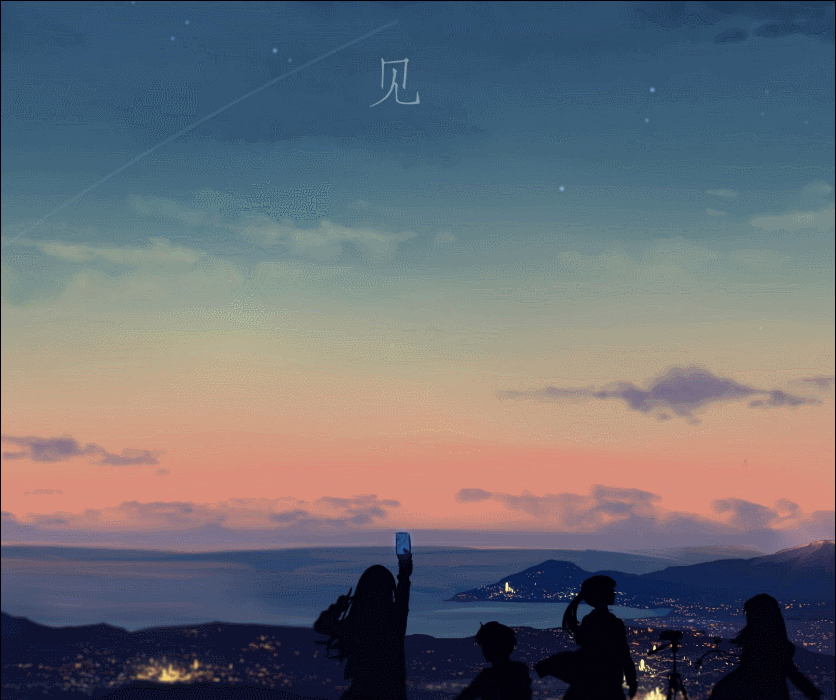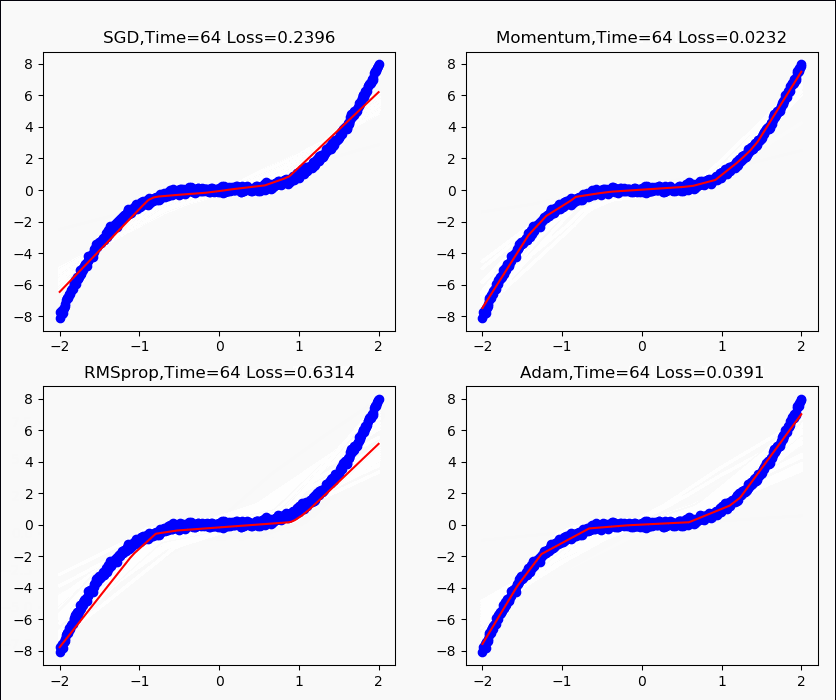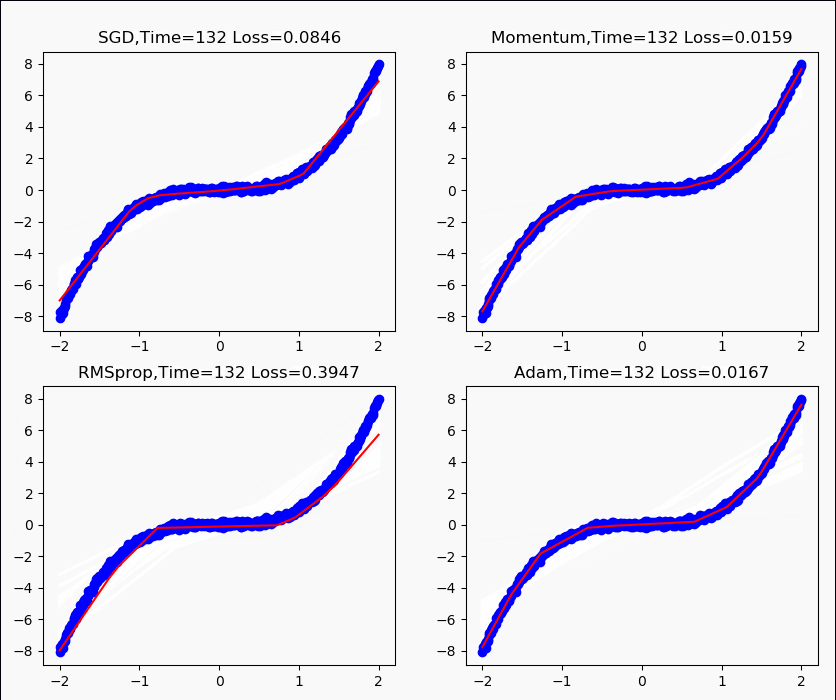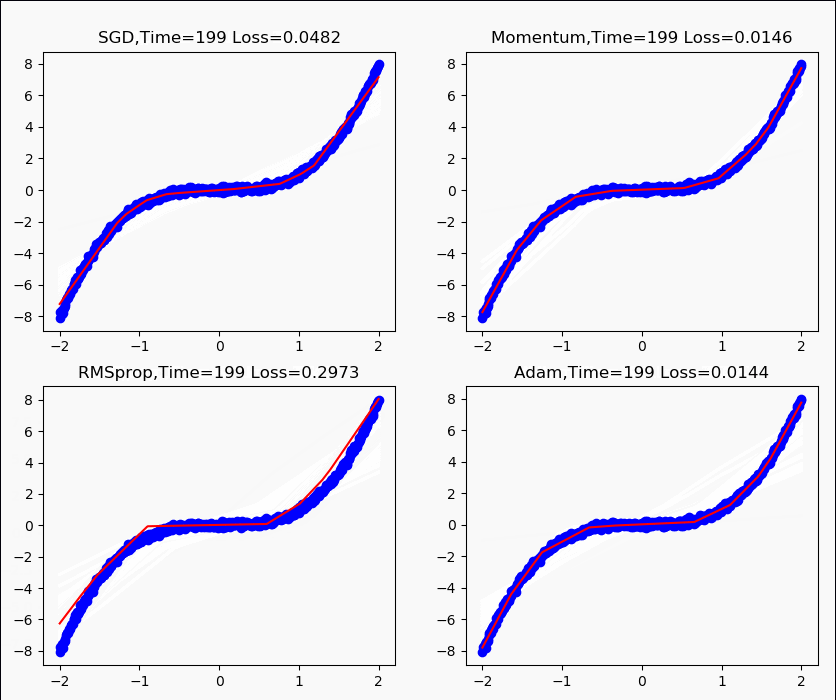以及不同方法收敛速度对比图如下。
此外，也用教程中给出的代码采用分批训练跑了一下，代码如下。
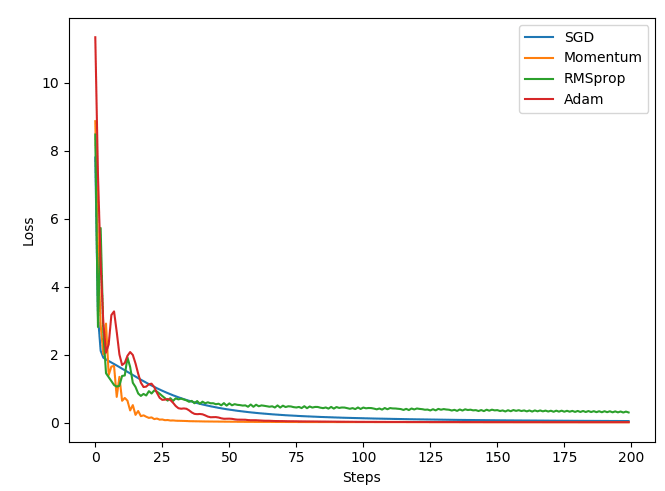
import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt
# torch.manual_seed(1) # reproducible
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12
# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))
# # plot dataset
# plt.scatter(x.numpy(), y.numpy())
# plt.show()
# put dateset into torch dataset
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)
# default network
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(1, 20) # hidden layer
self.predict = torch.nn.Linear(20, 1) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
if __name__ == '__main__':
# different nets
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]
# different optimizers
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]
loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []] # record loss
# training
for epoch in range(EPOCH):
print('Epoch: ', epoch)
for step, (b_x, b_y) in enumerate(loader): # for each training step
for net, opt, l_his in zip(nets, optimizers, losses_his):
output = net(b_x) # get output for every net
loss = loss_func(output, b_y) # compute loss for every net
opt.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
opt.step() # apply gradients
l_his.append(loss.data.numpy()) # loss recoder
labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
for i, l_his in enumerate(losses_his):
plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()
结果如下。
本文作者原创,未经许可不得转载,谢谢配合
