0.猜想
在之前和同学讨论问题的时候聊到了遥感卫星的地表分辨率会不会随着卫星的高度而改变这个问题。在此之前从来没有考虑过这个问题,因为卫星的地表分辨率很多时候都是作为一个定值给出的,所以就理所当然地认为是不会变的。但这个“理所当然”正确与否便是本篇博客讨论的问题之一。 另一个问题是影像中像素的地表分辨率会不会随着像素的位置不同而不同,是不是有中间像素分辨率高,越往边缘地表分辨率越低的情况。这是本博客讨论的第二个问题。为了解答以上两个问题,下面便从公式进行推导。
1.公式与理论推导
已知O为相机光心,OI为相机光心到像面的距离,即焦距\(f\);OJ为相机光心到物体的垂直距离\(h\)。∠IOA为当前像素与光心连线和主光轴的夹角,其可以根据焦距\(f\)以及像素索引(位置)算出,后续为使用方便记为\(α\),它的对顶角∠COJ记为\(β\)。AB、EF的长度为\(p\),代表一个像素的实际大小(物理长度),CD、GH为一个像素对应实际物体的长度,记为\(d\)。如下图所示。
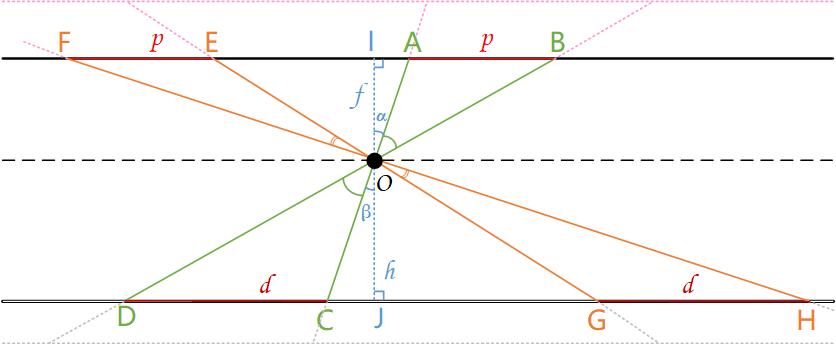
我们的目的是求得CD以及GH的表达式,探究其与不同位置像素的关系。
由三角形相似原理可知△ABO与△CDO相似,则有下式:
\[\frac{AB}{CD}=\frac{AO}{CO}=\frac{BO}{DO}\]因此CD可以通过下式求出:
\[CD=\frac{AB\cdot CO}{AO}=p\cdot \frac{CO}{AO}\]而在直角三角形△AIO和△COJ中,结合已知量根据余弦公式有:
\[cos\alpha=\frac{f}{AO},cos\beta = \frac{h}{CO}\]稍作整理有:
\[AO=\frac{f}{cos\alpha},CO = \frac{h}{cos\beta}\]CO和AO的比值为:
\[\frac{CO}{AO}=\frac{h}{cos\beta}\cdot \frac{cos\alpha}{f}=\frac{h}{f}\]CD可按下式计算:
\[CD = p \cdot \frac{h}{f}\]同理,可以推导得出GH的公式为:
\[GH = p \cdot \frac{h}{f}\]因此最终单像素长度\(p\)(在遥感中又被称作探元大小)与其代表的物体长度\(d\)之间的关系如下式所示:
\[d = p \cdot \frac{h}{f}\]由公式可以看出某个像素所代表的物体的长度(单像素分辨率m/pixel)仅与焦距\(f\)和距离物体的垂直距离\(h\)有关(相机感光元件不变的情况下),与像素在像平面内的位置无关。
在\(h\)不变的情况下,增加焦距\(f\)会使每个像素代表的物体长度减少(如图中粉色虚线所示,每个像素代表的物体长度未增加,但对应像素的长度增加了,等价于每个像素代表的物体长度减少)。对于遥感卫星而言也即地表分辨率的上升(数值变小了,如从2m/pixel变成1m/pixel),可以看到更多细节了。
在\(f\)不变的情况下,增加到物体的距离\(h\)会使每个像素代表的物体长度增加(如图中灰色虚线所示,像素本身长度没变,但其代表的物体长度增加了)。对于遥感卫星而言也即地表分辨率的下降(数值变大了,如从1m/pixel变成2m/pixel),对细节的分辨能力下降了。
从另一个角度考虑,若已知\(p\)、\(h\)、\(f\)即可以根据上述公式计算出图像中一个像素所代表的物体实际长度,通过统计物体共有多少个像素,即可计算出物体的真实长度,做成“相机尺子”。
2.遥感中的应用
由于遥感中的地表分辨率一般说地表分辨率越高就是地表分辨率数值越小的意思,和上式是相反的关系,为了使用方便不妨对上式加个负号,定义地表细节分辨能力,如下:
\[cap_{reso}=-d=-p \cdot \frac{h}{f}\]增大\(f\)使地表细节分辨能力上升,地表分辨率数值降低;增大\(h\)使地表细节分辨能力下降,地表分辨率数值上升。上式告诉我们三件事情:
-
(1)遥感影像中每个像素的地表分辨率都相同,与其在影像中的位置无关(不考虑镜头畸变)。
-
(2)卫星的地表分辨率并非卫星的固有属性、固定不变,而是随着拍摄状态不停变化,且只与焦距\(f\)、距地表垂直距离\(h\)以及探元大小\(p\)有关。
-
(3)在相机硬件条件不变的情况下,地表细节分辨能力随着垂直距离\(h\)的减小而逐渐增强,随着\(h\)的增加而逐渐减弱。
以上三条结论可以让我们更清晰地理解卫星地表分辨率这个概念以及指导我们对卫星的设计与理解。如想获得更高的地表细节分辨能力,在条件允许的情况下应尽可能降低轨道高度同时使用更大的焦距。而对于高轨卫星,要想获得同低轨卫星相同的地表细节分辨能力,则必须采用更大的焦距。
3.其它情况
以上讨论的都是像平面与物体所在平面或地表平行的情况,另一种需要讨论的是像平面与地表不平行时像素地表分辨率的变化情况,如下图所示。
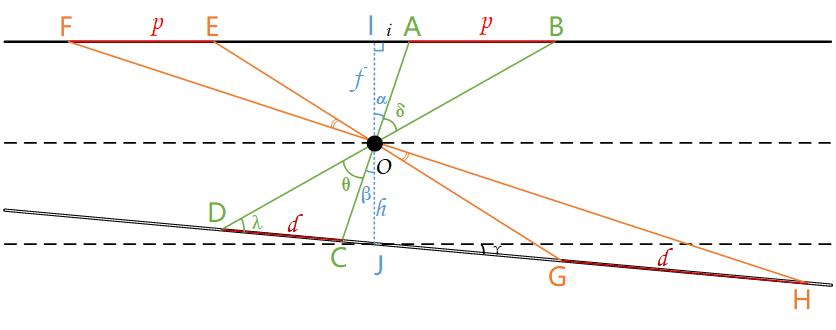
为了后续推导方便,在图1的基础上新增了几个定义。像素AB的位置索引记为\(i\)(IA的长度),地面旋转的角度记为\(\gamma\),∠AOB=∠COD=δ=θ,∠ODC记为\(\lambda\)。
我们的最终目的是求CD的长度\(d\),下面开始推导,推导主要用到三角函数、反函数、正弦定理等相关知识。
首先计算α和δ。在直角三角形△IOA中有:
\[tan\alpha = \frac{i}{f}\]因此根据反函数可求出:
\[\alpha=\beta = arctan(\frac{i}{f})\]同理在直角三角形△IOB中,有:
\[tan(\alpha+\delta)=\frac{i+p}{f}\] \[\alpha+\delta=arctan(\frac{i+p}{f})\]因此可得:
\[\delta=\theta = arctan(\frac{i+p}{f})-arctan(\frac{i}{f})\]为了求出CD长度需要先求出OC的长度。在三角形△OCJ中,根据正弦定理有:
\[\frac{sin\beta}{CJ}=\frac{sin\angle OCJ}{h}=\frac{sin\angle OJC}{OC}\]要求得OC,必须要知道∠OJC以及∠OCJ。将其局部放大便可以很容易根据几何知识求得,如下图:
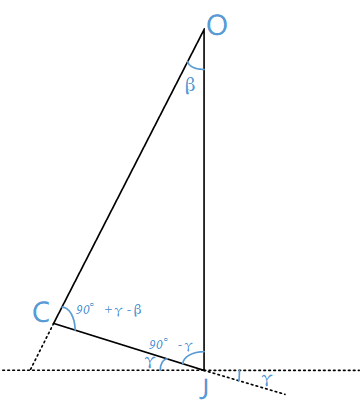
可得:
\[\angle OJC=90^{\circ}-\gamma\] \[\angle OCJ=180^{\circ}-\beta-(90^{\circ}-\gamma)=90^{\circ}+\gamma-\beta\]因此:
\[\frac{sin(90^{\circ}-\gamma)}{OC}=\frac{sin(90^{\circ}+\gamma-\beta)}{h}\] \[OC = \frac{sin(90^{\circ}-\gamma)\cdot h}{sin(90^{\circ}+\gamma-\beta)}\]在三角形△OCD中有:
\[\angle DCO=180^{\circ}-\angle OCJ=90^{\circ}-\gamma+\beta\] \[\angle ODC = \lambda = 180^{\circ}-\angle DOC-\angle DCO=90^{\circ}-\beta+\gamma-\theta\]再次运用正弦定理有:
\[\frac{sin\theta}{CD}=\frac{sin\lambda}{OC}=\frac{sin\angle DCO}{DO}\]可得:
\[\frac{sin\theta}{CD}=\frac{sin\lambda}{OC}\] \[CD = d = \frac{sin\theta \cdot OC}{sin\lambda}\]至此便得到了求解CD长度的公式,将上面重要的公式再罗列一下如下:
\[\alpha=\beta = arctan(\frac{i}{f})\] \[\delta=\theta = arctan(\frac{i+p}{f})-arctan(\frac{i}{f})\] \[OC = \frac{sin(90^{\circ}-\gamma)\cdot h}{sin(90^{\circ}+\gamma-\beta)}\] \[CD = d = \frac{sin\theta \cdot OC}{sin\lambda}\]将OC带入CD公式可得:
\[CD = d = \frac{sin\theta sin(90^{\circ}-\gamma)\cdot h}{sin(90^{\circ}+\gamma-\beta)sin(90^{\circ}+\gamma-\beta-\theta)}\]利用两角和差公式对上式进行化简,如下:
\[CD = d = \frac{sin\theta cos\gamma\cdot h}{cos(\gamma-\beta)cos(\gamma-\beta-\theta)}\]上式便是影像上单个像素代表的物体长度随旋转的变化关系,相对复杂。
4.结论
经过上面的一系列公式推导,至此可以对本文开头提出的两个问题进行回答了。
先回答第二个问题:像素的地表分辨率是否会因为像素在影像中的位置不同而有所变化?答案是不会。原因就是前面推导出来的公式,其只与像素本身大小\(p\)、焦距\(f\)以及距离地面垂直距离\(h\)有关,与其它因素无关。
对于第一个问题:卫星地表分辨率是否会因为高度变化而变化?答案是会。这里以珠海一号视频星(OVS-1)为例,进行说明,相关卫星参数如下所示。

首先可以根据公式验证分辨率,由参数可知:
\[f=1.5362m,h=550000m,p=5.5 \times 10^{-6}m\]带入公式:
\[d = p \cdot \frac{h}{f}\]可以解得此条件下卫星的地表分辨率为1.96914m,与标称的1.98m基本吻合,不完全吻合的原因是给出的参数不一定精确。如果按照给出的地表分辨率反推轨道高度,可以算出轨道高度是553.032km。也可以绘制出在\(f\)和\(p\)固定的情况下,地表分辨率随高度变化的图像,如下:
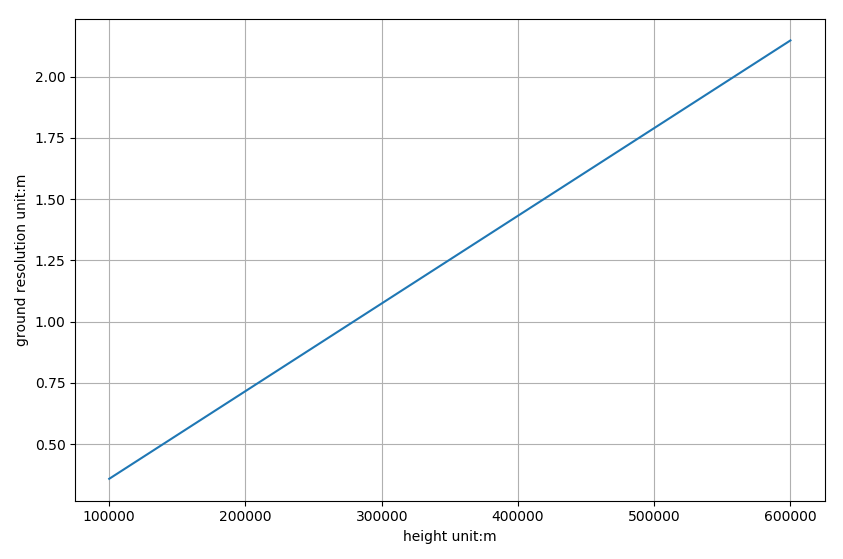
在成像硬件条件不变的情况下,增大轨道高度\(h\),地表分辨率数值增加,地表细节分辨能力降低,两者成正比关系。而在轨道高度不变的情况下,增大焦距\(f\),会使地表分辨率数值下降,地表细节分辨能力上升,两者成反比关系。
进一步可以对上述公式进行敏感度分析,更加仔细研究在焦距、像素大小等硬件条件不变情况下,轨道高度\(h\)对地表分辨率的影响,可以发现其函数是一个形如y=kx的单调增函数,对其求导可得系数k即为\(\frac{p}{f}\)。因此改变\(h\),地表分辨率变化的快慢主要取决于\(\frac{p}{f}\)。以珠海一号为例,可以求出当轨道高度改变了100km时,地表分辨率的变化为0.358m。但一般卫星到达设计轨道后就基本不会做大幅度的变轨(这会消耗大量的燃料)。因此对于卫星而言,其地表分辨率随高度变化的波动范围较小,再加上卫星一般不会轻易大幅变动轨道,因此某种程度上也可以认为是定值,这是合理的。
本文作者原创,未经许可不得转载,谢谢配合
