Eigen学习与使用笔记1

1.库的安装
2.CMake中库的声明与使用
3.代码中头文件引用与简单示例
4.Eigen中的矩阵与向量
5.Eigen中的矩阵运算
- (1)加减乘除
- (2)矩阵本身运算
6.Eigen中的Array
7.Eigen中的矩阵块操作
- (1)常规操作
- (2)其它特殊操作
8.Eigen中的Map
9.其它操作
10.参考资料

Eigen是一个非常优秀的开源矩阵运算及线性代数库，熟练掌握Eigen十分有用。“eigen”这个单词本身的意思是“特征、本征”，读作[‘eɪdʒən]，例如矩阵的特征值英文就是“eigen value”。本篇博客即从使用角度介绍一下Eigen一些基本用法。以下内容均根据我个人使用情况所编写，不一定完全正确，部分观点以及方法仅供参考。

1.库的安装

关于如何安装Eigen库，在之前博客中也有提到过，在Linux下一行命令即可搞定。

apt install libeigen3-dev

2.CMake中库的声明与使用

由于Eigen本身全部是头文件，所以在CMake项目中就不需要target_link_libraries了，只需要find_package，然后再include_directories即可。下面是CMakeLists.txt中完整的代码。

# CMake要求本版信息即项目名称，创建时自动生成
cmake_minimum_required(VERSION 3.12)
project(useEigen)

# 申明采用C++11标准，项目创建时自动生成
set(CMAKE_CXX_STANDARD 11)

# 寻找Eigen库
find_package(Eigen3 REQUIRED)
# 将Eigen库include进来
include_directories(${EIGEN3_INCLUDE_DIRS})

add_executable(${PROJECT_NAME} main.cpp)

需要注意的是，在find_package的时候，必须要写成Eigen3，而不能写成eigen、eigen3、EIGEN、EIGEN3、Eigen等，否则会报找不到库的错误(Could not find a package configuration file)。所以如果你在用Eigen的时候出现了找不到库的情况，先别怀疑是不是没有安装好，而是应该先检查是不是CMake文件里写的库名字不对。因为一般情况下，使用apt安装只要不报错都是没问题的。

第二个需要注意的是在include_directories时，同理只能写成EIGEN3_INCLUDE_DIRS而不是其它形式，如EIGEN3_INCLUDE_DIRECTORIES、Eigen3_INCLUDE_DIRS等，否则CMake检查时是可以通过的，但是编译时就会提醒找不到头文件。所以和上面一样，如果在编译时提示找不到相关头文件，先检查一下是不是CMake文件里包含目录写的不对。

3.代码中头文件引用与简单示例

经过第二步在CMake中配置好包含路径后，下面就要开始正式写代码了。一般情况下需要引入<Eigen/Dense>头文件(最为基础)，它主要用于处理一些与稠密矩阵运算相关的函数。同时为了使用方便，会使用Eigen命名空间。示例代码如下。

#include <iostream>
#include <Eigen/Dense>

using namespace std;
// 使用Eigen命名空间
using namespace Eigen;

int main() {
    // 以Xd方式声明一个3x3的矩阵
    MatrixXd mat(3, 3);
    // 将矩阵(0,0)位置元素赋为1.3
    mat(0, 0) = 1.3;
    cout << mat << endl;
    return 0;
}

这样编译运行结果如下所示。这里需要注意的是MatrixXd这个类型的意思是一个动态大小的矩阵，X代表大小不确定，d表示数据类型是double，注意d并不是dimension(维度)的缩写。所以Matrix3d的意思并不是说是一个3维的矩阵，正确的意思是表示一个3X3的double类型的矩阵。与之对应的还有Matrix3f、Matrix3i、Matrix3cd等，这些都大同小异，表示数据类型分别是float、int以及double型的复数。在Eigen中为了使用方便，已经预定义好了很多这种类型，我们直接调用即可。根据文档的表述，对于小于等于4的矩阵建议用固定大小矩阵，大于4的推荐动态矩阵。（A rule of thumb is to use fixed-size matrices for size 4-by-4 and smaller.）更详细的内容后续介绍。

4.Eigen中的矩阵与向量

本部分主要介绍Eigen中矩阵与向量的定义及基本使用。在Eigen中，所有的矩阵与向量都是Matrix模板类的对象，向量可以理解为是矩阵的行或列为1时的特殊情况。

(1)创建

一般而言，创建一个矩阵需要调用Matrix<>构造，其共包含6个参数，前三个为必须参数，后三个为可选参数，有默认值。三个必须参数如下：

Matrix<typename Scalar, int RowsAtCompileTime, int ColsAtCompileTime>

简而言之第一个参数指定矩阵的数据类型：double、float、int…，第二和第三个参数分别表示矩阵的行数与列数。因此一个简单的矩阵声明如下：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    Matrix<double, 5, 3> m1;
    cout << m1 << endl;
    return 0;
}

上述代码定义了一个长得比较“奇怪”的矩阵m1，并且输出到控制台。结果如下：可以看到新建一个矩阵的时候，如果不赋初值，默认全为0。

上述代码可以构建出任意形状的矩阵，好用是好用，就是有些麻烦。Eigen也考虑到了这一点，因此对于一些常用大小的矩阵Eigen已经帮我们提前定义好了，我们只需要用就可以了。这个在上一部分已经说过了，这里就不再赘述。

而对于向量，其创建方式与矩阵完全一样(包括预定义的常用大小向量)，不同的就是把Matrix换成Vector，这样新建的默认都是列向量，如果需要新建行向量，关键词换成RowVector即可。

上面介绍的都是大小在编译前就确定的矩阵，这种矩阵可以称为固定矩阵(fixed matrix)，另一种是编译前大小不确定的矩阵，称为动态矩阵(dynamic matrix)。对于这种情况，可以使用Dynamic关键字。需要注意的是尖括号里只能是常量，不能传入变量，像下面这样写是会报错的，编译都过不了。

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    int a = 3;
    int b = 7;
    Matrix<double, a, b> m;
    return 0;
}

到这里你可能会好奇，既然不能以传入变量的方式动态创建矩阵，那怎么控制矩阵大小呢？答案是利用矩阵的resize()函数。从字面意思就知道这个函数是用来改变矩阵大小的。因此上面这段代码可以这样改写：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    int a = 3;
    int b = 7;
    Matrix<double, Dynamic, Dynamic> m;
    m.resize(a, b);
    return 0;
}

但需要注意的是resize()这个函数是”毁灭性”(destructive)的，改变大小以后矩阵元素会改变。所以它一般只用来对动态矩阵做初始化。而我们认为的改变大小的功能对应conservativeResize()函数。顺带一提，如果矩阵变大了，多余的元素为0。

当然更一般和方便的方式是采用一些预定义好的类，如下。

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    int a = 10;
    int b = 3;
    MatrixXi m(a, b);
    return 0;
}

上述代码即声明了一个动态大小的矩阵m。

(2)初始化

在Eigen中可以方便的使用逗号初始化语法(comma-initializer syntax)，如下。

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    Matrix3d m;
    m << 1, 2, 3,
            4, 5, 6,
            7, 8, 9;
    cout << m << endl;
    return 0;
}

输出如下：

需要注意两点：一是在Eigen中初始值默认都是先列后行的，即按顺序读取初始值，依次填充矩阵，直到把第一行填满了再填下一行；二是初始值的个数必须严格对应矩阵大小，如上面3x3的矩阵共有9个元素就必须要有9个初始值，一个萝卜一个坑，多了少了都会报赋值失败的错误。

除了依次输入元素数值外，逗号初始化语法也支持向量以及矩阵的拼接。

(3)矩阵元素操作与矩阵大小获取

在Eigen中用()获取矩阵或向量中的元素，如m(4,7)就表示获取4行7列的元素，简单易懂。而对元素的修改则更简单，获取到元素后直接赋值即可。

此外，矩阵分别有.rows()、.cols()、.size()函数来分别获取矩阵的行数、列数以及元素个数。.data()函数用于返回一个指向矩阵或向量的首地址的指针。

(4)小技巧

以上是一些常规“操作”，下面介绍一些方便使用的函数。在创建矩阵时，还有一些非常方便的函数，这里简单介绍一下。

MatrixXd::Random(m,n)：创建m×n维double类型的随机数矩阵
MatrixXd::Constant(m,n,p)：创建m×n维double类型元素全为p的矩阵
MatrixXd::Zero(m,n)：创建m×n维元素全为0的矩阵
MatrixXd::Ones(m,n)：创建m×n维元素全为1的矩阵
MatrixXd::Identity(m,n)：创建m×n维的单位阵
VectorXd::LinSpaced(size,low,high)：创建一个size长度的从low到high的向量或一维矩阵

部分演示如下：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    MatrixXd m1 = MatrixXd::Random(5, 2);
    Matrix3d m2 = Matrix3d::Constant(8);
    return 0;
}

5.Eigen中的矩阵运算

(1)加减乘除

这一部分主要包含稠密矩阵的相关运算。由于Eigen重载了基本的+、-、×运算符，因此可以比较方便地进行运算。需要注意的一点是Eigen对数据类型敏感，并且不会自动类型转换，如自动将float转成double等。因此一个Matrix3d和一个Matrix3f相乘是会报错的。另一点需要注意的是+、-运算符不支持矩阵直接和标量运算，只支持相同大小的矩阵进行运算。遇到如对一个矩阵的每个元素同时减去或加上某个值时可以构造出一个与运算矩阵相同大小的单值矩阵即可。如下示例新建了一个动态矩阵并进行了元素级的减法运算。

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    MatrixXd m1(3, 2);
    m1 << 4, 5, 8, 3, 5, 0;
    cout << m1 << endl;
    MatrixXd m2(m1.rows(), m1.cols());
    m2 = m1 - MatrixXd::Constant(m1.rows(), m1.cols(), 1.2);
    cout << m2 << endl;
    return 0;
}

而对于乘法既可以和标量相乘(每个元素都乘以这个数)、也可以和矩阵相乘(常规矩阵乘法)。对于除法，只能用于矩阵和标量，表示把每个元素都处以某个数。总结如下：

加法：只能用于相同大小矩阵
减法：只能用于相同大小矩阵
乘法：矩阵与标量、矩阵与矩阵
除法：只能用于矩阵与标量

对于向量的点乘和叉乘分别有函数vector.dot()和vector.cross()，使用示例如下：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    Vector3d v(1, 2, 3);
    cout << "ori vector:\n" << v << endl;
    cout << "* result:\n" << v * 3 << endl;
    cout << "dot result:\n" << v.dot(v) << endl;
    cout << "cross result:\n" << v.cross(v) << endl;
    return 0;
}

输出结果如下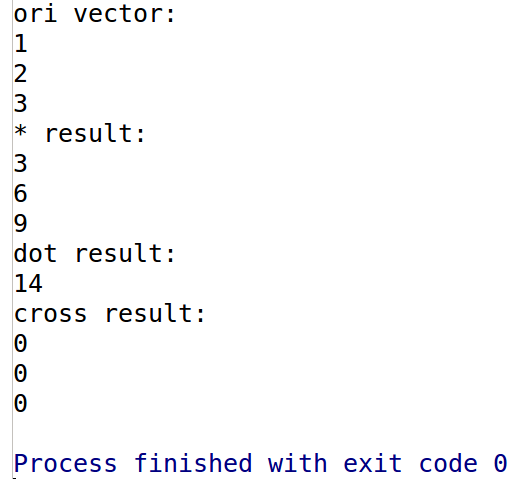：这里简单复习下向量的乘法运算，向量一共有3种乘法：标量积、点积和叉积。标量积即每个分量乘以相同数，结果还是一个向量，对应向量的缩放。点积是两个向量每个分量对应相乘再相加，结果为标量，两个向量之间的夹角，以及在b向量在a向量方向上的投影。叉积是将两个向量按叉积公式展开相乘，结果仍然是一个向量，并且两个向量的叉积与这两个向量组成的坐标平面垂直。

(2)矩阵本身运算

在Eigen中，对于输入是矩阵或数组，返回是标量的函数叫做Reduction。

mat.transpose()：转置矩阵。对于矩阵转置，注意不要写成a = a.transpose()，这会导致错误结果(Aliasing Issue)，如果一定需要对原矩阵进行修改，使用a.transposeInPlace()函数。
mat.inverse()：逆矩阵
mat.conjugate()：共轭矩阵
mat.adjoint()：伴随矩阵
mat.trace()：矩阵的迹
mat.eigenvalues()：矩阵的特征值
mat.determinant()：矩阵求行列式的值
mat.diagonal()：矩阵对角线元素
mat.sum()：矩阵所有元素求和
mat.prod()：矩阵所有元素求积
mat.mean()：矩阵所有元素求平均
mat.minCoeff()：矩阵所有元素最小值
mat.minCoeff(&i,&j)：矩阵所有元素最小值的位置，i、j为int类型或为Eigen的Index类型。
mat.maxCoeff()：矩阵所有元素最大值
mat.maxCoeff(&i,&j)：矩阵所有元素最大值的位置
mat.nonZeros()：矩阵中非零元素个数
mat.squaredNorm()：矩阵(向量)的平方范数，对向量而言等价于其与自身做点积，数值上等于各分量的平方和。
mat.norm()：矩阵(向量)的平方范数开根号(对于向量即求模长)
mat.lpNorm<1>()：矩阵(向量)的L1范数
mat.lpNorm<2>()：矩阵(向量)的L2范数
mat.lpNorm<Infinity>()：矩阵(向量)的L无穷范数
mat.lpNorm<p>()：矩阵(向量)的Lp范数
mat.normalize()：矩阵(向量)的正则化(归一化)，使所有元素的平方和等于1。
(mat>0).all()：矩阵元素条件判断，mat中所有元素是否都大于0，是返回1，否则返回0。
(mat>0).any()：矩阵元素条件判断，mat中所有元素是否有大于0的，有返回1，否则返回0。
(mat>0).count()：矩阵符合条件的元素计数，返回mat中大于0元素的个数。
mat.colwise()：返回矩阵每列的值
mat.rowwise()：返回矩阵每行的值

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    int i, j;
    double max_val;
    MatrixXd m = MatrixXd::Random(4, 7);
    max_val = m.maxCoeff(&j, &j);
    cout << m << endl;
    cout << max_val << "@" << i << "," << j << endl;
    return 0;
}

利用上述代码即可以非常方便地返回矩阵的最大值以及所在位置。

float maxNorm = mat.colwise().sum().maxCoeff(&maxIndex);

利用这个可以写出计算矩阵1范数的代码。

这里简单介绍一下范数的算法，分为向量和矩阵两部分。对向量而言：

向量的1-范数为各元素绝对值之和。
向量的2-范数为各元素平方和再开根号。
向量的正无穷范数为各元素绝对值的最大值、负无穷范数为各元素绝对值的最小值。

对矩阵而言，注意区别1-范数、2-范数和L1范数、L2范数，是不同的概念。

矩阵的1-范数又称为列模，为每一列上的元素绝对值先求和，再从中取出最大值。
矩阵的2-范数又称为谱模，为ATA的最大特征值开平方。
矩阵的无穷范数又称为行模，为每一行上的元素绝对值先求和，再从中取出最大值。
矩阵的核范数是矩阵的奇异值（将矩阵svd分解）之和。
矩阵的L0范数是矩阵中非0元素的个数，通常用它来表示稀疏，L0范数越小0元素越多，也就越稀疏。
矩阵的L1范数是所有元素绝对值之和，又被称为曼哈顿距离、最小绝对误差等。
矩阵的L2范数为矩阵的各个元素平方之和再开平方，又被称为F范数(Frobenius Norm)，欧式距离就是一种L2范数。
矩阵的正无穷范数即是所有元素绝对值的最大值，负无穷范数即是所有元素绝对值的最小值。

这里简单再介绍一下Eigen中的“广播”,通过colwise()、rowwise()函数即可实现。广播是在两个大小不同的矩阵和向量上进行的(不能是两个矩阵)，将向量在矩阵上进行重复进行运算，通过例子看会比较直观。

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    MatrixXd m1(2, 4);
    m1 << 1, 2, 3, 4, 5, 6, 7, 8;
    Vector2d m2;
    m2 << 1, 2;
    MatrixXd m3 = m1.colwise() + m2;
    cout << m1 << endl;
    cout << m3 << endl;
    return 0;
}

最终结果如下。

6.Eigen中的Array

(1)加减乘除

相比于Matrix面向线性代数而设计，Array是Eigen中一个特别的类型，其设计的初衷是面向“元素级”运算(coefficient-wise operation)，具有更一般的用途。例如两个相同大小矩阵间元素级的乘法(相同位置元素相乘并放在对应位置)。其创建、初始化等操作均与Matrix相同，不同的是关键词换成Array，Eigen也提供了预定义好的类型。但与Matrix稍有不同的是，形如ArrayXd表示的并不是X×X的矩阵，而是长度为X的1维数组；对于2维Array表示为ArrayXXd。文档里说是为了和习惯一致(We adopt the convention that typedefs of the form ArrayNt stand for 1-dimensional arrays, where N and t are the size and the scalar type.)。

Array乘法示例如下：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    Array22d a1;
    a1 << 1, 2, 3, 4;
    Array22d a2;
    a2 << 3, 2, 1, 0;
    cout << a1 * a2 << endl;
    return 0;
}

(2)其它操作

arr.abs()：逐元素取绝对值
arr.sqrt()：逐元素开根号
arr.pow()：逐元素乘方
arr1.min(arr2)：将两个Array中相应位置的最小值组成一个新Array
arr1.max(arr2)：将两个Array中相应位置的最大值组成一个新Array

(3)与Matrix相互转换

可以看到Array在元素级运算上有着强大的优势，其本身也可以与Matrix相互转换，也十分简单。将Matrix转换为Array函数为mat.array()，将Array转换为Matrix函数为arr.matrix()，这样的转换不用担心会有运行时性能的损耗。但需要注意的是Eigen是不允许Matrix和Array混合运算的。

事实上，由于元素级运算在矩阵中很常见，所以Eigen对于Matrix其实内置了一些函数，均以cwise开头，如mat.cwiseProduct()对应元素相乘、mat.cwiseAbs()元素取绝对值、mat.cwiseSqrt()逐元素开根号、mat.cwiseMin()将两个矩阵中相应位置的最小值组成一个新矩阵等等，更多函数可以查看官方文档。

下面是一个Array与Matrix互转的示例：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    MatrixXd m1(3, 2);
    m1 << 4, 5, 8, 3, 5, 0;
    cout << (m1.array() - 1.2).matrix() << endl;
    return 0;
}

短短几行代码就实现了将矩阵每个元素都减去同一个数，比之前的版本要简洁很多。因此善用Array可以简化代码与计算。

7.Eigen中的矩阵块操作

(1)常规操作

说到矩阵的块操作，熟悉Python的同学应该都非常熟悉Numpy中非常好用的切片功能，这就是用来进行块操作的。Eigen作为矩阵运算库同样也具备块操作的能力。在Eigen中有两种方式进行块操作，一种是动态尺寸块(dynamic-size block)：mat.block(i,j,p,q)，另一种是固定尺寸块(fixed-size block)：mat.block<p,q>(i,j)。它们在语义上等价，都表示从矩阵的i行j列开始取大小为p行q列的块，注意p行q列是从第i行j列开始算的。唯一的区别就是如果你的矩阵比较小(固定大小矩阵)，固定尺寸块会有更高的效率。在获得了矩阵块之后即可对其进行修改等一系列操作。示例代码如下：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    MatrixXd m = MatrixXd::Random(5, 5);
    cout << m << endl << endl;
    cout << m.block(1, 1, 2, 2) << endl << endl;
    cout << m.block<1, 2>(2, 2) << endl;
    return 0;
}

(2)其它特殊操作

mat.row()：用于单独取出某一行(可修改)
mat.col()：用于单独取出某一列(可修改)
mat.topLeftCorner()：用于取出左上角元素

更多函数参考官方文档。

8.Eigen中的Map

Map类主要是用来处理C++中原生的数组的，这样就可以将其转化为Eigen中的矩阵或向量进行操作了。它也可以用在对矩阵修改大小、切片等操作中。新建Map对象的模板参数如下：

Map<Matrix<typename Scalar, int RowsAtCompileTime, int ColsAtCompileTime> >

需要3个模板参数分别是数据类型、行数、列数。而如果采用预定义类型，则直接传入即可，不需要模板参数了。此外Map的构造函数中还需要两个其它参数：指向数据的指针以及修改后矩阵的大小。例如如下新建Map的代码：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    double data[8];
    for (int i = 0; i < 8; ++i) {
        data[i] = i;
    }
    Map<MatrixXd> md1(data, 2, 4);
    Map<Matrix2d> md2(data);
    Map<Matrix<double, 4, 2>> md3(data);
    Map<Matrix<double, 4, 2, RowMajor>> md4(data);
    cout << md1 << endl << endl;
    cout << md2 << endl << endl;
    cout << md3 << endl << endl;
    cout << md4 << endl;
    return 0;
}

需要注意的是Map构造默认是按照列优先的，即按照列依次从上倒下、从左到右填充，若想换成行优先只需要在模板参数里加上RowMajor即可。

9.其它操作

(1)Reshape

注意区别矩阵的Reshape和Resize，两者是不一样的。Reshape是指不改变矩阵元素个数的情况下，改变矩阵中元素的大小，简单例子如转置，2x3->3x2。而Resize则是改变矩阵元素个数情况下，改变矩阵的大小规模，如2x3->4x4。Resize前面说过了可以用resize()和conservativeResize()。而Reshape即可以用Map。

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    MatrixXf M1(3, 3);    // Column-major storage
    M1 << 1, 2, 3,
            4, 5, 6,
            7, 8, 9;
    Map<RowVectorXf> v1(M1.data(), M1.size());
    cout << "v1:" << endl << v1 << endl;
    return 0;
}

(2)Slicing切片

所谓切片就是抽取矩阵中指定的一组行、列或一些元素。直接看代码：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    RowVectorXf v = RowVectorXf::LinSpaced(20, 0, 19);
    cout << "Input:" << endl << v << endl;
    Map<RowVectorXf, 0, InnerStride<2> > v2(v.data(), v.size() / 2);
    cout << "Even:" << v2 << endl;
    return 0;
}

(3)Eigen与OpenCV的数据类型转换

OpenCV中的Mat是可以和Eigen的Matrix比较方便的转换的，下面进行介绍。使用OpenCV首先要配置CMake，和Eigen类似，如下：

cmake_minimum_required(VERSION 3.12)
project(eigenLearn)

set(CMAKE_CXX_STANDARD 11)

find_package(Eigen3 REQUIRED)
include_directories(${EIGEN3_INCLUDE_DIRS})

find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})

add_executable(eigenLearn main.cpp)
target_link_libraries(${PROJECT_NAME} ${OpenCV_LIBS})

对于include_directories，OpenCV的写法不像Eigen那样固定，写成OPENCV、opencv、OpenCV甚至是opencV都可以，对大小写不敏感。与Eigen不同的是OpenCV需要target_link_libraries，且target_link_libraries则必须要写成OpenCV，否则会报错(找不到lib，报未定义的引用错误)。

然后就是写代码了，在OpenCV中提供了与Eigen进行数据转换的函数，在opencv2/core/eigen.hpp头文件里，因此需要在文件中引入。同时还需要引入opencv2/opencv.hpp文件，其中包含了基础的imread()、imshow()等函数。转换代码如下：

#include <iostream>
#include <Eigen/Dense>
#include <opencv2/opencv.hpp>
#include <opencv2/core/eigen.hpp>


using namespace std;
using namespace Eigen;
using namespace cv;

int main() {
    Mat img = imread("../img.jpg", IMREAD_GRAYSCALE);   // 载入图像
    MatrixXi matrix(img.rows, img.cols);    // 新建一个int类型的Eigen矩阵

    cv2eigen(img, matrix);  // 调用函数将Mat转成Matrix

    matrix.block(100, 100, 5, 10) = MatrixXi::Constant(5, 10, 255); // 对转换后的图像进行简单修改

    Mat modi_img;   // 新建一个Mat对象
    eigen2cv(matrix, modi_img); // 将Matrix转回Mat
    return 0;
}

关于OpenCV特有的Mat类型，之后有时间单独写篇博客介绍，也不是本篇博客的重点。

以上便是Eigen库中与矩阵相关的基础内容了，之后再介绍解方程、矩阵分解、几何等其它模块。最后官方也提供了一个API快速查找指南，点击查看，可以很方便地找到对应函数。

10.参考资料

[1]http://eigen.tuxfamily.org/dox/GettingStarted.html
[2]http://eigen.tuxfamily.org/dox/group__TutorialMatrixClass.html
[3]http://eigen.tuxfamily.org/dox/group__TutorialMatrixArithmetic.html
[4]http://eigen.tuxfamily.org/dox/group__TutorialArrayClass.html
[5]http://eigen.tuxfamily.org/dox/group__TutorialAdvancedInitialization.html
[6]http://eigen.tuxfamily.org/dox/group__TutorialReductionsVisitorsBroadcasting.html
[7]http://eigen.tuxfamily.org/dox/group__TutorialMapClass.html
[8]http://eigen.tuxfamily.org/dox/group__TutorialReshapeSlicing.html
[9]http://eigen.tuxfamily.org/dox/group__TopicStorageOrders.html
[10]https://blog.csdn.net/a493823882/article/details/80569888
[11]https://blog.csdn.net/zaishuiyifangxym/article/details/81673491
[12]https://blog.csdn.net/weixin_42587961/article/details/94446580
[13]https://www.e-learn.cn/content/qita/781840
[14]http://eigen.tuxfamily.org/dox/group__QuickRefPage.html

Menu

Eigen学习与使用笔记1

Aug 21,2019 14158 words 51 min

1.库的安装

2.CMake中库的声明与使用

3.代码中头文件引用与简单示例

4.Eigen中的矩阵与向量

(1)创建

(2)初始化

(3)矩阵元素操作与矩阵大小获取

(4)小技巧

5.Eigen中的矩阵运算

(1)加减乘除

(2)矩阵本身运算

6.Eigen中的Array

(1)加减乘除

(2)其它操作

(3)与Matrix相互转换

7.Eigen中的矩阵块操作

(1)常规操作

(2)其它特殊操作

8.Eigen中的Map

9.其它操作

(1)Reshape

(2)Slicing切片

(3)Eigen与OpenCV的数据类型转换

10.参考资料