Eigen学习与使用笔记2

1.求解线性方程组
2.计算特征值与特征向量
3.线性方程组的最小二乘解
4.矩阵分解
参考资料

上一篇笔记介绍了Eigen中矩阵相关的基本操作，这次介绍与学习Eigen中与线代有关的模块与函数，具体为求解线性方程组和矩阵分解两块。

1.求解线性方程组

线代中形如Ax=b的线性方程组是最简单的入门示例。对于常规适定的线性方程组(未知数个数=方程个数)，可以采用常规的矩阵分解法求解。在Eigen中有多种解法可供选择，以满足在精度与效率上不同的需求。有如下方程组：

\[\left\{\begin{matrix} 1x_{1}+2x_{2}+3x_{3}=3\\ 4x_{1}+5x_{2}+6x_{3}=3\\ 7x_{1}+8x_{2}+10x_{3}=4 \end{matrix}\right.\]

解方程组的示例代码如下：

# include<iostream>
# include<Eigen\Dense>

using namespace std;
using namespace Eigen;

int main(){
	Matrix3f A;
	Vector3f b;
	A << 1, 2, 3, 4, 5, 6, 7, 8, 10;
	b << 3, 3, 4;
	Vector3f x;
	x = A.colPivHouseholderQr().solve(b);
	cout << x << endl;
	system("pause");
	return 0;
}

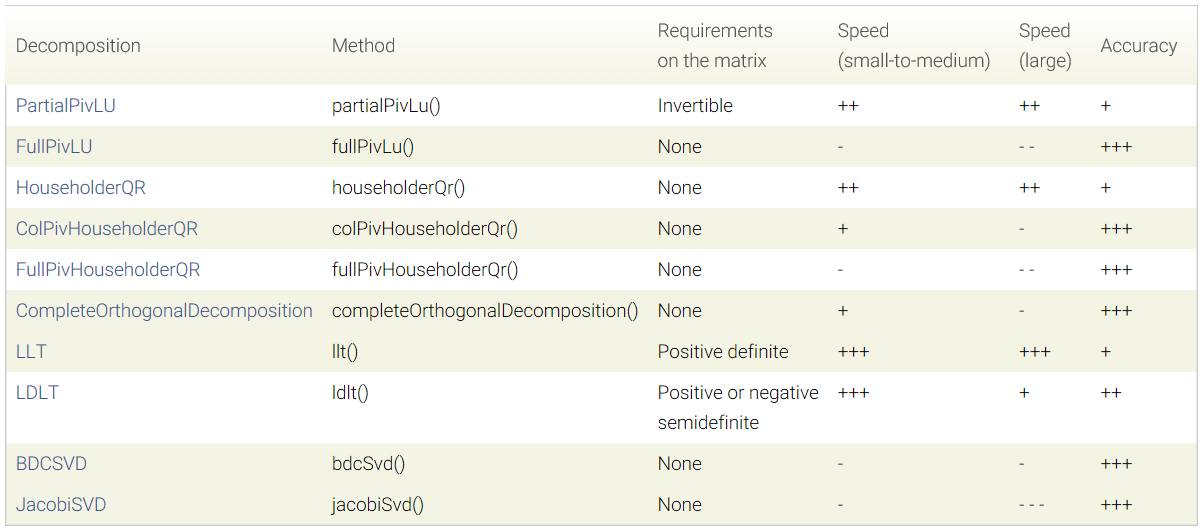
上述代码调用了.colPivHouseholderQr()函数对方程进行求解。Eigen中所有不同方法调用都有固定的格式：x = A.methodName().solve(b)，如下是Eigen中一些常用方法的比较，根据需要选择不同方法。其中Eigen的LLT对应Cholesky分解方法。当然，Eigen还可以解一些长的比较“奇怪”的方程组(如x、b并不是向量而是矩阵)，如下方程组：

\[\begin{pmatrix} 2 & -1\\ -1 & 3 \end{pmatrix}\begin{pmatrix} x_{1} & x_{2}\\ x_{3} & x_{4} \end{pmatrix}=\begin{pmatrix} 1 & 2\\ 3 & 1 \end{pmatrix}\]

求解代码如下：

# include<iostream>
# include<Eigen\Dense>

using namespace std;
using namespace Eigen;

int main(){
	Matrix2f A, b;
	A << 2, -1, -1, 3;
	b << 1, 2, 3, 1;
	Matrix2f x = A.ldlt().solve(b);
	cout << x << endl;
	system("pause");
	return 0;
}

如果对上面方程组展开重新合并，就变成如下常规的Ax=b形式了，可以看出依然是适定方程组。

\[\begin{pmatrix} 2 & 0 & -1 & 0\\ 0 & 2 & 0 & -1\\ -1 & 0 & 3 & 0\\ 0 & -1 & 0 & 3 \end{pmatrix}\begin{pmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{pmatrix}=\begin{pmatrix} 1\\ 2\\ 3\\ 1 \end{pmatrix}\]

2.计算特征值与特征向量

Eigen中计算特征值与特征向量非常简单，构造一个EigenSolver，然后分别调用其成员函数.eigenvalues()、.eigenvectors()即可获得特征值与特征向量。在Eigen中提供了多种Solver，可查阅文档。直接看代码：

# include<iostream>
# include<Eigen\Dense>

using namespace std;
using namespace Eigen;

int main(){
	Matrix2f A;
	A << 1, 2, 2, 3;
	EigenSolver<Matrix2f> eigensolver(A);
	if (eigensolver.info() == Success){
		cout << eigensolver.eigenvalues() << endl;
		cout << eigensolver.eigenvectors() << endl;
	}
	else{
		cout << "error while solving...";
	}
	system("pause");
	return 0;
}

在上面的代码中通过.info()函数查询了求解状态，如果成功继续，否则输出错误。

3.线性方程组的最小二乘解

前面说了，如果一个线性方程组是适定的(未知数个数=方程个数)，采用常规的矩阵分解方法即可得到解。对正定方程组采用最小二乘法和矩阵分解法得到的结果相同。而如果一个线性方程组是超定的(overdeterminated，未知数个数>方程数)，这时候常规方法无解，就需要用最小二乘拟合最优结果。

(1)SVD方法

求解最小二乘最精确的解法文档中说是SVD分解。Eigen中提供了多种解法，官方推荐的是BDCSVD方法。下面直接看SVD方法使用示例，有如下超定方程组：

\[\left\{\begin{matrix} 1x_{1}+2x_{2}=3\\ 5x_{1}-3x_{2}=7\\ 7x_{1}+10x_{2}=1 \end{matrix}\right.\]

最小二乘求解代码如下：

# include<iostream>
# include<Eigen\Dense>

using namespace std;
using namespace Eigen;

int main(){
	MatrixXf A(3, 2);
	Vector3f b;
	Vector2f x;
	A << 1, 2, 5, -3, 7, 10;
	b << 3, 7, 1;
	x = A.bdcSvd(ComputeThinU | ComputeThinV).solve(b);
	cout << x << endl;
	system("pause");
	return 0;
}

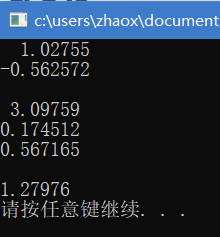
可以得到解为：

\[\left\{\begin{matrix} x_{1}=1.02755\\ x_{2}=-0.56257 \end{matrix}\right.\]

这样得到的x就是通过最小二乘算出来的。这里.bcdScd()函数里面的参数ComputeThinU | ComputeThinV必须要写(可以先记住)，否则会报错，关于参数的解释放在矩阵分解部分介绍，这里不多说。

如果你比较细心，将得到的解带回方程会发现其并不是严格成立的，有时可能还会相差较大。这是因为对于超定方程，采用最小二乘法得出的解并不一定对每一个方程都严格成立，其确保的是当前解在所有方程上的总误差最小。得到解以后我们可以反算出其解的整体精度，像这样：

# include<iostream>
# include<Eigen\Dense>

using namespace std;
using namespace Eigen;

int main(){
	MatrixXf A(3, 2);
	Vector3f b;
	Vector2f x;
	Vector3f error;
	double mean_error;
	A << 1, 2, 5, -3, 7, 10;
	b << 3, 7, 1;
	x = A.bdcSvd(ComputeThinU | ComputeThinV).solve(b);
	cout << x << endl << endl;
	error = (A*x - b).cwiseAbs();
	mean_error = error.mean();
	cout << error << endl << endl;
	cout << mean_error << endl;
	system("pause");
	return 0;
}

输出结果如下：

可以看到第一个方程误差较大，后面两个还行，平均误差1点几。当然这并不是说最小二乘不行，因为这个方程组是我自己随便造的，所以拟合误差不会小，真实数据会好很多。

除了SVD方法，QR分解方法、正规方程法(normal equation)等，下面逐一演示用法。

(2)QR方法

QR分解方法：

# include<iostream>
# include<Eigen\Dense>

using namespace std;
using namespace Eigen;

int main(){
	MatrixXf A(3, 2);
	Vector3f b;
	Vector2f x;
	A << 1, 2, 5, -3, 7, 10;
	b << 3, 7, 1;
	x = A.colPivHouseholderQr().solve(b);
	cout << x << endl << endl;
	system("pause");
	return 0;
}

(3)正规方程法

正规方程法。所谓正规方程法思想是若要求解Ax=b，等价于方程两边同乘A的转置：ATAx=ATb，这样系数矩阵可化为方阵。代码如下：

# include<iostream>
# include<Eigen\Dense>

using namespace std;
using namespace Eigen;

int main(){
	MatrixXf A(3, 2);
	Vector3f b;
	Vector2f x;
	A << 1, 2, 5, -3, 7, 10;
	b << 3, 7, 1;
	x = (A.transpose()*A).ldlt().solve(A.transpose()*b);
	cout << x << endl << endl;
	system("pause");
	return 0;
}

需要注意的是如果系数矩阵A本身是病态的，采用正规方程法不是一个很好的选择。所谓病态矩阵是指矩阵A的行列式乘以A逆的行列式的结果，记为K，若这个值很大即为病态。

以上主要介绍了SVD、QR、正规方程三种方法求解线性最小二乘问题。其中SVD精度最高、速度最慢，正规方程法精度最低、速度最快，QR方法则介于二者之间。

4.矩阵分解

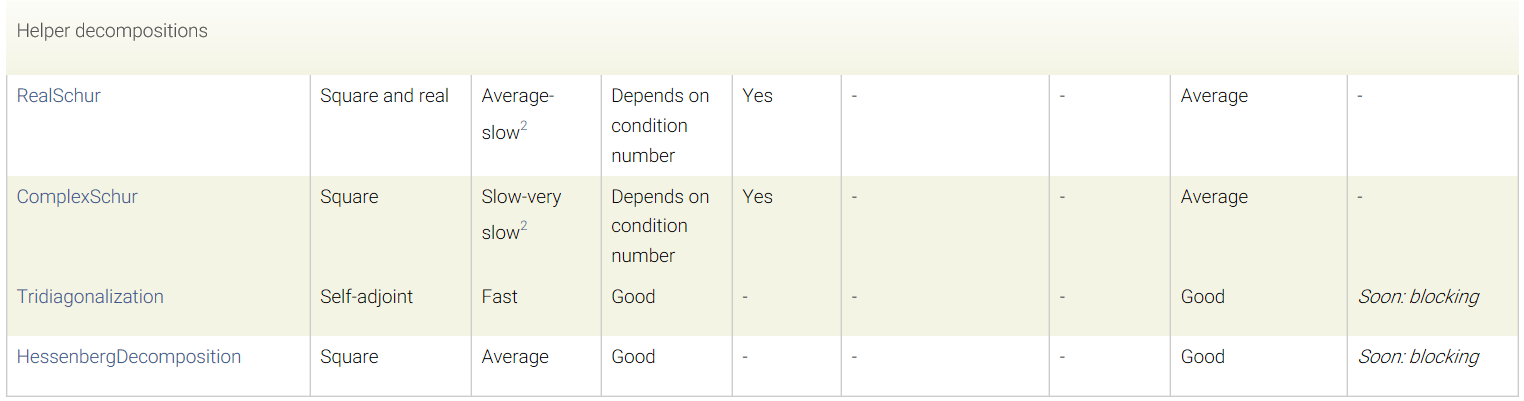
官方文档中关于矩阵分解的方法对比见这里，这里也简单贴一下。

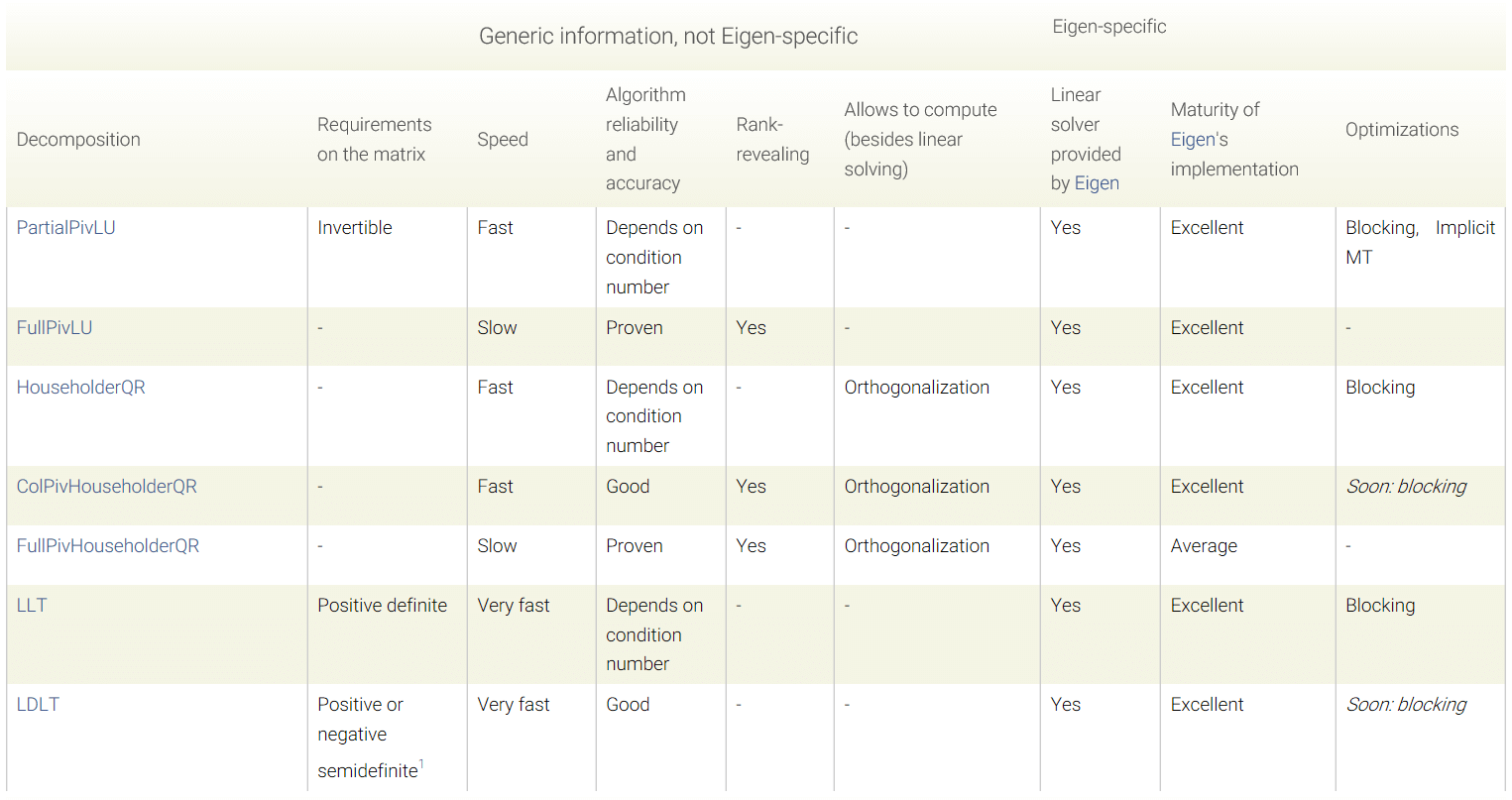
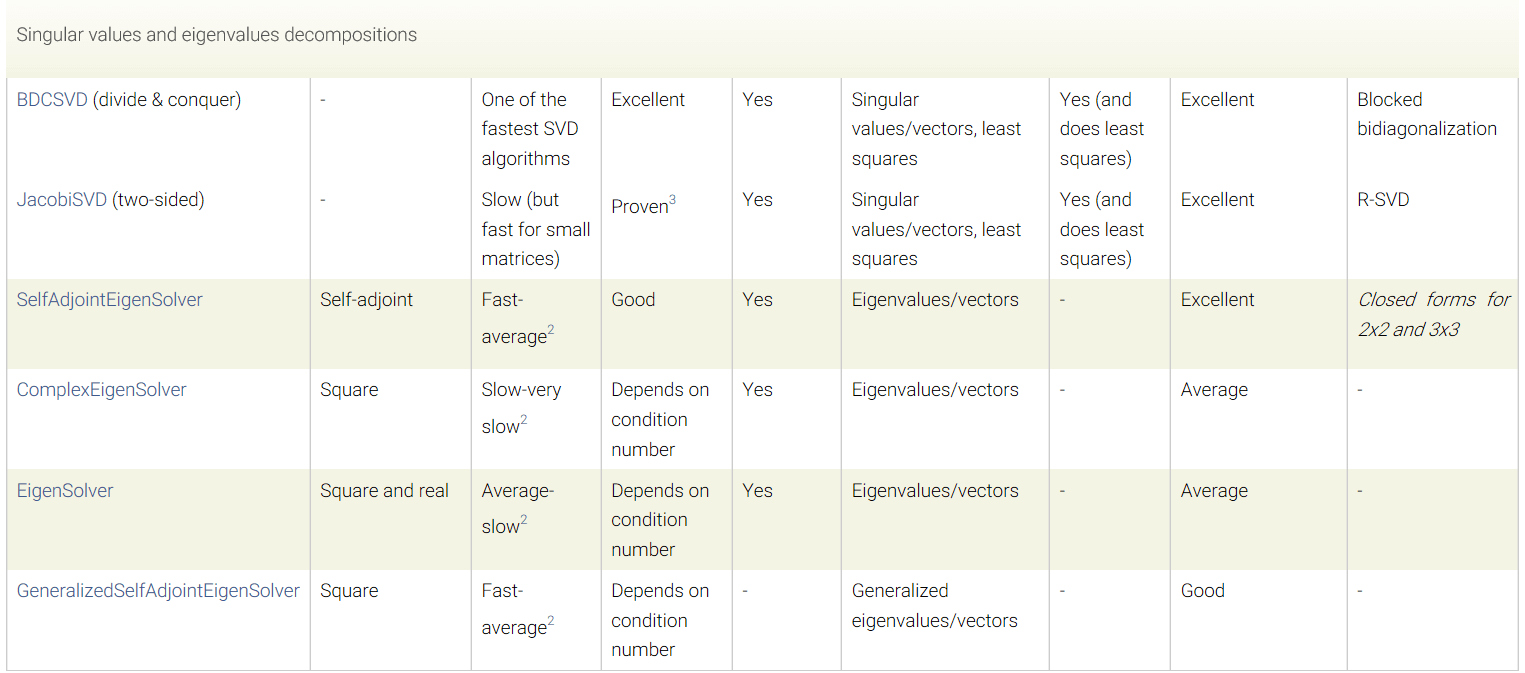
这里简单补充一下常见矩阵分解的定义与算法。

(1)LU三角分解

三角分解法是仅对方阵有效，将原方阵分解成一个上三角形矩阵或是排列(permuted)的上三角形矩阵和一个下三角形矩阵，这样的分解法又称为LU分解法。它的用途主要在简化一个大矩阵的行列式值的计算过程、求反矩阵和求解联立方程组。不过要注意这种分解法所得到的上下三角形矩阵并非唯一，还可找到数个不同的一对上下三角形矩阵，此两三角形矩阵相乘也会得到原矩阵。[L,U]=lu(A)

(2)QR分解

QR分解法对象不一定是方阵，其将矩阵分解成一个正规正交矩阵与上三角形矩阵,所以称为QR分解法,与此正规正交矩阵的通用符号Q有关。[Q,R]=qr(A)

(3)SVD分解

奇异值分解(singular value decomposition,SVD)是另一种正交矩阵分解法；SVD是最可靠的分解法，但是它比QR分解法要花上近十倍的计算时间。[U,S,V]=svd(A)，其中U和V分别代表两个正交矩阵，而S代表一对角矩阵。和QR分解法相同，原矩阵A不必为方阵。使用SVD分解法的用途是解最小平方误差法和数据压缩。

(4)LLT分解

又称Cholesky分解，其把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。它要求矩阵为方阵，且所有特征值必须大于零，故分解的下三角的对角元也是大于零的(LU三角分解法的变形)。A=LL^T

(5)LDLT分解

LDLT分解法实际上是Cholesky分解法的改进，因为Cholesky分解法虽然不需要选主元，但其运算过程中涉及到开方问题，而LDLT分解法则避免了这一问题，可用于求解线性方程组。也需要分解对象为方阵，分解结果为A=LDL^T。其中L为一下三角形单位矩阵(即主对角线元素皆为1)，D为一对角矩阵(只在主对角线上有元素，其余皆为零)，L^T为L的转置矩阵。

参考资料

[1]http://eigen.tuxfamily.org/dox/group__TutorialLinearAlgebra.html
[2]http://eigen.tuxfamily.org/dox/group__TopicLinearAlgebraDecompositions.html
[3]http://eigen.tuxfamily.org/dox/group__LeastSquares.html
[4]https://www.yuanmas.com/info/8VaPowvBzr.html

Menu