图像二维熵计算的C++实现

1.自定义数据结构体
2.重复元素个数统计
- (1)常规方法
- (2)自己的方法
  - 原理
  - 注意事项
3.性能比较
4.参考资料

在之前这篇博客中详细介绍了图像二维熵的原理与实现代码。但如果跑过代码都应该知道最初的原始代码运算效率很低，一个1080p的影像都需要跑几十秒。不过也一直在进行着优化：从一开始的手写循环统计重复元素个数到用Counter模块，从串行到用multiprocessing模块并行，再到用numba模块并行。效率也在慢慢提高，1080p影像从5.418s到0.845s，有了巨大的提升(剧透一下，用C++重写之后可以降到0.374s)。

在不引入更多加速库的情况下(如CUDA)基本做到了Python的最好水平。但这里的“最好”是对Python而言，而且它在效率方面也并没有什么优势。最适合提升效率的是C++，所以抽了些时间用C++重写了图像二维熵的计算，相比于Python效率有比较大的提升(文末有对比)。本文主要记录用C++重写过程中遇到的一些问题、注意事项以及新的东西。对应Github项目点击查看。

1.自定义数据结构体

整个改写都是基于entropy2dSpeedUp.py进行。而转到C++第一个要做的事情就是自定义数据结构。在Python中CalcIJ()函数返回的是一个包含中央灰度与平均灰度两个元素的元组，但在C++中并没有适合的现成数据类型，所以需要自定义。比较方便的做法是自定义一个结构体就行了，不需要单独写个类。这里定义了IJpair结构体，定义代码如下：

struct IJpair {
    // 自定义IJpair数据格式用于存放数值对
    // 同时重载了==和<使其可以进行大小比较

    int center_p;
    int mean_p;

    bool operator==(const IJpair &ij) const {
        return center_p == ij.center_p && mean_p == ij.mean_p;
    }

    // 比较大小的规则是center_p小的在前，center_p相同时mean_p小的在前
    bool operator<(const IJpair &ij) const {
        if (center_p < ij.center_p) {
            return true;
        } else if (center_p == ij.center_p) {
            if (mean_p < ij.mean_p) {
                return true;
            } else {
                return false;
            }
        } else {
            return false;
        }
    }
};

2.重复元素个数统计

得益于OpenCV中相关API的一致性和C++11标准的新特性，相关函数改写起来难度不大，内容基本相同。这里主要说一个比较麻烦的问题。在统计重复元素个数的时候，Python中采用的是Counter模块做的，但在C++中并没有相关非常类似的模块。虽然在STL中也有count()函数可用，但在本场景下效果并不是很理想。本部分主要介绍两种方式：一种是常规的count()方法，另一种是自己想的算法。

(1)常规方法

常规方法思想很简单，在获得了一组带有重复元素的vector1后，首先将其中的重复元素去掉，只保留非重复元素，将其保存为vector2。依次将vector2中的元素与vector1中的所有元素比较，累计并统计相同个数存放到vector3中，即可得到重复个数。利用vector3即可计算出现概率。上面也说了，由于涉及的是自定义数据类型的大小比较、排序等，因此需要在结构体中按照自己定义的规则重载==和<运算符。如果是一般数据类型，则不需要这么麻烦了。同时由于用到了STL提供的一些算法，因此需要在头文件中包含algorithm文件。示例代码如下：

#include <iostream>
#include <algorithm>

using namespace std;


struct IJpair {
    // 自定义IJpair数据格式用于存放数值对
    // 同时重载了==和<使其可以进行大小比较

    int center_p;
    int mean_p;

    bool operator==(const IJpair &ij) const {
        return center_p == ij.center_p && mean_p == ij.mean_p;
    }

    // 比较大小的规则是center_p小的在前，center_p相同时mean_p小的在前，如(1,2)<(1,3)<(2,1)
    bool operator<(const IJpair &ij) const {
        if (center_p < ij.center_p) {
            return true;
        } else if (center_p == ij.center_p) {
            if (mean_p < ij.mean_p) {
                return true;
            } else {
                return false;
            }
        } else {
            return false;
        }
    }
};


int main() {
    vector<IJpair> IJs;
    IJs.push_back(IJpair{5, 2});
    IJs.push_back(IJpair{3, 2});
    IJs.push_back(IJpair{5, 2});
    IJs.push_back(IJpair{7, 6});
    IJs.push_back(IJpair{3, 2});
    IJs.push_back(IJpair{6, 4});
    IJs.push_back(IJpair{1, 3});
    IJs.push_back(IJpair{5, 2});
    IJs.push_back(IJpair{1, 3});
    IJs.push_back(IJpair{2, 9});

    // 首先得到一个不含重复元素的vector - IJ_set
    vector<IJpair> IJ_set = IJs;
    sort(IJ_set.begin(), IJ_set.end());
    IJ_set.erase(unique(IJ_set.begin(), IJ_set.end()), IJ_set.end());

    // 然后将IJ_set中的元素依次在IJs中遍历并统计个数
    vector<int> item_num;
    for (int l = 0; l < IJ_set.size(); ++l) {
        int num = 0;
        num = count(IJs.begin(), IJs.end(), IJ_set[l]);
        item_num.push_back(num);
    }

    // 输出展示
    for (int i = 0; i < item_num.size(); ++i) {
        printf("(%d,%d) %d\n", IJ_set[i].center_p, IJ_set[i].mean_p, item_num[i]);
    }
    return 0;
}

代码运行结果如下：可以看到，实现了我们对重复元素个数统计的需求。此方法在元素个数不多的情况下可用，但在元素个数超多(如几百万)时计算量太大。例如对于一个1200万像素的影像，一个像素计算一个IJpair，包含1200万个IJpair，假设其中不重复的个数有10000个，采用本方法1个非重复元素需要进行1200万次比较，共需要计算1200亿次，计算量十分夸张。所以此方法不适合本场景。

虽然本方法不合适，但在代码中用到了STL中的一些常用的算法函数，还是值得学习一下的。主要用到sort()、unique()、erase()以及count()函数。相关作用以及用法简单解释如下：

sort():用于对STL容器中的元素进行排序，常规使用格式是sort(vec.begin(),vec.end())，默认是从小到大排序。如果是自定义数据类型排序，记得重载==和<运算符。
unique():用于去除STL容器中的相邻的重复元素，用法是unique(vec.begin(),vec.end())，它会把重复的元素添加到容器末尾(所以容器大小并没有改变)，返回值是去重之后的尾地址。需要注意的是要想用它去重记得先对容器元素排序，使相同元素相邻。
erase():用于擦除内存，有三种调用方式：earse(pos,n)表示从pos开始擦除，擦除n个字符；earse(pos)表示擦除pos后的所有内容；earse(first,last)表示擦除first迭代器和last迭代器之间的内容。在上面的代码中便配合unique()函数实现了去除重复元素。
count():用于统计容器中指定元素的出现次数，用法是count(vec.begin(),vec.end(),item)。与之类似的还有count_if()函数，顾名思义是统计容易中满足某个条件的元素个数。

(2)自己的方法

看了常规方法后，可以发现常规方法的主要问题就在于每一个非重复元素都需要遍历一整遍vector，数量越多越慢。因此思考是否可以找到一种只遍历一次的方法，答案是肯定的。先上代码：

#include <iostream>
#include <algorithm>

using namespace std;


struct IJpair {
    // 自定义IJpair数据格式用于存放数值对
    // 同时重载了==和<使其可以进行大小比较

    int center_p;
    int mean_p;

    bool operator==(const IJpair &ij) const {
        return center_p == ij.center_p && mean_p == ij.mean_p;
    }

    // 比较大小的规则是center_p小的在前，center_p相同时mean_p小的在前，如{1,2}<{1,3}<{2,1}
    bool operator<(const IJpair &ij) const {
        if (center_p < ij.center_p) {
            return true;
        } else if (center_p == ij.center_p) {
            if (mean_p < ij.mean_p) {
                return true;
            } else {
                return false;
            }
        } else {
            return false;
        }
    }
};


int main() {
    vector<IJpair> IJs;
    IJs.push_back(IJpair{5, 2});
    IJs.push_back(IJpair{3, 2});
    IJs.push_back(IJpair{5, 2});
    IJs.push_back(IJpair{7, 6});
    IJs.push_back(IJpair{3, 2});
    IJs.push_back(IJpair{6, 4});
    IJs.push_back(IJpair{1, 3});
    IJs.push_back(IJpair{5, 2});
    IJs.push_back(IJpair{1, 3});
    IJs.push_back(IJpair{2, 9});

    // 第一步，相邻元素两两比较得到结果串
    sort(IJs.begin(), IJs.end());
    vector<int> times;
    times.push_back(0);
    for (int i = 0; i < IJs.size() - 1; ++i) {
        if (IJs[i] == IJs[i + 1]) {
            times.push_back(1);
        } else {
            times.push_back(0);
        }
    }

    // 第二步，统计结果串中非零元素个数并求和
    vector<int> times2;
    int sum = 0;
    for (int j = 0; j < times.size() - 1; ++j) {
        if (times[j] == 0 and times[j + 1] == 0) {
            times2.push_back(times[j] + 1);
        } else if (times[j] == 1 and times[j + 1] == 0) {
            times2.push_back(sum + 1);
            sum = 0;
        } else {
            sum += 1;
            if (j == times.size() - 2) {
                times2.push_back(sum + 1);
            }
        }
    }
    if (times[-1] == 0) {
        times2.push_back(1);
    }

    // 得到不重复元素列表用于显示
    vector<IJpair> IJ_set = IJs;
    sort(IJ_set.begin(), IJ_set.end());
    IJ_set.erase(unique(IJ_set.begin(), IJ_set.end()), IJ_set.end());
    for (int i = 0; i < times2.size(); ++i) {
        printf("(%d,%d) %d\n", IJ_set[i].center_p, IJ_set[i].mean_p, times2[i]);
    }
    return 0;
}

运行结果如下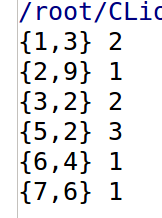：和常规方法是一样的。在实际代码中，将其包装成了函数方便调用。相关原理与注意事项解释如下。

原理

为了阐述方便，这里就使用int类型的数据进行说明。其它类型以及自定义数据类型，只要重载好==和<都是一样的。有数字串如下图所示。

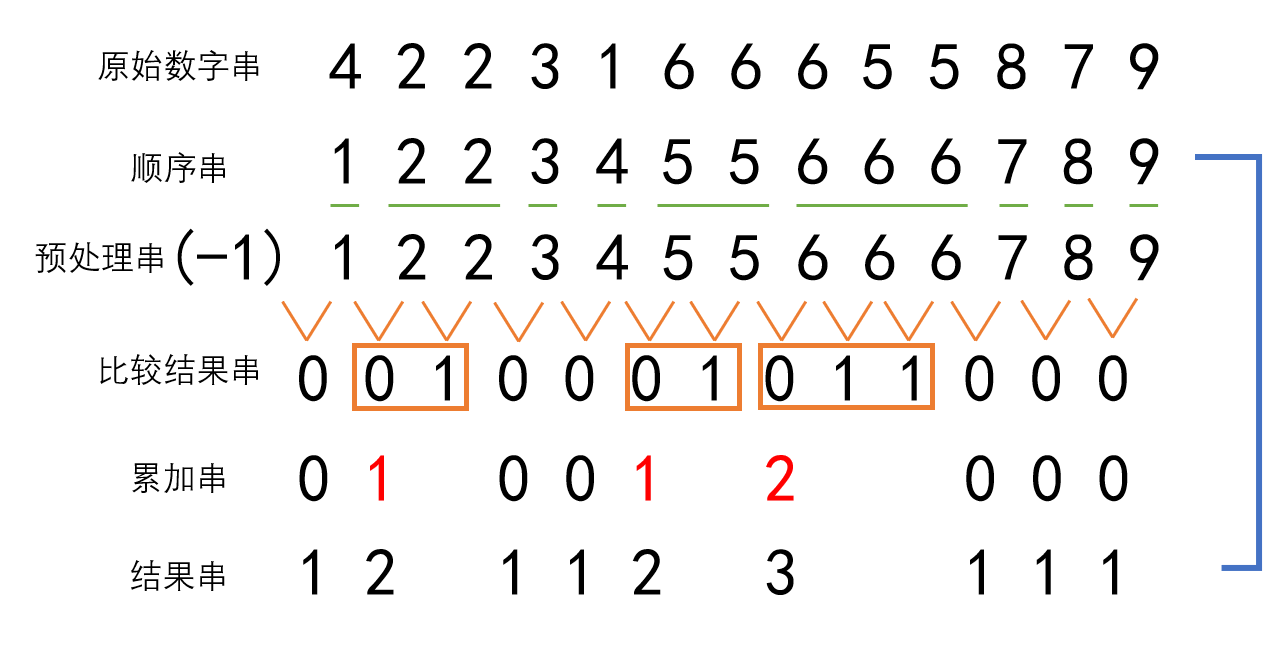
上图中第一行为原始数字串。后续算法对于数字串的要求是相同数字相邻，因此第一步是对原始数字串进行排序，将相同数字排到一起，得到第二个数字串叫顺序串。第二步是在顺序串前增加一个与第一个数字不等的数，如-1，形成第二个数字串叫预处理串。第三步是对预处理串中的数字两两比较，若相等为1，不相等为0，得到第四个由0、1构成的数字串叫比较结果串。第四步从比较结果串的第一个数字开始统计非零数字个数，规定1前面的一个0属于非零数字块的一部分，得到第四个数字串叫累加串。第五步对累加串整体每个数字全部加1，即可得到最终与顺序串中元素对应的元素个数。

其实仔细分析可以发现，排序在这里起了关键作用，为减少计算量提供了基础。在常规方法中虽然也利用了sort()、unique()和earse()函数实现了功能，但其并没有充分利用排序后数字串的特性，从而导致了大量重复的计算和迭代。而本文算法在对数字串排好序之后，只需要两遍遍历即可获得个数，一遍用于比较、一遍用于累加，计算量与数字串长度成线性关系。

注意事项

在写代码的过程中发现有时使用cout混合输出字符串和数字会有问题，改成printf()就可以了，其控制小数位数的输出格式为%.nlf，n为需要保留的位数。C++中可以使用clock()函数用于计时，将两个时刻数值相减最后除以CLOCKS_PER_SEC即可，得到的是以秒为单位的时间。

完整项目代码还是放到了之前的Github项目中，点击查看。

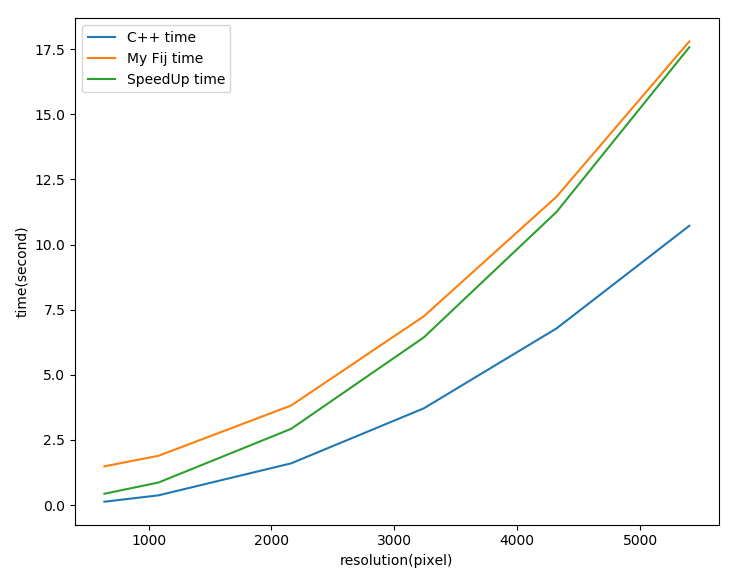
3.性能比较

将C++版本的代码与使用Numba的Python代码进行了耗时比较，完整统计数据在代码drawPlot.py中。根据统计结果绘图如下。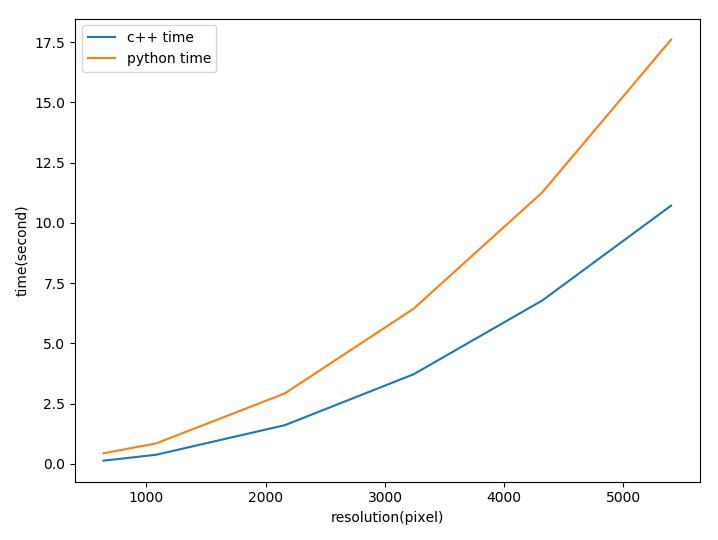可以看出C++的耗时基本是Python的一半。

此外，也将自己的算法用Python实现并和Counter模块进行了比较，比较结果如下。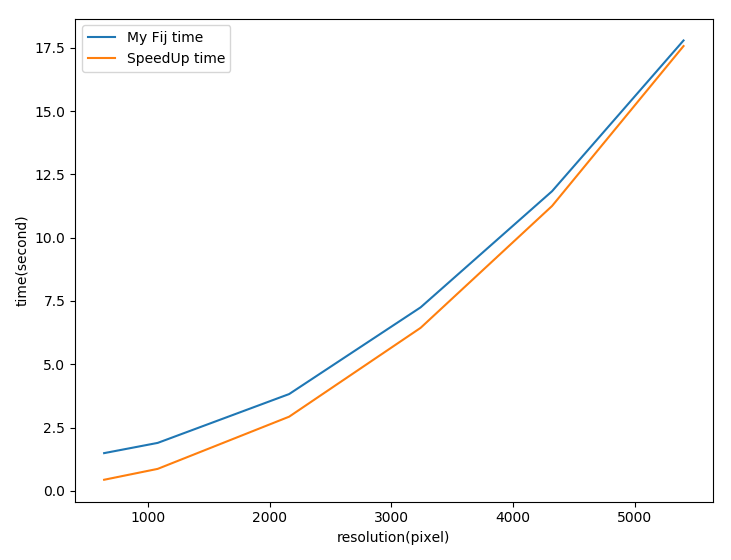可以看到在像素个数较少的情况下，Counter模块的效率会更高一些，但是随着像素数增多，其与自己的算法在效率上越来越接近。

将C++代码、自己实现的Python代码和调用Counter模块的Python代码三者进行比较如下。

4.参考资料

[1]https://www.cnblogs.com/SZxiaochun/p/7732250.html
[2]https://blog.csdn.net/u010141928/article/details/78671603
[3]https://blog.csdn.net/doctor_feng/article/details/11854485
[4]https://www.cnblogs.com/viviancc/p/4135712.html

Menu