Eigen学习与使用笔记3

1.稀疏矩阵创建与初始化
2.稀疏矩阵基本运算
3.解稀疏矩阵方程
4.参考资料

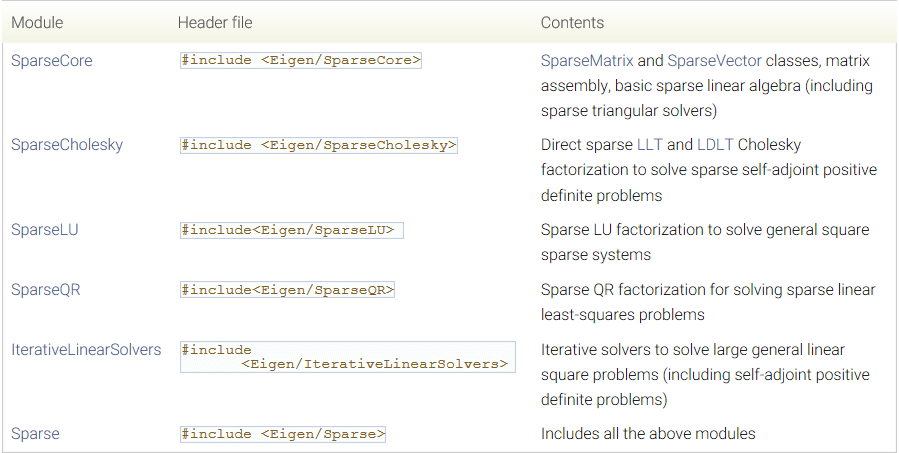
本文主要记录学习Eigen中与稀疏矩阵相关的内容。所谓稀疏矩阵是指大部分元素都为0的矩阵。在许多应用中处理只有少部分元素不为0的大型矩阵时非常常见的情况，因此稀疏矩阵也有一套比较特别的性质和处理方法。与处理稠密矩阵需要包含# include<Eigen\Dense>一样，处理稀疏矩阵同样需要包含相关头文件。在Eigen中与稀疏矩阵有关的头文件如下表所示：据表可知，实际使用时直接# include<Eigen\Sparse>是最方便、也是包含最全的，除非你肯定只会使用具体一种算法。

1.稀疏矩阵创建与初始化

(1)稀疏矩阵创建

Eigen中使用SparseMatrix和SparseVector来表达稀疏矩阵和向量，它需要传入三个模板参数：数据类型(int or double etc.)、储存顺序(RowMajor or ColMajor)以及内部索引类型(int or long etc.)。其中第一个参数是必须的，后面两个参数都有默认值，存储顺序默认为ColMajor，内部索引类型默认为int。而构造函数需要传入的是稀疏矩阵的大小，如果不传入，矩阵大小为0×0，后续可用resize()函数修改。切记不要既没传入大小，后续又没resize()，然后就直接对矩阵赋值，这样是会报错的。以下代码演示了稀疏矩阵的创建：

# include<iostream>
# include<Eigen\Sparse>

using namespace std;
using namespace Eigen;

int main(){
	SparseMatrix<double> m1(100, 50);
	SparseMatrix<int, RowMajor> m2(500, 1000);
	SparseMatrix<float> m3;
	m3.resize(2000, 1000);
	SparseVector<double> vec(1500);
	cout << "m1 row:" << m1.rows() << " col:" << m1.cols() << endl;
	cout << "m2 row:" << m2.rows() << " col:" << m2.cols() << endl;
	cout << "m3 row:" << m3.rows() << " col:" << m3.cols() << endl;
	cout << "vec row:" << vec.rows() << " col:" << vec.cols() << endl;
	system("pause");
	return 0;
}

(2)稀疏矩阵赋值

在创建好后就需要对它进行赋值了。稀疏矩阵并不能像稠密矩阵那样使用逗号赋值语法(comma-initializer)。官方推荐的可以保证良好性能的方法是创建一个元素类型为triplets的列表，然后再将其转换为稀疏矩阵。所谓triplets是Eigen中定义的一种用于储存稀疏矩阵的非零值数据结构，存储格式是(i,j,value)。其包含两个模板参数：数据类型以及储存索引。第二个参数有默认值，因此一般只需要设置第一个参数即可。构造函数常用的是输入三个参数，分别是行、列以及数值。简单使用如下：

# include<iostream>
# include<Eigen\Sparse>

using namespace std;
using namespace Eigen;

int main(){
	Triplet<double> t1(185, 441, 2.6);
	cout << "row " << t1.row() << endl;
	cout << "col " << t1.col() << endl;
	cout << "val " << t1.value() << endl;
	system("pause");
	return 0;
}

代码中分别调用了Triplet对象的成员函数row()获取行数、col()获取列数、value()获取数值。

因此在对稀疏矩阵赋值时，将多个Triplet组成一个列表，调用稀疏矩阵的成员函数setFromTriplets()即可。除了使用Triplet还有一种更加“简单粗暴”的办法，就是调用稀疏矩阵的成员函数.insert()直接插入数值。这样做的好处是可以不用新建Triplet对象和列表，可能会有更高性能、内存占用更少。直接看代码：

# include<iostream>
# include<Eigen\Sparse>

using namespace std;
using namespace Eigen;

int main(){
	vector<Triplet<double>> triplets;
	SparseMatrix<double> sm(100, 100);
	
	// 构造数据
	for (int i = 1; i < 101; i++){
		triplets.push_back(Triplet<double>(i - 1, i - 1, i));
	}

	// 两种不同方式设置数据
	sm.setFromTriplets(triplets.begin(), triplets.end());
	sm.insert(5, 1) = 7;

	cout << sm.block(0, 0, 10, 10) << endl;
	system("pause");
	return 0;
}

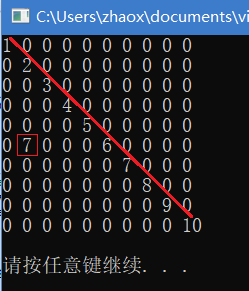
上述代码采用了两种不同方式进行赋值。构造了一个100×100的稀疏矩阵，除了被直接赋值的(5,1)外，只有对角线元素不为0，并且输出了前10行、10列的数据，如下。可以看到圆满完成了赋初值的任务。

(3)稀疏矩阵其它成员函数

.transpose()这种常见的、和稠密矩阵相同的就不说了，一些不一样的函数如下：

.coeffRef(i,j)：用于获得位于i行j列的元素，和.coeff(i,j)效果一样

.makeCompressed()：按照压缩算法将稀疏矩阵压缩

.reserve()：保留空间。例如mat.reserve(VectorXi::Constant(cols,6));表示为每一列保留6个非零元素空间

2.稀疏矩阵基本运算

Eigen中稠密矩阵的大部分运算都可以直接用在稀疏矩阵上，如+、-、×、.cwiseProduct()等。但需要注意的是进行运算的稀疏矩阵的储存顺序必须要一致，否则在编译时就会出错。例如计算A^T+A，A^T必须与A有相同的存储顺序。

# include<iostream>
# include<Eigen\Sparse>

using namespace std;
using namespace Eigen;

int main(){
	SparseMatrix<double> sm1(2, 2);
	sm1.insert(0, 0) = 0;
	sm1.insert(0, 1) = 0;
	sm1.insert(1, 0) = 4;
	sm1.insert(1, 1) = 1;
	cout << sm1 << endl << endl;
	
	SparseMatrix<double> sm2(2, 2);
	sm2.insert(0, 0) = 1;
	sm2.insert(0, 1) = 0;
	sm2.insert(1, 0) = 0;
	sm2.insert(1, 1) = 2;
	cout << sm2 << endl << endl;

	SparseMatrix<double> sm3;
	sm3 = SparseMatrix<double,ColMajor>(sm1.transpose()) + sm2;
	cout << sm3 << endl;

	system("pause");
	return 0;
}

上述代码中如果不修改转置后稀疏矩阵的存储顺序，直接写sm3 = sm1.transpose() + sm2;是会报错的，不信可以试一试。这个限制仅仅针对稀疏矩阵，对于稠密矩阵不需要这样。

其它如块操作等等，与稠密矩阵接口相同，可以直接使用，此处不再赘述。

3.解稀疏矩阵方程

(1)常规稀疏矩阵方程求解

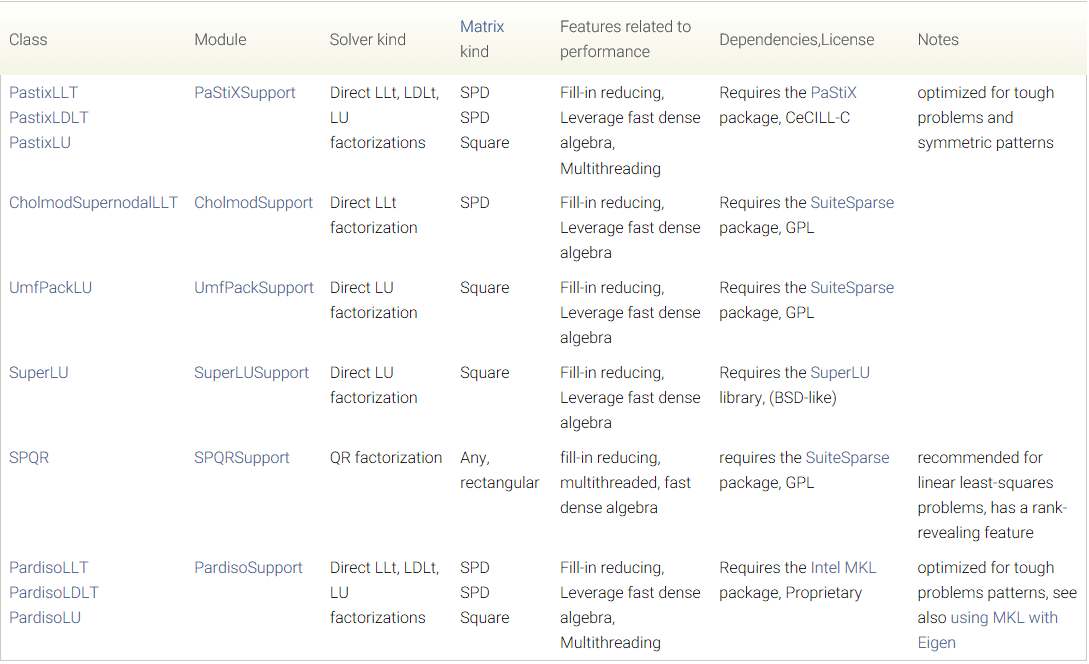
解方程相关内容其实和之前稠密矩阵差不多。这里先贴一张官方文档里的solver的总结以便查阅。

内置的直接求解器内置的迭代求解器外部求解器的包装

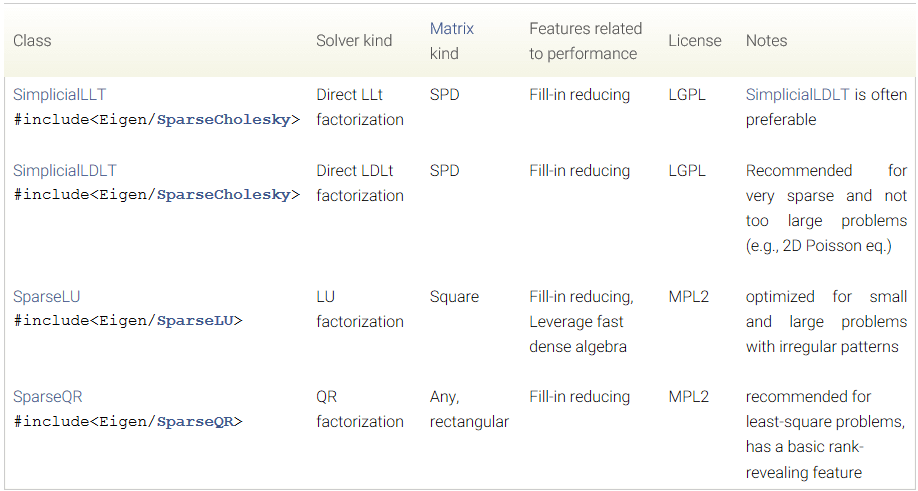
以上所有求解器都有相同的使用方法。先看一下官方给的典型和通用的例子：

#include <Eigen/RequiredModuleName>
// ...
SparseMatrix<double> A;
// fill A
VectorXd b, x;
// fill b
// solve Ax = b
SolverClassName<SparseMatrix<double> > solver;
solver.compute(A);
if(solver.info()!=Success) {
  // decomposition failed
  return;
}
x = solver.solve(b);
if(solver.info()!=Success) {
  // solving failed
  return;
}
// solve for another right hand side:
x1 = solver.solve(b1);

可以看到核心只有两步：compute()和solve()。在构造好求解器solver后，调用solver的compute()函数，传入稀疏矩阵A，然后调用solver的solve()函数，传入等号右边数字b，求解的结果由solve()函数返回。当然如果为了方便还可以将两步写在一行里，更为简洁x = solver.compute(A).solve(b);。

为了加深理解，实际使用示例如下。构造了如下的稀疏矩阵方程。

\[\begin{pmatrix} 2 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 2 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 1\\ 0 & 0 & 1 & 1 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ x_{5}\\ x_{6} \end{pmatrix}=\begin{pmatrix} 2\\ 4\\ 1\\ 5\\ 8\\ 3 \end{pmatrix}\]

代码采用SparseLU方法进行求解，其它方法只需要将名字换一下就行了，十分简单。但也需要注意各方法的特点，有些方法可能不适合本问题，会导致求解出错(如SimplicialLLT方法)或求解的结果不对(如SimplicialLDLT方法)。同时为了突出主要步骤，将判断是否成功的内容去掉了，实际使用过程中最好加上，便于查找问题。

# include<iostream>
# include<Eigen\Sparse>

using namespace std;
using namespace Eigen;

void initMats(SparseMatrix<double> &A, VectorXd &b){
	A.insert(0, 0) = 2;
	A.insert(1, 1) = 1;
	A.insert(1, 2) = 2;
	A.insert(2, 2) = 1;
	A.insert(3, 3) = 1;
	A.insert(3, 5) = 1;
	A.insert(4, 2) = 1;
	A.insert(4, 3) = 1;
	A.insert(4, 4) = 1;
	A.insert(5, 5) = 1;

	b << 2, 4, 1, 5, 8, 3;
}

int main(){
	// 新建矩阵，注意要指定大小
	SparseMatrix<double> A(6,6);
	VectorXd b(6), x;
	
	// 为了代码简洁，将赋值代码单独写成了函数
	initMats(A, b);

	//构建solver
	SparseLU<SparseMatrix<double>> solver;

	// compute步骤
	solver.compute(A);
	// solver步骤
	x = solver.solve(b);

	// 输出结果
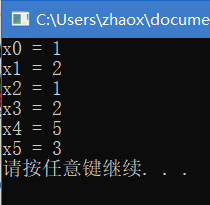
	for (int i = 0; i < x.rows(); i++){
		cout << "x" << i << " = " << x(i) << endl;
	}
	system("pause");
	return 0;
}

求解结果如下：

前面说了需要注意各种方法的特点，在介绍各方法的特点之前先复习几个矩阵论中的概念。

共轭矩阵(Self-adjoint Matrix):共轭矩阵，又称自共轭矩阵。共轭矩阵是矩阵本身先转置再把矩阵中每个元素取共轭得到的矩阵。矩阵中每一个第i行第j列的元素都与第j行第i列的元素的共轭相等。
厄米特矩阵(Hermitian Matrix)：共轭矩阵的一种。在共轭矩阵的基础上，厄米特矩阵要求主对角线上的元素必须为实数。对于只包含实数元素的矩阵(实矩阵)，如果它是对称阵，即所有元素关于主对角线对称，那么它是厄米特矩阵。厄米特矩阵可看作是实对称矩阵的推广。

各类方法特点及其适用的矩阵类型如下：

LLT:用于self-adjoint matrices，SPD(Symmetric Positive Definite)，对称正定矩阵
LDLT:用于general hermitian matrices，SPD(Symmetric Positive Definite)，对称正定矩阵
LU:用于non hermitian matrices，必须为方阵
QR:用于rectangular matrices，任意大小矩阵，适用于最小二乘问题

所以对于代码中的方程组，其并不属于厄米特矩阵，所以LLT和LDLT方法都不能用。从这四个方法也可以看出来，QR方法是最通用的，其次是LU方法，最后是LLT和LDLT方法。

(2)对有相同稀疏模式的多个方程组的求解

此外在Eigen中还提供了一个对于相同稀疏模式(same sparsity pattern)方程组的求解。所谓相同稀疏模式矩阵就是指非零元素位置相同、但数值不同的两个或多个稀疏矩阵。这种情况很常见，对于很多问题，在条件不变的情况下，其方程组的相互约束关系也不变，变的只是数值。在需要多次求解这些矩阵的时候，由于具有相同的稀疏模式，就不需要求一个跑一遍完整步骤。可以按照如下流程求解：

SolverClassName<SparseMatrix<double> > solver;
solver.analyzePattern(A);   // for this step the numerical values of A are not used
solver.factorize(A);
x1 = solver.solve(b1);
x2 = solver.solve(b2);
...
A = ...;                    // modify the values of the nonzeros of A, the nonzeros pattern must stay unchanged
solver.factorize(A);
x1 = solver.solve(b1);
x2 = solver.solve(b2);
...

(3)对compute函数的进一步分析

compute()函数等价于analyzePattern()和factorize()的组合。analyzePattern()用于记录矩阵中的非零元素，这一步只会记录矩阵的结构不会记录具体的数值。所以该函数的结果可以被用在具有相同结构的线性系统的求解中，这在上面的代码中也有提现。factorize()函数会计算矩阵中的系数。

(4)迭代法求解稀疏矩阵方程组

上面介绍的都是直接法求解矩阵方程，下面简单介绍另一种迭代求解方法。整体的求解流程都是一样的，还是compute()+solve()，下面直接上代码。

# include<iostream>
# include<Eigen\Sparse>

using namespace std;
using namespace Eigen;

int main(){
	int n = 1000;
	VectorXd x(n), b(n);
	SparseMatrix<double> A(n, n);
	
	// fill A and b
	ConjugateGradient<SparseMatrix<double>, Lower | Upper> cg;
	cg.compute(A);
	x = cg.solve(b);
	
	cout << "#iterations:	" << cg.iterations() << endl;
	cout << "estimated error:	" << cg.error() << endl;
	
	// update b, and solve again
	x = cg.solve(b);
	system("pause");
	return 0;
}

更多有关迭代法的内容参考这里。

(5)一句话总结

所以一句话总结：稀疏矩阵方程组求解=compute()+solve()，其中compute()=analyzePattern()+factorize()，故稀疏矩阵方程求解也等于analyzePattern()+factorize()+solve()。

官方也提供了一个稀疏矩阵API的快速查找指南，点击查看。

4.参考资料

[1]http://eigen.tuxfamily.org/dox/group__TutorialSparse.html
[2]http://eigen.tuxfamily.org/dox/group__TopicSparseSystems.html
[3]http://eigen.tuxfamily.org/dox/group__SparseQuickRefPage.html

Menu