Eigen学习与使用笔记4

1.模块简介
2.旋转
- (1)2D旋转
- (2)3D旋转
  - 角轴表示
  - 四元数表示
3.平移
4.缩放
5.变换
6.参考资料

本篇博客主要记录Eigen的几何模块，处理2D、3D旋转、射影以及仿射等变换。使用几何模块需要导入头文件<Eigen\Geometry>。

1.模块简介

几何模块提供两种不同的几何变换：

抽象变换(Abstract transformation):旋转(Rotation)(角轴或四元素表示)、平移(Translation)、缩放(Scaling)。这些变换在Eigen中不是以矩阵形式表示，但它们可以与矩阵混合运算。
射影或仿射变换(Projective or Affine transformation):它们在Eigen中是用真正的矩阵表示。

以下是Eigen中不同变换所对应的数据类型：下面分别进行详细介绍。

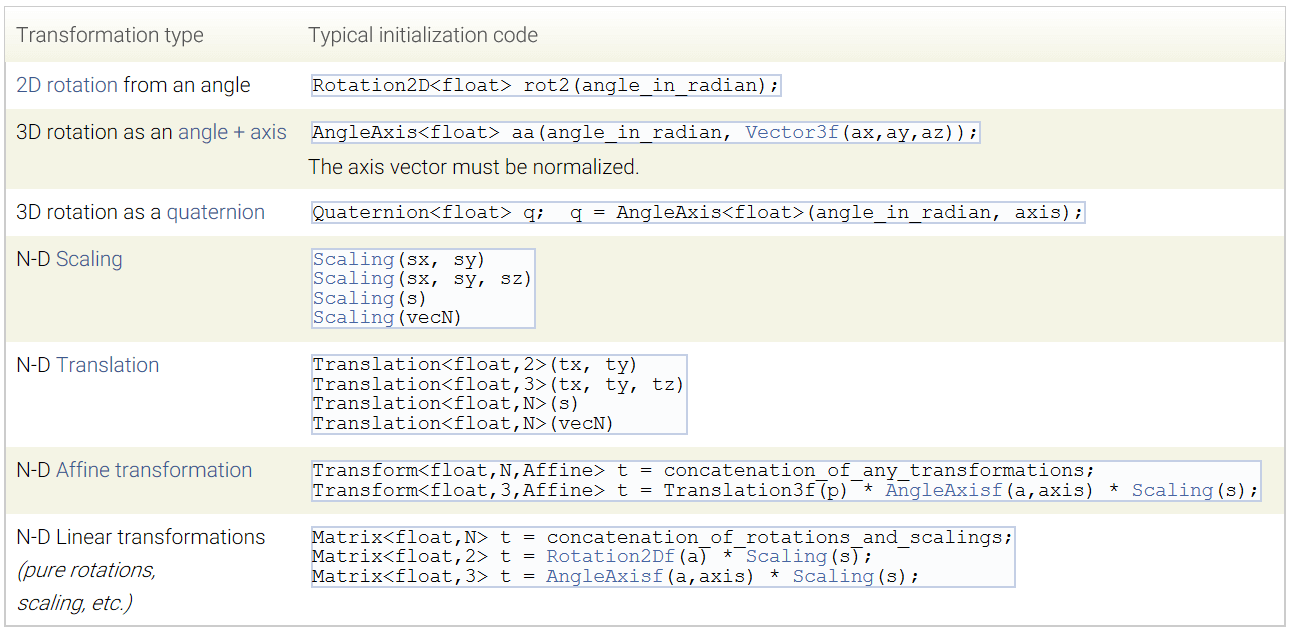
2.旋转

如上图所示，在Eigen中有多种方式可以表达旋转，如旋转角(2D)、角轴(3D)、四元数(3D)、旋转矩阵(2D&3D)等，它们各有特色。总的来说，对于多个向量进行批量旋转推荐使用旋转矩阵(Matrix)，这样操作起来更快捷。而其它情况下使用四元数(Quaternion)比较合适，因为它存储量小、快速、稳定。而像旋转角(Rotation2D)以及角轴(AngleAxis)，在实际使用中更多是为了方便创建旋转对象(Rotation Objects)而产生的的中间类型。在构建时需要注意凡是角度都用弧度表示。

(1)2D旋转

对于2D旋转，Eigen中用Rotation2D类对应，其创建方式和Matrix类似，需要一个模板参数表示数据类型，构造函数需要传入一个弧度表示的旋转角度。旋转顺序是顺时针为正，逆时针为负。除了这种方法还有2种重载的构造函数，分别传入的是2×2的旋转矩阵和已有的Rotation2D对象。此外也定义了Rotation2Dd和Rotation2Df对应于double和float数据类型，方便使用。另一个需要注意的一点是不要想当然地认为有Rotation2D就有Rotation3D类，这在Eigen中是没有的。

Rotation2D还提供了一些常用的成员函数方便使用，简单罗列如下：

.angle():返回弧度制表示的旋转角度
.cast():将当前对象转换为另一种类型的Rotation2D，如Rotation2Dd转到Rotation2Df。
.fromRotationMatrix():从一个2 × 2的旋转矩阵构建Rotation2D对象。换句话说，本函数可以提取旋转矩阵所表示的旋转角，像这样:.fromRotationMatrix(m).angle()即可返回弧度制表示的旋转角度。
.toRotationMatrix():将当前Rotation2D对象转换为2 × 2的旋转矩阵。
.isApprox():判断当前Rotation2D是否与给定Rotation2D近似相等，是的话返回true。判断精度由传入的第二个参数决定。
.inverse():返回以Rotation2D表示的当前旋转的逆旋转
.slerp():返回对起始Rotation2D和目标Rotation2D经过球面插值(spherical interpolation)得到的结果，在这里等于是线性插值，对于四元数不是。其结果范围与参数t有关。t=0时等于起始Rotation2D，t=1时等于目标Rotation2D，而t=n>1时，则等于n倍的目标Rotation2D。其使用注意事项在下面的代码中介绍。

下面是一些简单的使用示例。

#include <iostream>
#include <opencv2/opencv.hpp>
#include <Eigen/Dense>
#include <Eigen/Geometry>


using namespace std;
using namespace Eigen;
using namespace cv;

void drawRectangle(Mat &img, Point2i p1, Point2i p2, Point2i p3, Point2i p4, Scalar color, int thickness) {
    line(img, p1, p2, color, thickness, LINE_AA);
    line(img, p2, p3, color, thickness, LINE_AA);
    line(img, p3, p4, color, thickness, LINE_AA);
    line(img, p4, p1, color, thickness, LINE_AA);
}

Point2i cvtVector2Point(Vector2f vec) {
    Point2i p(int(vec(0, 0)), int(vec(1, 0)));
    return p;
}

int main() {

    Point2i lp1(100, 100), lp2(300, 100), lp3(300, 300), lp4(100, 300);
    Mat background = Mat(400, 800, CV_8UC3, Scalar(0, 0, 0));

    Rotation2Df pose1(0);
    Rotation2Df pose2(3.141592653);
    Vector2f rp1(-100, -100), loc1;
    Vector2f rp2(100, -100), loc2;
    Vector2f rp3(100, 100), loc3;
    Vector2f rp4(-100, 100), loc4;
    Vector2f center(600, 200);
    Matrix2f rot;

    int steps = 100;
    while (true) {
        for (int i = 0; i < steps; ++i) {
            float ratio = i * 1.0 / steps;
            // 注意这里插值的规则。取的是逆时针或顺时针旋转角最小的那个方向。
            // 例如如果让他内插0到270度，他会选择逆时针旋转90度而不是顺时针旋转270度。
            // 因此如果这里直接设置终止为2pi，他会直接选择逆时针旋转0度，结果就是没有旋转。
            // 所以插值的直接上下限不能超过180度，否则就可能和你预计的方向相反了。后面可以通过系数t则可以扩展上限，从而达到2pi。
            // 例如0-60 t设为6，0-90 t设为4，0-180 t设为2，这些都是等价的，且可以旋转360度
            rot = pose1.slerp(ratio * 2, pose2).toRotationMatrix();
            loc1 = rot * rp1 + center;
            loc2 = rot * rp2 + center;
            loc3 = rot * rp3 + center;
            loc4 = rot * rp4 + center;

            drawRectangle(background, lp1, lp2, lp3, lp4, Scalar(0, 0, 255), 2);
            drawRectangle(background,
                          cvtVector2Point(loc1),
                          cvtVector2Point(loc2),
                          cvtVector2Point(loc3),
                          cvtVector2Point(loc4),
                          Scalar(255, 255, 255), 2);
            circle(background, cvtVector2Point(loc1), 4, Scalar(255, 0, 0), -1, LINE_AA);
            circle(background, cvtVector2Point(loc2), 4, Scalar(0, 255, 0), -1, LINE_AA);
            circle(background, cvtVector2Point(loc3), 4, Scalar(0, 0, 255), -1, LINE_AA);
            circle(background, cvtVector2Point(loc4), 4, Scalar(0, 255, 255), -1, LINE_AA);

            imshow("img", background);
            waitKey(50);

            background = Scalar(0, 0, 0);
        }
    }
    return 0;
}

对应的CMake配置如下：

cmake_minimum_required(VERSION 3.12)
project(rotation2D)

set(CMAKE_CXX_STANDARD 11)

find_package(Eigen3 REQUIRED)
include_directories(${EIGEN3_INCLUDE_DIRS})

find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})

add_executable(rotation2D main.cpp)
target_link_libraries(${PROJECT_NAME} ${OpenCV_LIBS})

运行的效果如下动图所示。

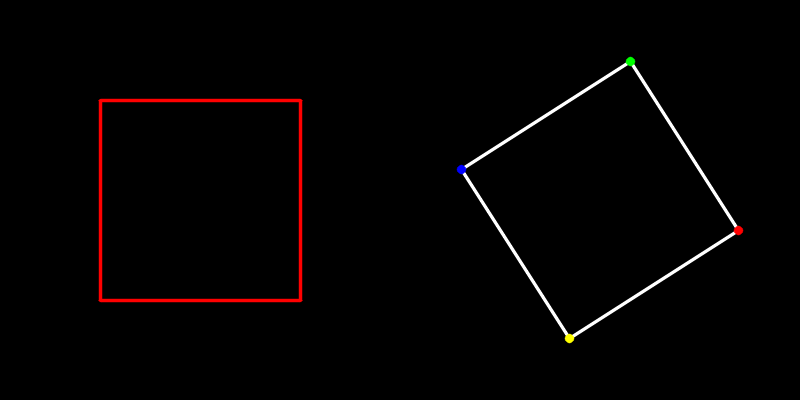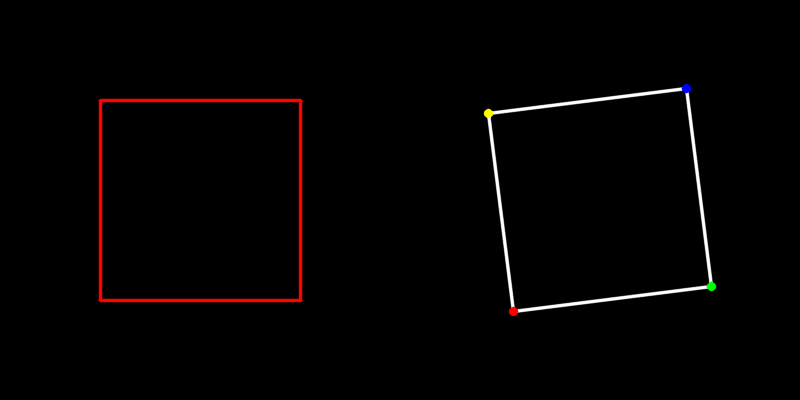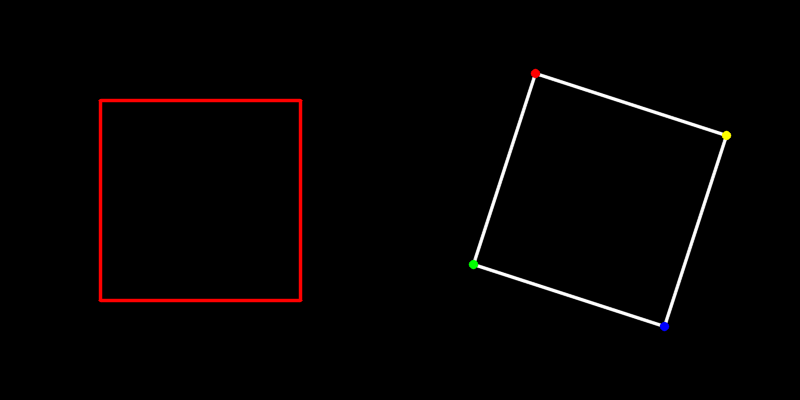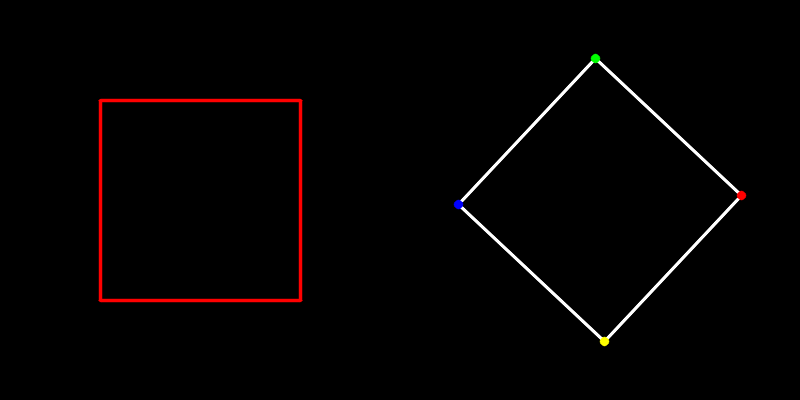
(2)3D旋转

3D旋转在Eigen中除了用常规的旋转矩阵(Matrix3d表示)外，有两种表示：AngleAxis和Quaternion。

角轴表示

AngleAxis是角轴表示法，顾名思义给定旋转角度和旋转轴即可。其创建方式符合Eigen的原则，传入数据类型作为模板参数。旋转角度以弧度表示，旋转轴为Vector类型的向量，注意向量必须要被归一化(vec.normalized()即可)。Eigen中也预先定义好了AngleAxisd和AngleAxisf两种方便使用。其也有一些成员函数，由于都是继承自RotationBase，很多都是类似的，这里简单罗列如下：

.angle():返回弧度制表示的旋转角度
.axis():返回该旋转的旋转轴向量
.cast():将当前AngleAxis对象转为另一种AngleAxis
.inverse():返回以AngleAxis表示的当前旋转的逆旋转
.isApprox():判断当前AngleAxis是否与给定AngleAxis近似相等，是的话返回true。判断精度由传入的第二个参数决定。
.fromRotationMatrix():从一个3 × 3的旋转矩阵构建AngleAxis对象。换句话说，本函数可以提取旋转矩阵所表示的旋转角，像这样:.fromRotationMatrix(m).angle()即可返回弧度制表示的旋转角度。
.toRotationMatrix():将当前AngleAxis对象转换为3 × 3的旋转矩阵。

简单使用示例如下：

#include <iostream>
#include <Eigen/Dense>
#include <Eigen/Geometry>


using namespace std;
using namespace Eigen;

int main() {
    // yaw-z pitch-y roll-x,并转成弧度
    float yaw = 10.3 * M_PI / 180;
    float pitch = 15.8 * M_PI / 180;
    float roll = 8.5 * M_PI / 180;
    Matrix3f m;
    m = AngleAxisf(roll, Vector3f::UnitX()) *
        AngleAxisf(pitch, Vector3f::UnitY()) *
        AngleAxisf(yaw, Vector3f::UnitZ());
    cout << m << endl;
    cout << "is unitary:" << m.isUnitary() << endl;
    AngleAxisf aa;
    aa.fromRotationMatrix(m);
    cout << aa.toRotationMatrix() << endl;
    return 0;
}

上述代码巧妙利用角轴方便地构建了一个旋转矩阵，实现了从欧拉角到旋转矩阵的转换。Matrix的成员函数isUnitary()表示该矩阵是否是一个酉矩阵(矩阵各列是否为标准正交基)。所谓酉矩阵定义是：n阶复方阵U的n个列向量是U空间的一个标准正交基，则U是酉矩阵(Unitary Matrix)。酉矩阵是正交矩阵往复数域上的推广。

四元数表示

Quaternion是四元数表示法，用于表示三维空间中的指向与旋转。关于什么是四元数这里不再多说，可以参考之前相关博客。相较于欧拉角和旋转矩阵，四元数的优势在于较小的存储量(4个数，相较于旋转矩阵的9个数)以及稳定的球面插值、没有奇异性(相较于欧拉角的万向锁)。它的缺点就是不够直观(相较于欧拉角)以及无法直接与向量、矩阵等运算(相较于旋转矩阵)。Quaternion的构造是标准Eigen格式：数据类型作为模板参数+构造参数，而且重载了多个构造函数，因此可以方便地从角轴、旋转矩阵等数据类型进行构造。特别需要注意四个数的传入顺序是w、x、y、z，对应w+xi+yj+zk。Eigen也提供了Quaternionf和Quaterniond方便使用。相关成员函数再罗列一下：

.w():返回四元数中的w分量(可修改)
.x():返回四元数中的x分量(可修改)
.y():返回四元数中的y分量(可修改)
.z():返回四元数中的z分量(可修改)
.coeffs():返回四元数的四个数(可修改)，可以对其进行索引[]获取值。需要注意的是返回顺序是x、y、z、w，和定义的时候是不一样的。
.toRotationMatrix()&.matrix():将当前Quaternion对象转换为3 × 3的旋转矩阵。另外说一下，Quaternion没有fromRotationMatrix()函数，但因为重载了构造函数，使其也可以由旋转矩阵构造。
.norm():返回四元数的模长
.squaredNorm():返回四元数平方的模长
.slerp():对两个四元数进行球面线性插值(Spherical linear interpolation，通常简称Slerp)，是四元数的一种线性插值运算，主要用于在两个表示旋转的四元数之间平滑差值。插值详细介绍可看参考资料[3]。
.inverse():返回以Quaternion表示的当前旋转的逆旋转
.normalize():归一化四元数，作用于其本身，没有返回值
.normalized():归一化四元数，返回归一化后的四元数
.Identity():返回一个表示单位旋转的四元数
.setIdentity():将自己设为表示单位旋转的四元数，set表示对自己修改。一般可用于对一个四元数变量进行初始化，如Quaternion::setIdentity()则将变量设置成了单位四元数
.conjugate():返回当前四元数的共轭四元数
.setFromTwoVectors():对自己进行修改，表示表示从向量a旋转到向量b的四元数。向量a、b不需要归一化，也不需要有相同模长。set表示对自己修改。
.FromTwoVectors():不对自己进行修改，返回一个表示从向量a旋转到向量b的四元数。向量a、b不需要归一化，也不需要有相同模长。
.angularDistance():返回两个四元数之间的角度距离
.cast():将当前Quaternion对象转为另一种Quaternion
.isApprox():判断当前Quaternion是否与给定Quaternion近似相等，是的话返回true。判断精度由传入的第二个参数决定。
.dot():四元数的点乘，结果是一个数。注意区别四元数的数乘和乘法，它们的结果还是四元数。
.vec():以向量形式返回四元数的虚部(可修改)，顺序为x、y、z。

简单使用示例如下：

#include <iostream>
#include <Eigen/Dense>
#include <Eigen/Geometry>


using namespace std;
using namespace Eigen;

int main() {
    AngleAxisf aaf1(0.1,Vector3f::UnitX());
    AngleAxisf aaf2(0.3,Vector3f::UnitY());
    Quaternionf qf1(aaf1),qf2(aaf2);
    cout<<qf1.coeffs()<<endl<<endl;
    cout<<qf2.coeffs()<<endl<<endl;

    Quaternionf inp_qf = qf1.slerp(0.4,qf2);
    cout<<inp_qf.coeffs()<<endl;
    return 0;
}

上述代码调用slerp()函数对两个四元数进行了插值。需要注意的是插值函数与之前说的一样，注意角度范围。

3.平移

相比于旋转，Translation会简单一些。这里2D和3D平移放在一起介绍。采用Eigen标准构造原则，构造示例如下：

Translation<float,2>(tx, ty)
Translation<float,3>(tx, ty, tz)
Translation<float,N>(s)
Translation<float,N>(vecN)

和之前一样，预先定义有Tanslation2f、Translation2d、Translation3f、Translation3d以供使用。多个平移合并用乘号而不是加号，需要注意。和旋转相比，它的成员函数也相对少一些，下面简单罗列：

.x():获取平移的x分量(可修改)
.y():获取平移的y分量(可修改)
.z():获取平移的z分量(可修改)，注意，千万不要对一个二维的Translation获取z分量，否则直接会运行报错的：Process finished with exit code 134 (interrupted by signal 6: SIGABRT)
.cast():将当前Translation对象转为另一种Translation
.vector()&.translation():返回当前平移的向量表示(可修改)，可以索引[]获取各分量
.Identity():返回单位平移(如二维是0,0，三维是0,0,0)
.inverse():返回以Translation表示的当前平移的逆平移
.isApprox():判断当前Translation是否与给定Translation近似相等，是的话返回true。判断精度由传入的第二个参数决定。

简单使用示例如下：

#include <iostream>
#include <Eigen/Dense>
#include <Eigen/Geometry>


using namespace std;
using namespace Eigen;

int main() {
    Translation2d t1(1,4);
    Translation2d t2(2,7);
    Translation2d t3;
    t3=t1*t2;
    cout<<t3.translation()<<endl;
    return 0;
}

上述代码将两个平移变换合并成了一个总的平移变换。

4.缩放

在Eigen中，缩放本质上是对角阵中对角线上不同位置的数。如1行1列为0.5，则表示对第一维缩放0.5倍，以此类推。所以Eigen中可以使用对角阵实现缩放，也可以使用一些预定义好的类型，如下：

/** \addtogroup Geometry_Module */
//@{
/** \deprecated */
typedef DiagonalMatrix<float, 2> AlignedScaling2f;
/** \deprecated */
typedef DiagonalMatrix<double,2> AlignedScaling2d;
/** \deprecated */
typedef DiagonalMatrix<float, 3> AlignedScaling3f;
/** \deprecated */
typedef DiagonalMatrix<double,3> AlignedScaling3d;
//@}

一些成员函数如下：

.diagonal():返回对角阵的对角线元素(可修改)
.inverse():返回一个逆缩放，逆缩放是指将当前缩放系数取倒数，如5的逆缩放就是0.2
.size():继承于Matrix的成员函数，返回矩阵元素个数
.cols():继承于Matrix的成员函数，返回矩阵列数
.rows():继承于Matrix的成员函数，返回矩阵行数

简单使用示例如下：

#include <iostream>
#include <Eigen/Dense>
#include <Eigen/Geometry>


using namespace std;
using namespace Eigen;

int main() {
    AlignedScaling2d s(1.5,0.4);
    Vector2d vec1(3,8);
    Vector2d vec2;
    vec2 = s*vec1;
    cout<<vec2<<endl;
    return 0;
}

上述代码对一个向量的不同维进行了不同尺度的缩放。

5.变换

在介绍变换之前，先简单回顾一下基本概念。以下变换都是在三维情况下。

一个欧式变换的矩阵表示形式如下：

\[\begin{pmatrix} R & t\\ 0^{T} & 1 \end{pmatrix}\]

旋转和平移各有三个自由度，因此一共有6个自由度，其保持长度、夹角、体积的不变性。也正因为如此，欧式变换又被称为刚体变换或刚体运动。

相似变换在欧式变换基础上有增加了缩放，矩阵表示形式如下：

\[\begin{pmatrix} sR & t\\ 0^{T} & 1 \end{pmatrix}\]

s为缩放尺度(三轴缩放相等，所以只算一个)，因此其一共有7个自由度，其保持体积比不变。相比于欧式变换的刚体，这里可以认为是非刚体运动。

仿射变换矩阵表示形式如下：

\[\begin{pmatrix} A & t\\ 0^{T} & 1 \end{pmatrix}\]

仿射变换与前两种变换最大的不同在于，其对于旋转部分只要求是可逆矩阵A，而并非需要旋转矩阵R(正交阵)。它保证的是线的平行性和体积(面积)比。这样导致的结果就是矩阵A有9个自由度，再加上平移的3个，一共有12个自由度。

射影变换的矩阵表示形式如下：

\[\begin{pmatrix} A & t\\ a^{T} & v \end{pmatrix}\]

左上角A为可逆矩阵，右上角t为平移，左下角a为缩放。若v不为0时，可对整个矩阵除以v，得到一个右下角为1的矩阵；否则得到一个右下角为0的矩阵。A有9个自由度、t有3个自由度、a有三个自由度，一共有15个自由度。自由度现实的理解就是对应可以求解的方程个数。

因此变换其实是从更一般的视角去看待上面提到的旋转、缩放、平移或者它们的混合，所以在实际场景用应用也最多。上面介绍的旋转、平移、缩放更多时候都是为新建或初始化这些变换准备的。在线代中，所有变换本质上都可以看作是矩阵相乘，Eigen中也不例外，各种变换都是Transform类的特例。Transform类可以看作是一个矩阵，所有的变换都可以调用成员函数.matrix()获得这个矩阵。例如对于一个仿射变换，其内部存储的矩阵如下：

\[\begin{pmatrix} linear & translation\\ 0...0 & 1 \end{pmatrix}\]

注意矩阵中不同部分的名称，Eigen中有获取这些部分的函数，名称是对应的。

对于变换的应用，在Eigen中使用乘号进行连接，且遵循左乘规则(变换在左边)。如v'=T x v，表示对v进行一个T变换得到v'。对于多个变换连接，同样遵循左乘原则，如t3 = t2 x t1。

实际使用中，常见的包括等距变换(Isometry)、仿射变换(Affine)、射影变换(Prospective)等Eigen已经预定义好了相关类，下面进行介绍。

(1)等距变换

等距变换(Isometry Transform)可以看作是维持任意两点距离不变的仿射变换，也称做欧氏变换、刚体运动，在实际场景中使用比较多。在Eigen中已经内置好了一些常用的等距变换可以直接调用，如下。

/** \ingroup Geometry_Module */
typedef Transform<float,2,Isometry> Isometry2f;
/** \ingroup Geometry_Module */
typedef Transform<float,3,Isometry> Isometry3f;
/** \ingroup Geometry_Module */
typedef Transform<double,2,Isometry> Isometry2d;
/** \ingroup Geometry_Module */
typedef Transform<double,3,Isometry> Isometry3d;

新建方法十分简单，直接类型名+变量名即可，赋值可以通过它的成员函数.rotate()和.translate()完成(须先初始化为单位阵)。三维等距变换是一个4×4的矩阵。但在构建一个变换前，你首先要想清楚两个问题：这个变换顺序(先平移后旋转or先旋转后平移)是什么？这个变换相对谁改变(固定轴or自身)？不同的答案会得到不同的结果，代码也不尽相同。以下是一个标准的新建并初始化按固定轴先平移再旋转变换的例子：

# include<iostream>
# include<Eigen\Dense>
# include<Eigen\Geometry>

using namespace std;
using namespace Eigen;

int main(){
	AngleAxisd rotation(3.1415926 / 4, Vector3d(1, 0, 1).normalized());
	Vector3d translation(1, 3, 4);
	Isometry3d T= Isometry3d::Identity();

	T.translate(translation);
	T.rotate(rotation);
	
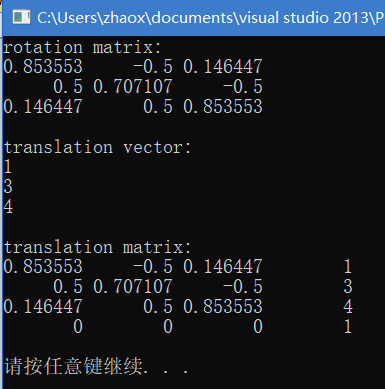
	cout << "rotation matrix:" << endl << rotation.toRotationMatrix() << endl << endl;
	cout << "translation vector:" << endl << translation << endl << endl;
	cout << "translation matrix:" << endl << T.matrix() << endl << endl;
	system("pause");
	return 0;
}

代码运行如下：上述代码中构建了一个角轴表示的旋转、一个平移向量以及一个初始的单位变换。注意这里必须要调用 Isometry3d::Identity()对它进行初始化(或者调用.setIdentity()设置)，后面的.translate()和.rotate()函数才有用。因为这些函数本质上都是矩阵乘法，而如果没初始化，Isometry3d中的元素全为0(或者非常大的负数)，这样等于是和0矩阵相乘，结果会不对。

如果你要说我就不初始化为单位阵行不行？也可以，那就不要调用.translate()和.rotate()函数，直接调用.matrix()函数获取对应的变换矩阵，然后手动自己设置(构造)，像下面这样。

# include<iostream>
# include<Eigen\Dense>
# include<Eigen\Geometry>

using namespace std;
using namespace Eigen;

int main(){
	AngleAxisd rotation(3.1415926 / 4, Vector3d(1, 0, 1).normalized());
	Vector3d translation(1, 3, 4);
	Isometry3d T;

	// 设置旋转R部分
	T.matrix().block(0, 0, 3, 3) = rotation.toRotationMatrix();
	// 设置平移t部分，.homogeneous()函数用于将平移向量变成对应的齐次表达形式
	T.matrix().col(3) = translation.homogeneous();
	// 设置最后一行
	T.matrix().row(3) = Vector4d(0, 0, 0, 1);

	cout << "rotation matrix:" << endl << rotation.toRotationMatrix() << endl << endl;
	cout << "translation vector:" << endl << translation << endl << endl;
	cout << "translation matrix:" << endl << T.matrix() << endl << endl;
	system("pause");
	return 0;
}

上面两种方式演示了基本的新建变换的步骤，可以发现很多成员函数如.translate()、.rotate()、.pretranslate()、.prerotate()等起了关键作用，这些函数是什么意思、怎么用，下面简单进行说明。

这些函数准确来说是用来“应用变换”的，变换在线代里即为矩阵相乘，这些函数将当前变换与输入的参数相乘，从而得到新的变换。有且仅当变换为单位阵时，这样等价于对变换赋值。A.translate(B)等价于A×B，而A.pretranslate(B)等价于B×A，对应于左乘和右乘的区别。

在应用角度而言，回到之前说的两个问题，这些函数就与它们有关。简单来说就是，凡是前面带pre的函数，其变化都是相对于上一步变化之前的状态进行的。这样说可能有些绕，举例说就是我要新建一个按固定轴平移旋转(世界坐标系下)、先平移后旋转的变换。但我首先设置了旋转，然后再设置平移。这个时候设置平移就不能用.translate()了，而应该用.pretranslate()。因为第一步已经对坐标系进行了旋转，后面的平移是在旋转后的坐标系中进行的，这显然和我设想的不一样。我需要在未旋转的坐标系上(世界坐标系)进行平移。下面代码演示了这种现象：

# include<iostream>
# include<Eigen\Dense>
# include<Eigen\Geometry>

using namespace std;
using namespace Eigen;

int main(){
	AngleAxisd rotation(3.1415926 / 4, Vector3d(1, 0, 1).normalized());
	Vector3d translation(1, 3, 4);
	Isometry3d T1 = Isometry3d::Identity();
	Isometry3d T2 = Isometry3d::Identity();
	Isometry3d T3 = Isometry3d::Identity();

	T1.translate(translation);
	T1.rotate(rotation);

	T2.rotate(rotation);
	T2.pretranslate(translation);

	T3.rotate(rotation);
	T3.translate(translation);

	cout << "rotation matrix:" << endl << rotation.toRotationMatrix() << endl << endl;
	cout << "translation vector:" << endl << translation << endl << endl;
	cout << "translation matrix1:" << endl << T1.matrix() << endl << endl;
	cout << "translation matrix1:" << endl << T2.matrix() << endl << endl;
	cout << "translation matrix1:" << endl << T3.matrix() << endl << endl;
	system("pause");
	return 0;
}

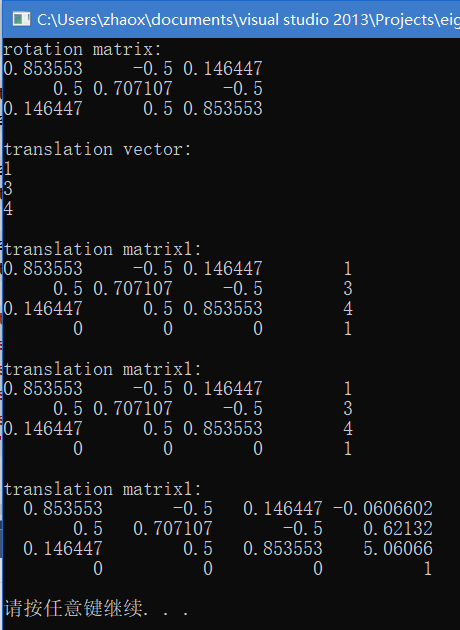
运行结果如下：在代码中建了3个变换，其中1和2是等价的，而3的平移部分作为对比没有使用.pretranslate()，可以看到和我们预期的不一样。其实这等于是按自身进行变换了，这在欧拉角的旋转中倒是有用。之前说过欧拉角有两种不同的定义方式：按自身旋转和按固定轴旋转。

常用的一些成员函数列举如下：

.translation():无参数，返回当前变换平移部分的向量表示(可修改)，可以索引[]获取各分量
.translationExt():无参数，如果当前变换是仿射的话，返回平移部分(可修改)；如果是射影变换的话，返回最后一列(可修改)
.translate():有参数，用于在当前变换上应用右乘，A.translate(B)等价于A×B
.pretranslate():有参数，用于在当前变换上应用左乘，A.pretranslate(B)等价于B×A
.rotation():无参数，返回只读的当前变换的旋转部分，以旋转矩阵表示
.rotate():有参数，用于设置当前变换的旋转部分，输入参数可以为角轴、四元数、旋转矩阵等。A.rotate(B)等价于A×B
.prerotate():有参数，用于设置当前变换的旋转部分，输入参数可以为角轴、四元数、旋转矩阵等。A.prerotate(B)等价于B×A
.matrix():返回变换对应的矩阵(可修改)
.cols():变换对应矩阵的列数
.rows():变换对应矩阵的行数
.linear()&.linearExt():返回变换的线性部分，对于Isometry而言就是旋转对应的旋转矩阵
.inverse():返回当前变换的逆变换
.Identity():返回一个单位变换，一般可用于Isometry的初始化中，将变换设为一个单位阵：Isometry3d::Identity()
.setIdentity():将当前变换变成单位变换，变换对应的矩阵变成单位阵，也可用于初始化赋值
.cast():将当前类型的变换转换为其它类型的变换，如Isometry3d转Isometry3f
.data():返回一个指向变换内部矩阵的指针，矩阵按照列优先存储
.computeRotationScaling():将当前变换的线性部分分解成rotation和scaling的乘积
.computeScalingRotation():将当前变换的线性部分分解成scaling和rotation的乘积
.fromPositionOrientationScale():从一个3D对象的位置、指向以及缩放来设置一个变换
.prescale():有参数，用于在当前变换上应用右乘，A.translate(B)等价于A×B
.scale():有参数，用于在当前变换上应用右乘，A.translate(B)等价于A×B
.preshear():只针对2D情况，沙尔变换，有参数，用于在当前变换上应用左乘，A.preshear(B)等价于B×A
.shear():只针对2D情况，沙尔变换，有参数，用于在当前变换上应用右乘，A.shear(B)等价于A×B
.affine():无参数，返回当前变换的仿射部分(可修改)，对于Isometry3d而言，返回的是一个4×3的矩阵
makeAffine():将变换对应的矩阵的最后一行设为0,0,…,1
.isApprox():判断当前Isometry是否与给定Isometry近似相等，是的话返回true。判断精度由传入的第二个参数决定。

简单使用示例如下：

# include<iostream>
# include<Eigen\Dense>
# include<Eigen\Geometry>

using namespace std;
using namespace Eigen;

int main(){
	Isometry3d transform;
	transform.setIdentity();

	transform.translate(Vector3d(1.5, 2, 3));
	transform.rotate(AngleAxisd(0.1, Vector3d::UnitX()));
	cout << "transform matrix:\n" << transform.matrix() << endl << endl;

	Vector3d vec1(4.3, 5, 3.2),vec2;
	vec2 = transform*vec1;
	cout << vec1 << endl << endl;
	cout << vec2 << endl;
	system("pause");
	return 0;
}

构造了一个三维刚体变换并将其应用到了vec1这个向量上。

(2)仿射变换

仿射变换是空间直角坐标变换的一种，保留线的平行性。仿射变换一般按照TRSI的顺序进行构建，T-translation，R-rotation，S-scaling，I-identity。

Transform<float,N,Affine> t = concatenation_of_any_transformations;
Transform<float,3,Affine> t = Translation3f(p) * AngleAxisf(a,axis) * Scaling(s);

为了方便Eigen中已经定义好了一些常用类型，如下：

/** \ingroup Geometry_Module */
typedef Transform<float,2,Affine> Affine2f;
/** \ingroup Geometry_Module */
typedef Transform<float,3,Affine> Affine3f;
/** \ingroup Geometry_Module */
typedef Transform<double,2,Affine> Affine2d;
/** \ingroup Geometry_Module */
typedef Transform<double,3,Affine> Affine3d;

由于仿射变换的成员函数和Isometry是一模一样的，这里就不再介绍了。下面是一个简单的使用示例。

# include<iostream>
# include<Eigen\Dense>
# include<Eigen\Geometry>

using namespace std;
using namespace Eigen;

int main(){
	Affine2d affine;
	affine.setIdentity();
	affine.translate(Vector2d(1.2, 3));
	affine.rotate(Rotation2Dd(0.1));
	cout << "affine matrix:\n" << affine.matrix() << endl << endl;
	Matrix<double, 2, 3> vecs1,vecs2;
	vecs1 << 1, 2, 3, 4, 5, 6;
	cout << "original vectors:\n" << vecs1 << endl << endl;
	vecs2 = affine*vecs1;
	cout << "affined vectors:\n" << vecs2 << endl;
	system("pause");
	return 0;
}

利用2D仿射变换对多个向量进行了批量变换。

(3)射影变换

射影变换是最一般的变换，其保证的是接触平面的相交或相切。Eigen中预定好的一些类型如下。

/** \ingroup Geometry_Module */
typedef Transform<float,2,Projective> Projective2f;
/** \ingroup Geometry_Module */
typedef Transform<float,3,Projective> Projective3f;
/** \ingroup Geometry_Module */
typedef Transform<double,2,Projective> Projective2d;
/** \ingroup Geometry_Module */
typedef Transform<double,3,Projective> Projective3d;

它的成员函数和Isometry也是一模一样的，这里也不再介绍了。下面是一个简单的使用示例。

# include<iostream>
# include<Eigen\Dense>
# include<Eigen\Geometry>

using namespace std;
using namespace Eigen;

int main(){
	Projective3d prj;
	prj.setIdentity();
	cout << prj.matrix() << endl;
	system("pause");
	return 0;
}

6.参考资料

[1]http://eigen.tuxfamily.org/dox/group__TutorialGeometry.html
[2]http://eigen.tuxfamily.org/dox/classEigen_1_1Rotation2D.html
[3]https://www.cnblogs.com/21207-iHome/p/6952004.html
[4]http://eigen.tuxfamily.org/dox/classEigen_1_1AngleAxis.html
[5]http://eigen.tuxfamily.org/dox/classEigen_1_1Quaternion.html
[6]http://eigen.tuxfamily.org/dox/classEigen_1_1Translation.html
[7]http://eigen.tuxfamily.org/dox/classEigen_1_1Transform.html#adf4c6d97bd3f10edfa95bb04331ec8ed
[8]http://eigen.tuxfamily.org/dox/classEigen_1_1Transform.html
[9]https://stackoverflow.com/questions/51315825/precedence-in-eigen-transformations-and-difference-between-pretranslate-and-tran
[10]https://stackoverflow.com/questions/25504397/eigen-combine-rotation-and-translation-into-one-matrix

Menu

Eigen学习与使用笔记4

Sep 3,2019 18202 words 66 min

1.模块简介

2.旋转

(1)2D旋转

(2)3D旋转

角轴表示

四元数表示

3.平移

4.缩放

5.变换

(1)等距变换

(2)仿射变换

(3)射影变换

6.参考资料