- 1.Cemera Modeling
- 2.Single View Geometry
- 3.Glimpse on Vanishing Points
- 4.Perspective Projection
- 5.Point-Line Duality
- 6.Rotations and Translations
- 7.Pinhole Camera Model
- 8.Focal Length and Dolly Zoom Effect
- 9.Intrinsic Camera Parameter
- 10.3D World to First Person Transformation
- 11.How to Compute Intrinsics from Vanishing Points
- 12.Camera Calibration
本篇博客是Coursera上宾大的《Robotics:Perception》的笔记，课程网址是这里。全篇笔记截图较多(84张)，建议在网速较好的情况下浏览或缓冲等待一会后再阅读。 如果实在无法正常浏览，点击这里下载本文所有图片，提取码：p68r。
1.Cemera Modeling
Camera = chip + lens
透镜成像模型示意图。推荐佳能的一段介绍动画，十分生动形象地展示了成像过程，点击查看。
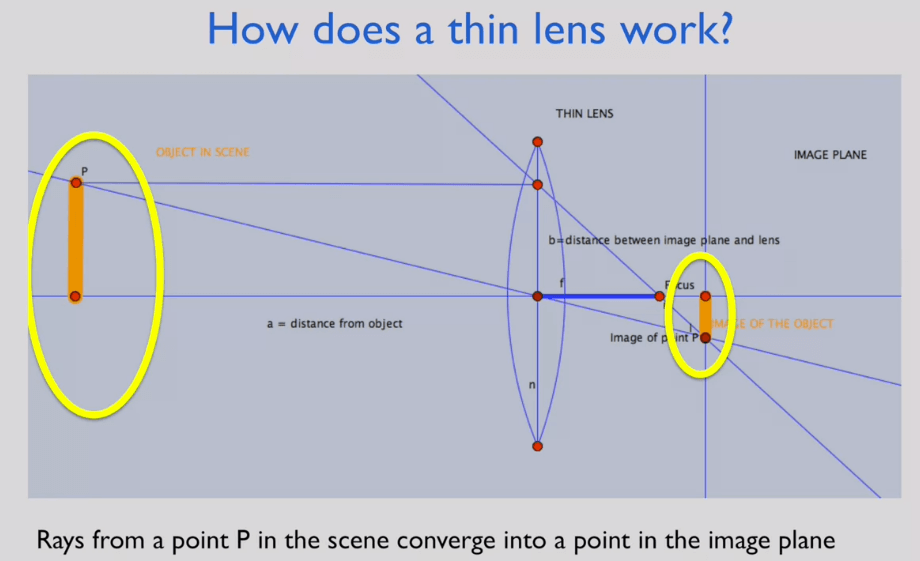物体到透镜的距离记为a(物距)，像平面到透镜的距离记为b(像距)，焦点到透镜的距离记为f(焦距)。这里需要注意的是在透镜成像模型中焦距与像距不等f≠b。
透镜成像模型有如下性质：
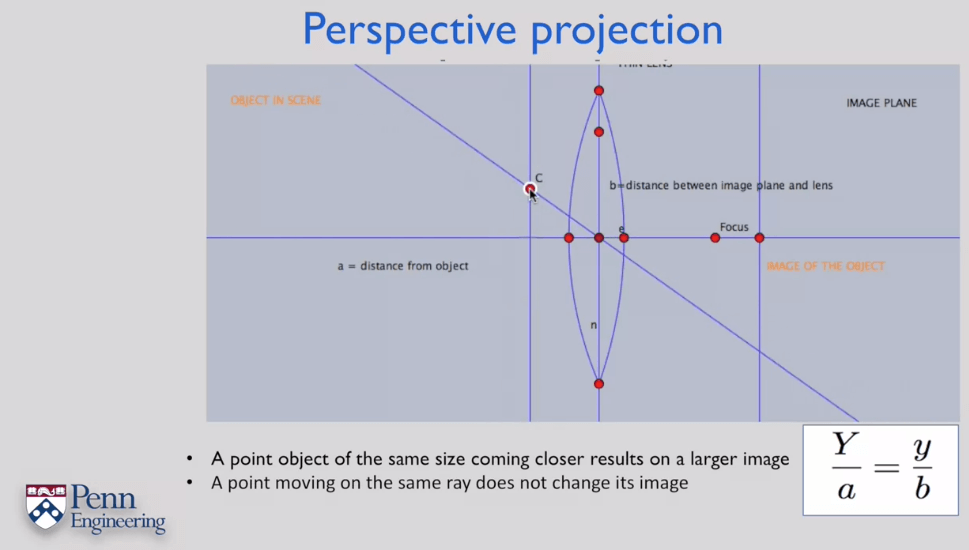
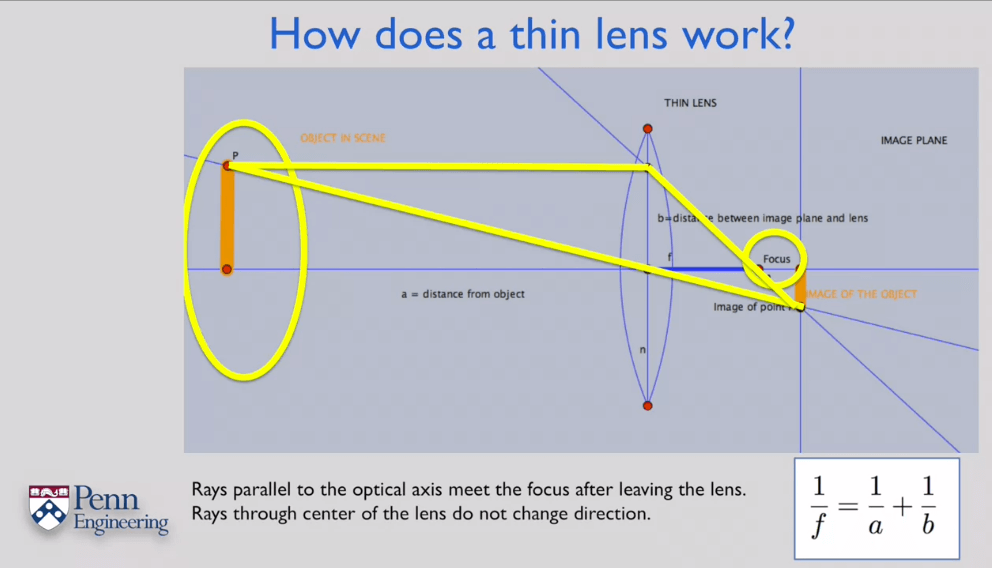所有平行于主光轴的光经过透镜折射都会交于一点，这点被称为焦点；所有经过透镜中心的光线不改变入射方向。基于以上内容，利用三角形相似原理，可以推导出成像方程，推导用示意图如下：
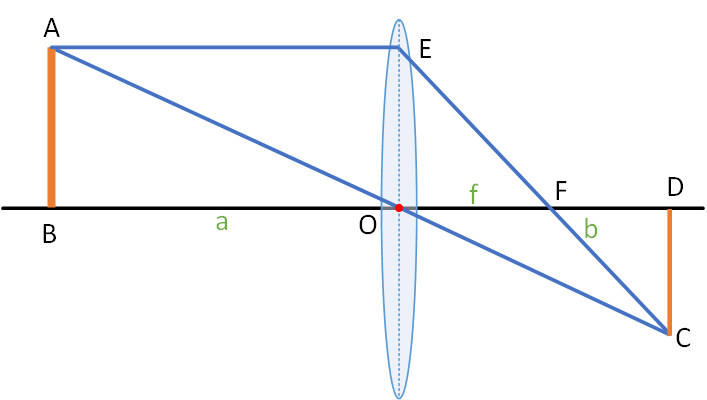△ABO与△CDO相似，所以有：
而由△EOF与△CDF相似，有：
\[\frac{OE}{CD}=\frac{OF}{FD}\]由于ABOF为平行四边形，AB=OE，所以联立上面两式有：
\[\frac{AB}{CD}=\frac{BO}{OD}=\frac{OF}{FD}\]取等式右边两项，并以对应的长度代替，有：
\[\frac{a}{b}=\frac{f}{b-f}\]对上式化简：
\[a(b-f)=bf\] \[ab-af=bf\]等式两边同乘\(1/abf\)，有：
\[\frac{1}{f}-\frac{1}{b}=\frac{1}{a}\]最后移项整理可得透镜成像方程：
\[\frac{1}{f}=\frac{1}{a}+\frac{1}{b}\]当某个点发出的平行于主光轴、不平行于主光轴两种光线在像平面上汇集于一点时，可以获得最清晰的图像。可以通过调整像面至透镜的距离b来调整它们在像平面上的交点。这个过程即称为对焦。在现代相机中，对焦过程一般通过手动转动对焦环或者镜头内置的对焦马达改变像面的位置，从而获得最清晰的图像。如果焦没对上就会出现模糊的情况(由点变成一小段线段)，且此时成像方程也不再满足，如下红色线段所示。
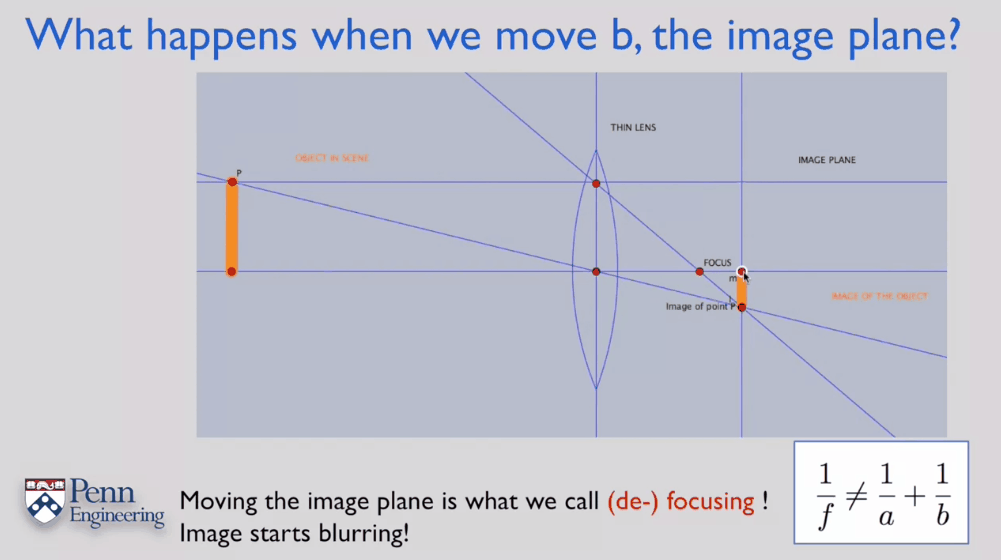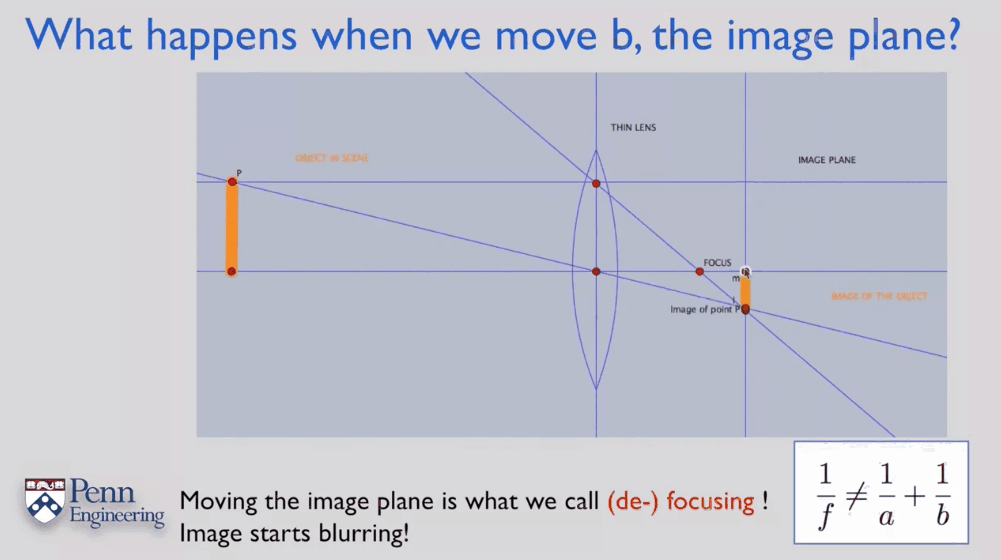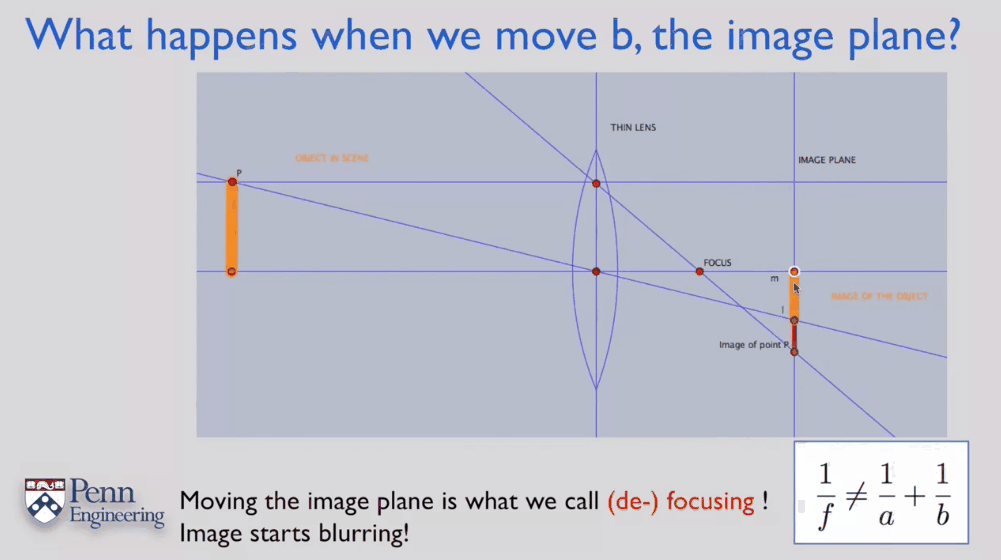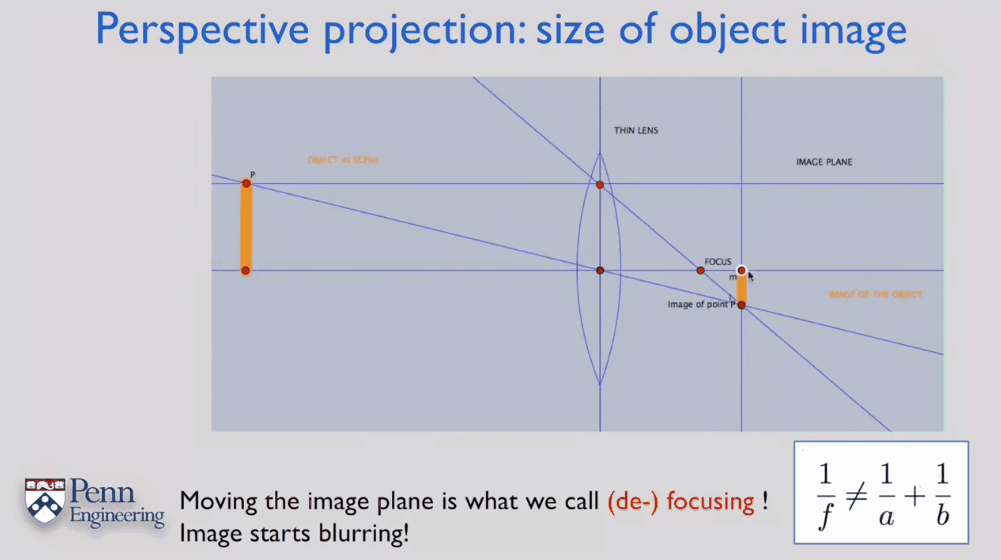
这里需要注意：由焦距的定义，对焦这个过程是不会改变焦距的！焦距是一个镜头(透镜)的固有属性之一。对焦移动的是像平面，改变的是像距b。会改变焦距的过程是调焦或者说变焦，这在很多变焦镜头中有所应用。在外界条件不变的情况下，减小焦距会让物体变大。
如果我们只考虑从透镜中心经过的光线(没有透镜折射)，这其实就是前面介绍的小孔成像模型了。根据三角形相似原理，成像大小与物距a、像距b的关系示意如下。简单一句话是近大远小。
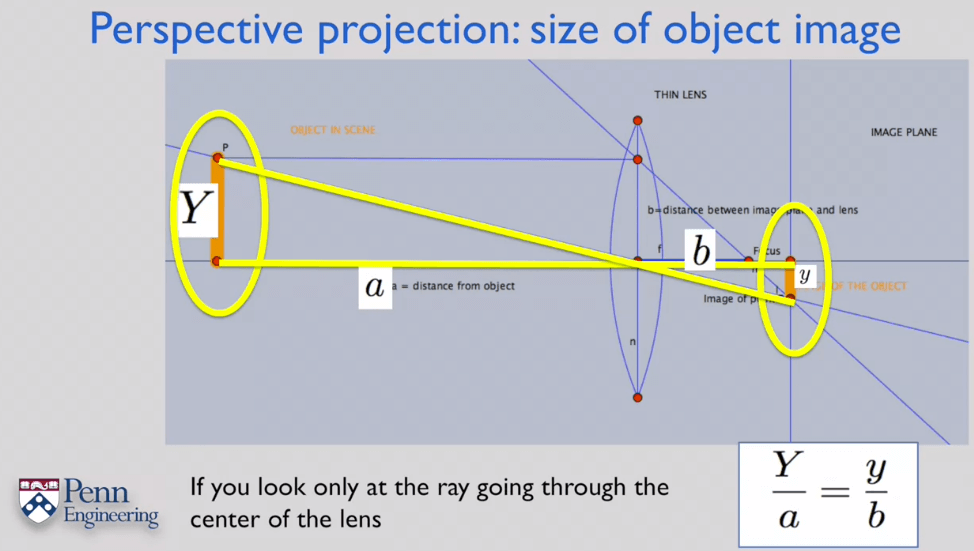
2.Single View Geometry
灭点Vanishing Point
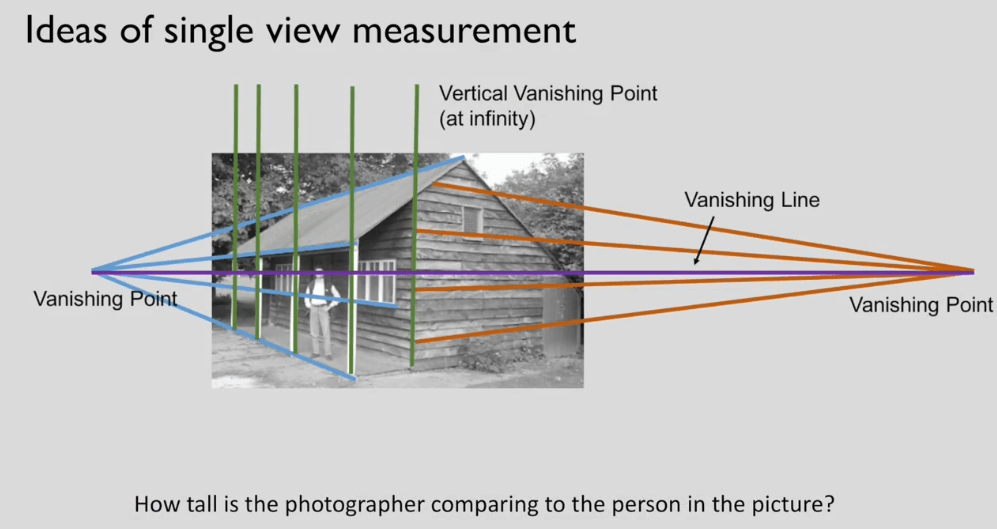在一个图片中可以有很多个灭点，这些灭点连接起来就组成了地平线(horizon)，又叫做灭影线(Vanishing Line)。
3.Glimpse on Vanishing Points
灭点测量物体高度实验
灭点的作用之一是可以基于一些已知高度的物体，利用灭点，进而测量未知物体的高度。如下是拍摄的一盒酸奶和眼药水的照片，经过测量，酸奶盒的高度是10.3cm。现在想要根据这张照片测量眼药水的高度。
具体做法是先根据酸奶盒两组平行的边做出两个灭点，然后连接两个灭点即可得到灭影线。然后连接酸奶盒的底点与眼药水的底点，交灭影线于一点，再连接该点与眼药水顶点交酸奶盒竖直边缘与一点，将该角点与酸奶盒底点连接，得到的线段长度即为眼药水的高度。作图如下图所示(看不清可以右键查看原图)。
局部放大图如下所示。
眼药水与酸奶盒高度对比图如下。
可以看到眼药水大约到“杆菌”两个字，而通过灭点测量的高度也在“杆菌”附近，基本是准确的。最后根据长度对应关系可以测得眼药水高度约为5.3cm。以上实验的原始数据及原图点此查看，提取码：n5ks。
4.Perspective Projection
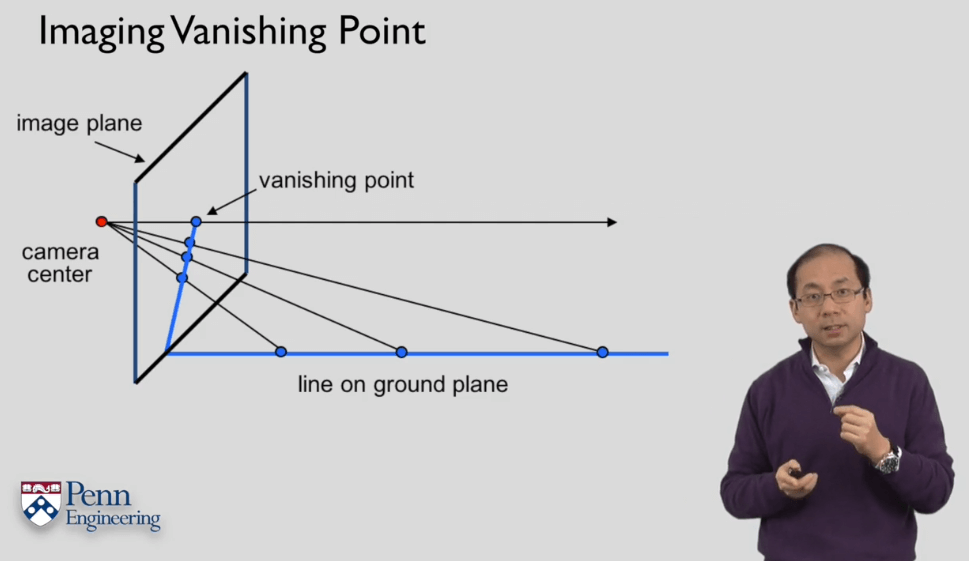
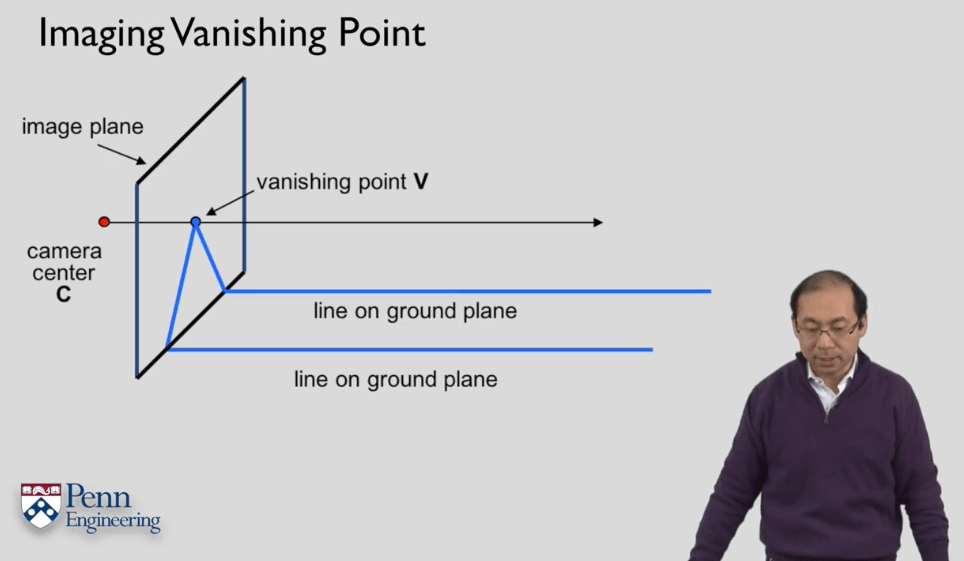
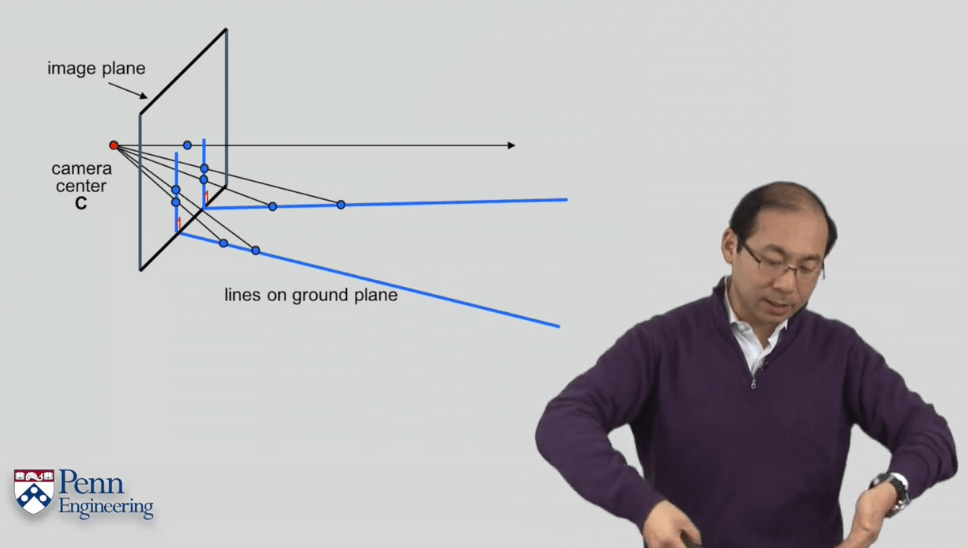
在投影平面中的点可以看作是以相机光心为起点，指向该点，延伸到无穷远处的一条射线。在这条射线上的所有点在像平面上都有相同的坐标。
在齐次坐标下，点看作是一条三维射线，线看作是一个三维平面。
点的齐次坐标表示
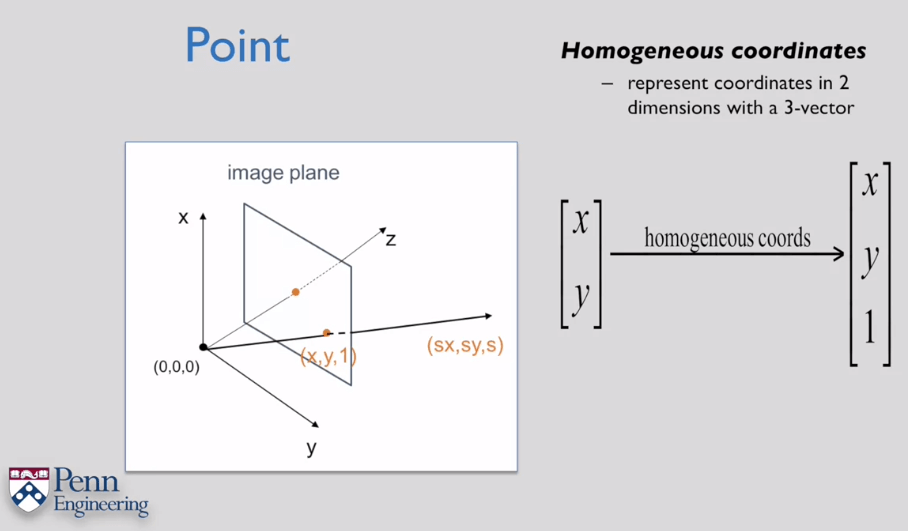
像平面上的点可以用如下方式表示，认为像面到原点的距离为1。在这样的场景下，像面上的一个点不再是一个点，而是一个相机光心为起点(0,0,0)，经过该点(x,y,1)，并延伸至无穷远处的一个向量。这个概念很重要，后续在推导线的齐次坐标时会用到。
线的齐次坐标表示
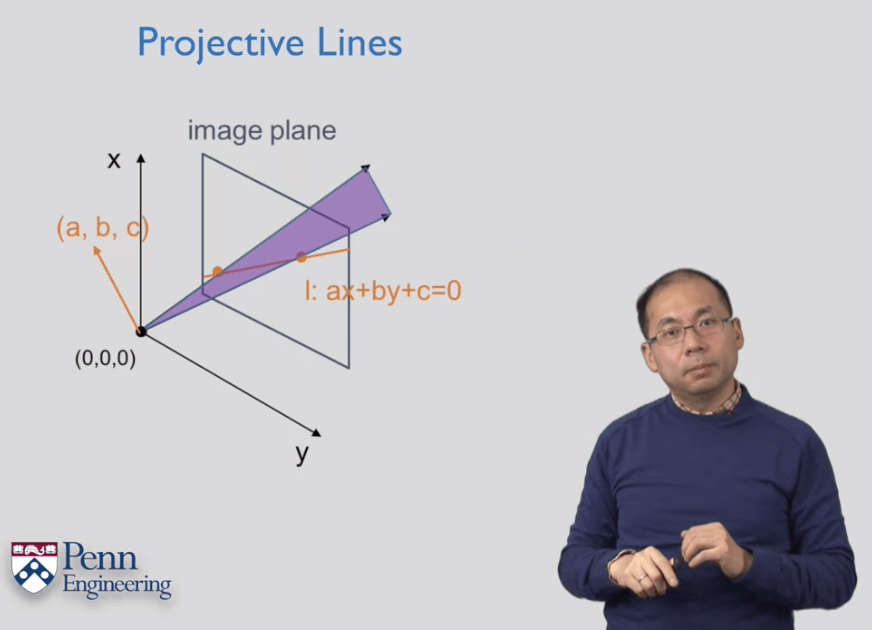这里的a、b、c的意义是构成了一个过坐标原点，由线段两个端点出发的射线所构成平面的法向量。
直线的其它表达形式及相互关系如下：
简而言之，在齐次坐标下，直线通过两个向量做叉乘进行定义。两个点可以唯一确定一条线，而点在其次坐标下又是由向量表示的。所以齐次坐标下线可以理解为这两条射线所构成的平面与像面的交线。这个面与线是一一对应的，而为了表示这个面，可以用过原点的法向量唯一描述。在数学上等价于对两个向量做叉积。
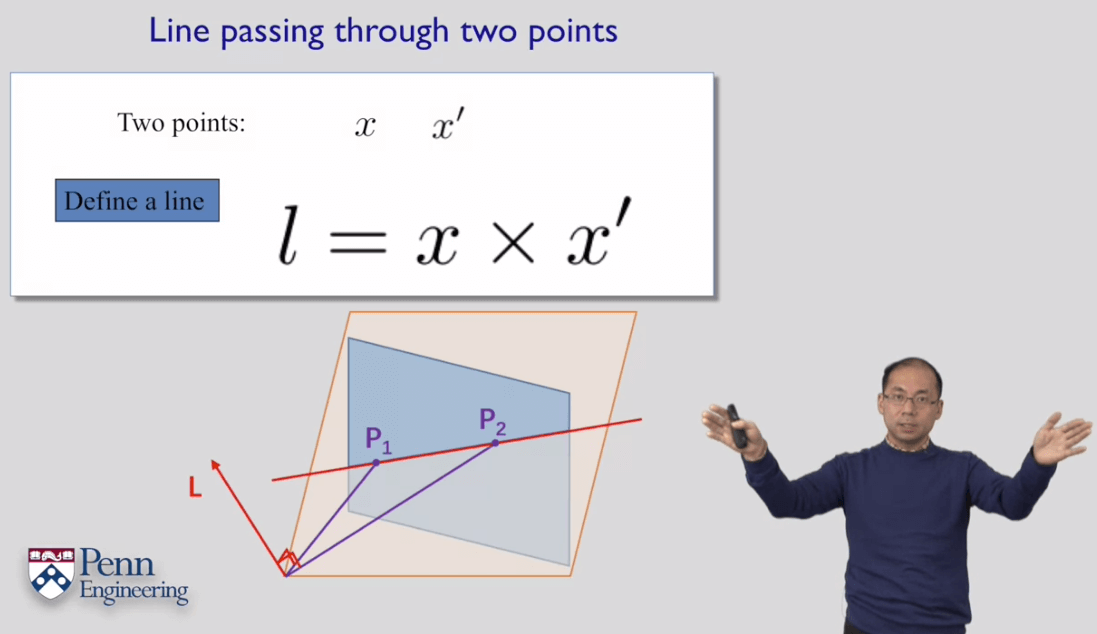向量叉乘的计算法则如下：
在Matlab中用cross(a,b)计算。需要注意的是要在像面上可视化这个向量(注意不是这条线本身，而是表达这条线的向量，这条线本身利用叉乘得到的结果直接画图就可以)，要对得到的向量除以\(\sqrt{a^{2}+b^{2}}\)，这样可以使前两个分量和前面说的sinθ和cosθ对应。向量各分量的绝对大小不重要，重要的是各分量间的关系。
一个简单计算直线的例子如下。
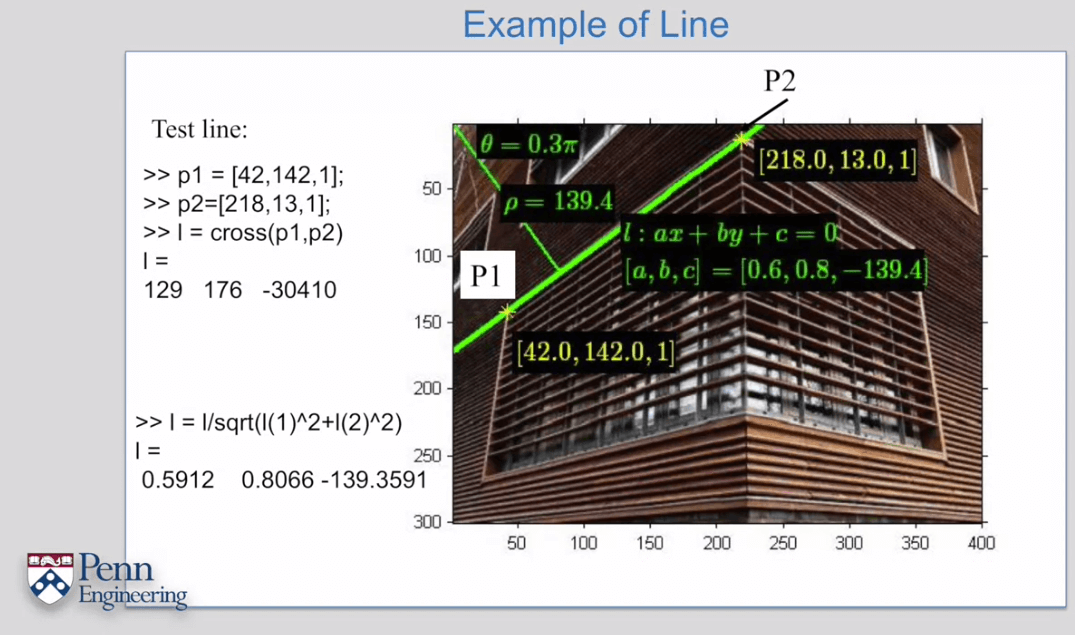在表达直线的向量中有一些比较特殊的形式如下：
-
对于直线
(a,b,0)表示该向量在z方向没有分量，它表示所有经过像平面中心的线。而且可以想象的是，如果这条线在中心点上方，z分量应该是负的；在下方，z应该是正的；右边z为正，左边z为负。可以自己拿手比划一下就知道了。 -
对于直线
(0,0,1)表示图像平面的地平线，不是我们在图片中看到的地平线。
两条线的交点计算
在投影中线不再当成线，而是一个过原点的平面。可以这样想：P在直线L1上，所以原点到P的向量OP一定垂直于OL1，同理OP也一定垂直于OL2。也就是说OP垂直于OL1和OL2所构成的平面，那么也就是说OP是OL1-OL2平面的法向量。因此要求OP，只需要对OL1、OL2做叉乘即可，而不需要像传统方法一样解方程了。
在明白了这个思想后，就可以利用齐次坐标下的线方便地算出灭点了，而不再需要靠人工测量。思路也很简单，灭点即是图像中两条现实世界中平行线的交点，所以在获得了表达两条线的向量之后，直接叉乘即可得到结果(交点)。注意如果为了在像平面中正确可视化交点，记得正则化向量的第三个分量(z分量)为1。
简单计算示例如下：
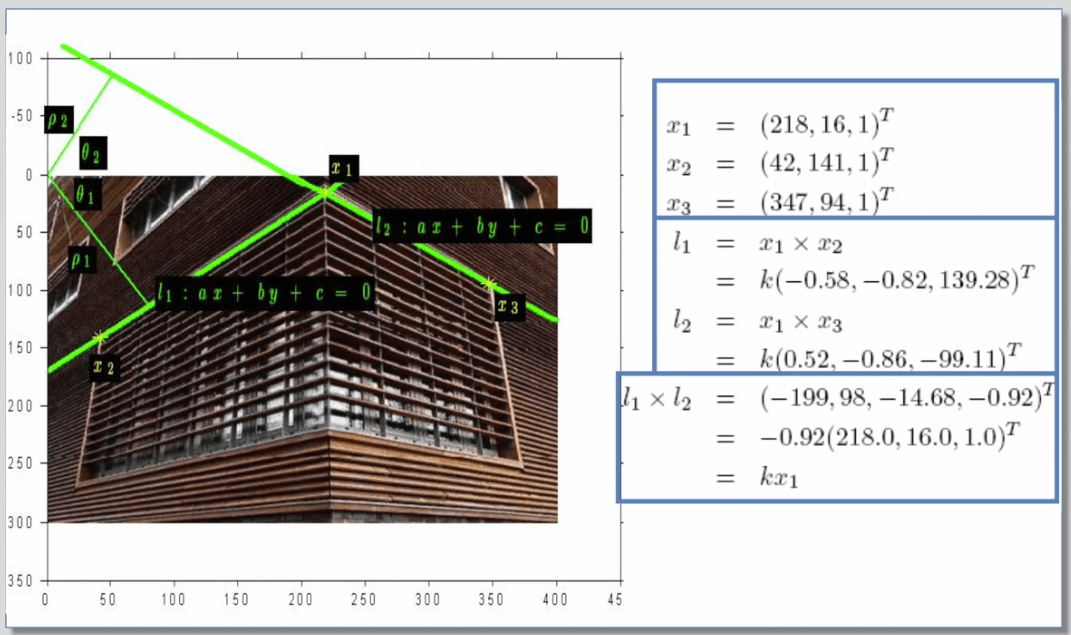
5.Point-Line Duality
对于一个向量，既可以理解为表示一个点，也可以理解为表示一条线，所以存在二元性。例如向量(1,2,3)，若将其按z分量归一化有(1/3,2/3,1)，表示一个像面上的点。也可以理解为这是一条直线，这个直线与原点构成平面的法向量是它。
无穷远处的点
两直线交点为(x,y,0)情况
所有形如(x1,x2,0)的交点都表示该两条线在无穷远处的交点，进而说明这两条线平行。
无穷远处的直线
一条无穷远处的线形式都是(0,0,1)。
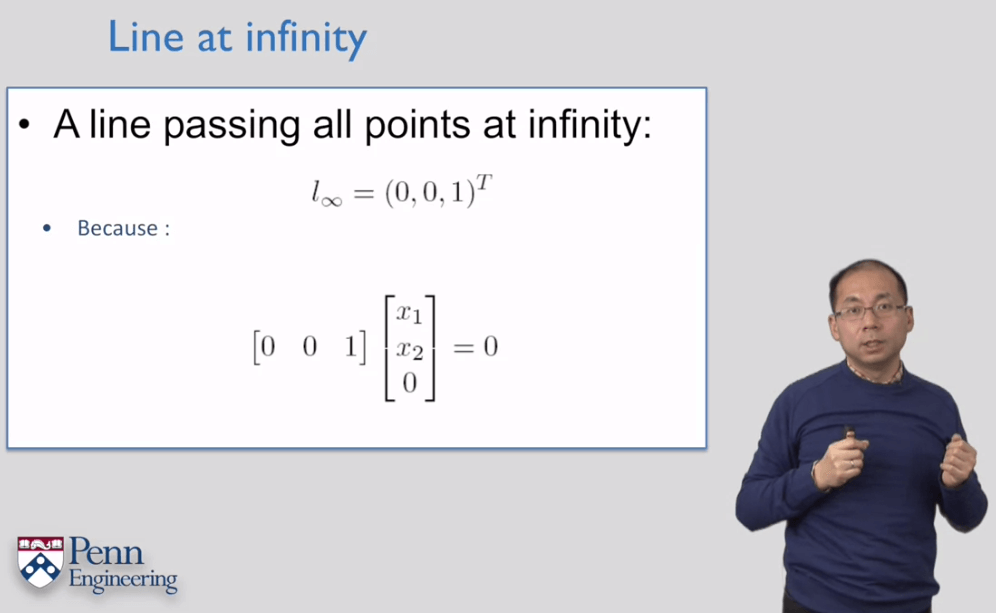
6.Rotations and Translations
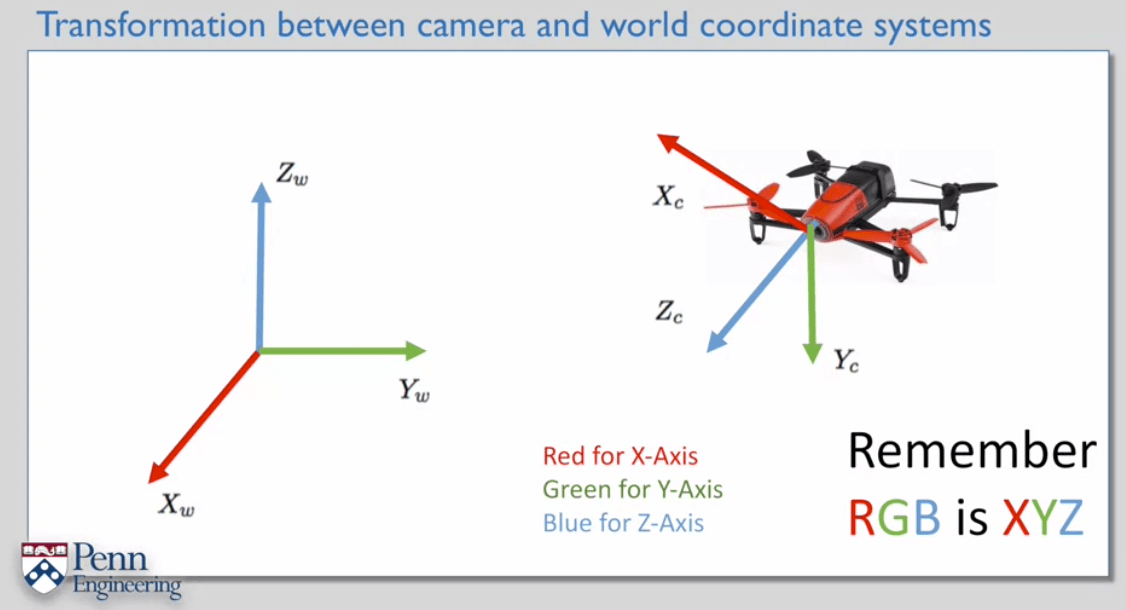
习惯上x轴用红色表示，y轴绿色表示，z轴蓝色表示。\({}^{c}\textrm{P}\)表示P点在Camera坐标系下的坐标，\({}^{w}\textrm{P}\)表示P点在World坐标系下的坐标。
\({}^{c}\textrm{R}_{w}\)
表示从Camera坐标系到World坐标系的旋转，
\({}^{c}\textrm{T}_{w}\)
表示从Camera坐标系到World坐标系的平移。
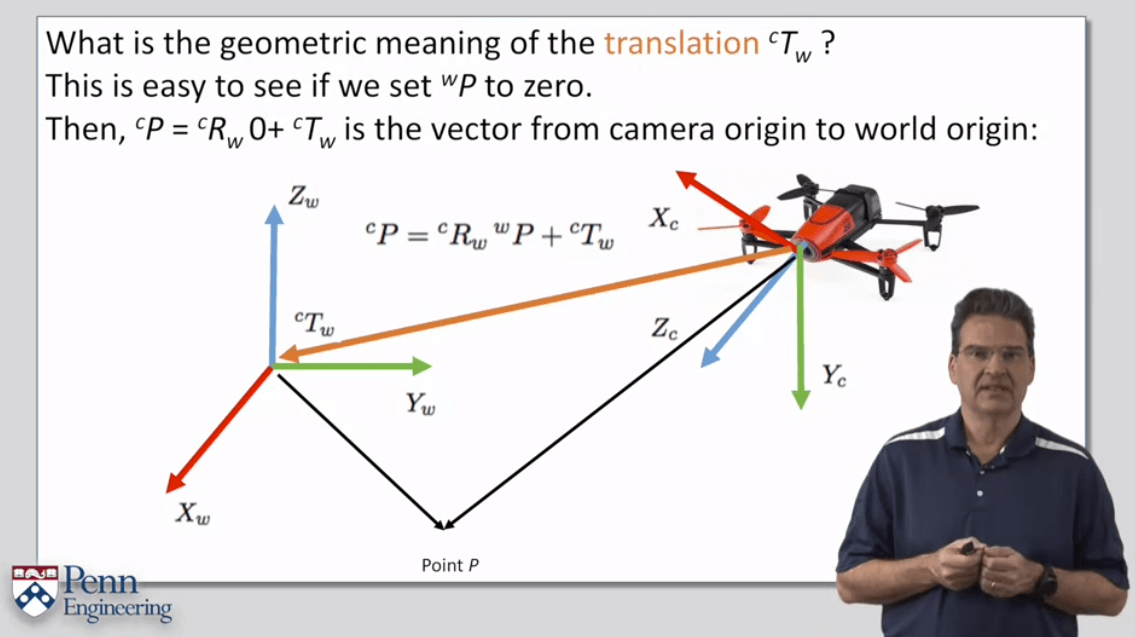理解平移的几何意义不妨先假设s上式中某点P在世界坐标系下的坐标为0，那么这样我们就可以得到一个在相机坐标系下表示的、从相机坐标系原点出发、指向世界坐标系原点的向量，这个向量就代表了平移。需要注意的是当我们写这个公式的时候，这里的平移T指的是从相机到世界坐标系的平移，而不是反过来从世界到相机的平移。
对于旋转矩阵可以看作是三个列向量r1、r2、r3。每个列向量都是世界坐标系坐标轴在相机坐标系下的表示，如r1表示世界坐标系的x轴在相机坐标系下的表示(The first column is the x axis of the world with respect to the camera)。根据上面的介绍，下图的变换就可以理解了。下面的变换发生在Y-Z平面上。
世界坐标系的x轴在相机坐标系下的表示为(-1,0,0)，y轴为(0,0,-1)，z轴为(0,-1,0)，所以旋转矩阵如上图所示。而平移则是世界坐标系的原点相对于相机坐标系的平移，沿y轴正向移动5，z轴正向移动10，所以为(0,5,10)。在得到旋转矩阵后，还需要做验证，看其是否满足正交阵的性质：转置等于逆。
另一个稍微复杂的例子。
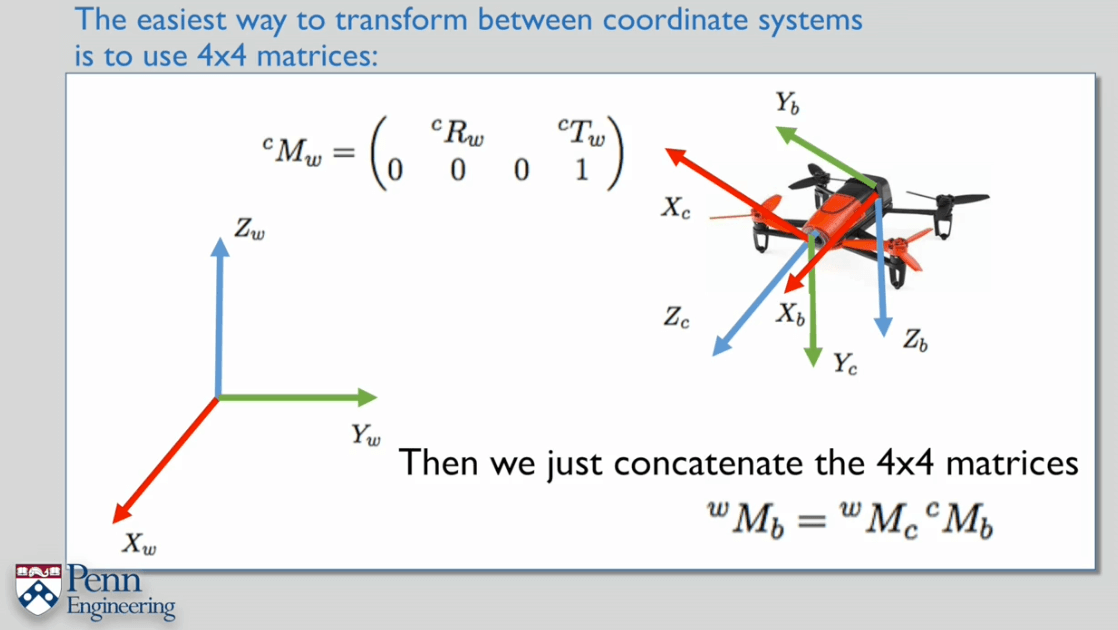
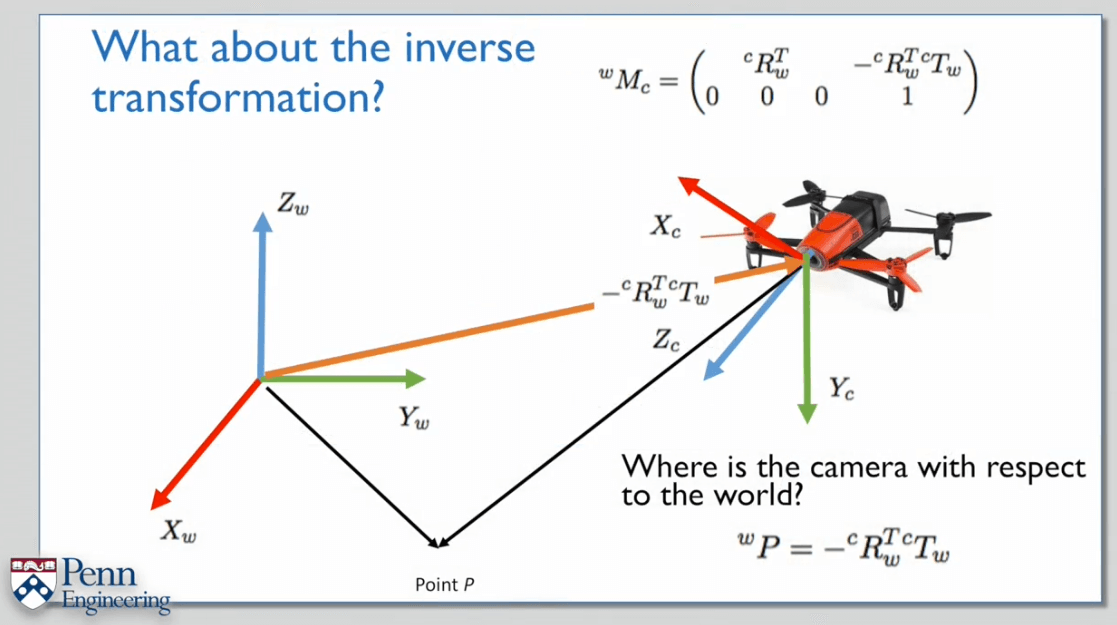
另一种理解变换的方式是采用一系列的运动。
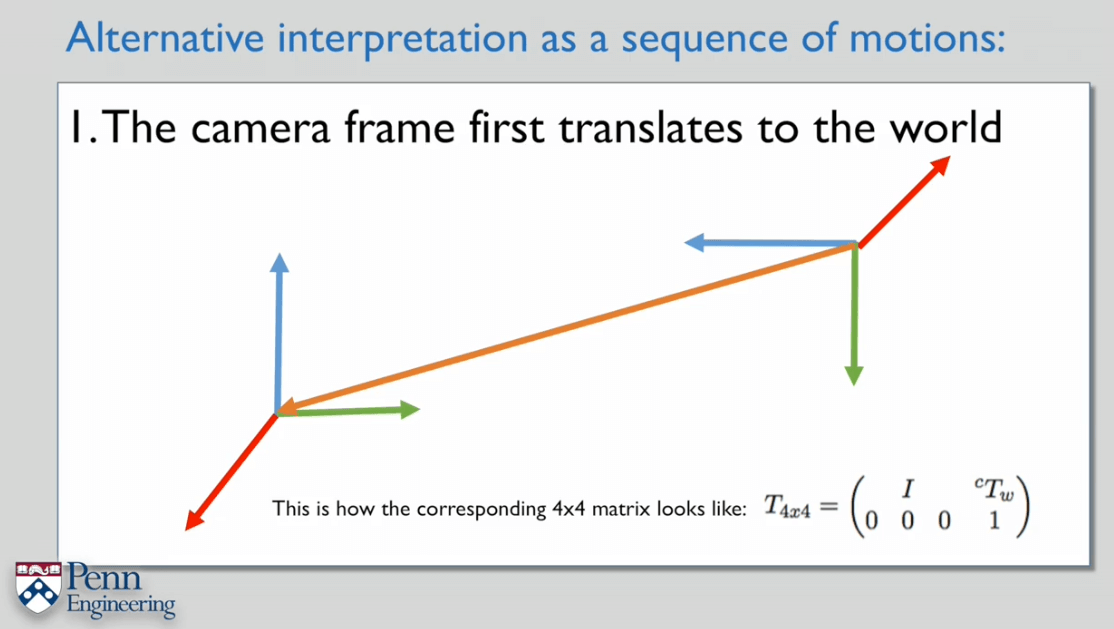
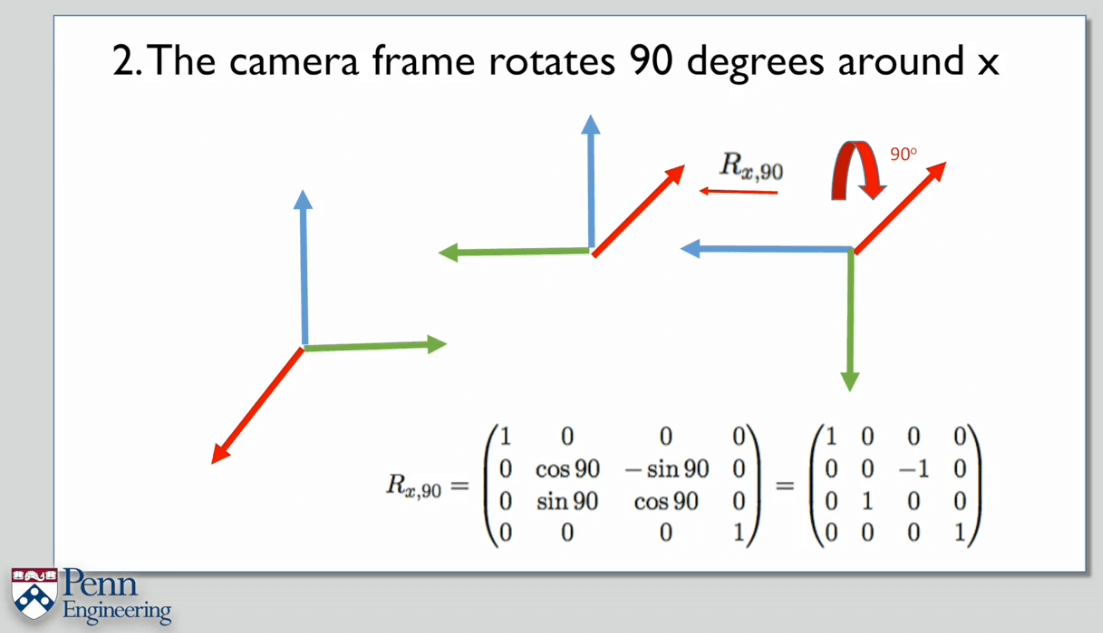注意旋转正负号是顺时针旋转为正，逆时针为负。
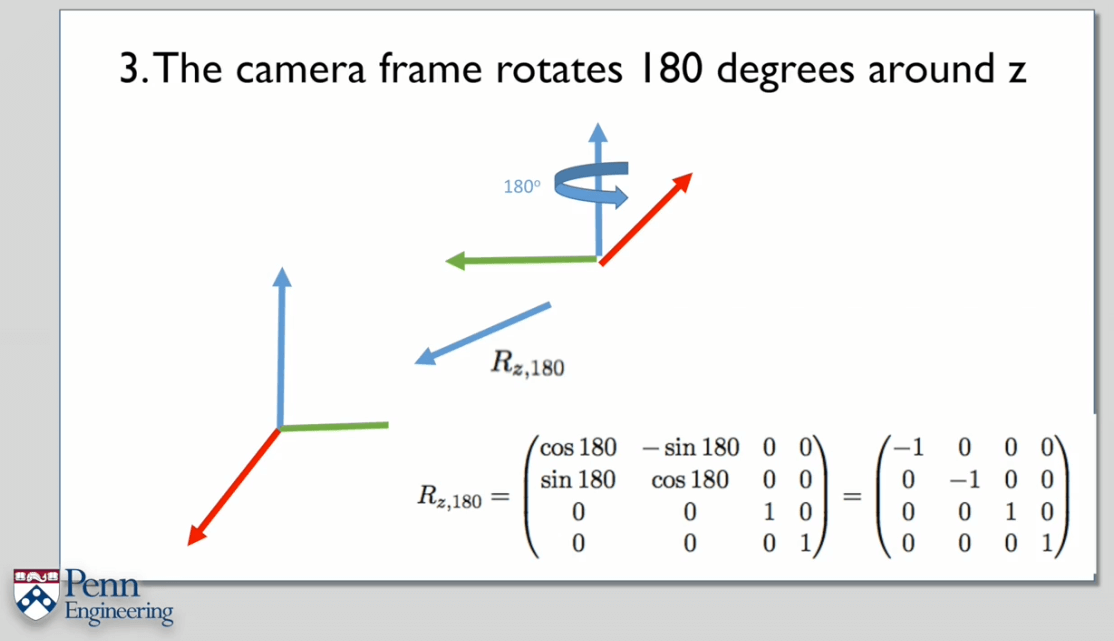
变换时一般先平移，后旋转。注意构成变换矩阵时的法则是总是参考最近一次变换的坐标系并且将旋转右乘。
7.Pinhole Camera Model
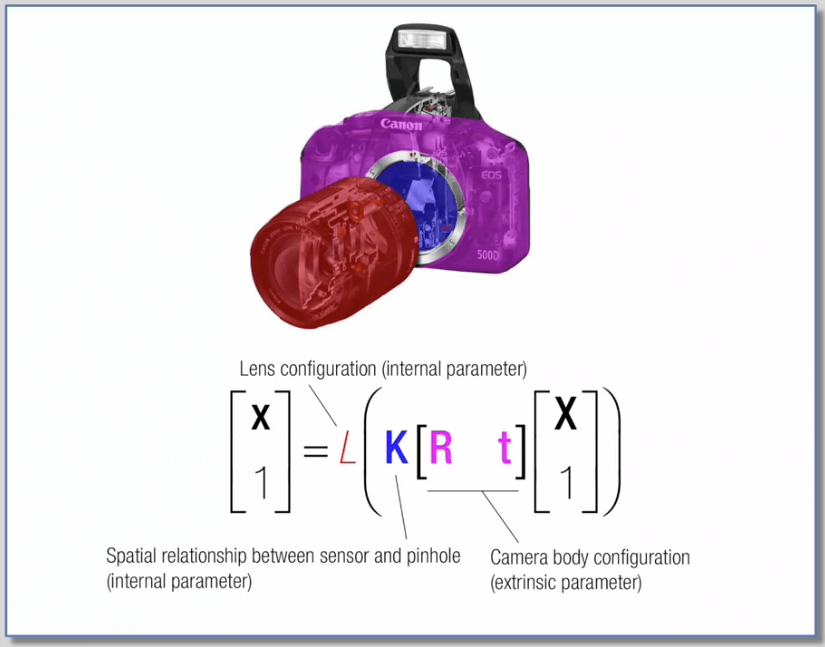
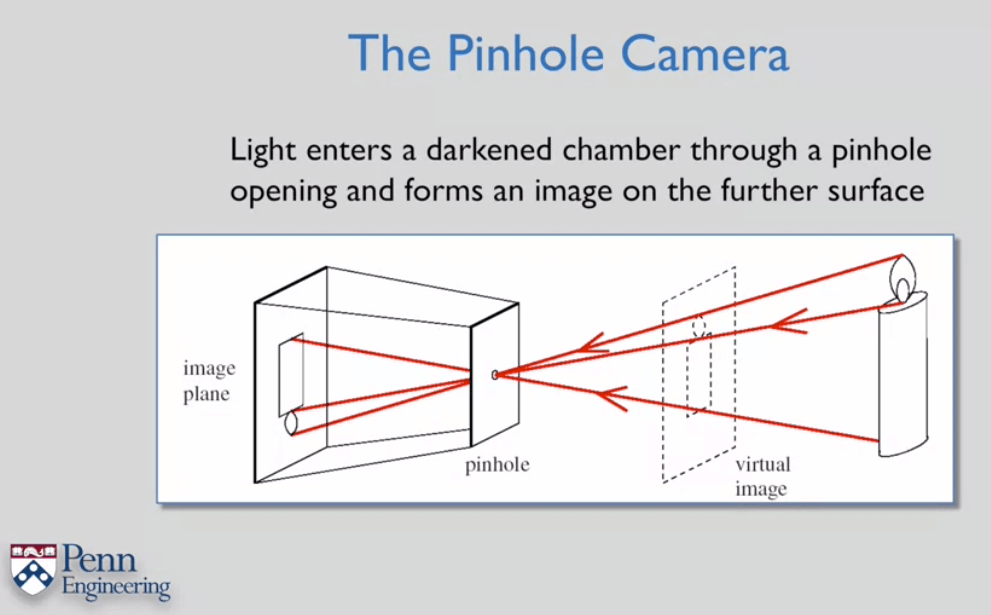
相机坐标系的定义：以相机光心为原点，水平向右为x轴，垂直向下为y轴，满足右手定则，z轴指向相机正前方。从上面的式子也可以看出：
- (1)被摄物体在像面的大小与其距离坐标原点的距离Z有关，近大远小；
- (2)在外界条件不变的情况下，f越大(像面离光心越远)，在像平面上成的像越大；
- (3)由于像面大小是固定的，所以当增大f时，像面所反应的视野会变小，反之会增大。
估计相机光心的办法
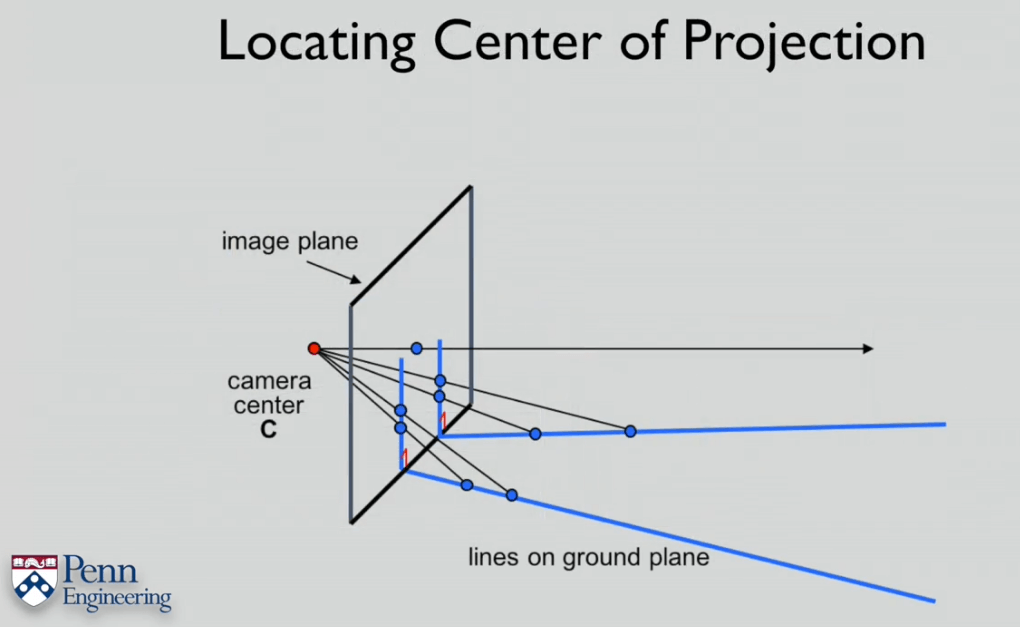
8.Focal Length and Dolly Zoom Effect
改变焦距的过程又被称为Zooming，长焦距可以起到对物体放大的作用，可以造成将远处物体拉近的感觉。但正如上面所说，其视角也会变小。注意和对焦的过程区分开。对焦是指焦距本身不改变，通过改变像面到相机光心的距离来调整成像，使得由某点发出的经过和不经过光心的光线在像面上精确汇聚于一点。在第一部分的动图已经演示了对焦的过程。
Dolly Zoom Effect
沿Z轴改变相机的位置(如拉远)并同时增大焦距，可以产生Dolly Zoom效果。可以使近处的物体看起来大小不变而远处的物体看起来被放大和拉近了。
其原理也很简单，为了方便，以y方向作为介绍。假设某个参考时刻的焦距是\(f_{ref}\)、此时相机在z轴的距离是\(Z_{ref}\)。在相机沿z轴移动了pos(规定远离物体为负，靠近物体为正)以后，我们要保持的是其成像的高度不变，所以有：
由于相机只沿z轴运动，所以目标点的X、Y坐标都不变，对右边两个等式同时约去Y，即可得到f’与pos的关系，即为保证高度不变，在移动了pos后，焦距应该变为f’。
9.Intrinsic Camera Parameter
将相机坐标系下的坐标转换为像平面上的坐标
将像平面坐标转换为像素坐标
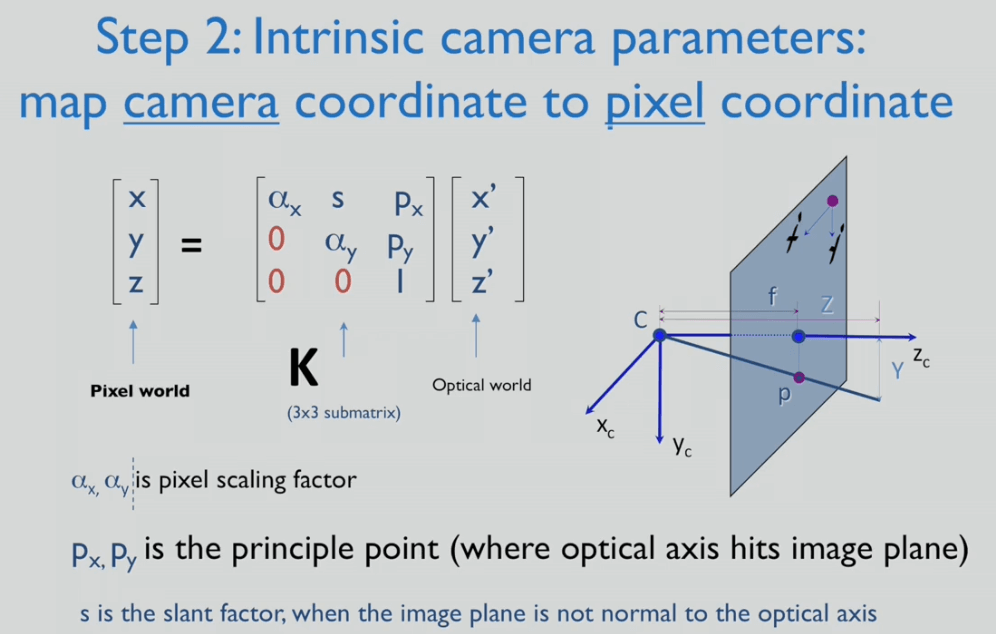
前面那部分3×3的矩阵叫做Calibration Matrix，简称K Matrix。
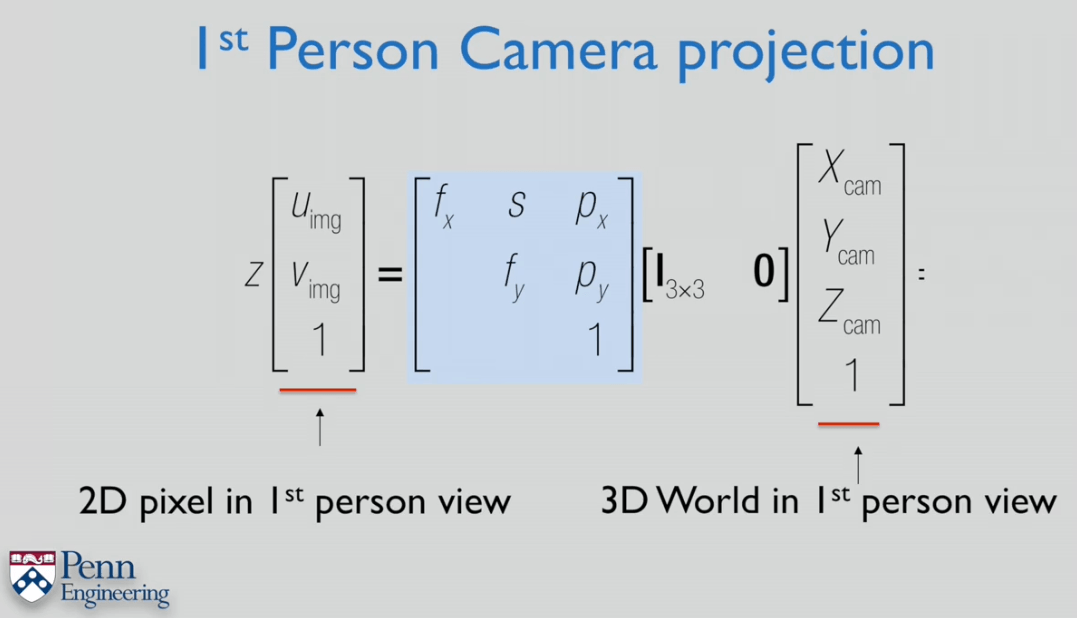一个由3D相机坐标系下的坐标转换到2D像素坐标的过程如上图所示。可以将相机坐标系下的坐标写成非齐次形式，简化形式如下：
Calibration Matrix中个变量的含义如下：
10.3D World to First Person Transformation
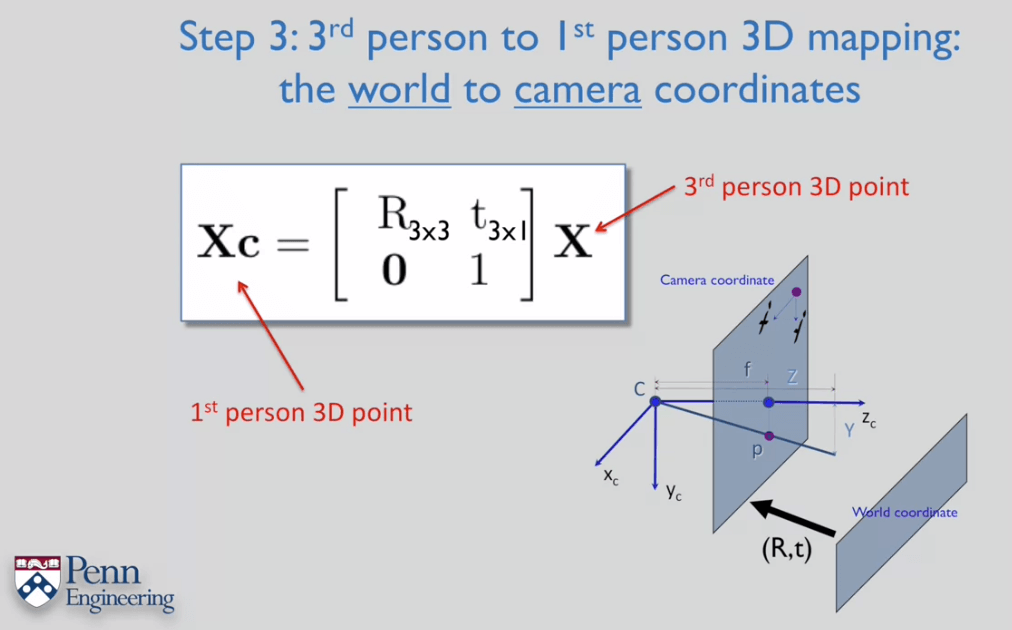
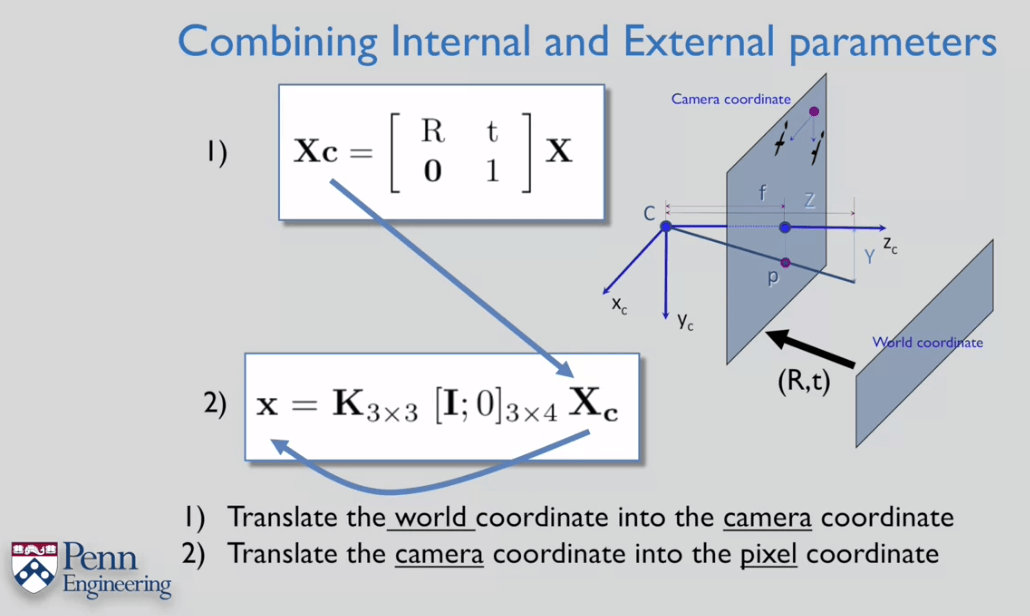
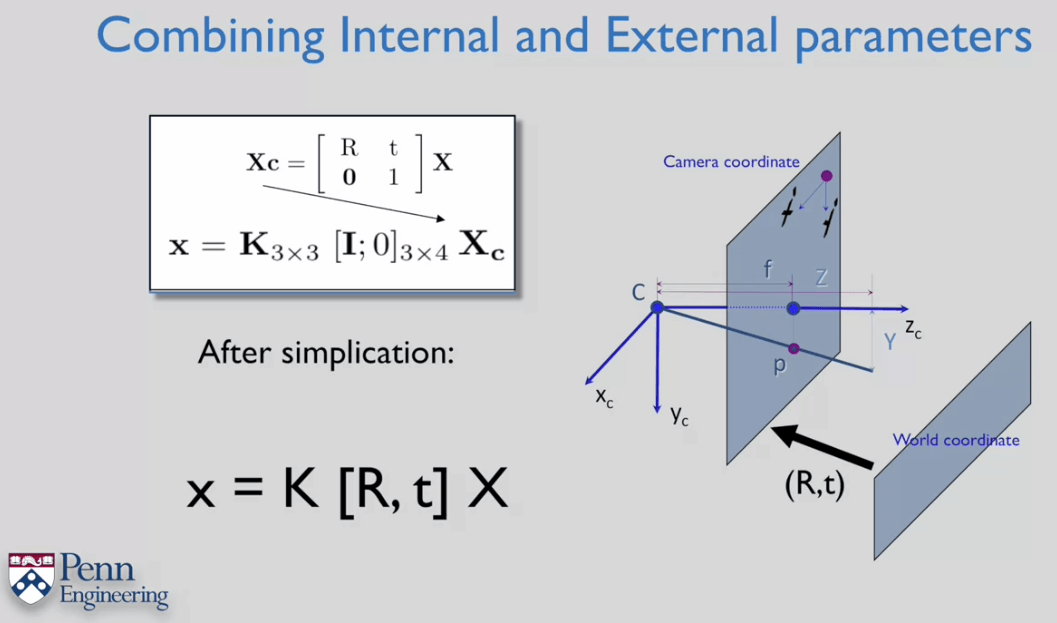
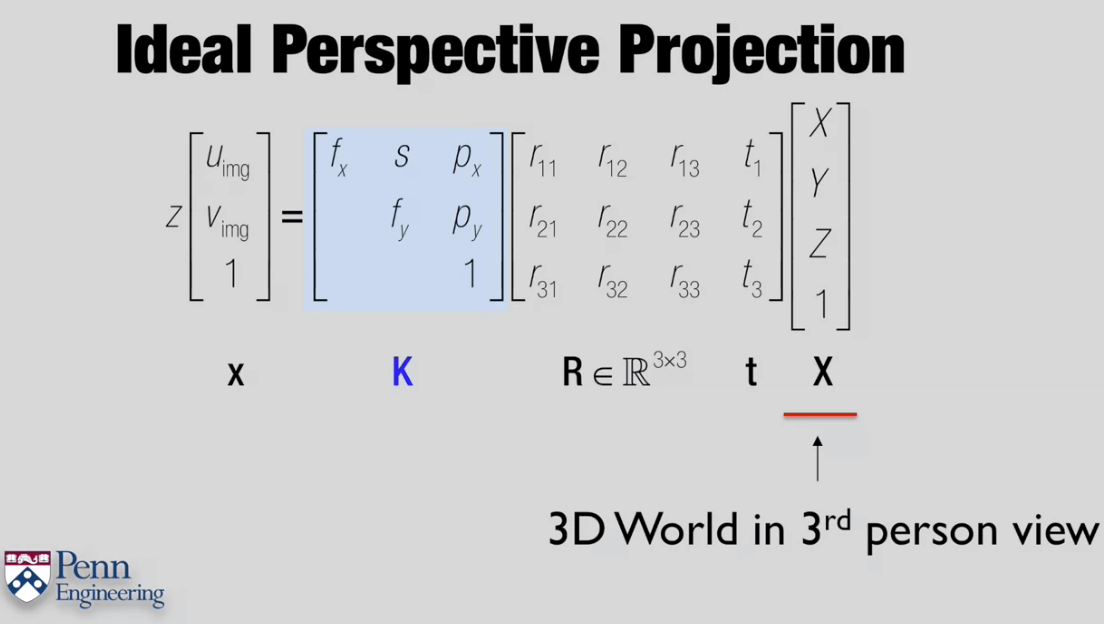
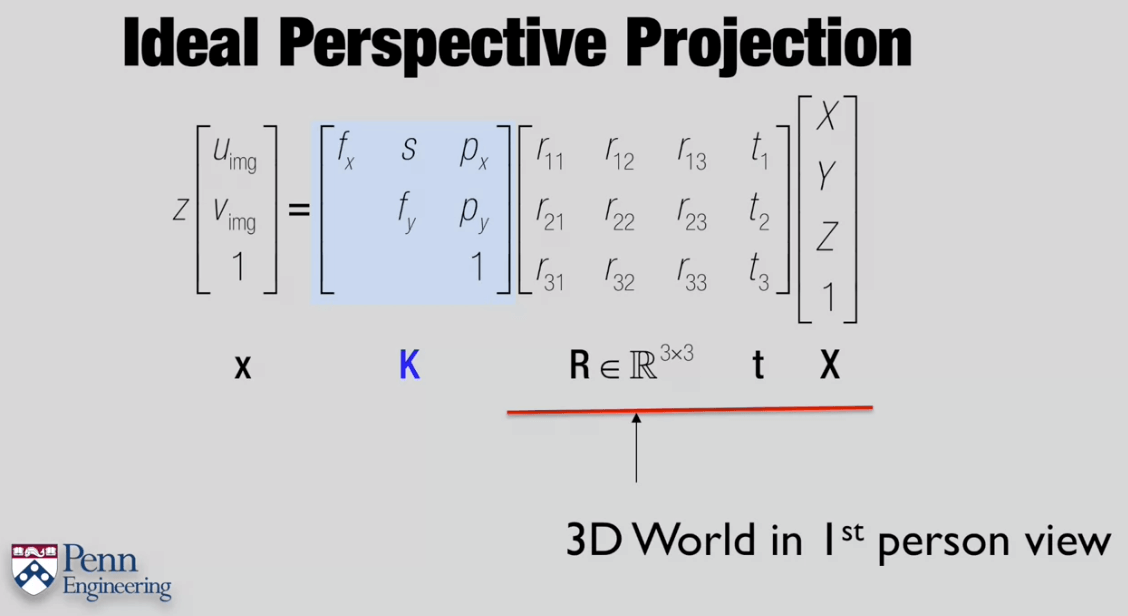
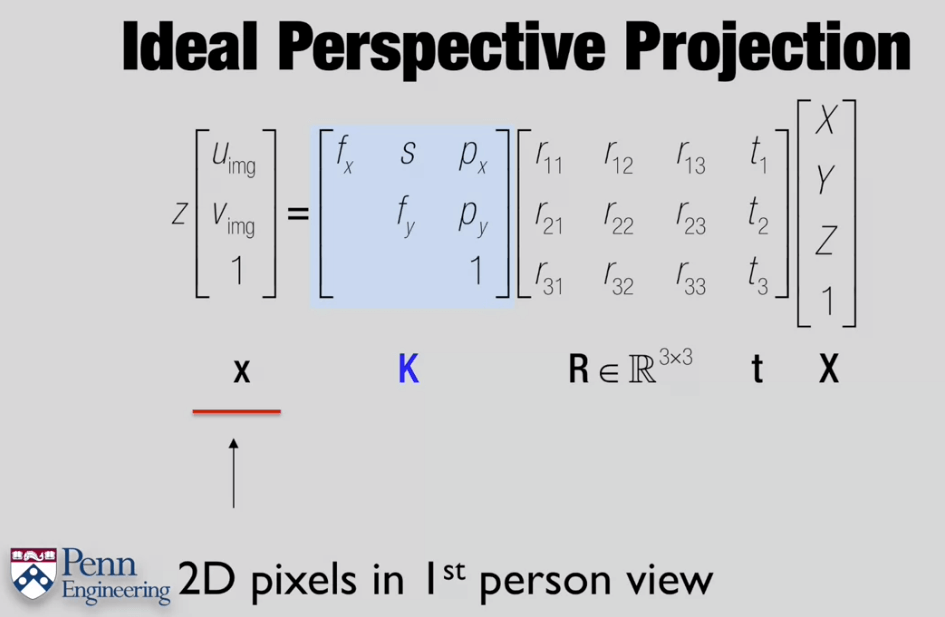
相机的R、t称为外参，描述了相机的位姿，用于将一个在第三人称坐标系(如世界坐标系)下的三维点转换到第一人称坐标系(相机坐标系)下的三维点。K矩阵是一个3×3的矩阵，用于将一个在第一人称3D坐标系(相机坐标系)下的三维点变换到第一人称2D坐标系(像素坐标系)下的二维点。
以下有两种特殊情况。
平面-单应变换
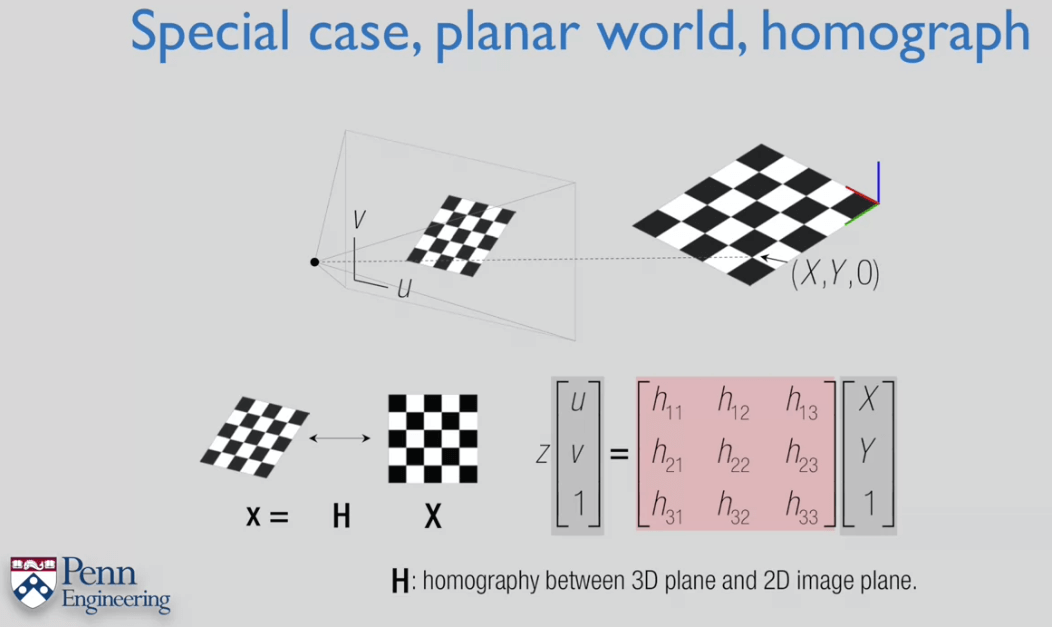
我们有选择第三人称坐标系的自由，而且这些点又都位于同一平面，所以我们可以找到这样一个第三人称坐标系：X、Y在这个平面之中，Z垂直于该平面。这样在物体上的所有点的Z分量都为0，记为(X,Y,0)，齐次写法为(X,Y,0,1)。然后通过旋转矩阵R、平移t，以及Calibration矩阵K，就可以获得它在图像上的像素坐标。这个思想在做相机标定的时候就有用到，认为棋盘格坐标的z分量为0，然后棋盘格的坐标就是数格子然后乘以每个格子的真实长度(mm)。
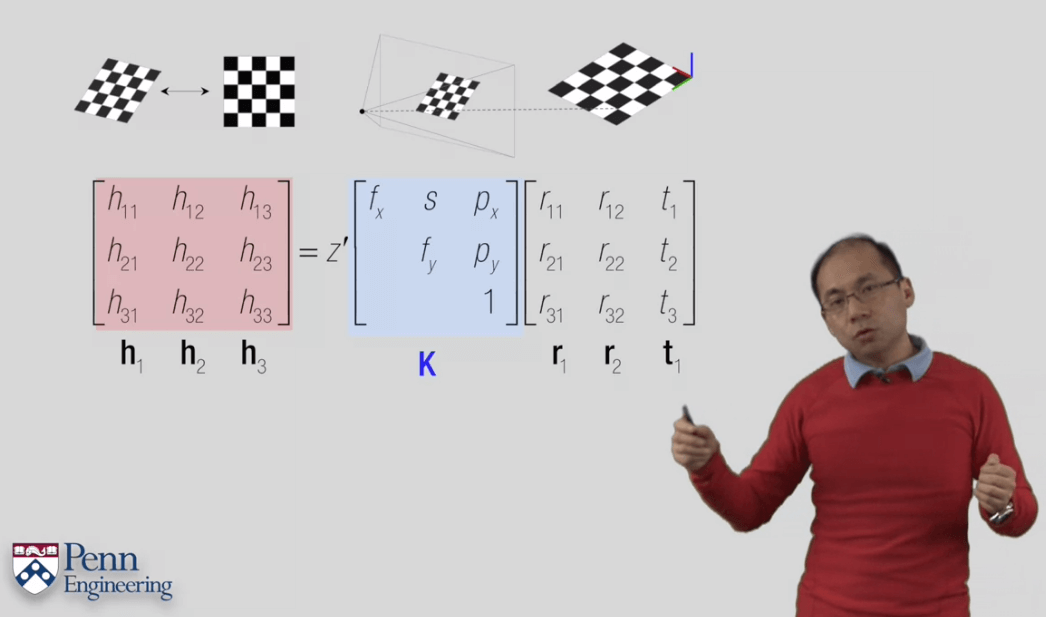
注意这里旋转并没有Z分量。因为平面上的所有点分量为0，和旋转矩阵相乘时，旋转矩阵的第三列全为0,所以去掉了。
纯旋转
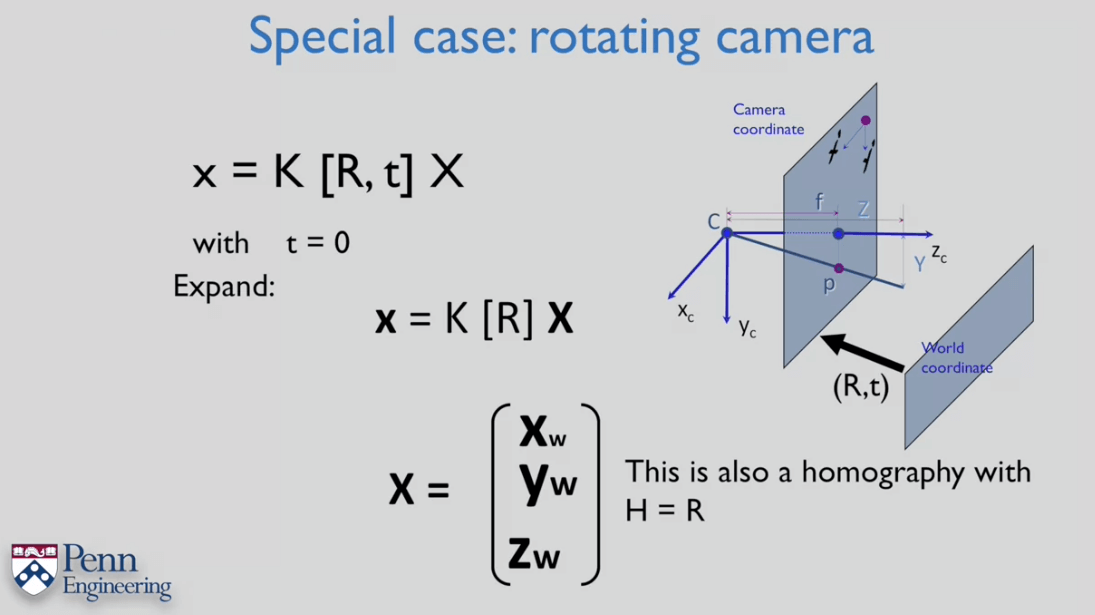在这种情况下，没有运动视差，物体之间没有相对角度变化，因此无法感知三维世界的状态。要想感知三维，相机中心必须要有所移动。
11.How to Compute Intrinsics from Vanishing Points
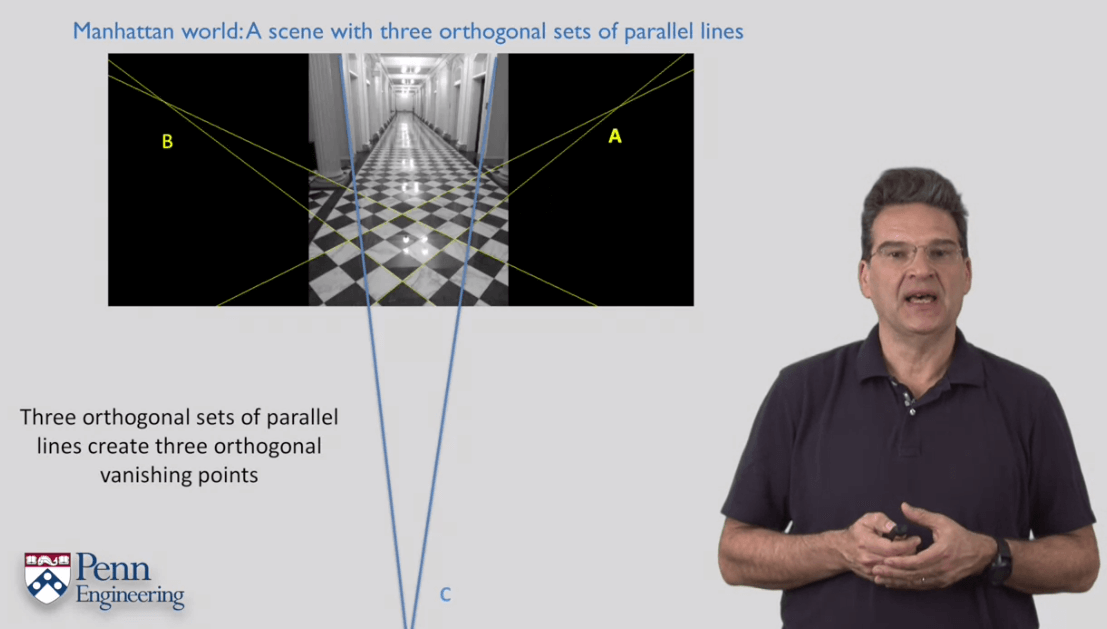
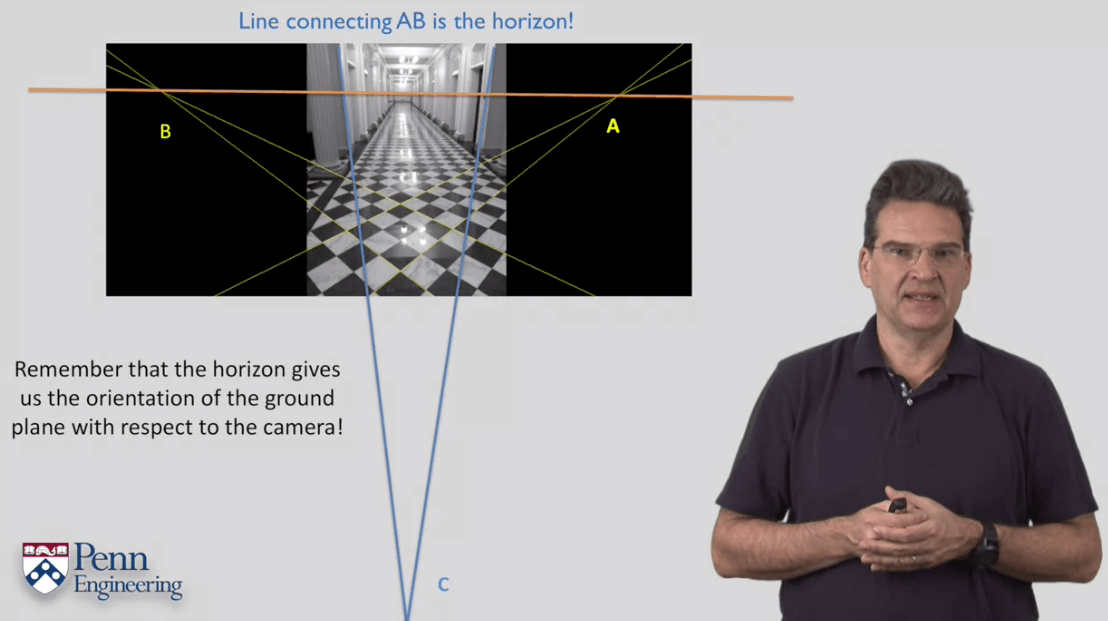
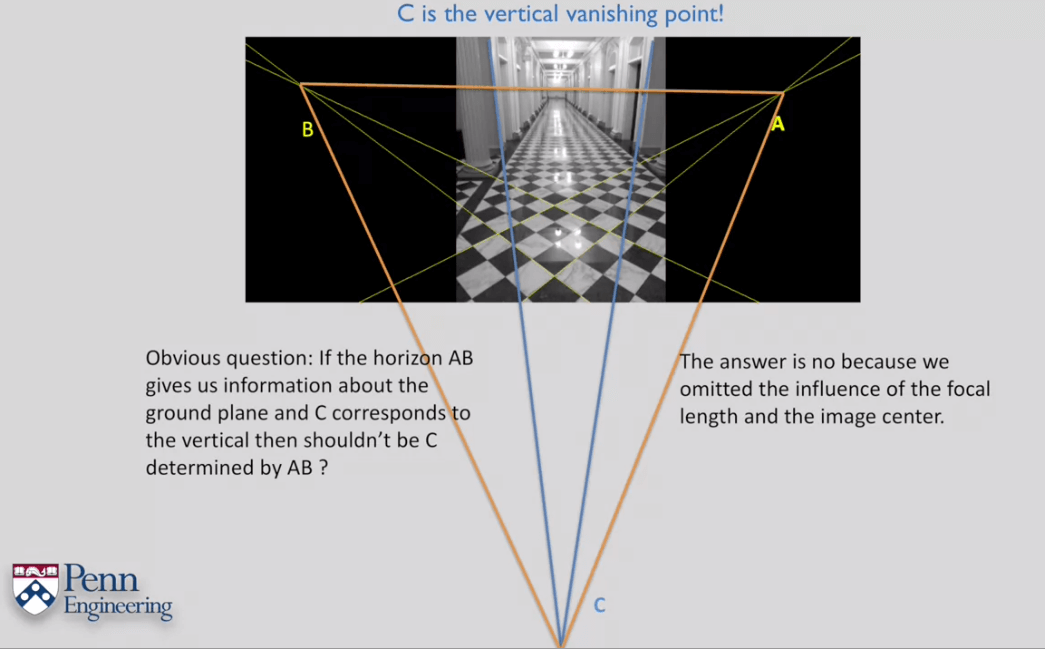
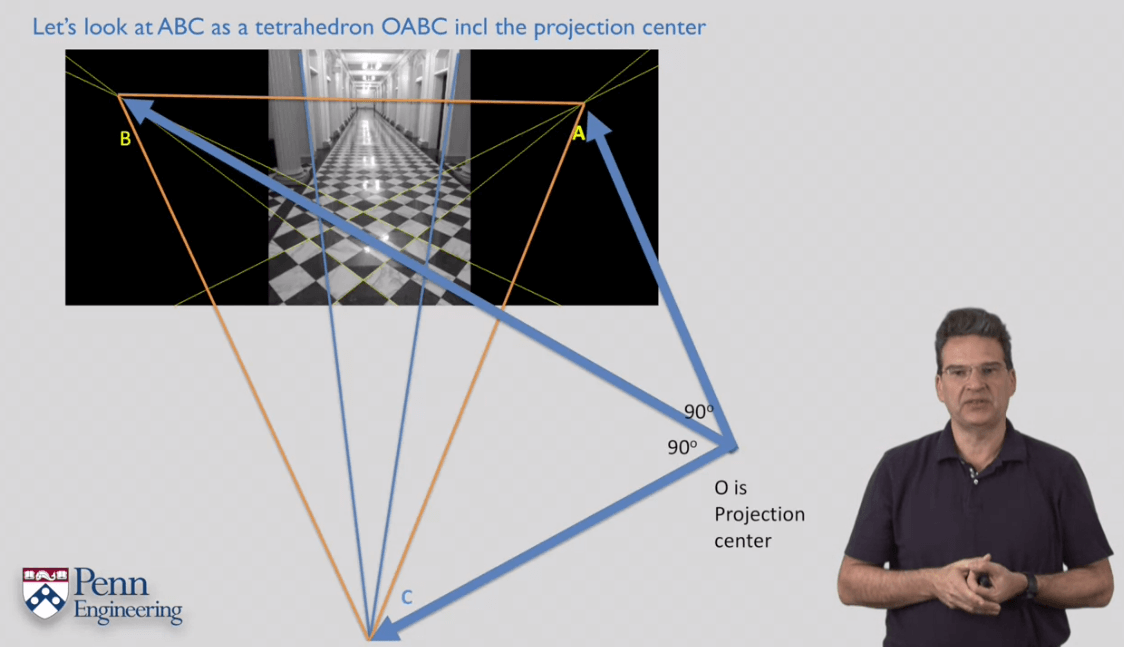
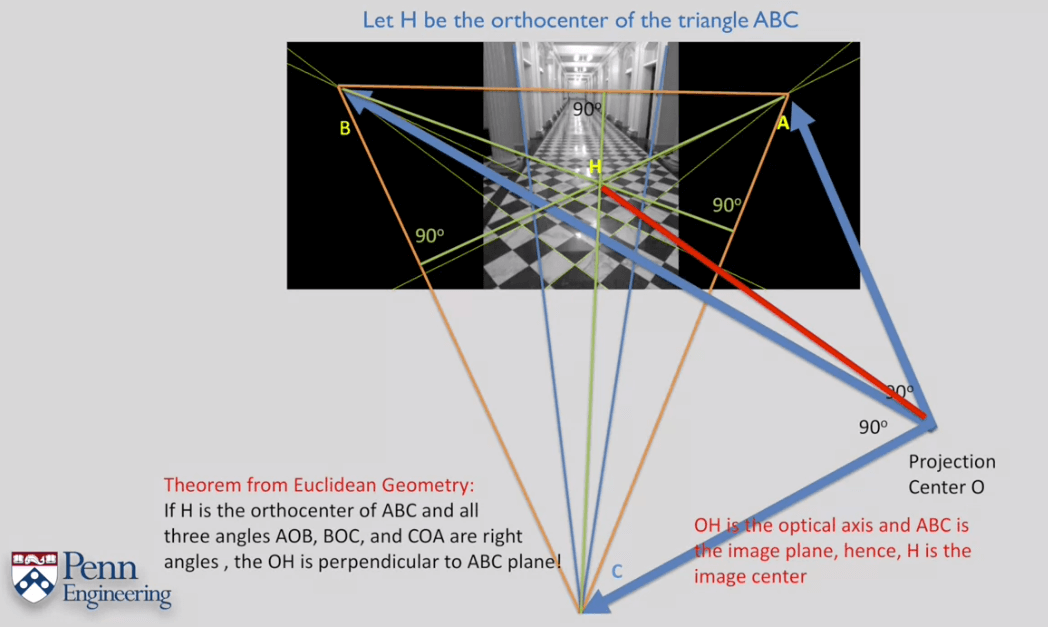
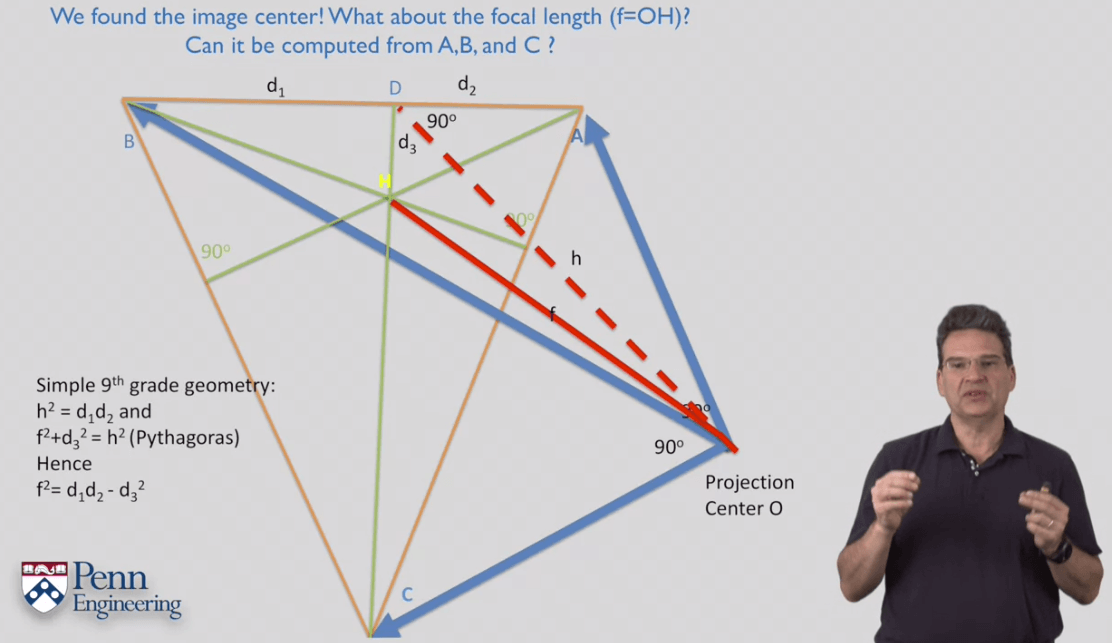
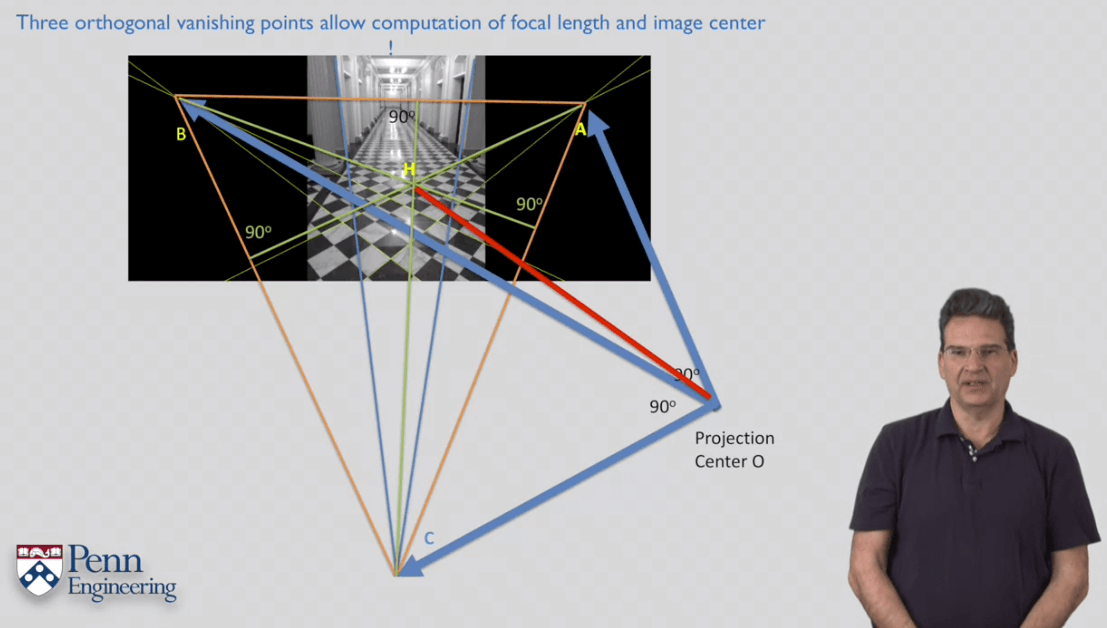
12.Camera Calibration
3×4的投影矩阵P。
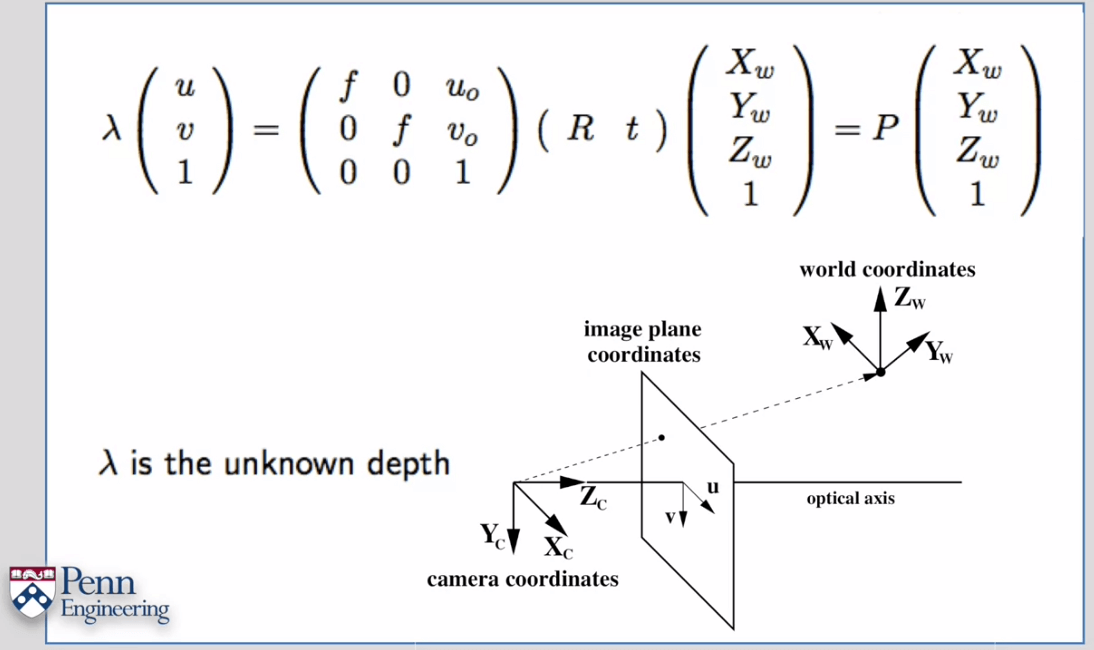
一个Calibration的过程用于估计内参，包括焦距f、主点坐标以及畸变参数。
在Matlab中也有calib_gui模块可以方便地用于校正。
本文作者原创,未经许可不得转载,谢谢配合
