1.Visual Features
(1)特征的用途
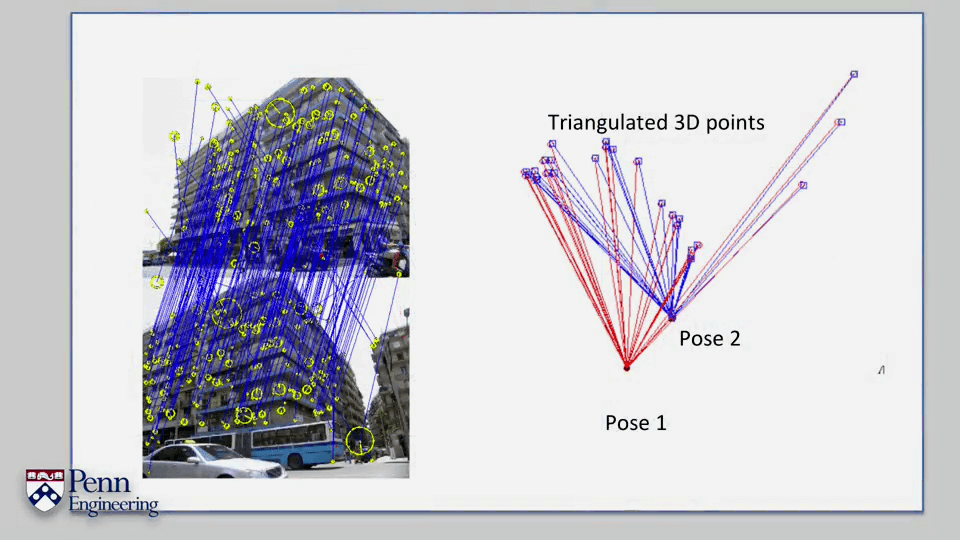我们需要找到影像中的一些特殊的点进而找到影像之间的变换关系，并以此来进行定位(localization)或者三维重建(reconstruction)。除此之外，正确的找到影像中的特征还可以用于场景识别(place recognition)以及其它影像检索(retrieval)等任务。
(2)特征应该具备的性质
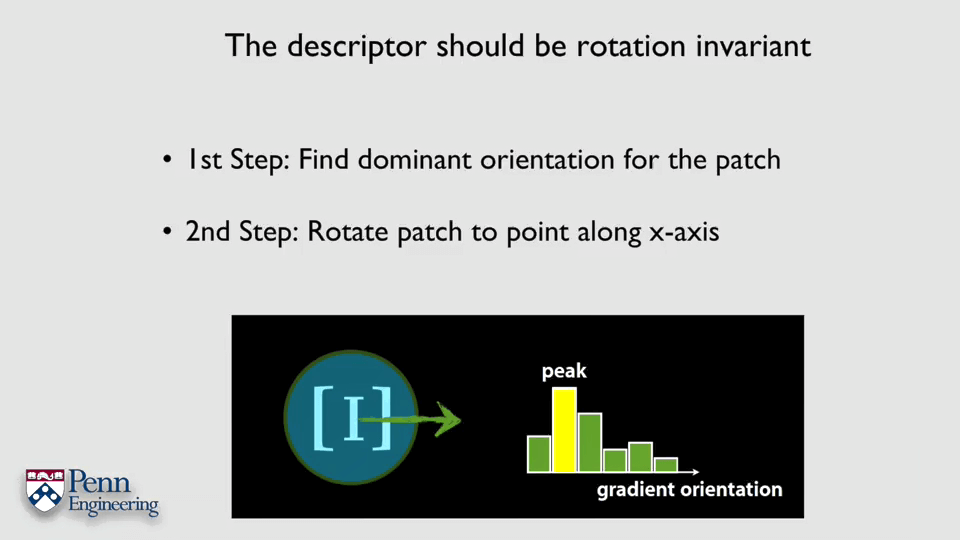
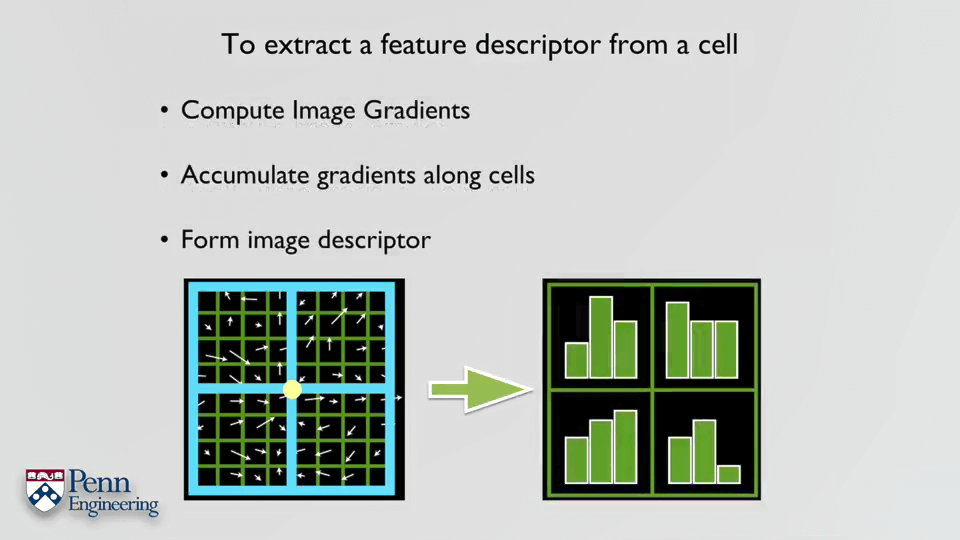
我们认为一个特征应该具备检测的可重复性(Detection Repeatability)或者说在不同影像中的检测不变性(Detection Invariance)。与之对应的，为了能匹配正确的点对，我们也希望特征具有描述不变性(Descriptor Invariance)。
(3)SIFT
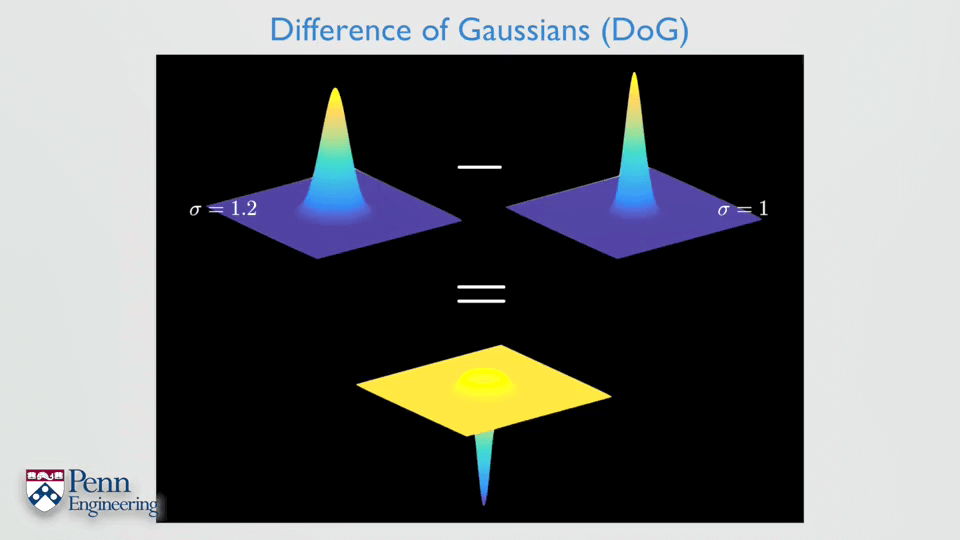
SIFT尺度空间的建立过程：将原始影像与不同参数的高斯核做卷积，即可得到不同模糊程度的影像。
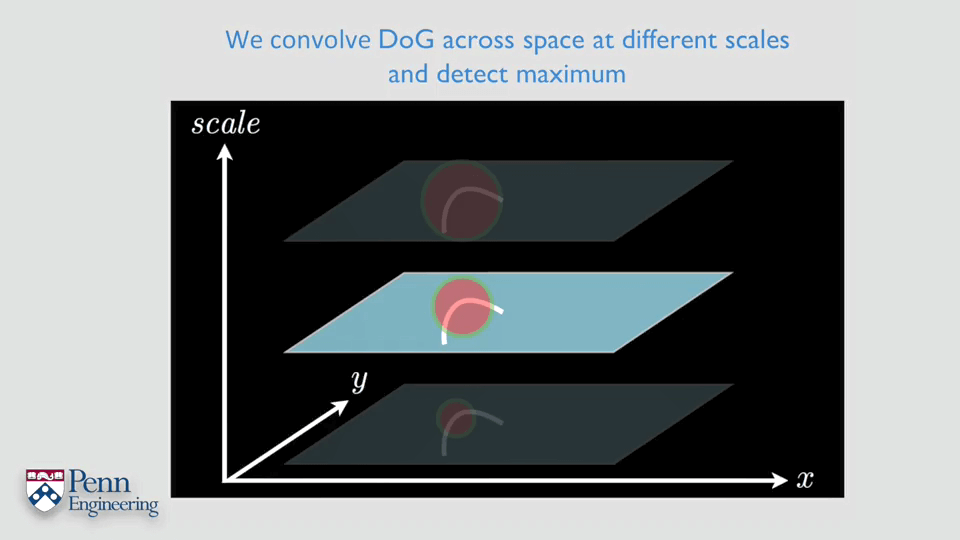
影像金字塔的建立过程。每当高斯核的σ变为原来的2倍时，对影像进行降采样。
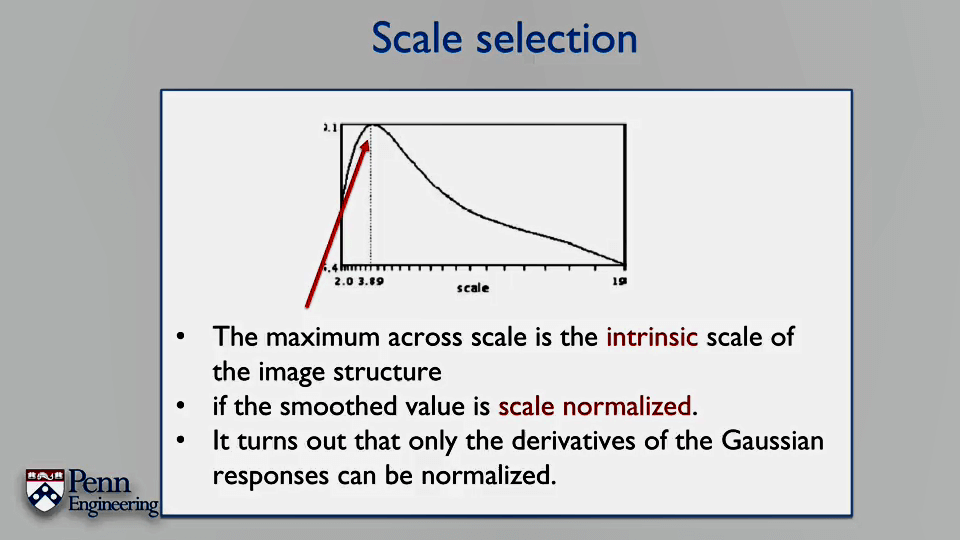
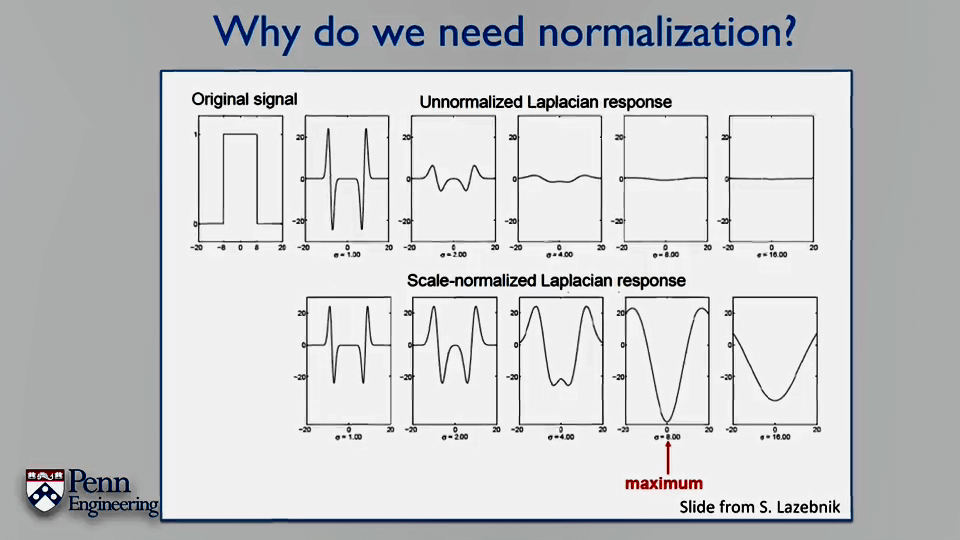
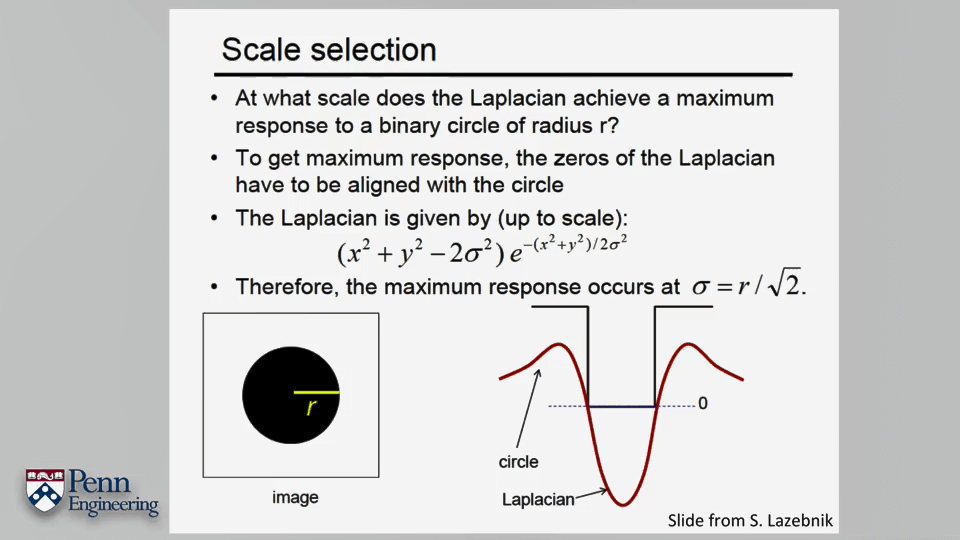
2.SVD与Least Square Problem
(1)SVD
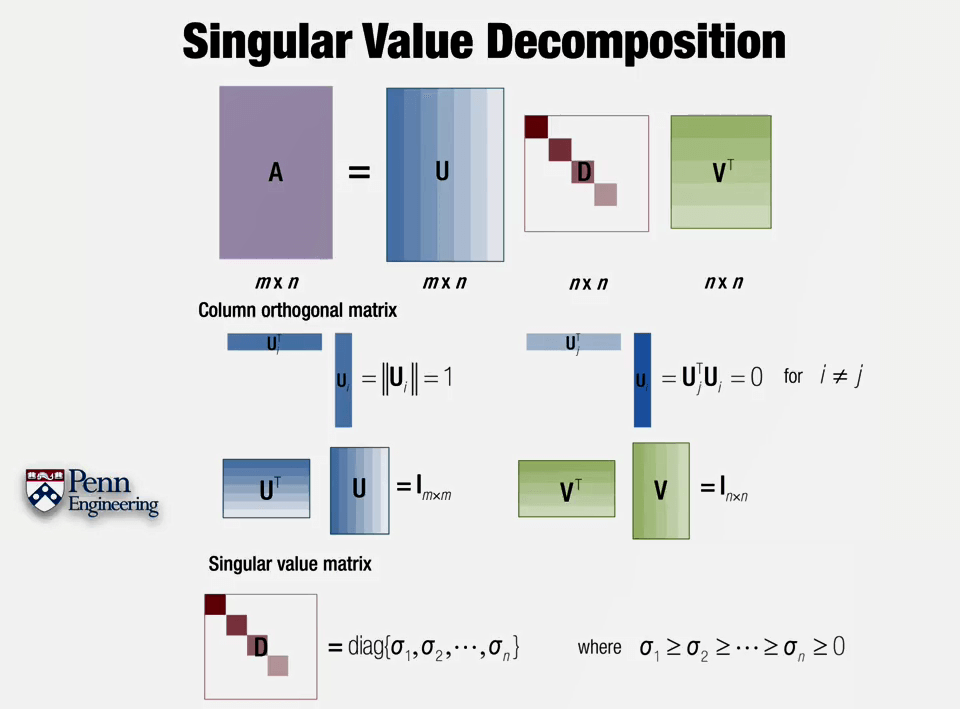Singular Value Decomposition。分解得到的U矩阵是一个列正交矩阵，取其任意一列(n×1)将它的转置(1×n)与其相乘，得到的结果为1。也就是说U的每一列的模长为1。取U的第i列(n×1)与第j列的转置(1×n)相乘结果为0，也就是说U的每一列都互相垂直。VT有和U类似的性质，每一行都互相垂直，每一行模长为1。UT和U相乘、VT和V相乘结果都是单位阵。而对于D，对角线元素即为奇异值，且依次递减，最小为0。奇异值其实反映了U的某列对于A的贡献(这也就是为什么最小为0的原因)，如果奇异值非常大，则表示贡献非常大，如果接近于0，则表示U的这一列几乎没有什么贡献，去掉也没什么关系。这就是主成分分析了。可以注意到，如果A是m×n，那么U和A大小相同为m×n，D和VT都是n×n。
这里需要注意的是SVD分解并不是只有上面说的这一种形式。上面这种形式是行>列的情况下，使奇异矩阵为方阵时的分解结果。更多有关内容可以参考这篇博客的总结。
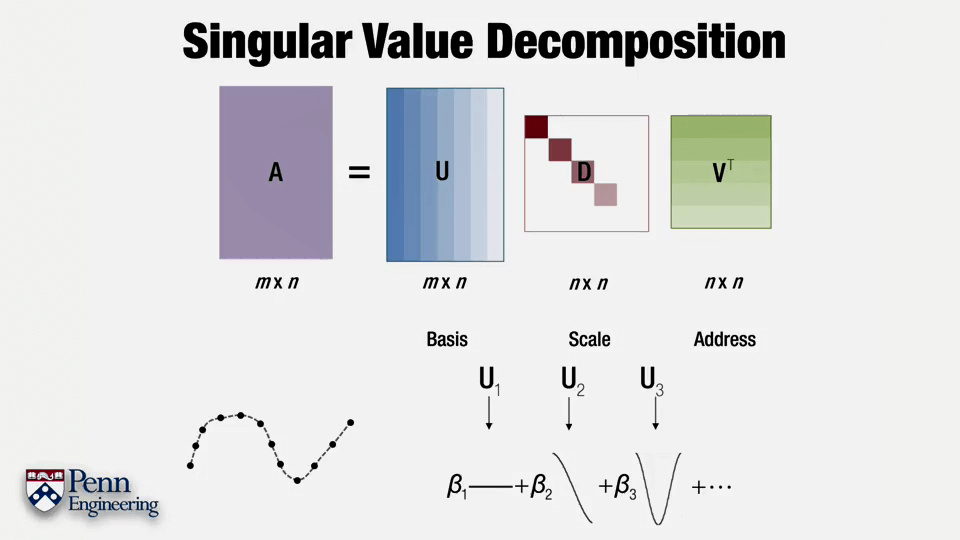理解SVD的思路可以把SVD当作是Basis+transformed Address。如果把A当作是一个曲线，U可以理解为一些表达曲线的基本形状，VT表示了这些形状所在的不同位置，D则表示了这些形状的缩放大小。最后通过它们就可以恢复出原始曲线的样子。如下是利用SVD恢复某张图像的效果。
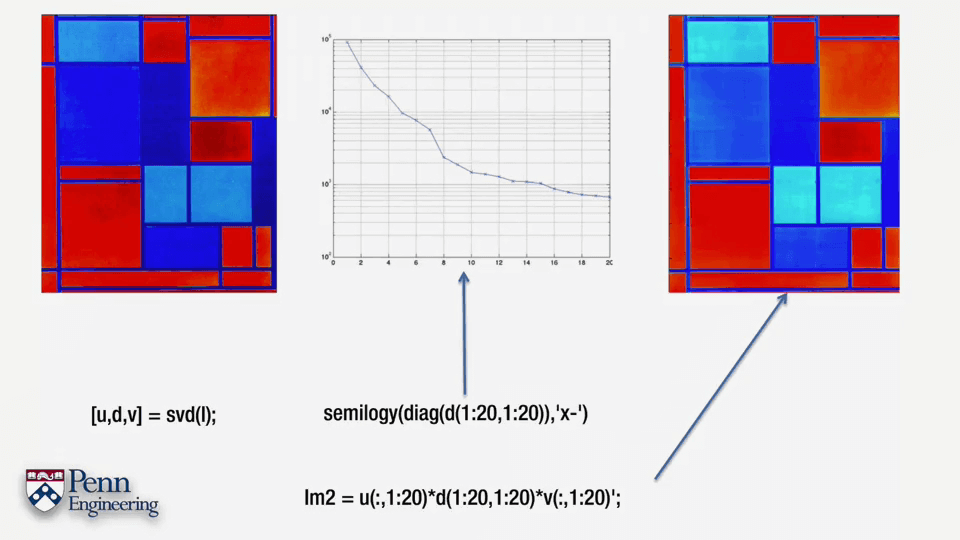可以看出，只需要取U的前20列，即可以几乎完全一致地恢复了影像。所以SVD是简化矩阵、清洗数据、压缩数据、去除冗余数据的好办法。
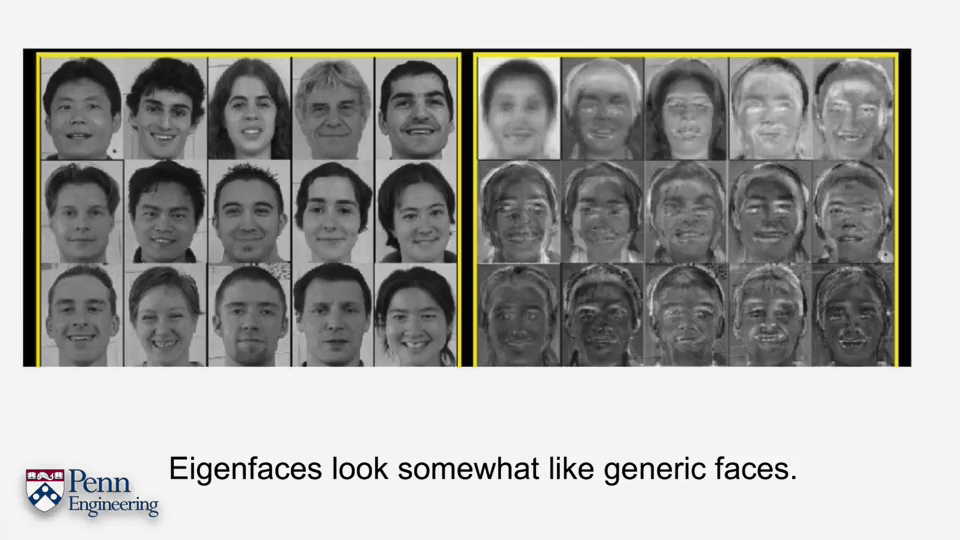
我们可以把一张影像认为是一个长长的向量，然后将很多张影像的列向量放在一起，这样就可以得到了一个巨大的矩阵。对这个矩阵进行SVD分解，即可得到影像的一些共性表达和特征。例如对人脸进行分析。
借助SVD分解，我们也可以得到矩阵A的秩(Rank)，即等于奇异值矩阵D中非零对角线元素的个数。根据这个性质可以得到SVD分解的另一个用途是，利用SVD分解可以获得指定秩的矩阵。先将矩阵A进行分解，然后取奇异矩阵中前m个非零元素，重新组成矩阵，这个重新组成的矩阵的秩即为m。
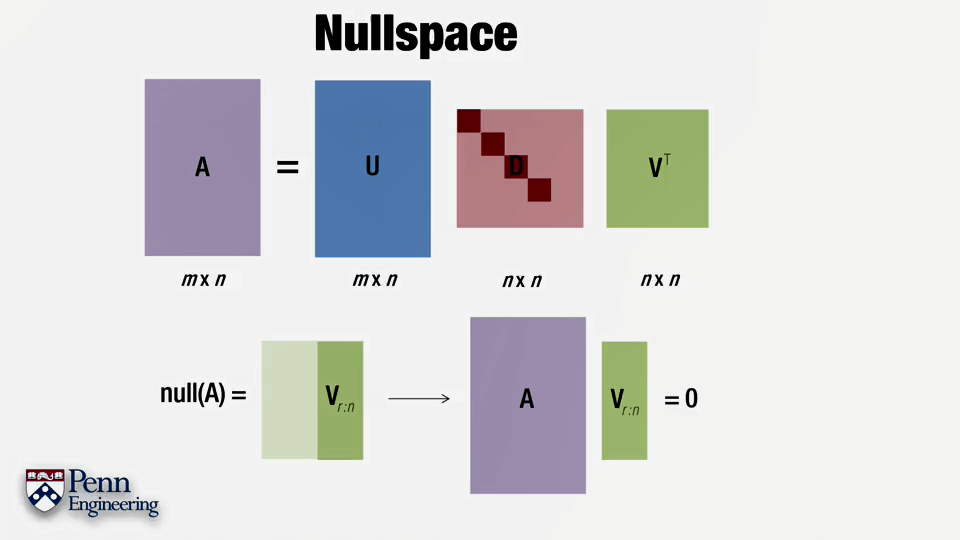零空间。
一个SVD分解的简单例子。
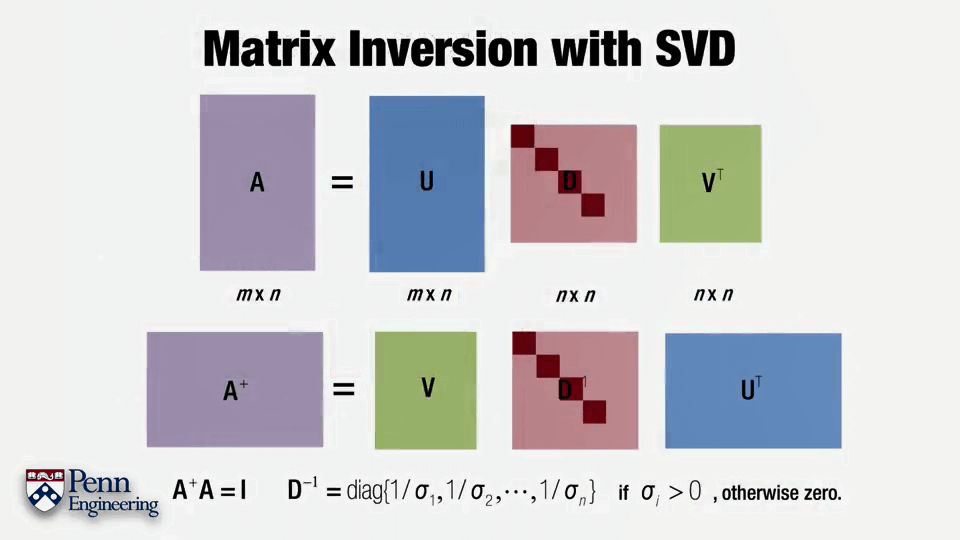SVD分解的另一个用途是对矩阵求逆，如上图所示。A-1=VD-1UT。
(2)Least Square Problem
最小二乘问题的两种形式：齐次与非齐次。
非齐次
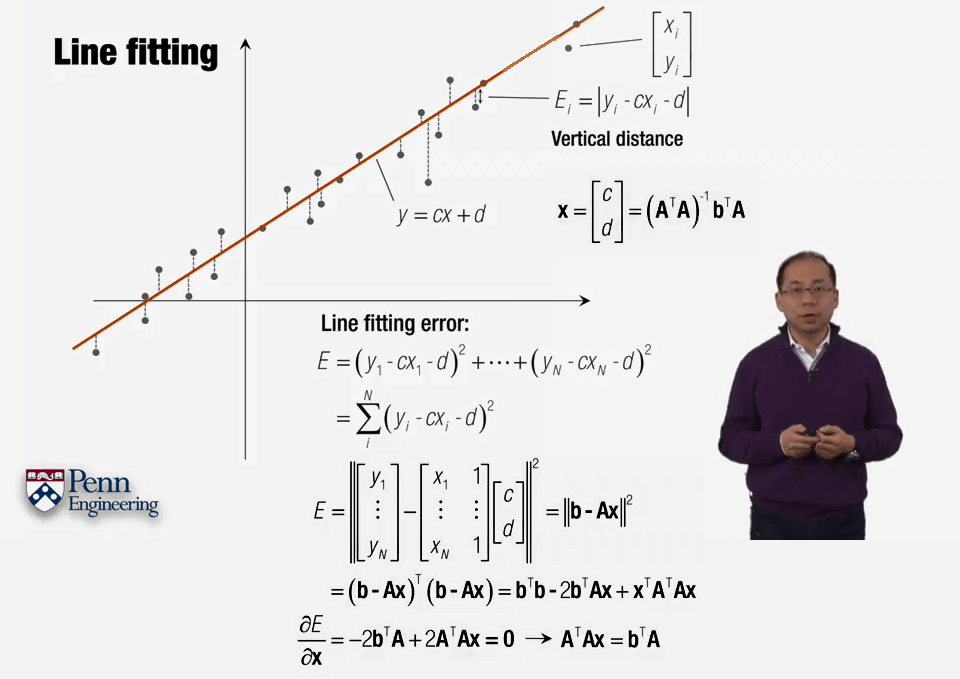直线拟合。这里(ATA)-1被称为A的伪逆。因为根据可逆性质，可逆矩阵一定为方阵，而这里A并不是为方阵。所以称为A的伪逆。
非齐次线性方程组不同情况下的解：欠定、适定、超定。
齐次
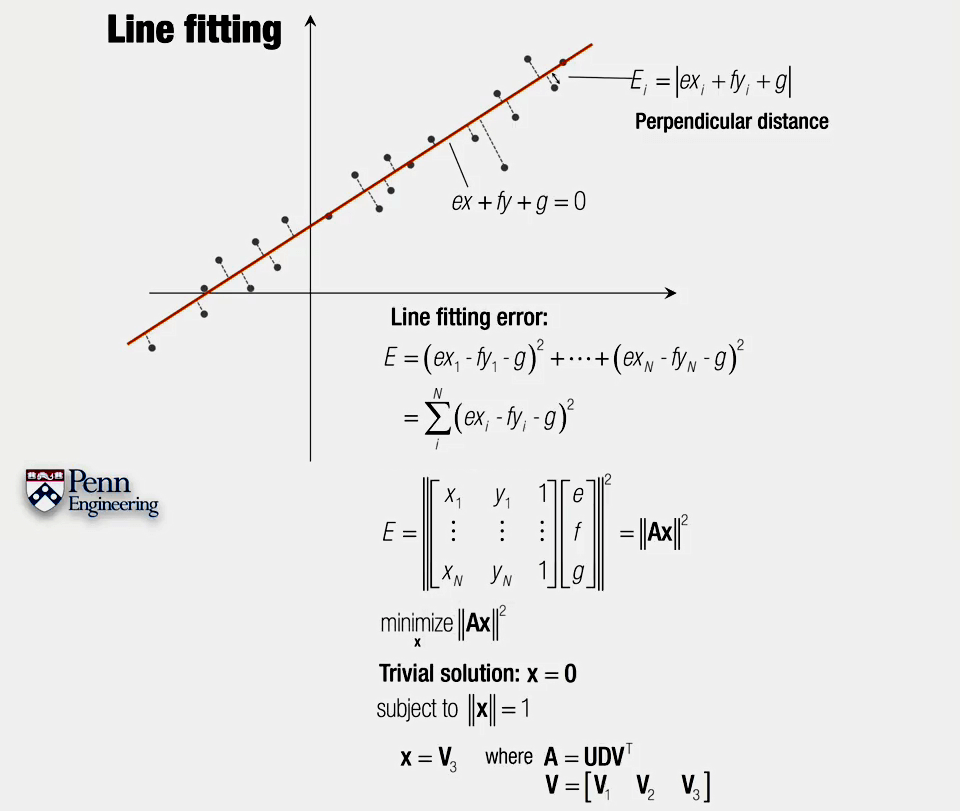齐次下的直线拟合。这里采用了另一种误差度量方式。注意最后方程组的解是V的最后一列。但SVD分解直接中得到的是VT，因此对应也就是VT的最后一行。
齐次线性方程组不同情况下的解：欠定、适定、超定。
3.RANSAC
(1)用途
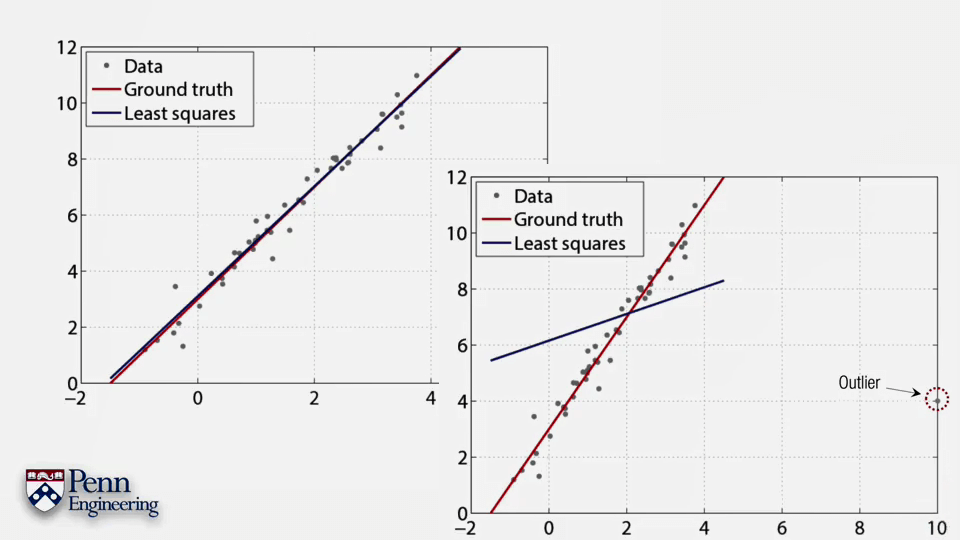在上面提到了，采用Least Square+SVD的方法可以十分有效地解决问题。Least Square用于构造方程组，SVD则用于解方程组。但这里有个问题，最小二乘方法虽然很棒，但是对离群点十分敏感，可能个别离群点会导致解的不稳定，如上图所示。因此在应用最小二乘之前应该需要采用RANSAC来去除离群点。Random Sample Consensus，随机采样一致性。是去除离群点(Outlier)的好办法。
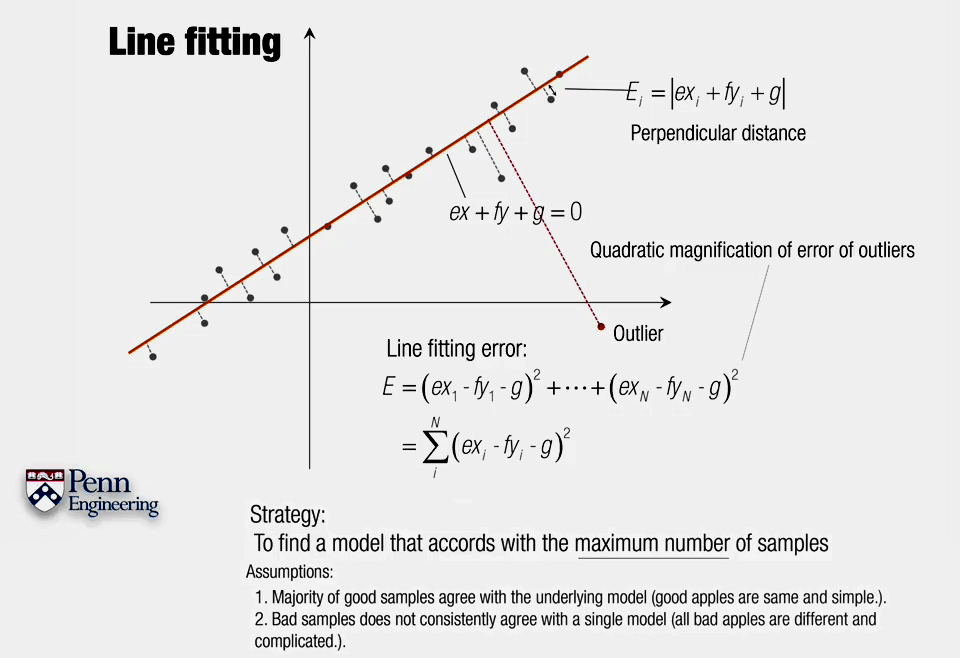为了去除离群点，我们使用这样的策略：找到一个适合绝大多数样本的模型，对于离群点则选择忽略。
(2)具体步骤
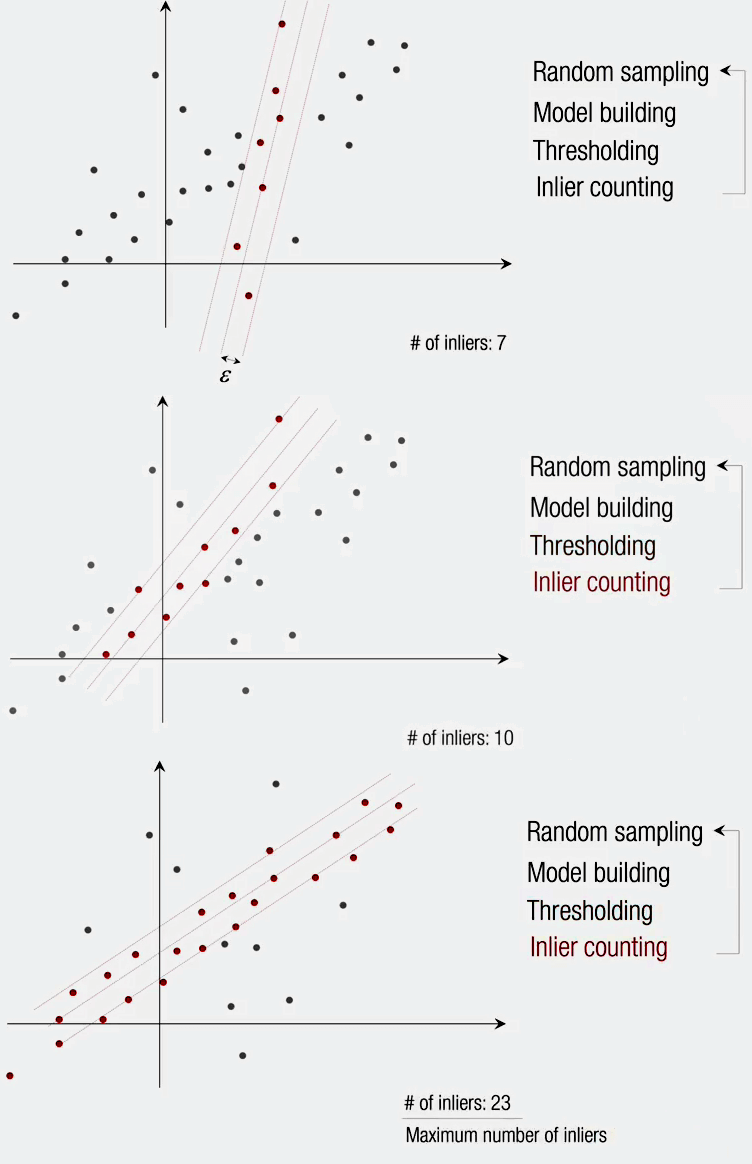
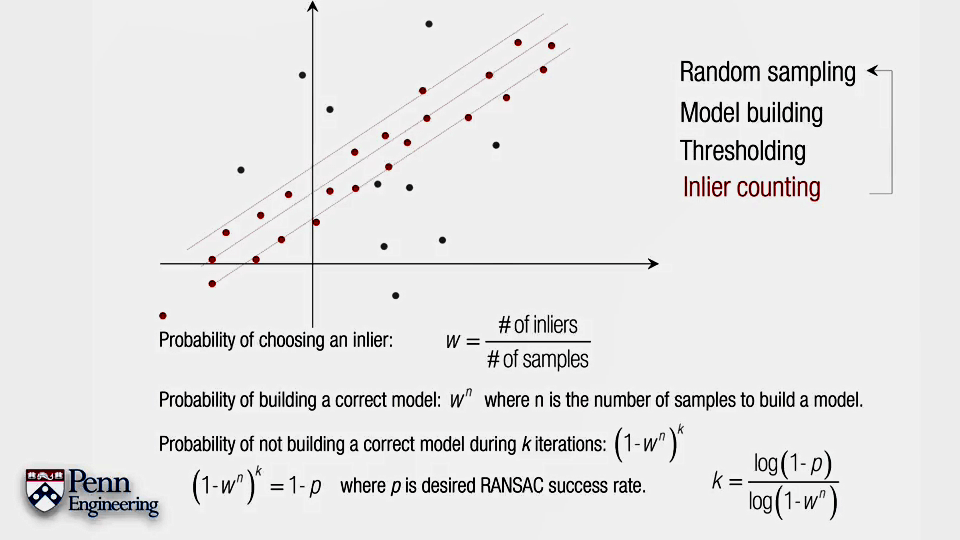
本文作者原创,未经许可不得转载,谢谢配合
