在之前的这篇笔记中介绍了SVD的基本原理与在Python中基于Numpy的实现。在这篇博客中则更进一步从原理上介绍了SVD以及它的三大用途：求伪逆、矩阵近似于解方程，并且介绍了SVD在Matlab中的实现及在SLAM中的一些用途。在这篇笔记中介绍了Eigen中利用SVD进行矩阵分解和获得线性方程组最小二乘解的相关内容。在这篇笔记中再一次提到了SVD，在课程中也同样介绍了SVD的三大用途，并且着重介绍了它在解方程中的作用。
所以SVD在之前已经多次提到过了，本篇博客一方面是对之前零碎博客的一些整理，另一方面是侧重SVD在不同库(Eigen、Matlab、Numpy、OpenCV)下的具体实现和一些对比，并不会介绍SVD原理。
1.SVD in Eigen
在Eigen中SVD有多种解法，如BDC、Jacobian等。可以分别调用.matrixU()、.matrixV()、.singularValues()来获得结果。需要注意的是Eigen中SVD分解返回的是U、奇异值向量(不是矩阵，需要手动转成对角阵)、V(不是V的转置，在恢复矩阵时需要手动转置V再相乘)。示例代码如下：
# include<iostream>
#include <Eigen/Dense>
// 对于Windows下的VS注意在导入Eigen库之前需要先在项目的“属性-C/C++-常规-附加包含目录”里添加Eigen库所在目录
// 对于Linux下的CMake，在CMakeLists.txt文件里find_package(Eigen3 REQUIRED)再包含目录即可
using namespace std;
using namespace Eigen;
int main() {
// 测试矩阵，分别为2×3和3×2
Matrix<float, 2, 3> A1;
A1 << 1, 2, 3, 4, 5, 6;
Matrix<float, 3, 2> A2;
A2 << 1, 2, 3, 4, 5, 6;
// 构造SVD对象，除了BDC还有Jacobian等方法
BDCSVD<Eigen::MatrixXf> svd1(A1, ComputeThinU | ComputeThinV);
BDCSVD<Eigen::MatrixXf> svd2(A2, ComputeThinU | ComputeThinV);
// Eigen得到的是奇异值向量以及V，所以需要构造对角阵并对V转置
cout << svd1.matrixU() * svd1.singularValues().asDiagonal() * svd1.matrixV().transpose() << endl;
cout << svd2.matrixU() * svd2.singularValues().asDiagonal() * svd2.matrixV().transpose() << endl;
return 0;
}
2.SVD in OpenCV
在OpenCV中SVD分解的API是cv::SVD::compute()。与Eigen类似也会返回U、特征值向量，不同的是返回的是V的转置而不是V(相当于已经自动帮你转置好了)，可以拿来直接相乘恢复矩阵。示例代码如下：
#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main() {
Mat A1(2, 3, CV_32F);
A1.at<float>(0, 0) = 1;
A1.at<float>(0, 1) = 2;
A1.at<float>(0, 2) = 3;
A1.at<float>(1, 0) = 4;
A1.at<float>(1, 1) = 5;
A1.at<float>(1, 2) = 6;
Mat A2(3, 2, CV_32F);
A2.at<float>(0, 0) = 1;
A2.at<float>(0, 1) = 2;
A2.at<float>(1, 0) = 3;
A2.at<float>(1, 1) = 4;
A2.at<float>(2, 0) = 5;
A2.at<float>(2, 1) = 6;
// 调用OpenCV SVD函数进行计算
// OpenCV返回的是特征向量以及转置后的VT，所以将特征向量变成对角阵后直接相乘即可
// 此外需要注意的是对角阵的大小，与原始矩阵行列较小的那个保持一致，变成方阵
Mat u1, sv1, vt1;
SVD::compute(A1, sv1, u1, vt1);
Mat s1 = Mat::eye(2, 2, CV_32F);
s1.at<float>(0, 0) = sv1.at<float>(0);
s1.at<float>(1, 1) = sv1.at<float>(1);
Mat A1_ = u1 * s1 * vt1;
Mat u2, sv2, vt2;
SVD::compute(A2, sv2, u2, vt2);
Mat s2 = Mat::eye(2, 2, CV_32F);
s2.at<float>(0, 0) = sv2.at<float>(0);
s2.at<float>(1, 1) = sv2.at<float>(1);
Mat A2_ = u2 * s2 * vt2;
cout << A1_ << endl << endl;
cout << A2_ << endl << endl;
return 0;
}
3.SVD in Matlab
Matlab中使用SVD应该是最简单的了，函数名称即是svd()，它返回的是U、奇异值矩阵以及V，在恢复矩阵的时候手动转置一下V再相乘即可得到结果。示例代码如下：
A1 = [1,2,3;4,5,6];
A2 = [1,2;3,4;5,6];
[u1,s1,v1]=svd(A1);
[u2,s2,v2]=svd(A2);
A1_ = u1*s1*transpose(v1);
A2_ = u2*s2*transpose(v2);
A1_
A2_
4.SVD in Numpy
Numpy中SVD分解的函数是np.linalg.svd()，返回结果是U、奇异值向量以及转置后的V，所以将奇异值向量变成奇异值矩阵后，就可以直接相乘得到结果。示例代码如下：
# coding=utf-8
import numpy as np
if __name__ == '__main__':
A1 = np.array([[1,2,3],[4,5,6]])
A2 = np.array([[1, 2],[3, 4], [5, 6]])
# 利用Numpy进行SVD分解
# Numpy返回的是特征值向量以及转置后的VT
u1, sv1, vt1 = np.linalg.svd(A1)
s1 = np.zeros([2,3])
s1[0,0] = sv1[0]
s1[1,1] = sv1[1]
A1_ = np.matmul(np.matmul(u1,s1),vt1)
u2, sv2, vt2 = np.linalg.svd(A2)
s2 = np.zeros([3,2])
s2[0,0] = sv2[0]
s2[1,1] = sv2[1]
A2_ = np.matmul(np.matmul(u2,s2),vt2)
print A1_
print A2_
以上所有代码均上传到了Github，点击查看。
5.Comparison and Conclusion
对于一个m×n的A矩阵，在不同库下的SVD分解结果如下所示。diag表示将奇异值向量转成奇异矩阵(对角阵)，trans表示转置。
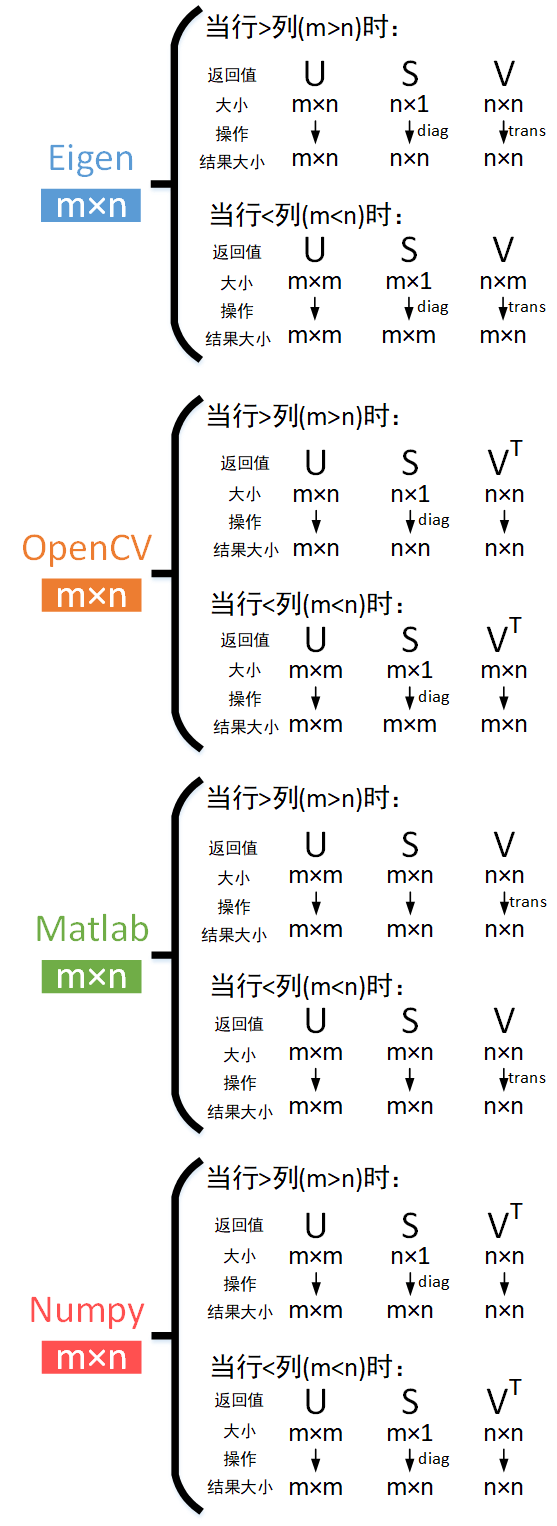由上图可以看出：
- Eigen与OpenCV一样，保持奇异矩阵为方阵，大小与原始矩阵的最小维度相同。不同的是Eigen返回的是V，而OpenCV返回的是VT。所以在恢复矩阵时，一个要先转置再乘，一个直接乘。
- Matlab与Numpy相同，通过保持奇异矩阵与原始矩阵大小相同，使得U、V都为方阵且不随原始矩阵大小关系的变化而变化。不同的是Matlab返回的是奇异值矩阵、V，而Numpy返回的是奇异值向量、VT。所以在恢复矩阵时，一个要先转置再乘，一个构造奇异矩阵后直接乘。
其实从上面也可以看出，SVD分解有两类不同形式。一类是使中间的奇异矩阵与原始矩阵大小相同(如Matlab和Numpy采用的方法)，这样的好处是U、V分别为方阵，大小分别为原始矩阵的高和宽，且不会随原始矩阵行列关系变化而变化；另一类是保持奇异矩阵为方阵(如Eigen和OpenCV采用的方法)，U、V随原始矩阵行列关系变化而变化，又可以细分为行>列和行<列两种情况(行列相等的情况两种都适用)。
因此，对于一个形状为m×n的A矩阵，对其进行SVD分解，可以有以下情况：
- 当奇异矩阵与原矩阵相同大小时：
- 当奇异矩阵为方阵且原始矩阵行>列时：
- 当奇异矩阵为方阵且原始矩阵行<列时：
本文作者原创,未经许可不得转载,谢谢配合
