1.Visual Odometry
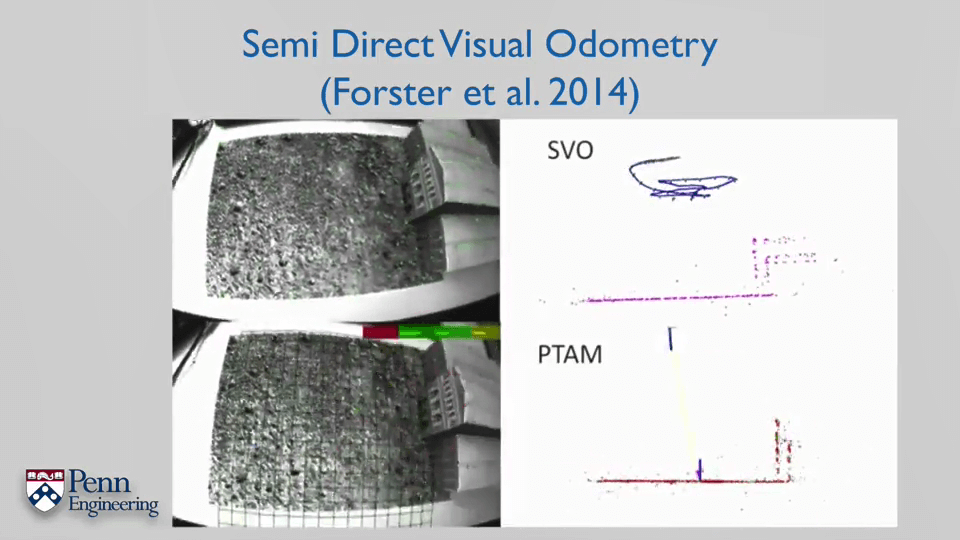
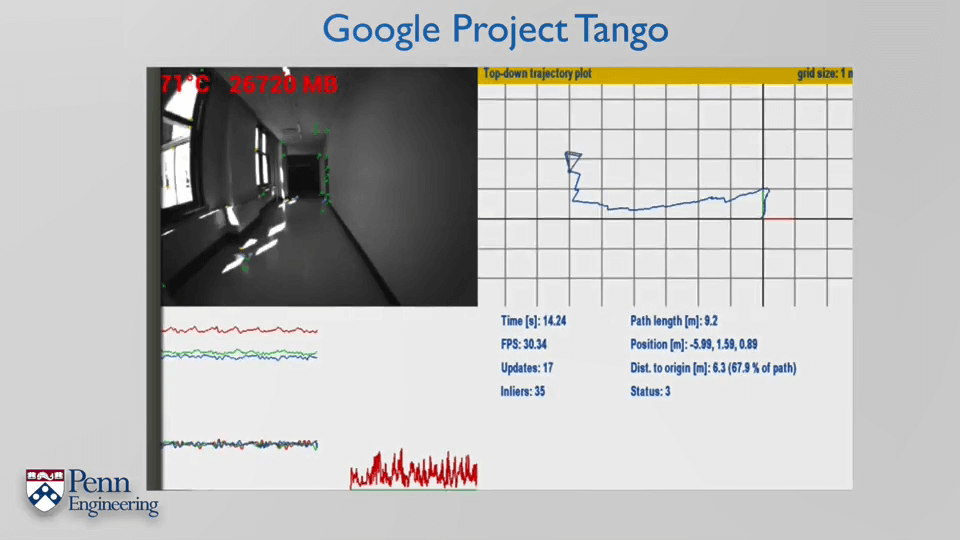
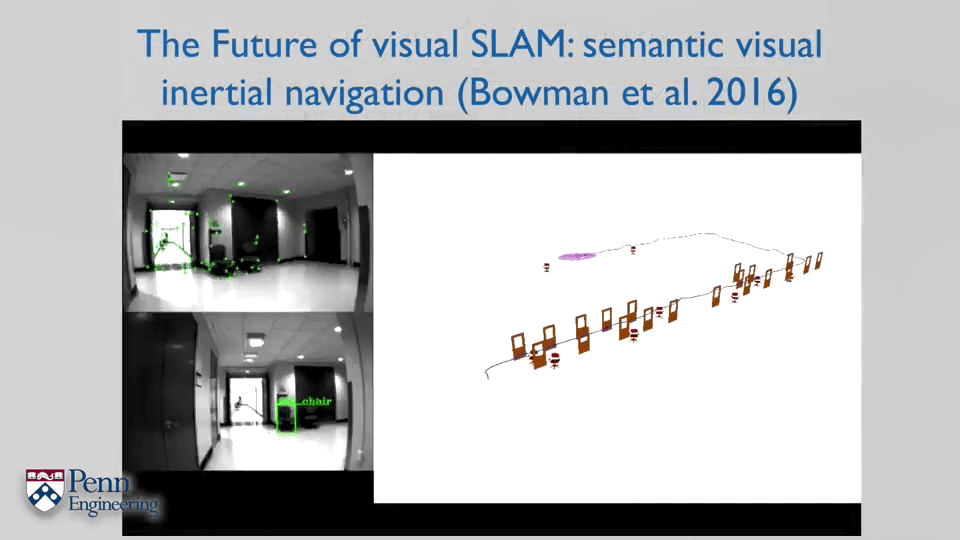
2.Bundle Adjustment Part1
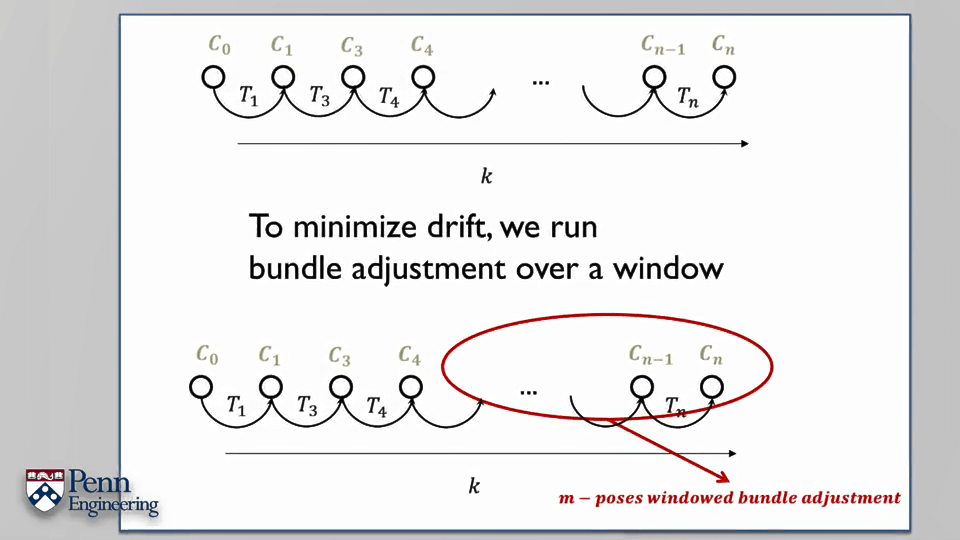
一切都从两个基本问题出发：我在哪？某个点在3D坐标系的位置是什么？
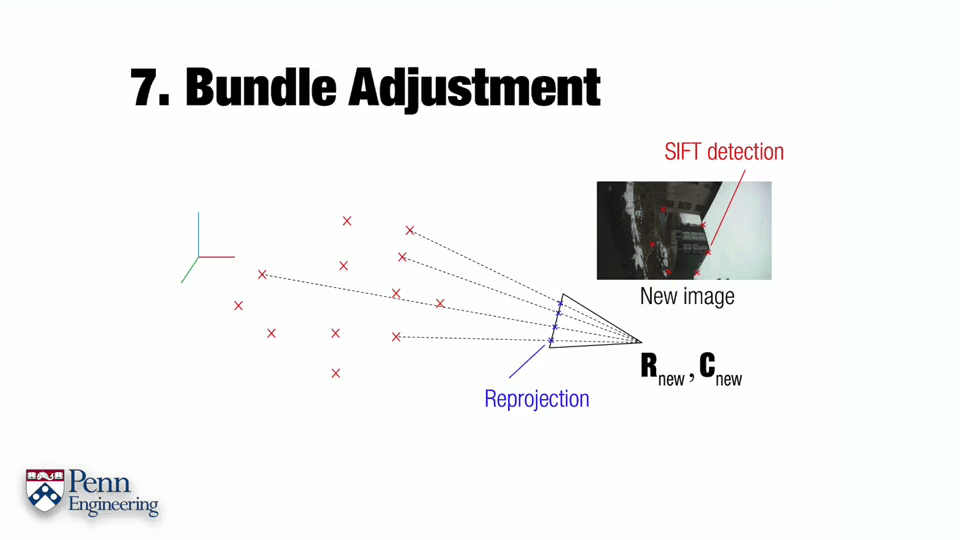
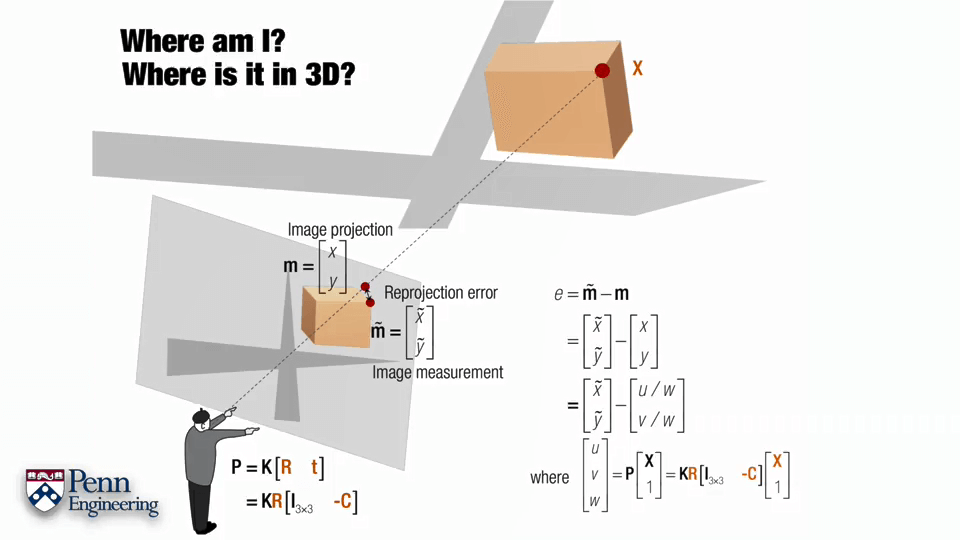由于估计的投影矩阵P有误差，进而导致投影回到像平面的点m和我们观测的m~点坐标有差异，这个差异e可以理解为重投影误差，也就是我们需要尽可能减小的。
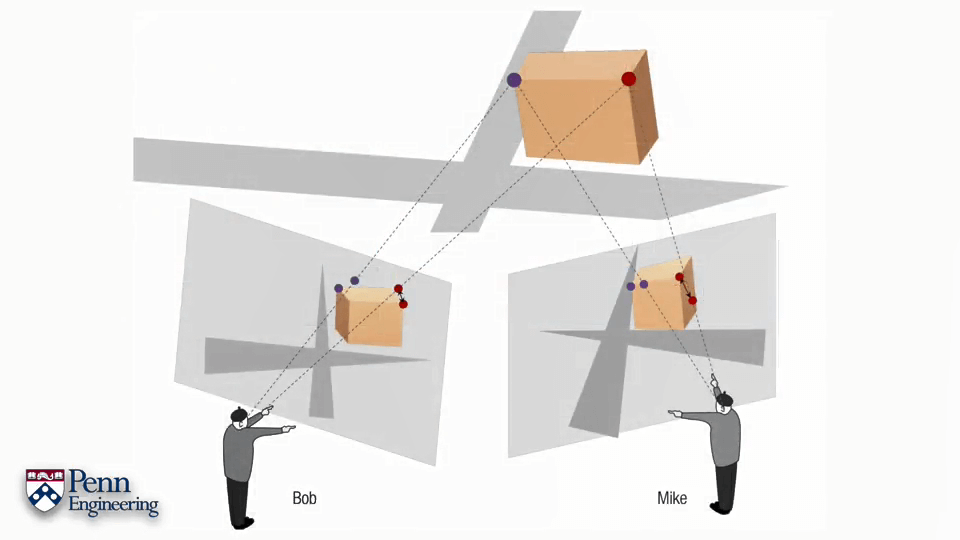
这里C是相机光心在世界坐标系中的坐标，X为该点在世界坐标系中的坐标，R为相机姿态。这三个橙色的字母就是我们需要调整优化的变量。
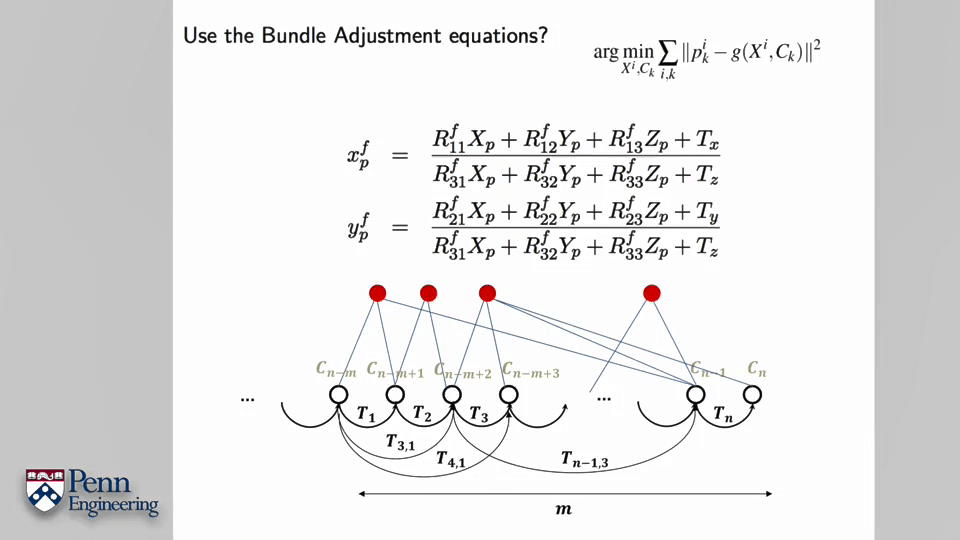
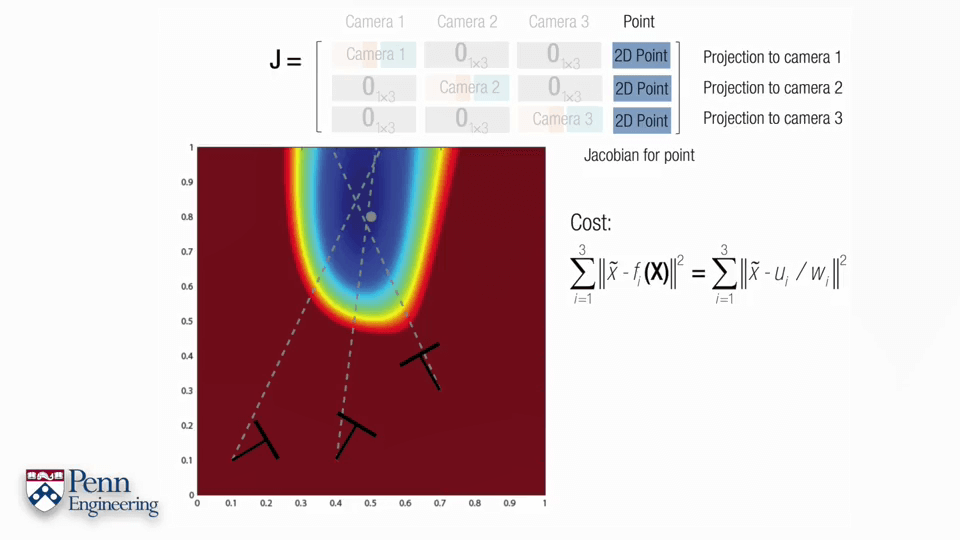
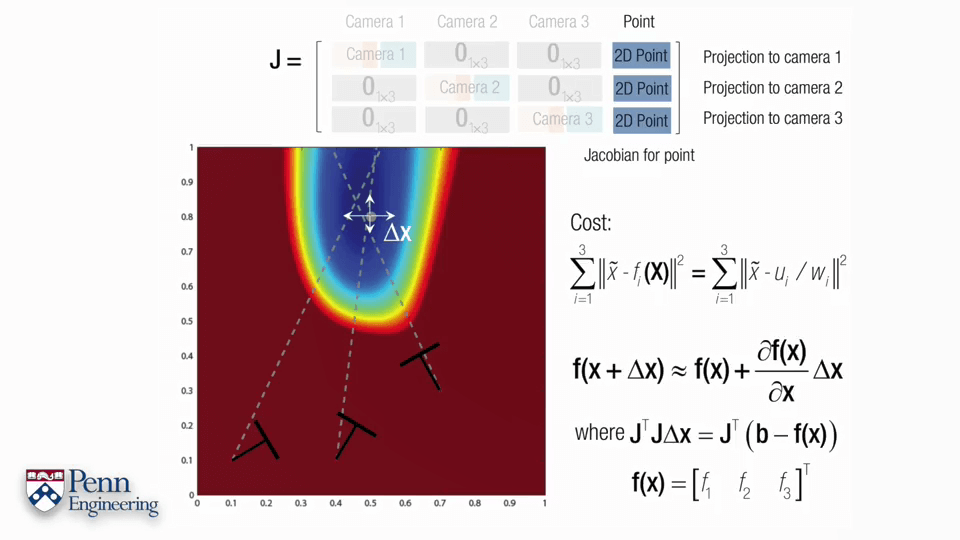
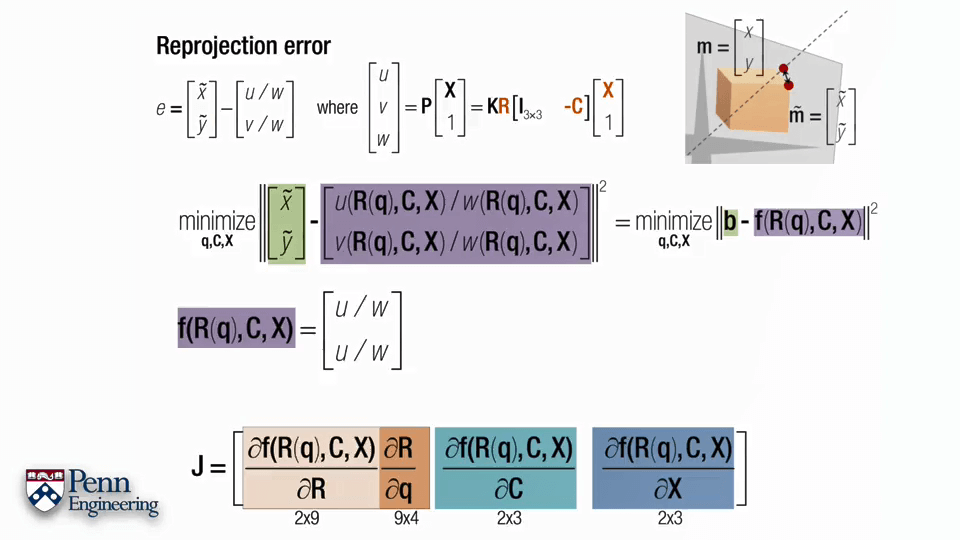
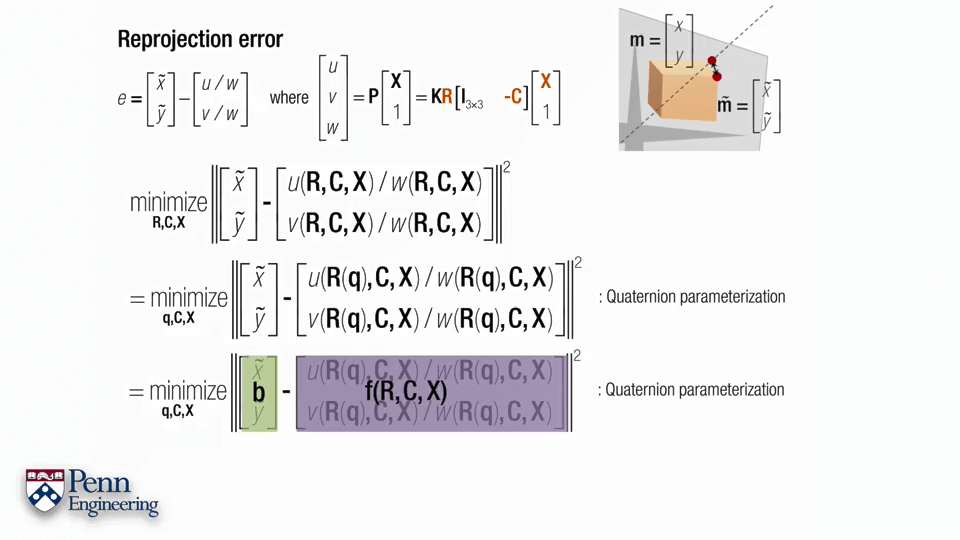对于某个点，重投影误差可以如上图所示。x~、y~是我们在影像上的观测坐标，u、v、w则是根据估计的相机位姿算出来的该点坐标。这个式子中最复杂的也就是后半部分，也正是因为它导致了整个式子的非线性。更具体来说u、v、w的计算是非线性的，而u/w、v/w又是非线性的。为了后续方便，不妨将u、v、w写成关于R、C、X的函数形式，如第二行。进一步，旋转R可以参数化表达为四元数，可以写成第三行。以非线性最小二乘的形式可以看成b-f(R,C,X)的形式，如第四行。
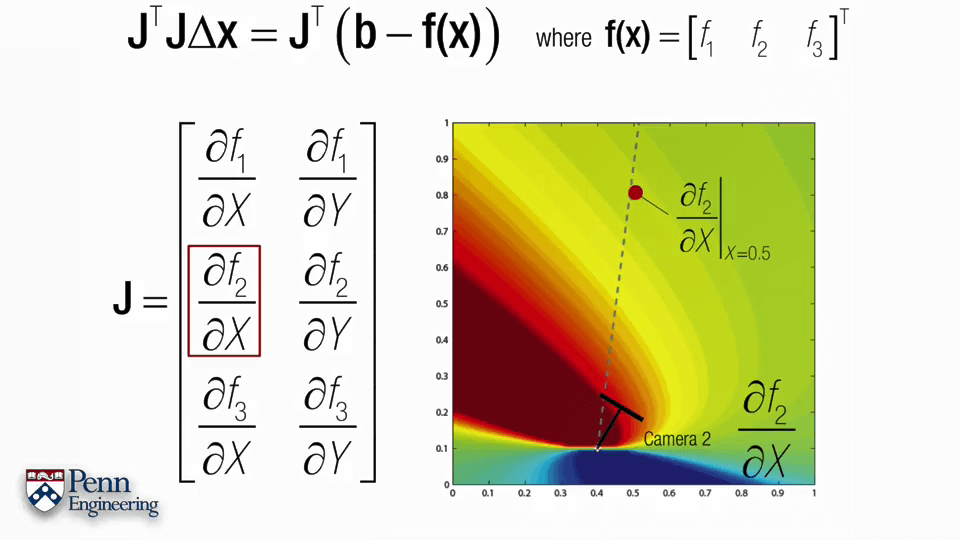
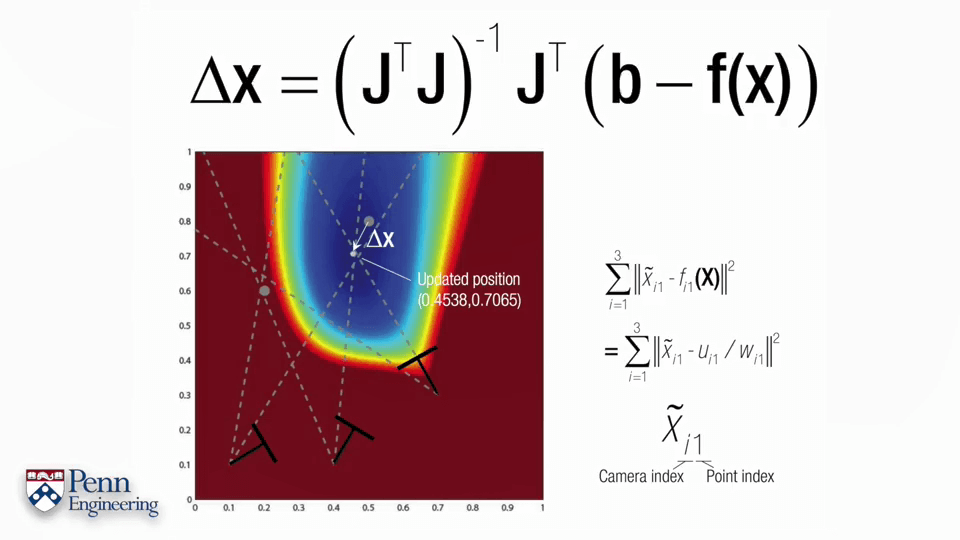
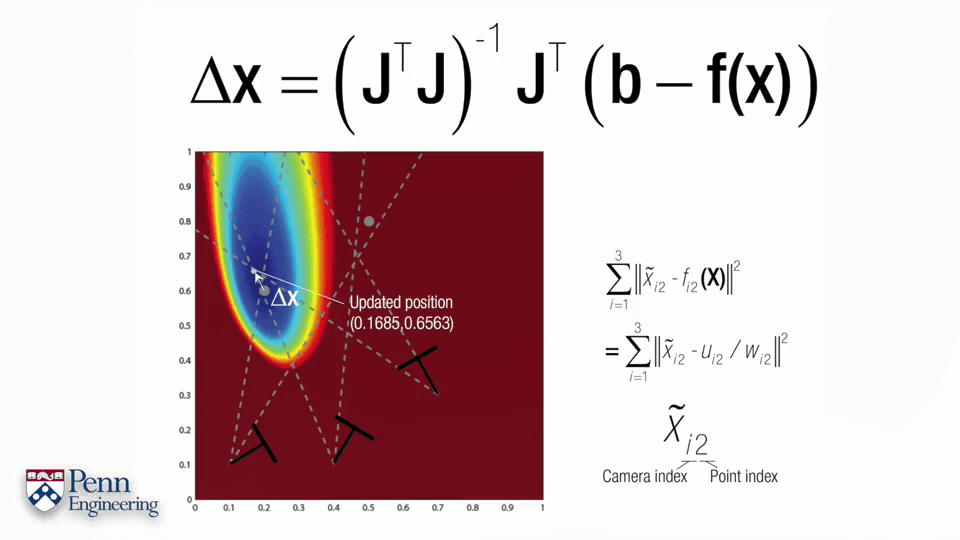
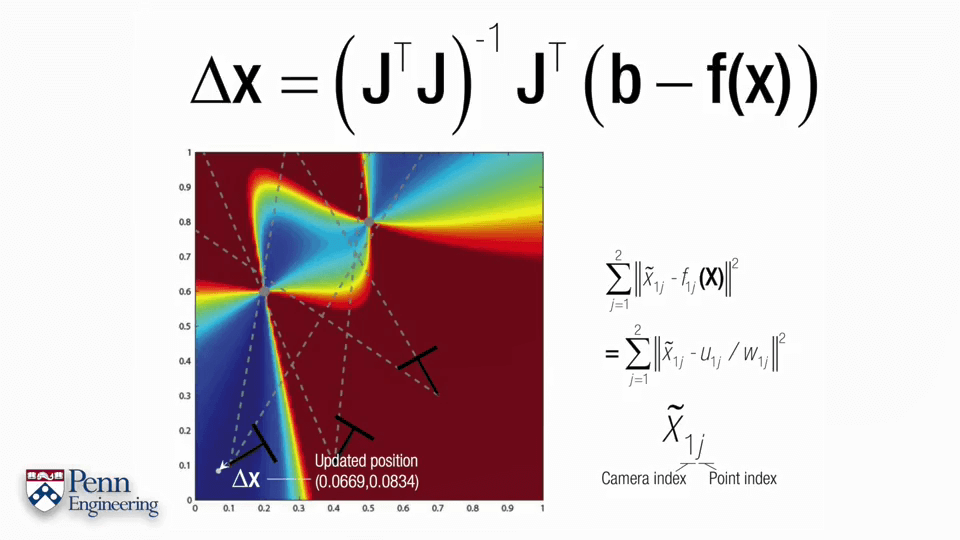
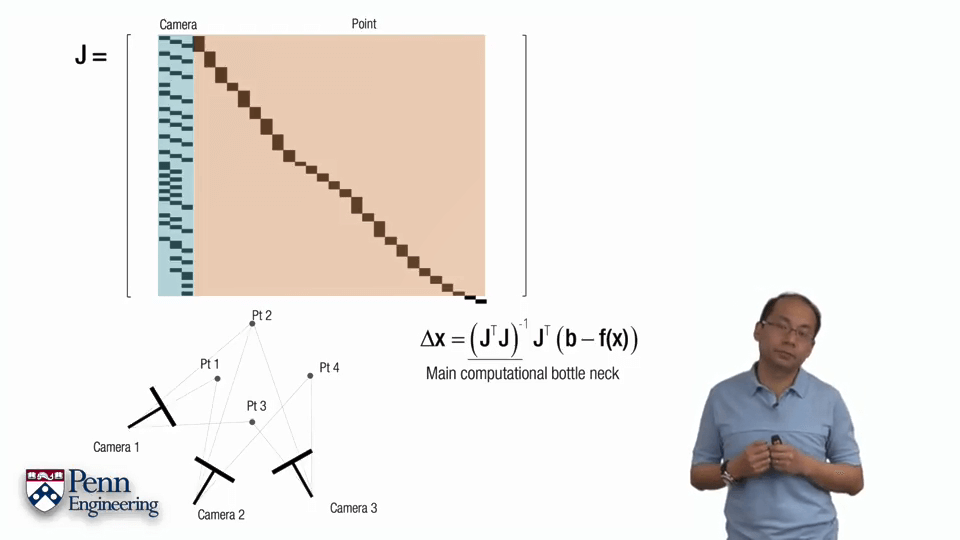
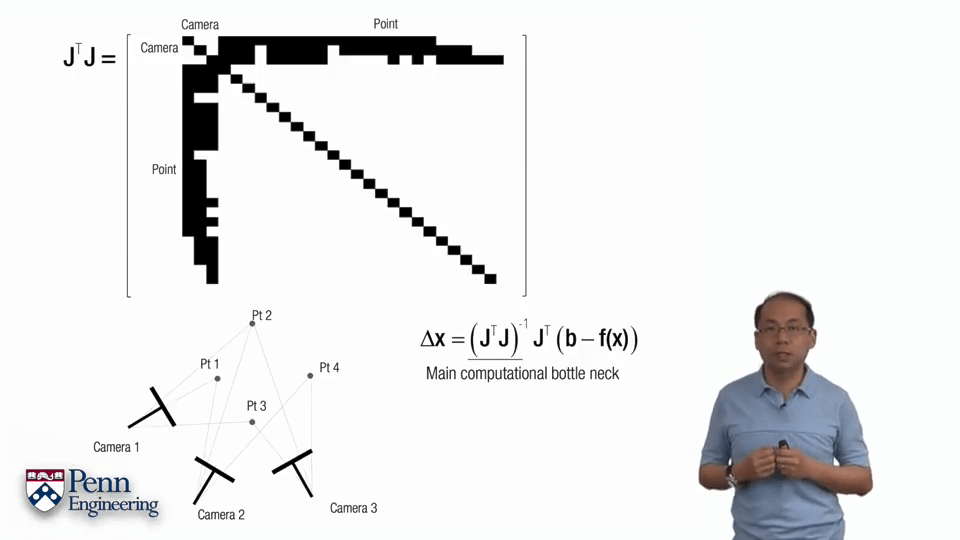
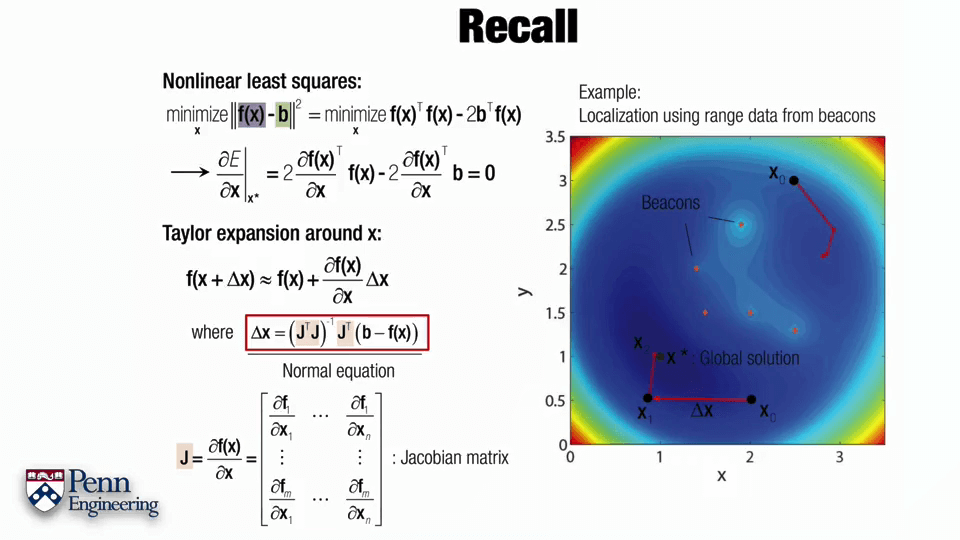一个标准的非线性最小二乘问题如上图所示，主要分为两步。首先计算误差函数的导数，并让其为0。第二步是对函数进行泰勒展开。这里Δx的式子叫做normal equation，通过求解这个式子就可以获得Δx进而可以不断迭代，是非常重要的式子。可以看到normal equation包含两个内容，一个是雅可比矩阵J，一个是负的error function。某种程度上来说，求解normal equation就是求解雅可比矩阵J，求解出了雅可比矩阵J就可以得到normal equation，得到normal equation就可以得到Δx进而不断迭代。这里的J是雅可比矩阵，是一个m行n列的矩阵。对于每一个自变量x都有一列与其对应，对于每一个约束，都有一列与其对应。对于第i列，其元素是各个f对xi的偏导，对于第j行，每个元素是fj对于每个自变量的偏导。更直白地说，雅可比矩阵的行数代表观测个数，列数表示每次观测的变量的个数。
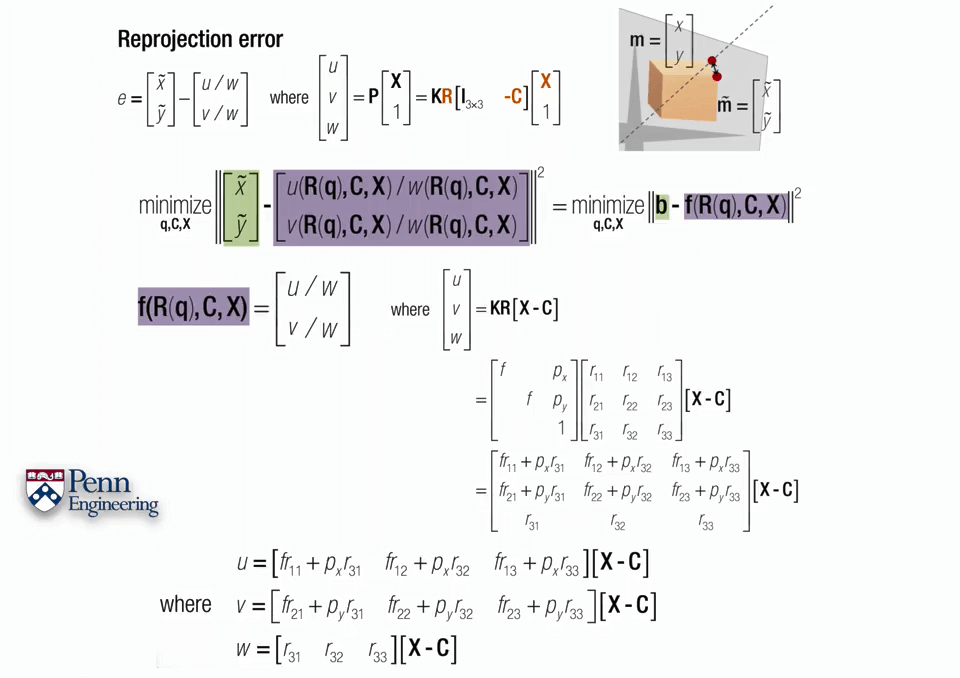回到我们的重投影误差问题。正如刚刚说的雅可比矩阵的求法，是要对f(x)求偏导的，因此需要写出f(x)明确的形式。在这里f(x)是由u、v、w组成的，进一步将其写成关于自变量R、C、X的形式，便于后续求偏导。
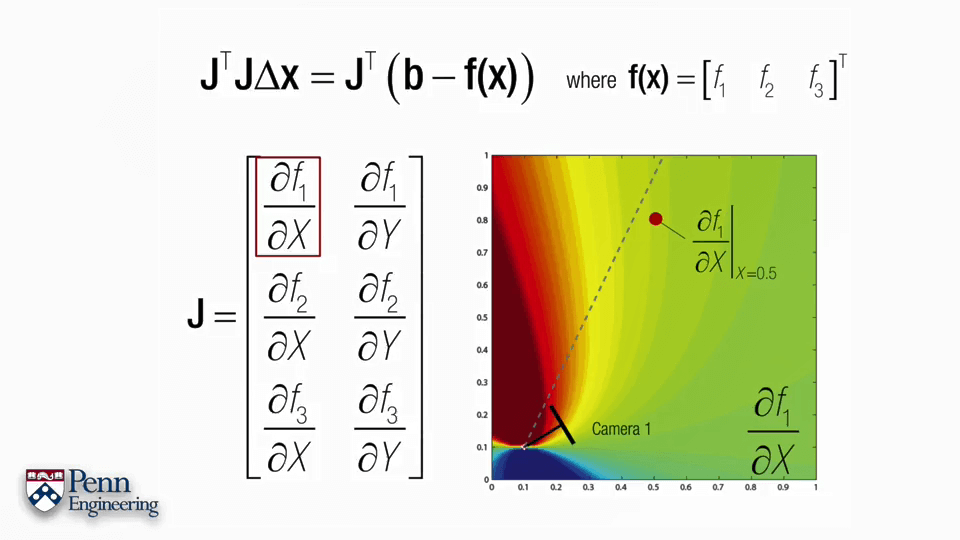
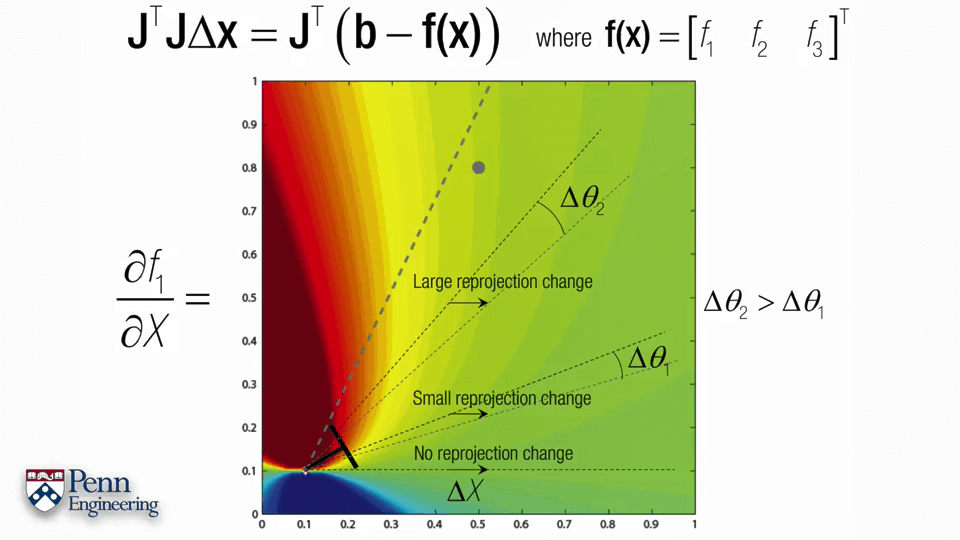
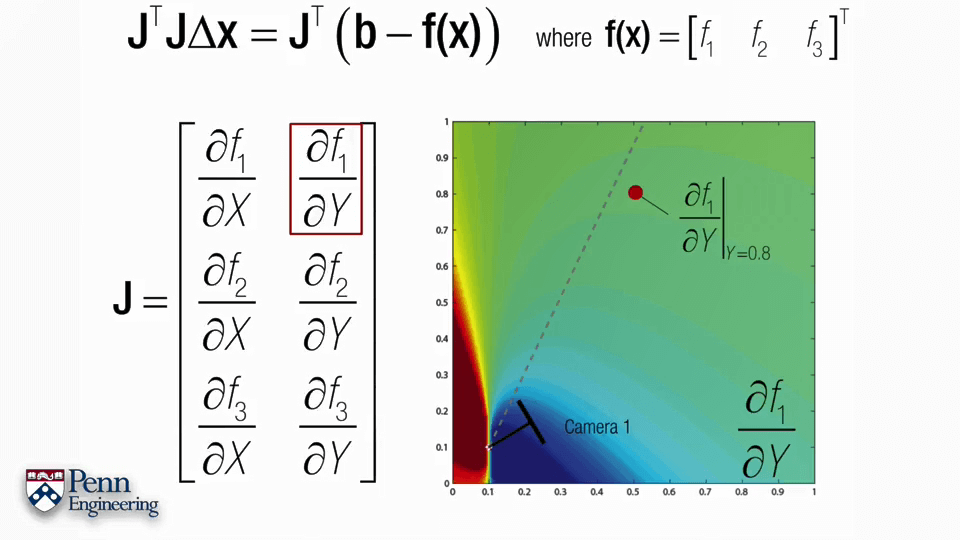
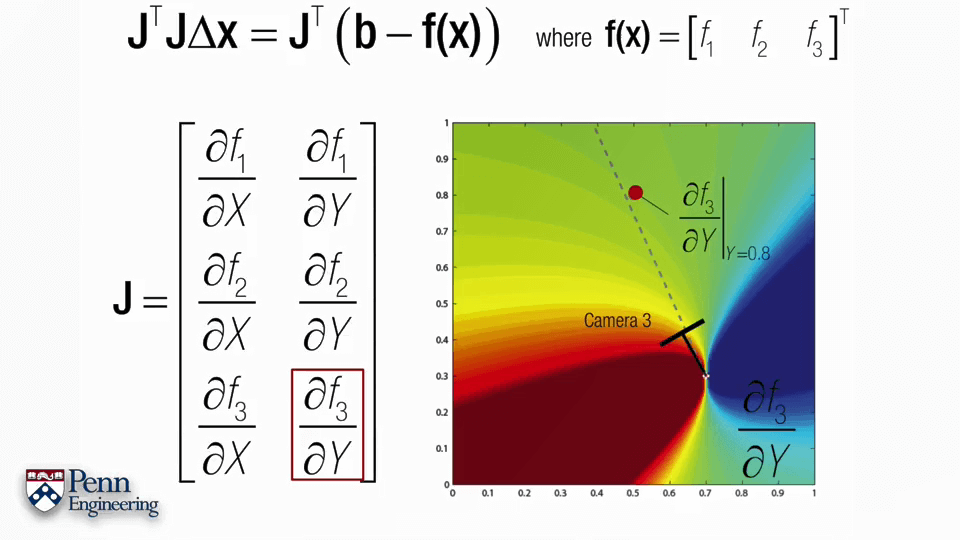
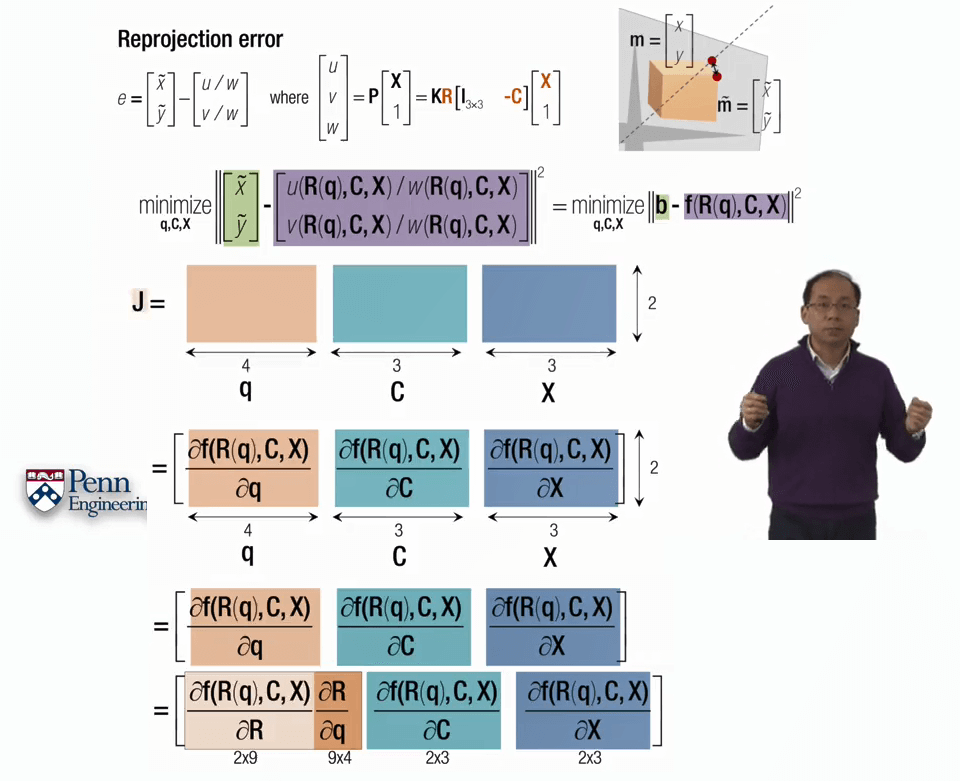有了f(x)，下一步的关键问题就是雅可比矩阵J该怎么求。正如上面提到的雅可比矩阵的特性，雅可比矩阵的每一列与我们正在搜寻的未知变量有关，每一列表示对一个变量的偏导，列数等于变量个数，而f(x)又是关于R、C、X的变量，所以不妨将雅可比矩阵J拆分成R、C、X三部分。同时别忘了我们用四元数表示R，这样根据求导的链式法则就可以获得J的三部分q、C、X，q是四元数，包含4个变量，C和X都是三维坐标，包含3个变量，因此J总共包含4+3+3=10列。而我们在影像上的观测是x~、y~，有两个变量，因此J的行数为2。
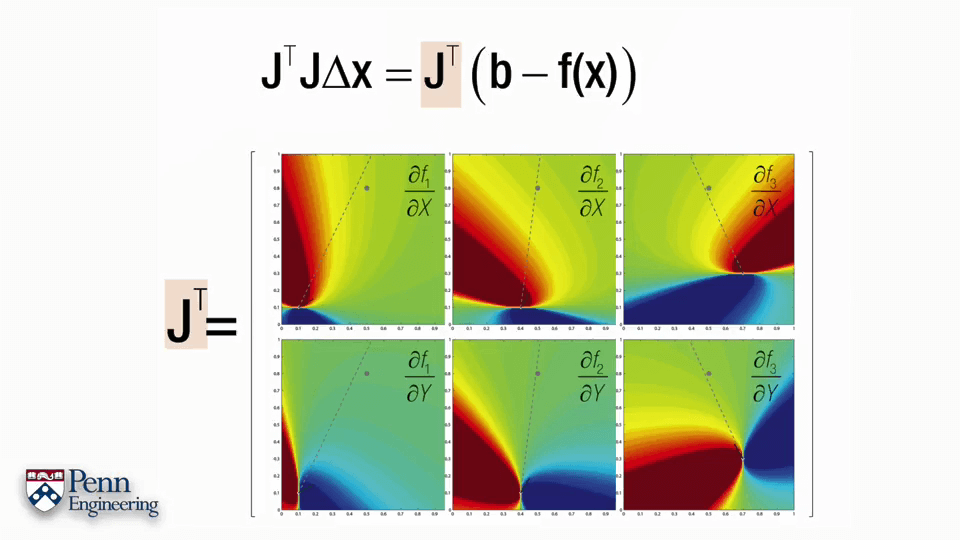
因此我们可以依次获得各部分的矩阵，最后组成一个完整的雅可比矩阵J。对于一个点，可以获得一个2行10列的雅可比矩阵。而对于n个点，可以以此类推获得2n行10列的大的矩阵。
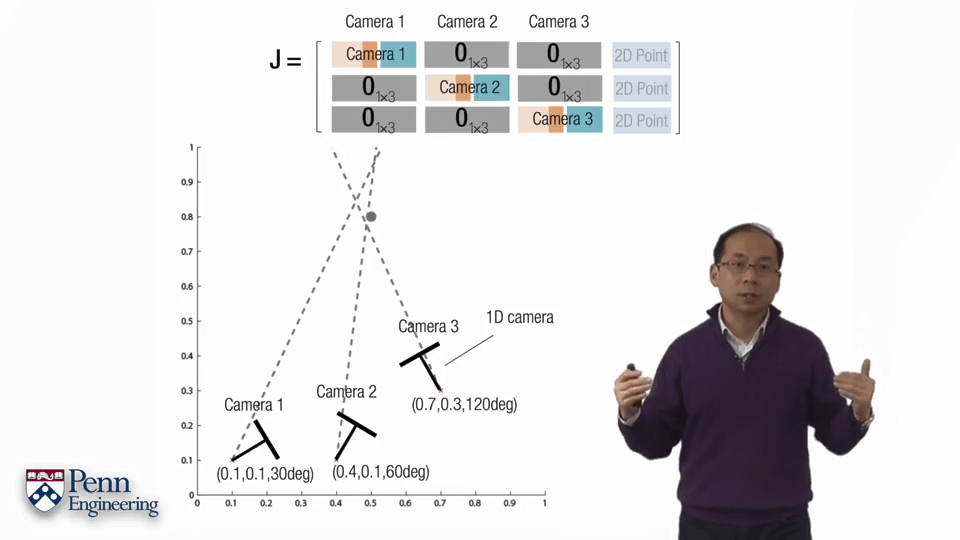
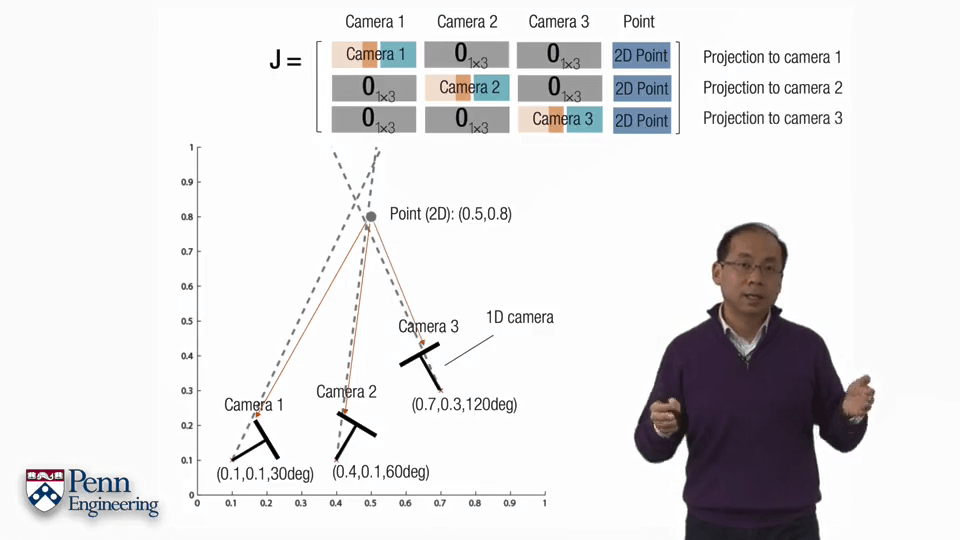
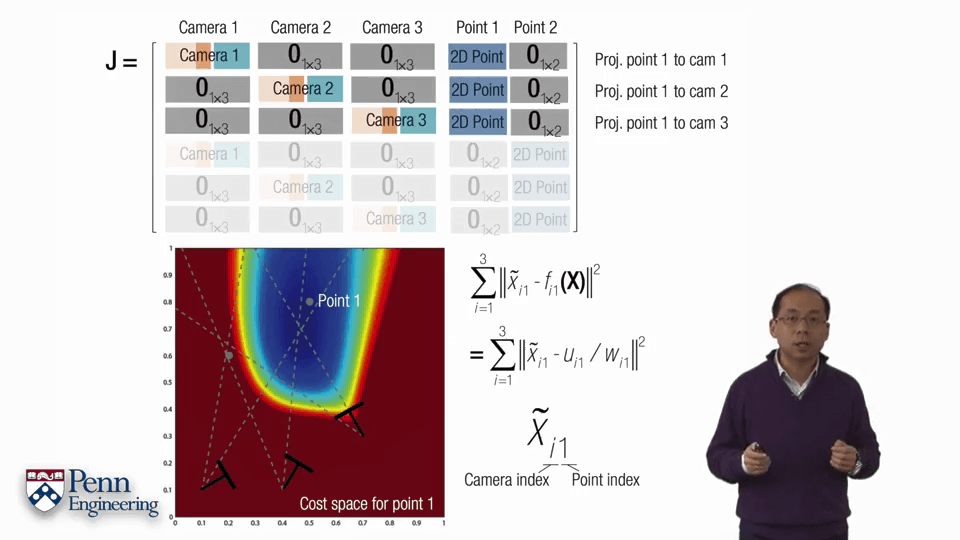
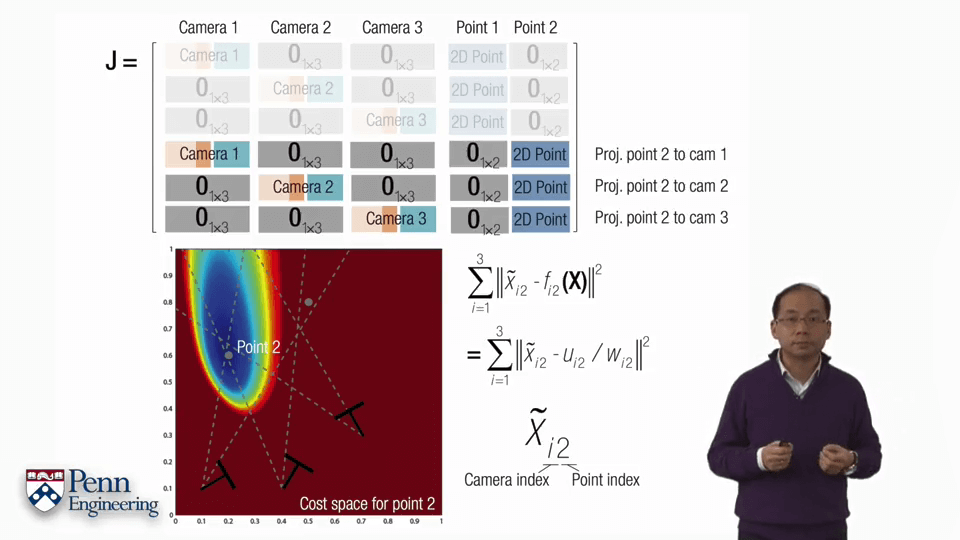
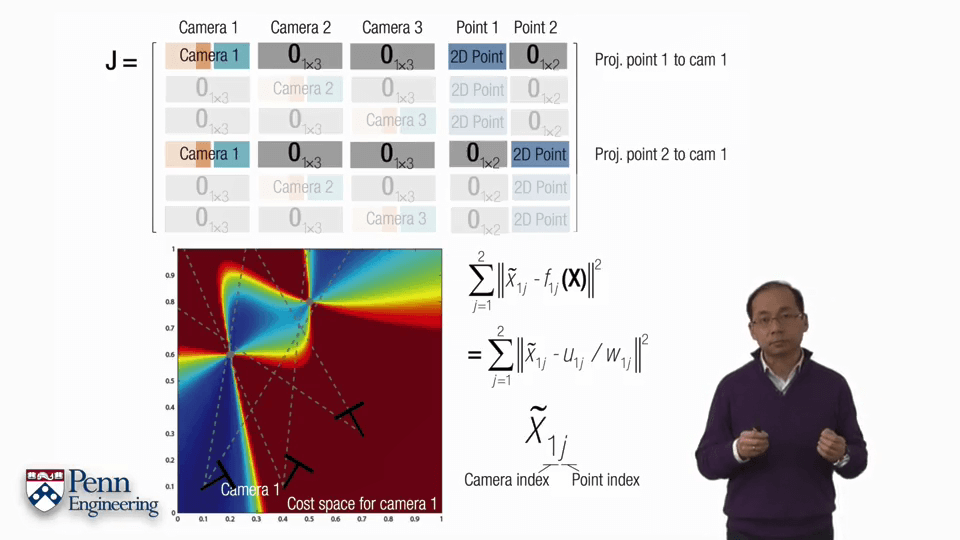
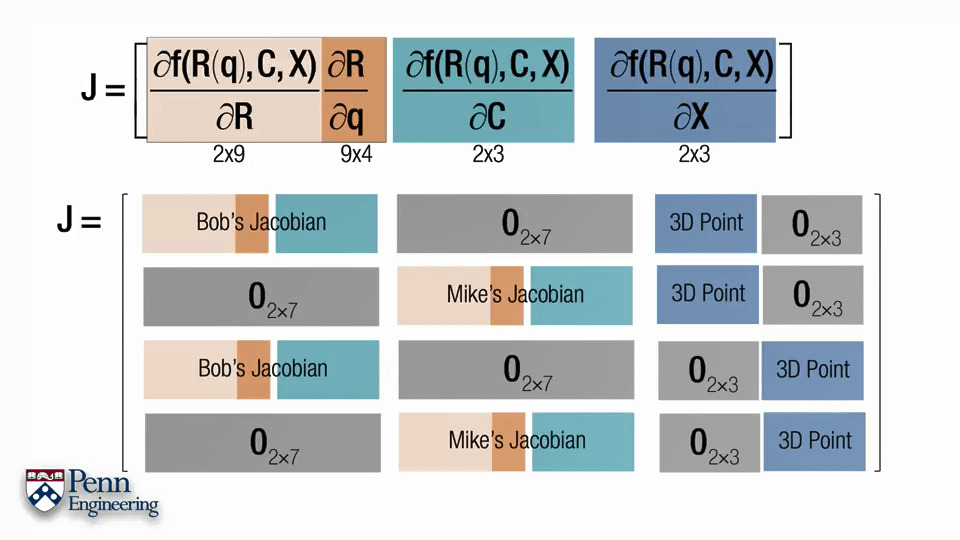
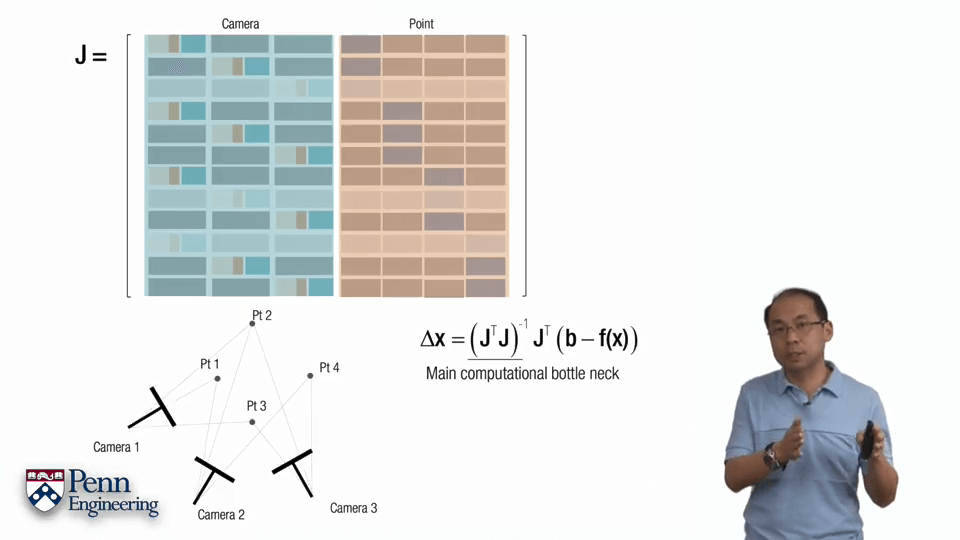
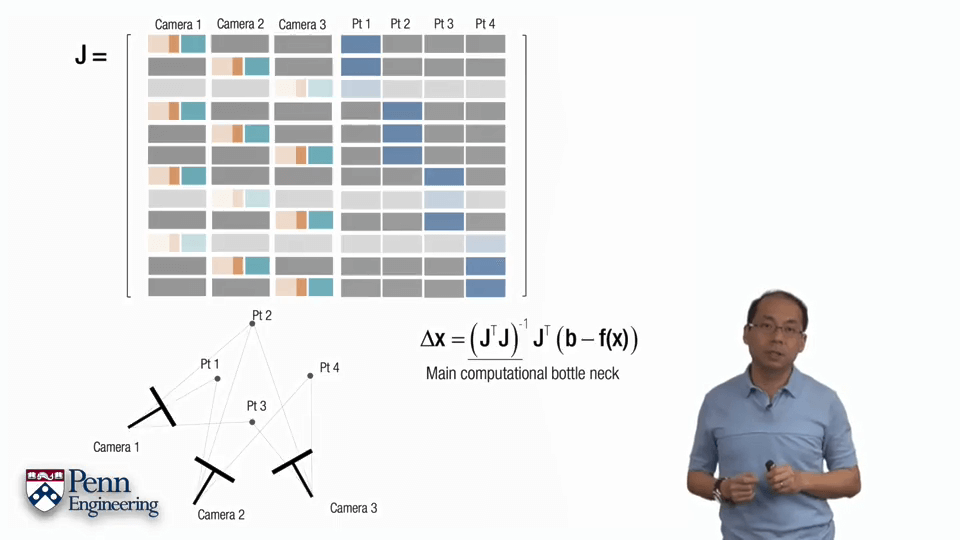
但上面所说针对的是一个影像中的一个点的情况，对于多帧的情况就会有所不同。可以按照上图中的形式拼接多个不同帧的雅可比矩阵。因为各帧之间的观测并不会互相干扰，因此空白部分全部为0。对于某个在两帧中都观测到的点，每一帧中的雅可比矩阵是2行17列，拼起来就是4行17列的大的矩阵。
3.Bundle Adjustment Part2
下面以一个例子介绍一下BA的过程。
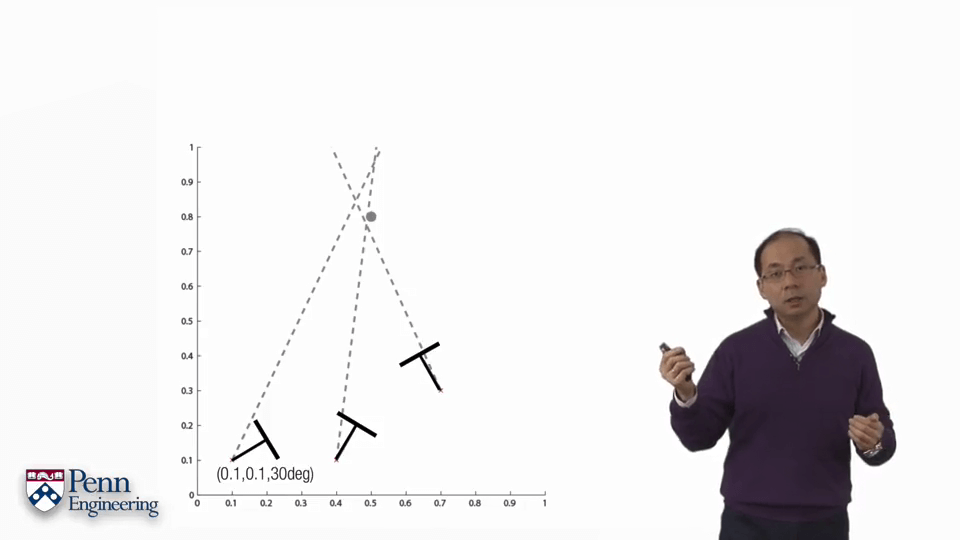
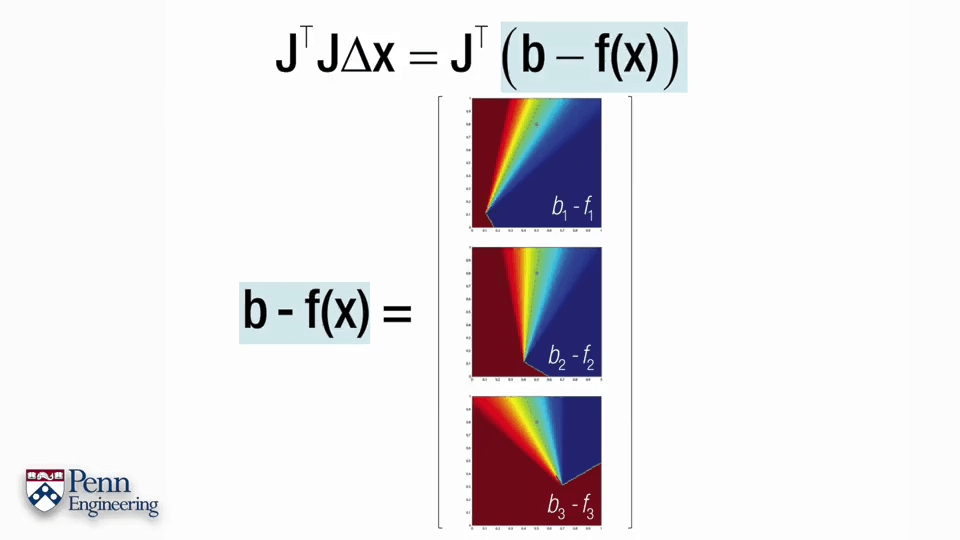
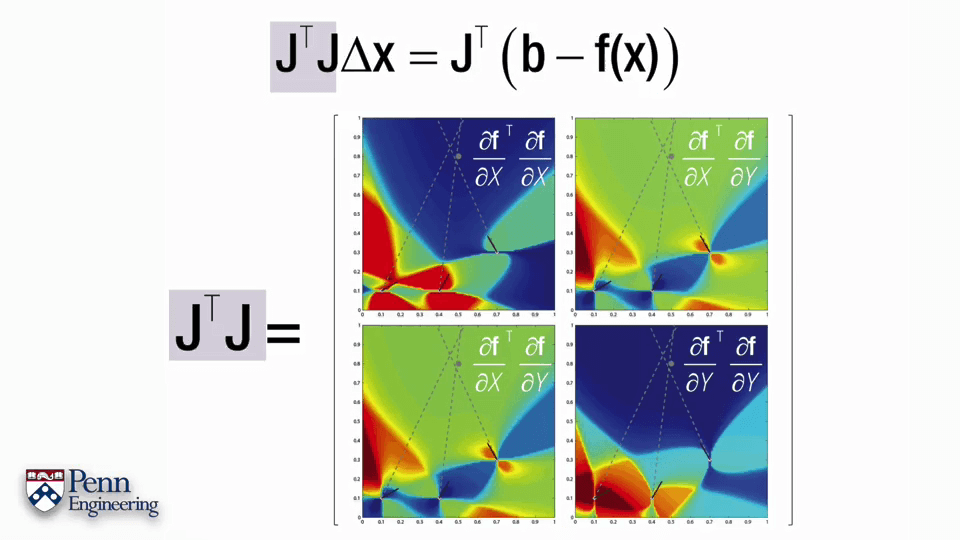
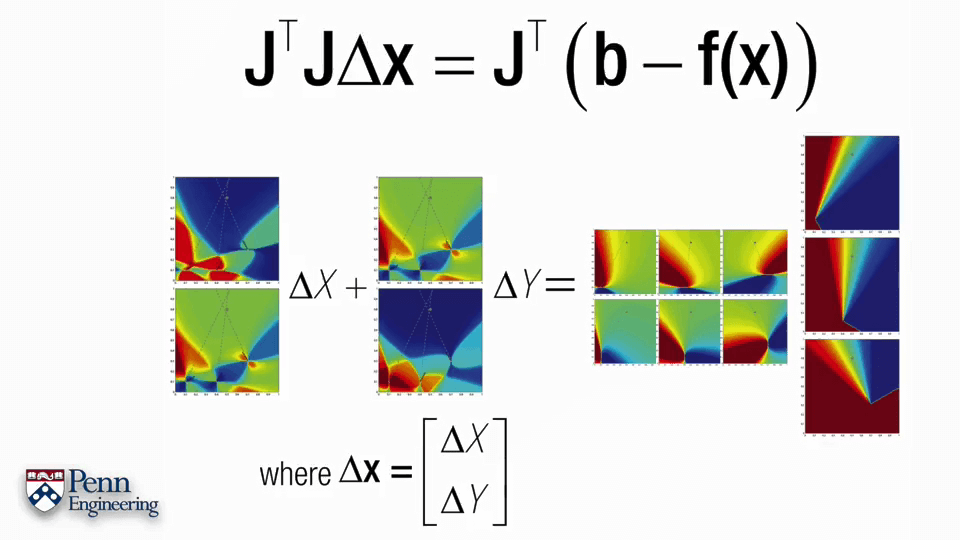
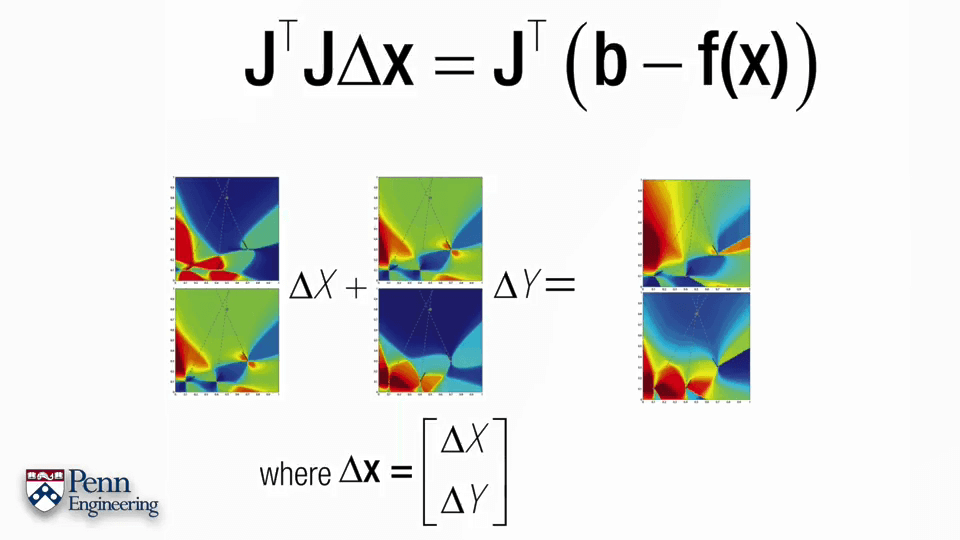
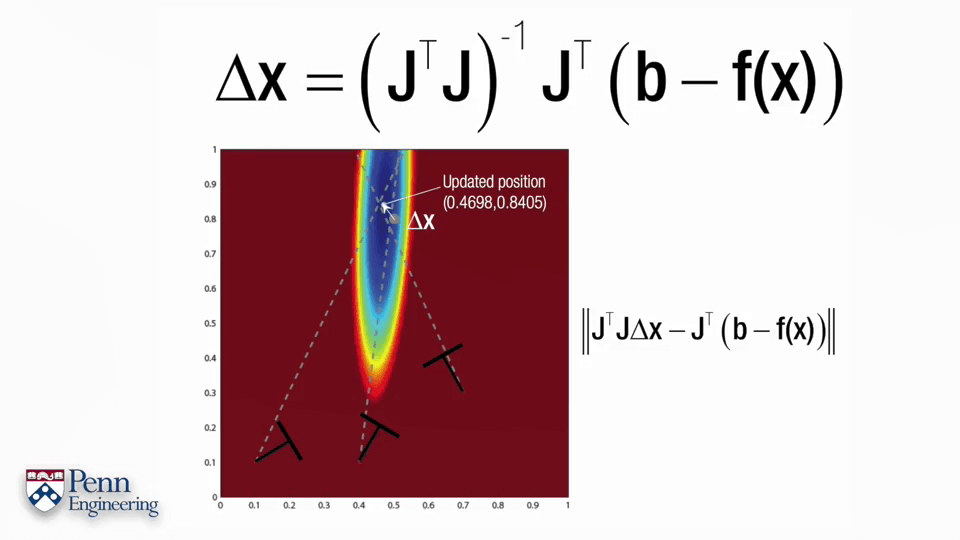
4.Bundle Adjustment Part3
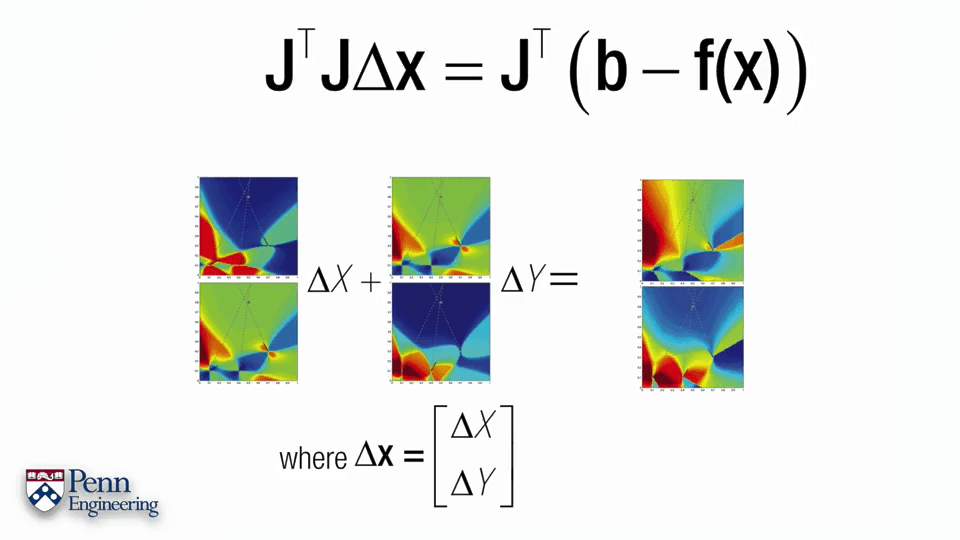
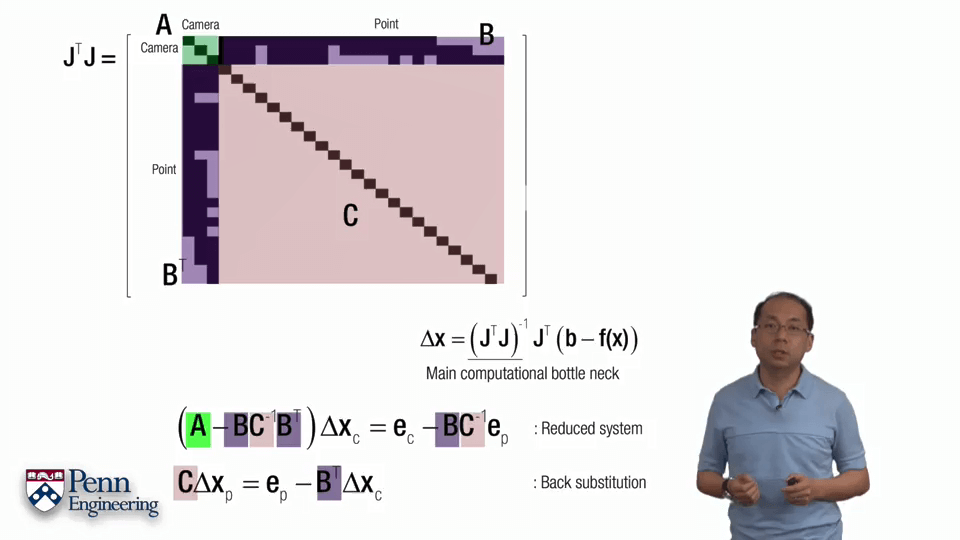
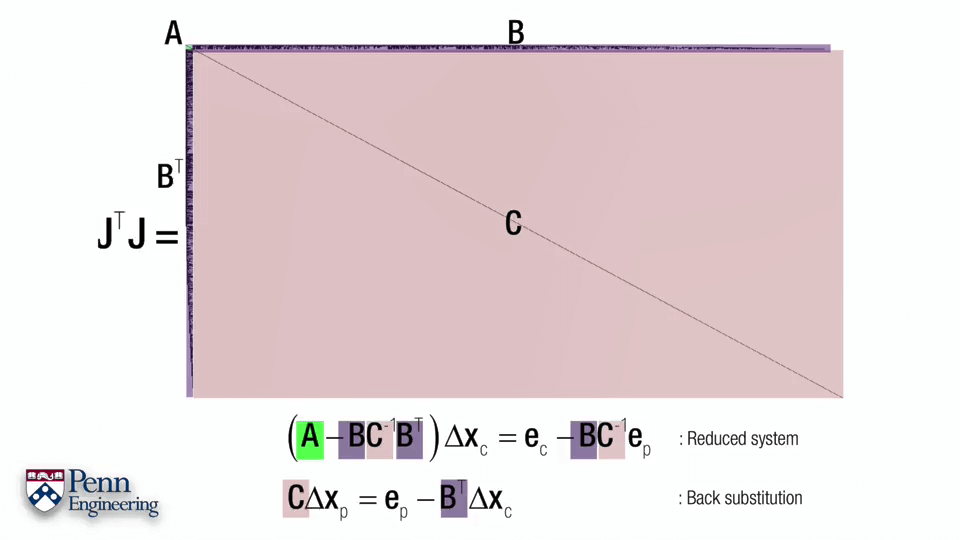
本文作者原创,未经许可不得转载,谢谢配合
