- 1.Optical Flow:2D Point Correspondences
- 2.3D Velocities from Optical Flow
- 3.3D Motion and Structure from Multiple Views
1.Optical Flow:2D Point Correspondences
前面有提到过,通过在不同视角的影像上找到对应的特征点,基于此可以三角化恢复一些三维信息。那么如何获得这些对应的点呢?光流法就是其中的一个办法。例如如下图所示,相邻帧之间的运动非常小。这其实也是光流应用的前提之一了。
 对上面的情况进行抽象。如下有两个影像I和J,它们之间存在一个幅度不大的平移d,我们可以将其写成公式表示如下。这里的I(x)和J(x)可以看作是以像素位置x为自变量与像素灰度为因变量的映射函数。
对上面的情况进行抽象。如下有两个影像I和J,它们之间存在一个幅度不大的平移d,我们可以将其写成公式表示如下。这里的I(x)和J(x)可以看作是以像素位置x为自变量与像素灰度为因变量的映射函数。
 假如我们能够准确找到这个平移d,那么就可以找到两个影像的对应关系了。那么不妨从优化的角度考虑这个问题,如下图所示。
假如我们能够准确找到这个平移d,那么就可以找到两个影像的对应关系了。那么不妨从优化的角度考虑这个问题,如下图所示。
 我们的优化变量就是平移d,通过不断调整这个二维的平移d,使得J和I相减的差值最小。这个问题显然是一个非线性最小二乘问题。那么对于这个问题,可以按照以下三步进行求解。第一步就是对自变量d求导并使导数为0;第二步是将非线性的目标函数用泰勒级数展开,变成线性形式;第三步是迭代求解。下面详细讲解。这部分的内容需要有Week 4 Part 1里非线性最小二乘的基础,如果不太理解可以回去看相关笔记。
我们的优化变量就是平移d,通过不断调整这个二维的平移d,使得J和I相减的差值最小。这个问题显然是一个非线性最小二乘问题。那么对于这个问题,可以按照以下三步进行求解。第一步就是对自变量d求导并使导数为0;第二步是将非线性的目标函数用泰勒级数展开,变成线性形式;第三步是迭代求解。下面详细讲解。这部分的内容需要有Week 4 Part 1里非线性最小二乘的基础,如果不太理解可以回去看相关笔记。
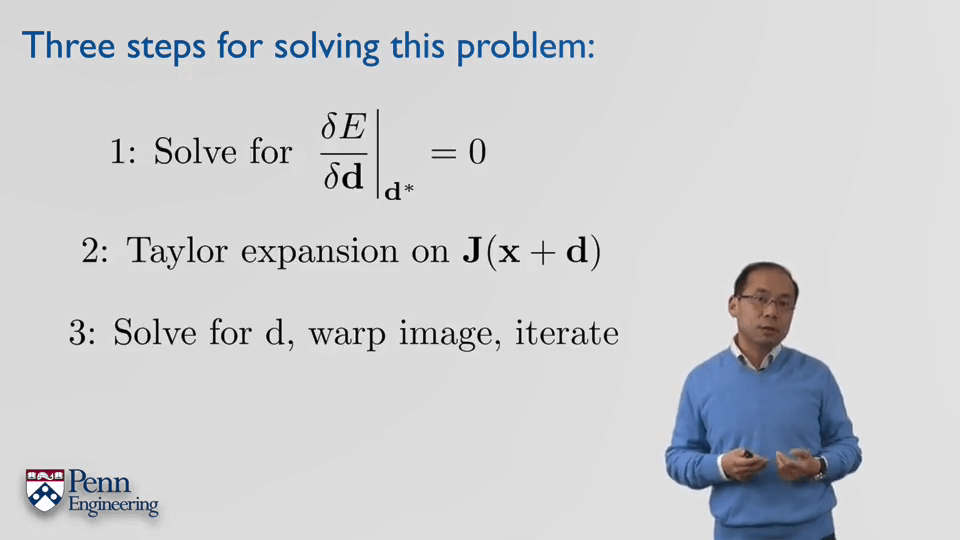
第一步就是求解目标函数关于自变量的导数,对应f(x)-b的形式,将J(x+d)认为是f(x),I(x)是b,那么很容易就可以得到误差E的表达为f(x)Tf(x)-2bTf(x),对这个误差函数求导数并使其导数为0,即可以得到下面的式子。这个式子在Week 4 Part 1里也有提到,可以当作公式记下来。δf(x)/δx其实就是雅可比矩阵,每一列表示对某一个变量的偏导,每一行表示某次观测。

第二步是对J(x+d)泰勒展开(一阶),然后将其带回到误差函数的导数中去,如下图所示。这里蓝色部分就是J的雅可比矩阵。
 稍作整理,即可得到如下式子。
稍作整理,即可得到如下式子。
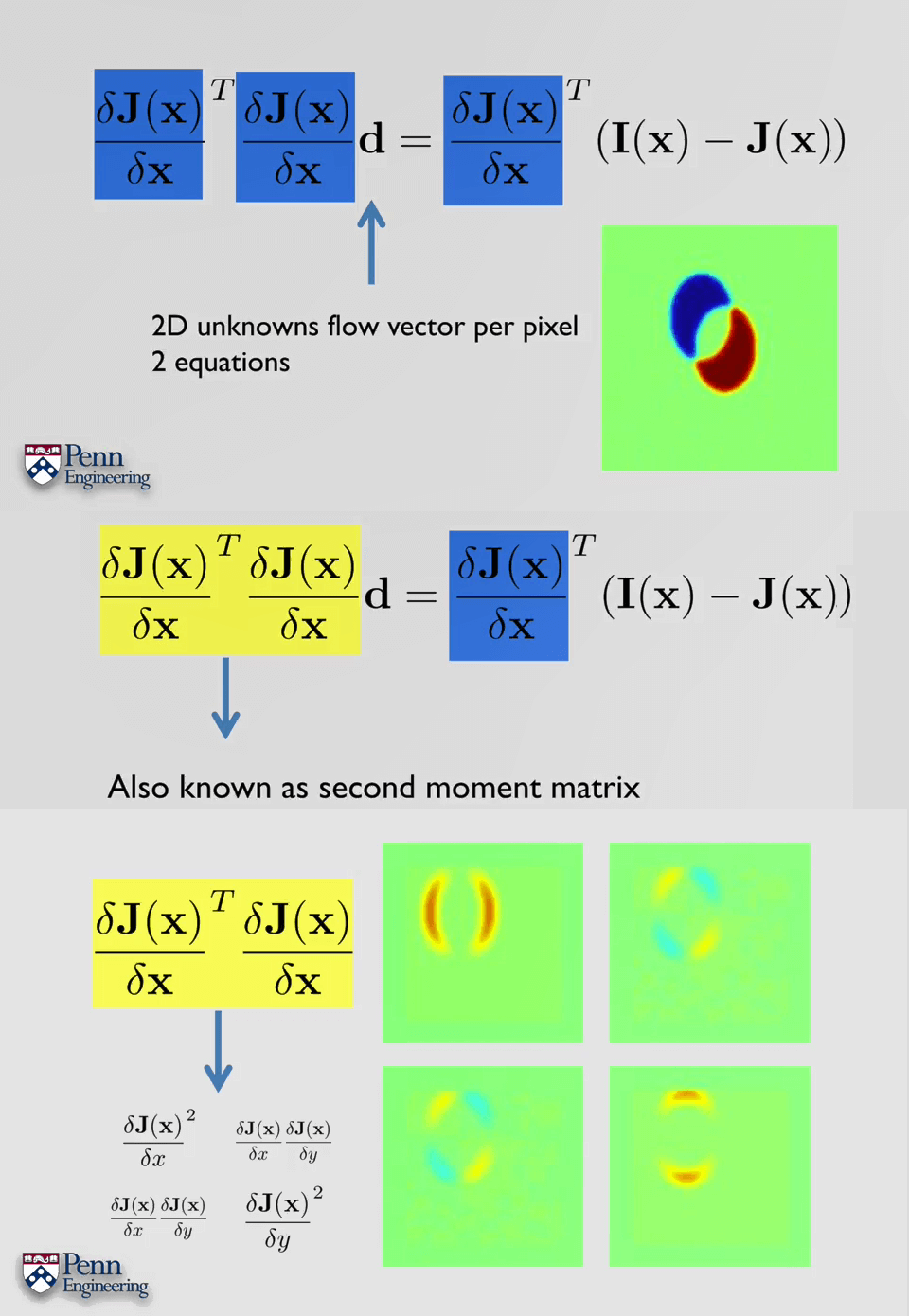
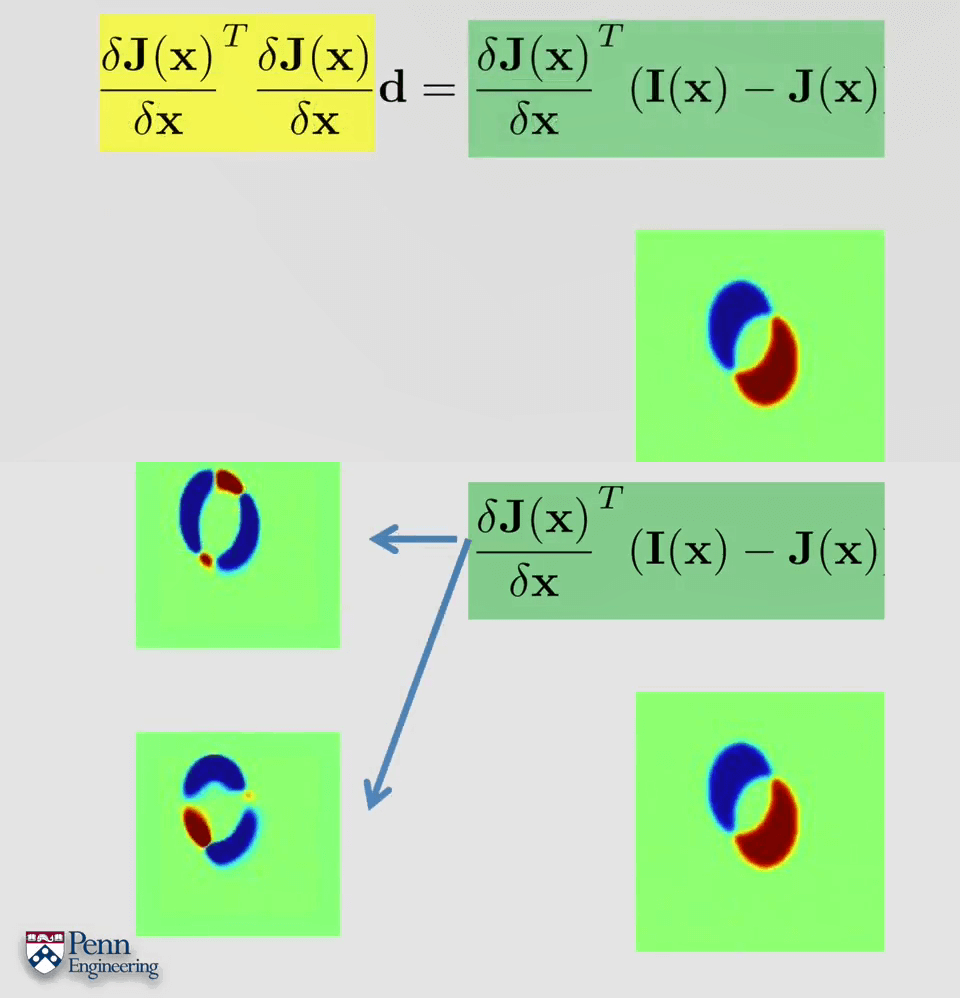
 上面是对于每个像素的误差,最终还需要将这些误差求和,得到总的误差。
上面是对于每个像素的误差,最终还需要将这些误差求和,得到总的误差。
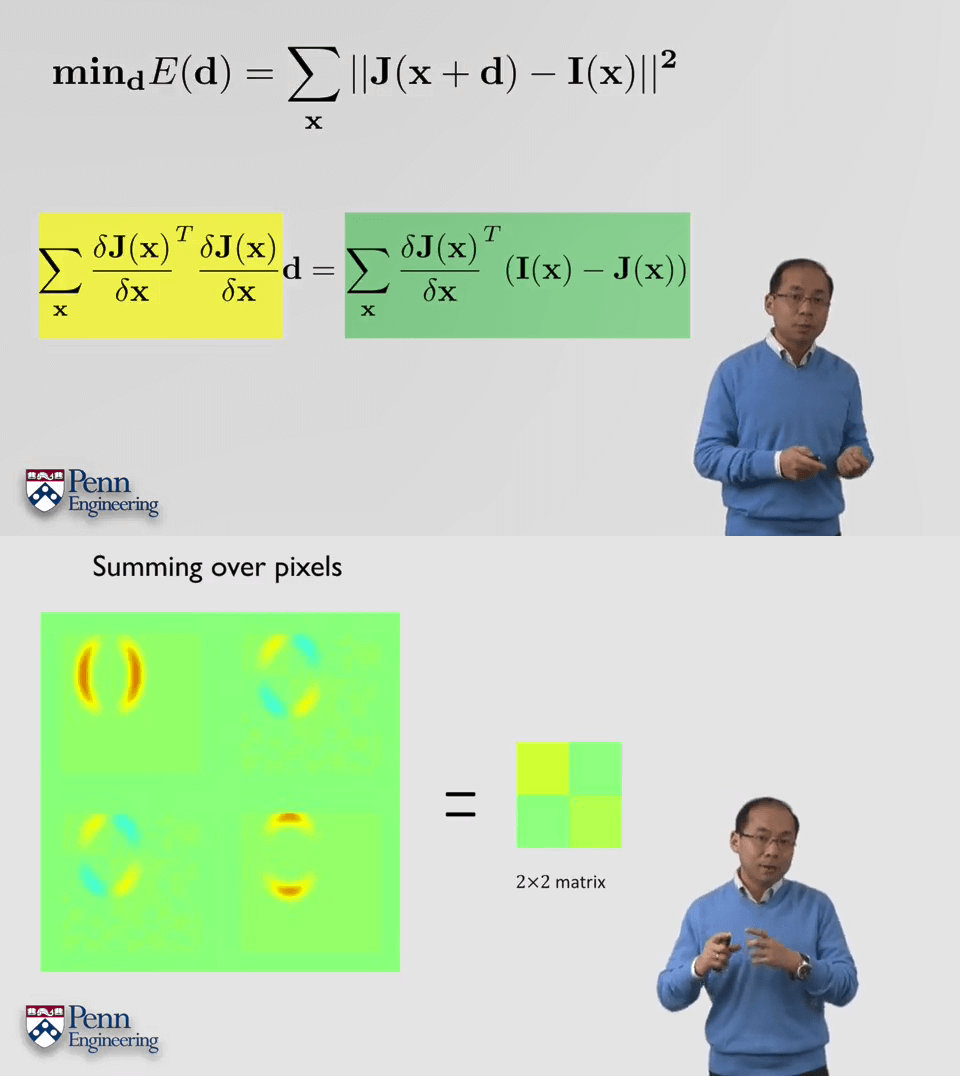
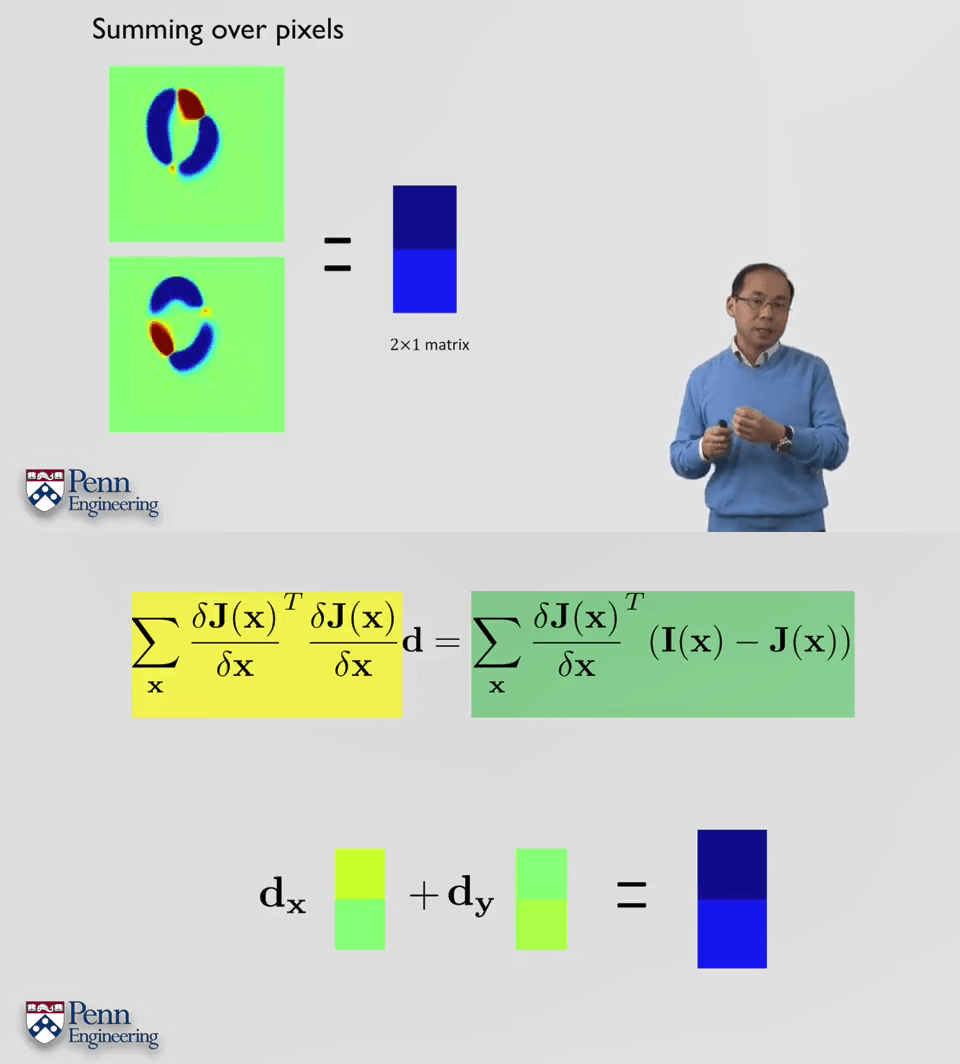
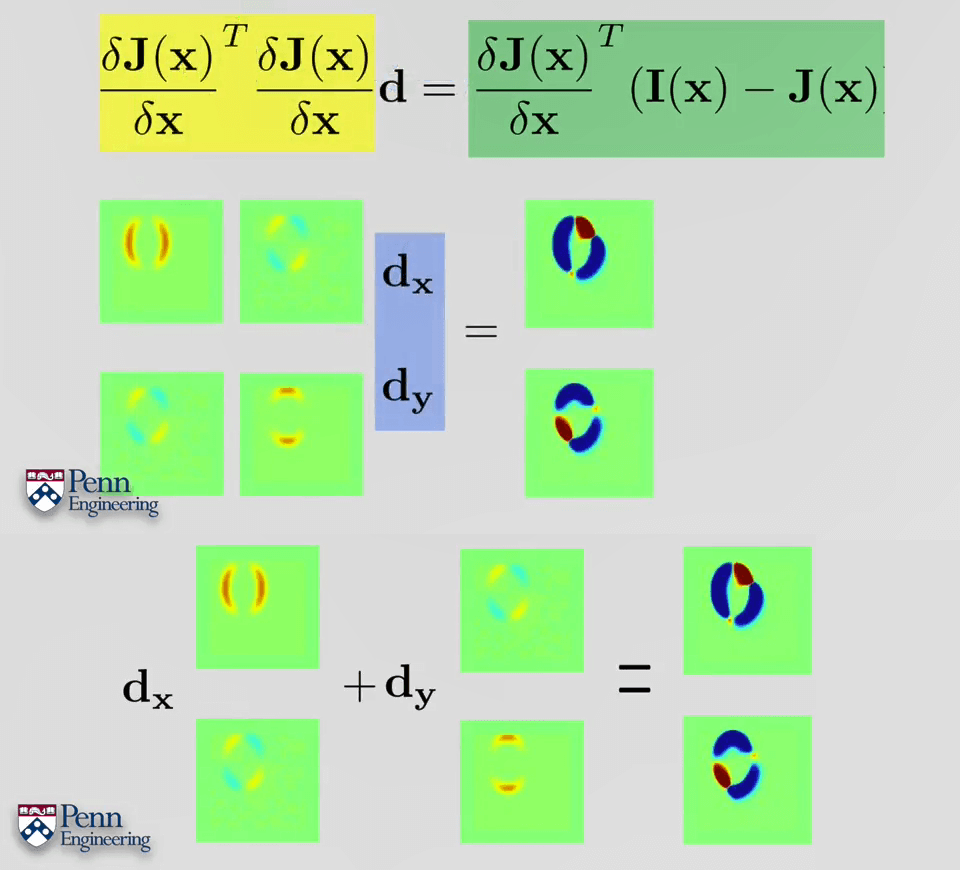
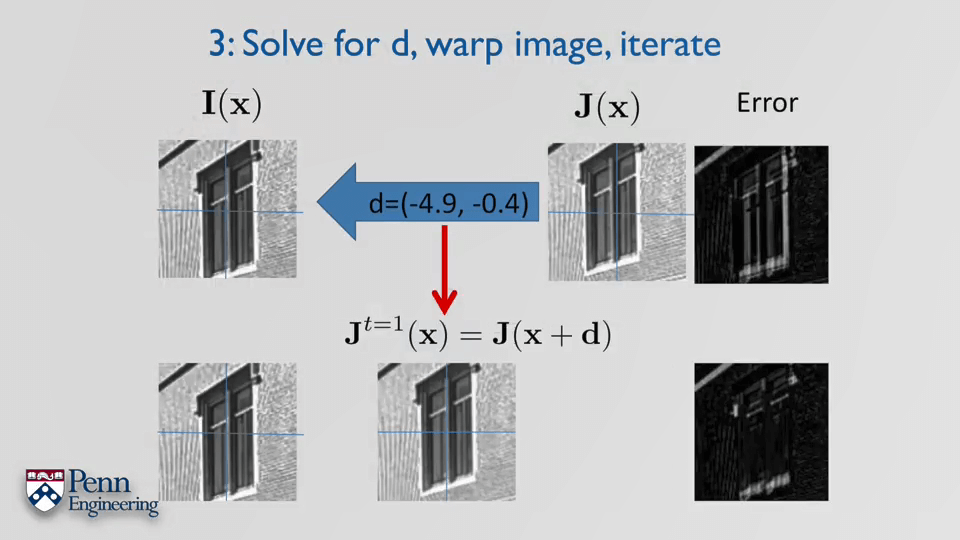
第三步,迭代计算。
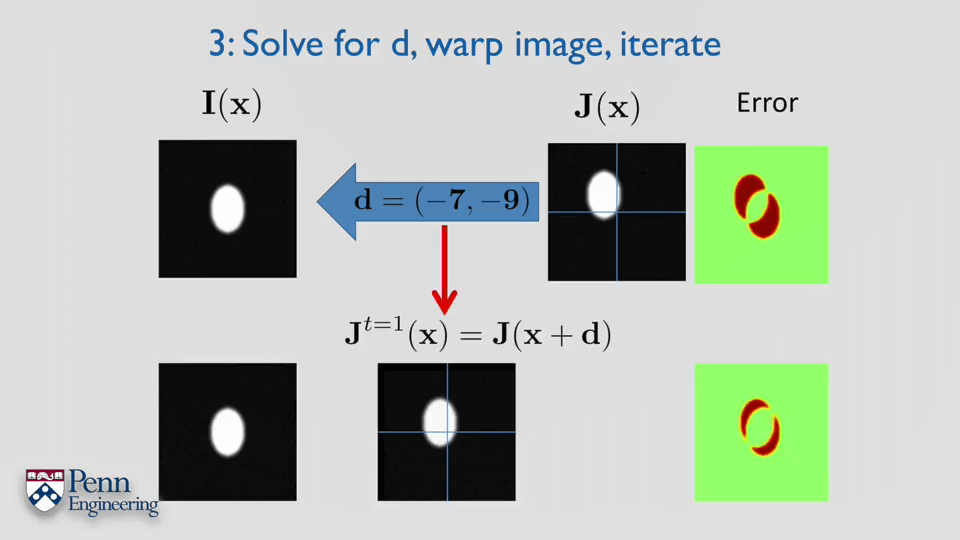
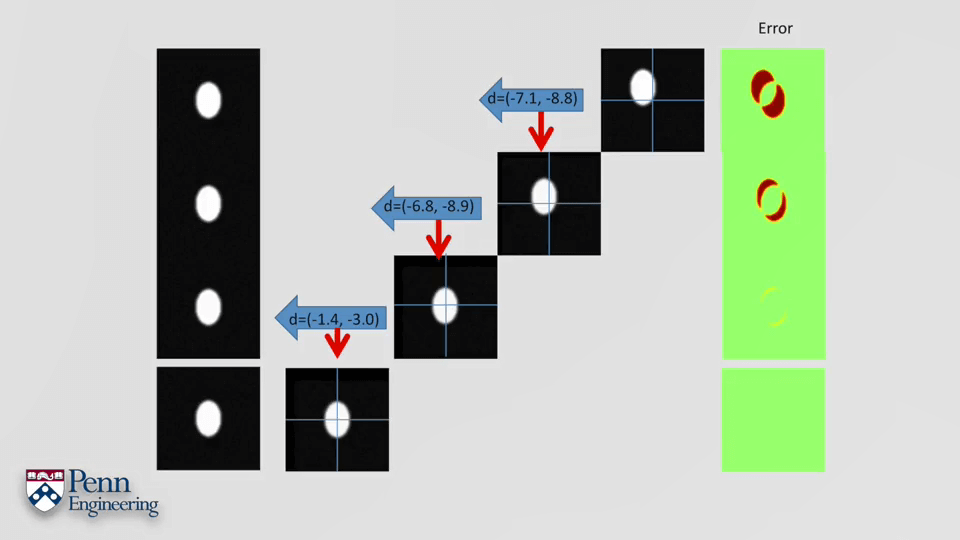
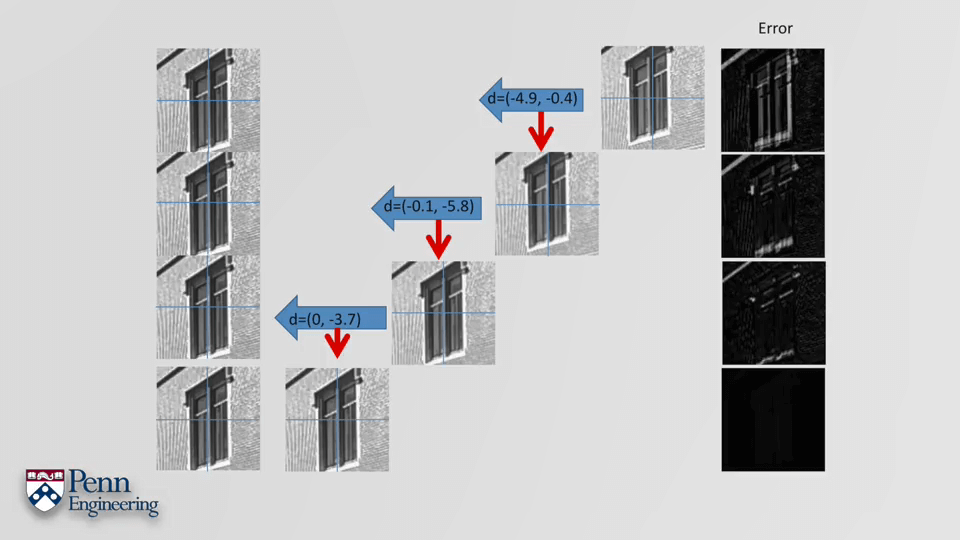
最后,以刚刚提到的窗口图片为例,步骤如下。

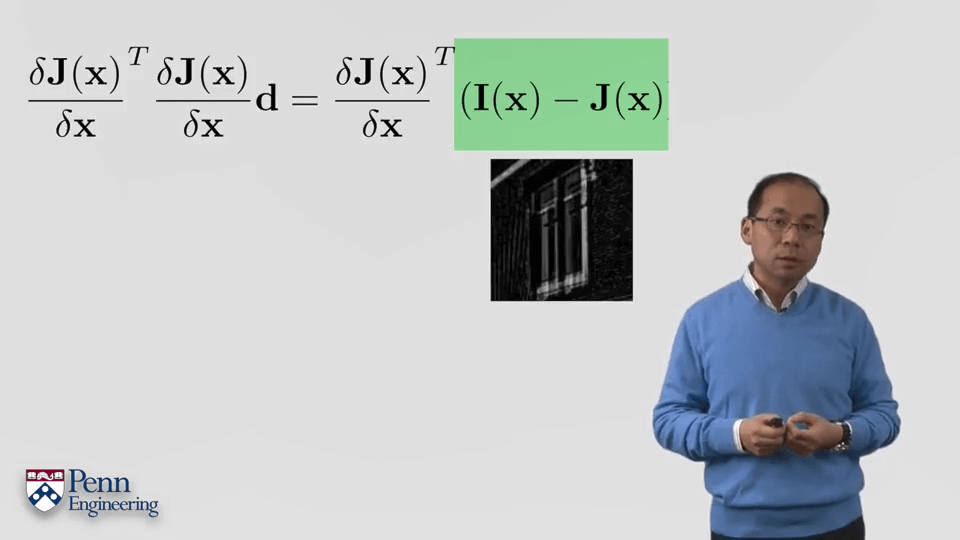
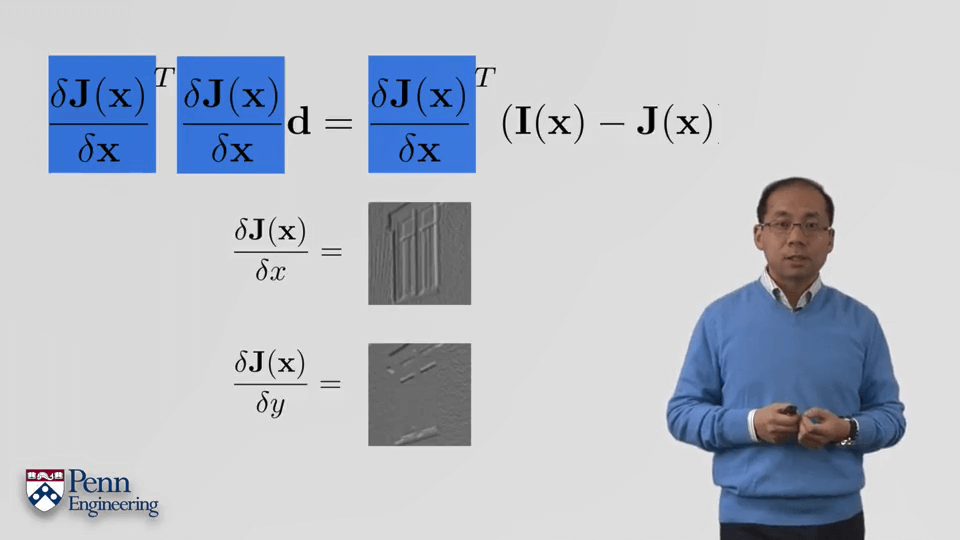
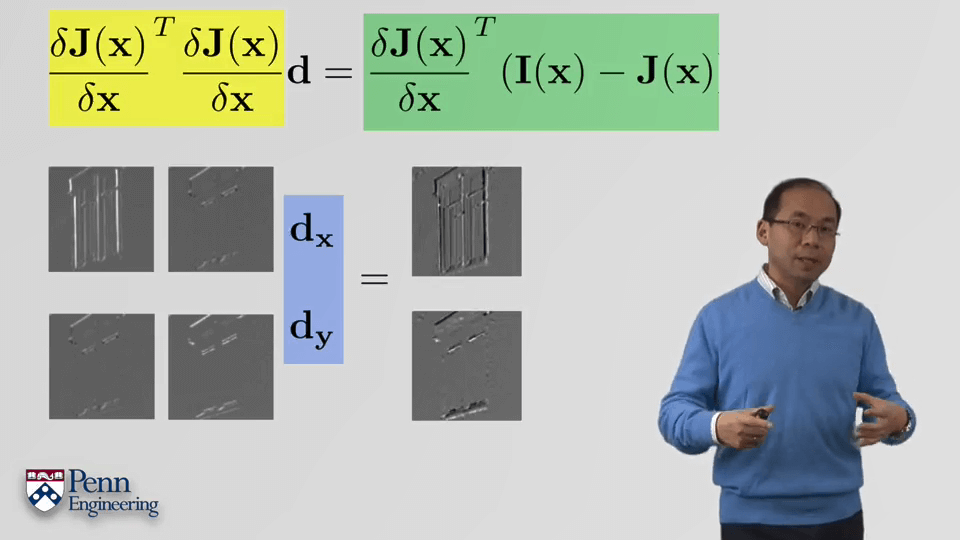
2.3D Velocities from Optical Flow
在上面,通过优化的手段获得了两帧之间对应点的光流关系,那么下面就可以利用光流来估计3D速度了。



 几种常见的运动对应的光流变化情况。
几种常见的运动对应的光流变化情况。
光流向量的长度如下图所示。
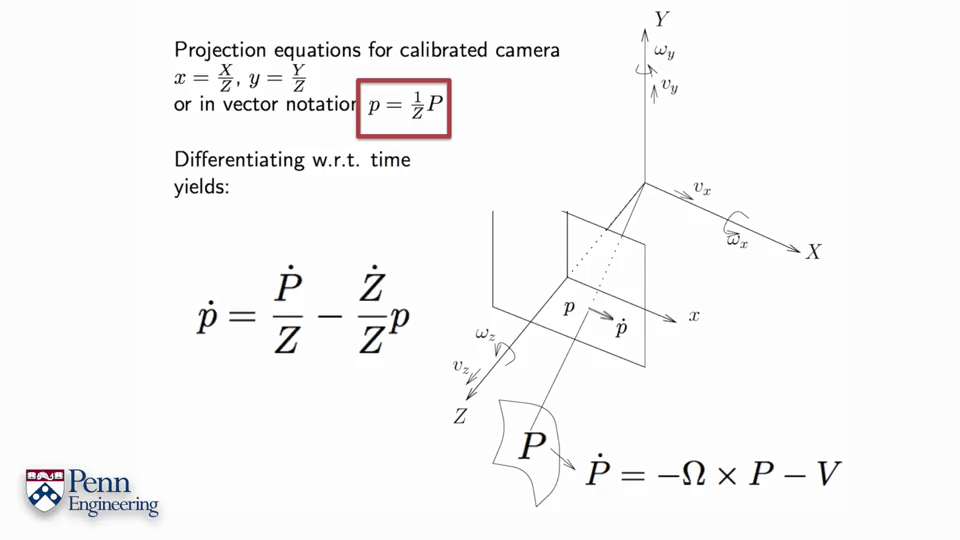 对于光流场向量可以分为平移部分和选择部分。
对于光流场向量可以分为平移部分和选择部分。

 如果有3个不共线的光流向量和深度,就可以基于6个式子解算3D速度。
如果有3个不共线的光流向量和深度,就可以基于6个式子解算3D速度。






对于既有平移又有旋转的混合情况。


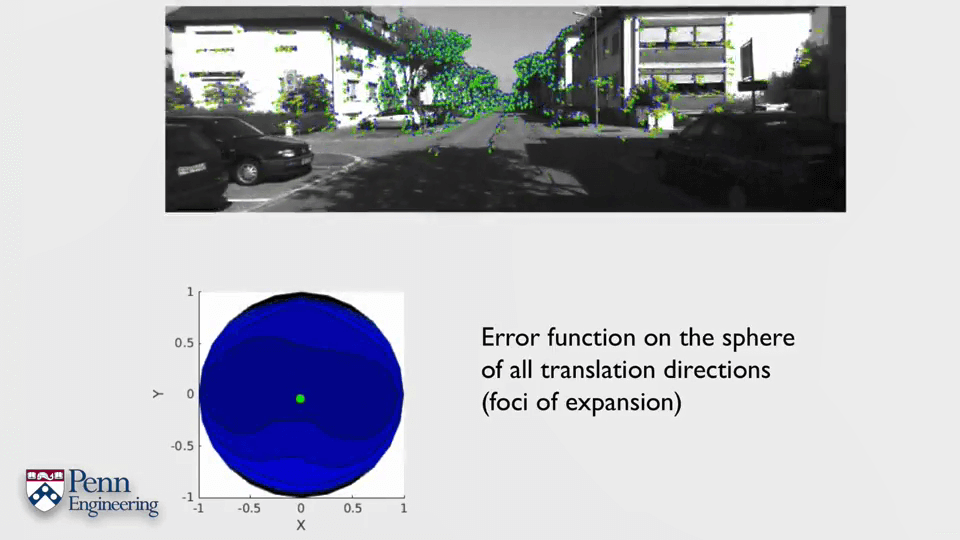
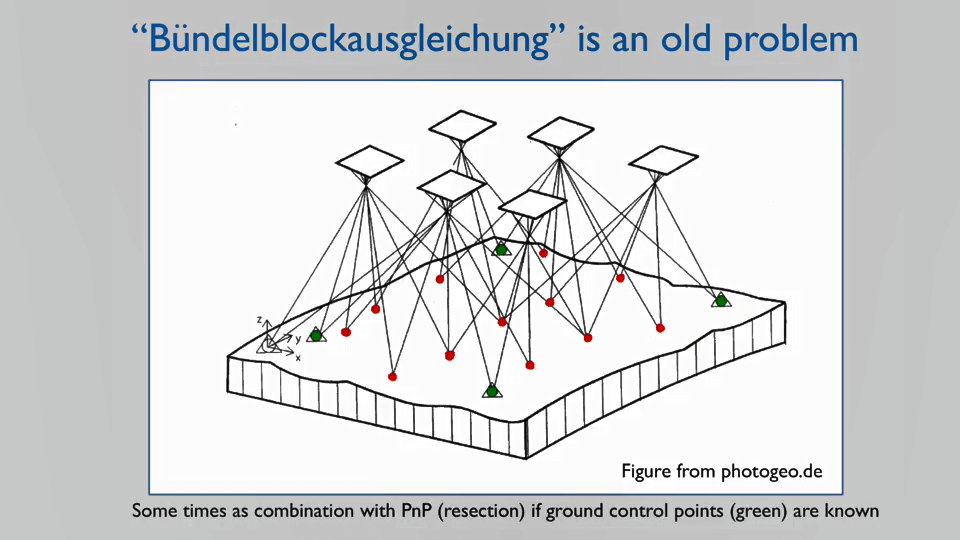
3.3D Motion and Structure from Multiple Views





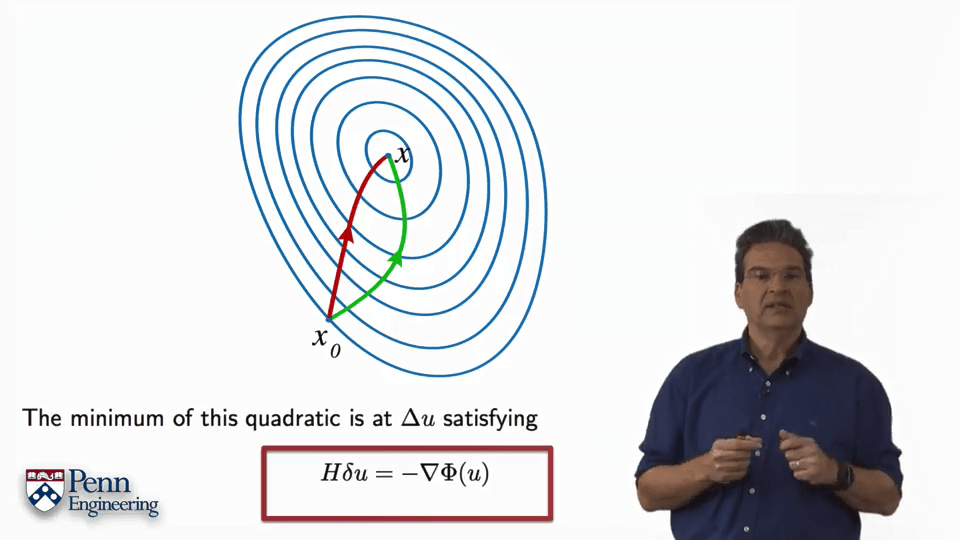



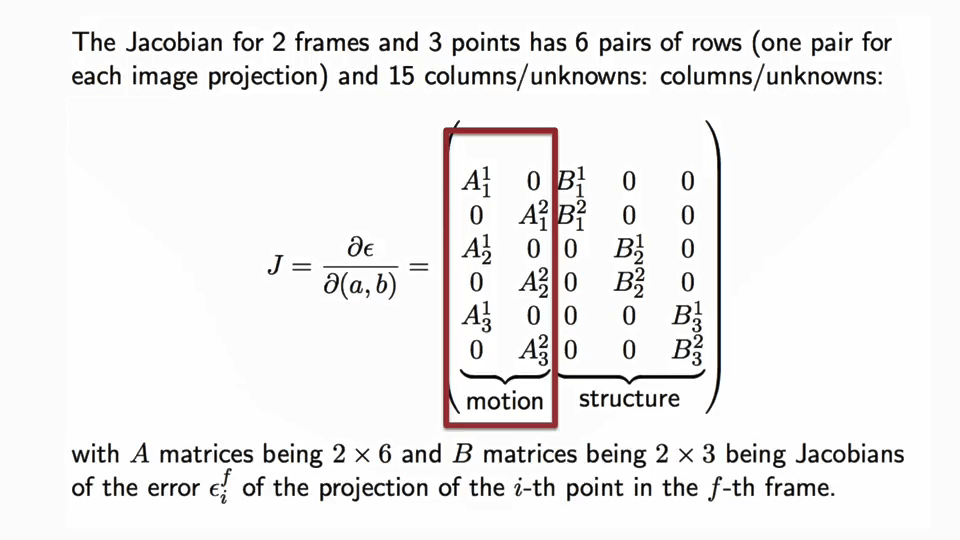
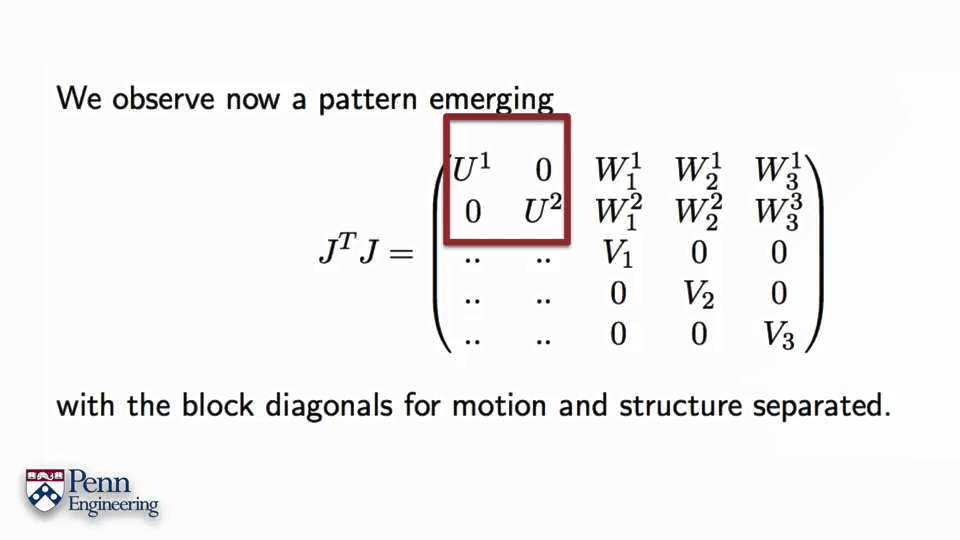



本文作者原创,未经许可不得转载,谢谢配合
