- 1.Course Introduction
- 2.Week 1 Introduction
- 3.1D Gaussian Distribution
- 4.Maximum Likelihood Estimate(MLE)
- 5.Multivariate Gaussian Distribution
- 6.MLE of Multivariate Gaussian
- 7.Gaussian Mixture Model
- 8.GMM Parameter Estimation via EM
- 9.EM Algorithm
本篇博客是Coursera上宾大的《Robotics:Estimation and Learning》的笔记,课程网址是这里。全篇笔记截图较多,建议在网速较好的情况下浏览或缓冲等待一会后再阅读。
1.Course Introduction
 本门课的两个核心问题是estimation和learning,其中估计指的是从有噪声的、不确定的数据中进行估计,而学习指的是使用先验知识来提高在不确定状态下的表现。
本门课的两个核心问题是estimation和learning,其中估计指的是从有噪声的、不确定的数据中进行估计,而学习指的是使用先验知识来提高在不确定状态下的表现。
 对于机器人而言,不确定性主要来自于传感器噪声、对周围世界感知的缺失以及周围场景的动态变化这三个方面。为了解决这个不确定性问题,本门课程从概率建模(probabilistic modeling)与机器学习(mechine learning)两方面进行介绍。具体而言包含四个方面的内容。
对于机器人而言,不确定性主要来自于传感器噪声、对周围世界感知的缺失以及周围场景的动态变化这三个方面。为了解决这个不确定性问题,本门课程从概率建模(probabilistic modeling)与机器学习(mechine learning)两方面进行介绍。具体而言包含四个方面的内容。

2.Week 1 Introduction
本周课程主要内容如下。

3.1D Gaussian Distribution
 为什么是高斯分布?简单来说就是三点:一是高斯分布参数简单(只需要均值与方差即可唯一确定一个高斯分布),易于计算与理解;二是高斯分布本身有非常好的数学性质,如高斯分布的乘积仍然是高斯分布,无需担心分布性质改变;三是根据大数定律,任意随机变量的期望分布最终都是高斯分布。
为什么是高斯分布?简单来说就是三点:一是高斯分布参数简单(只需要均值与方差即可唯一确定一个高斯分布),易于计算与理解;二是高斯分布本身有非常好的数学性质,如高斯分布的乘积仍然是高斯分布,无需担心分布性质改变;三是根据大数定律,任意随机变量的期望分布最终都是高斯分布。
具体而言,高斯分布由一个标量系数乘以一个指数部分组成,如下图所示。当μ=0,σ2=1的时候称为Standard Normal Distribution(zero mean and univariance)。
 标准正态分布如下图所示。
标准正态分布如下图所示。
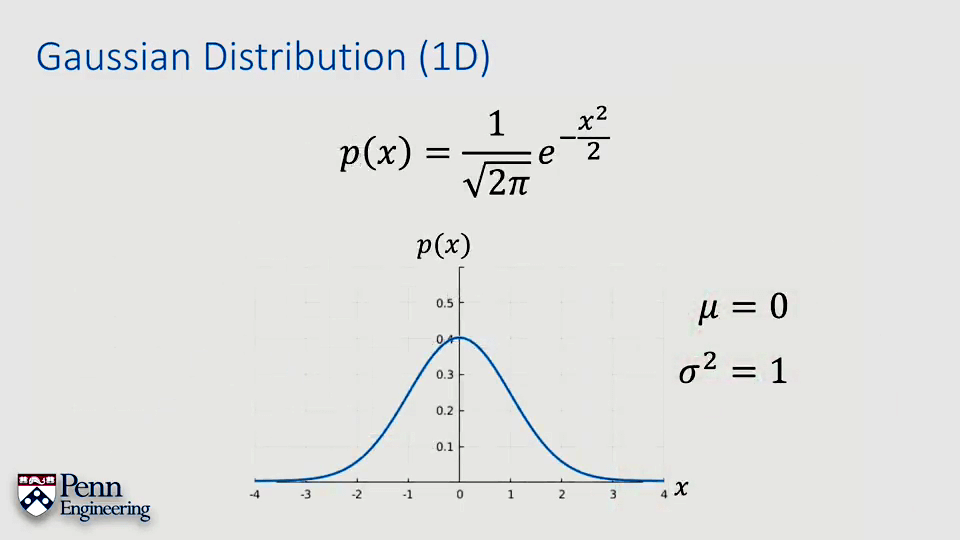 这个图应该并不陌生,从初中开始就见过了。简单再说一下需要注意的几个点。1.x距离均值越远概率越小,这是由于指数函数中x前面的负号导致的。2.指数部分前面的系数,为什么是这个奇怪的数字。因为这个函数是一个概率分布函数(PDF,probability density function),也就是说曲线下的面积积分应该为1。下面展示了均值与方差对于高斯曲线的影响。
这个图应该并不陌生,从初中开始就见过了。简单再说一下需要注意的几个点。1.x距离均值越远概率越小,这是由于指数函数中x前面的负号导致的。2.指数部分前面的系数,为什么是这个奇怪的数字。因为这个函数是一个概率分布函数(PDF,probability density function),也就是说曲线下的面积积分应该为1。下面展示了均值与方差对于高斯曲线的影响。
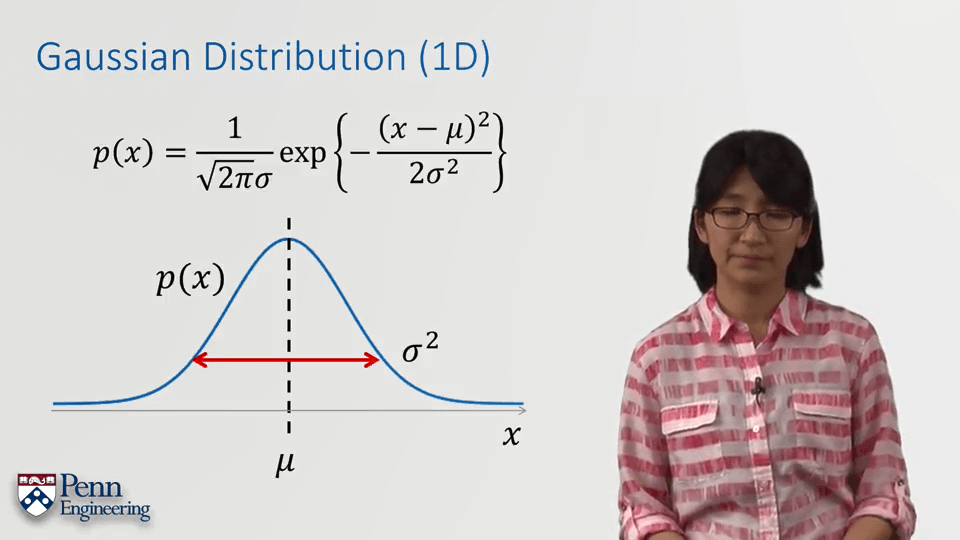 均值仅决定函数的中心位置,不会改变曲线的形状;方差仅决定函数的形状,不会改变曲线的位置,方差越大,曲线越矮。
均值仅决定函数的中心位置,不会改变曲线的形状;方差仅决定函数的形状,不会改变曲线的位置,方差越大,曲线越矮。
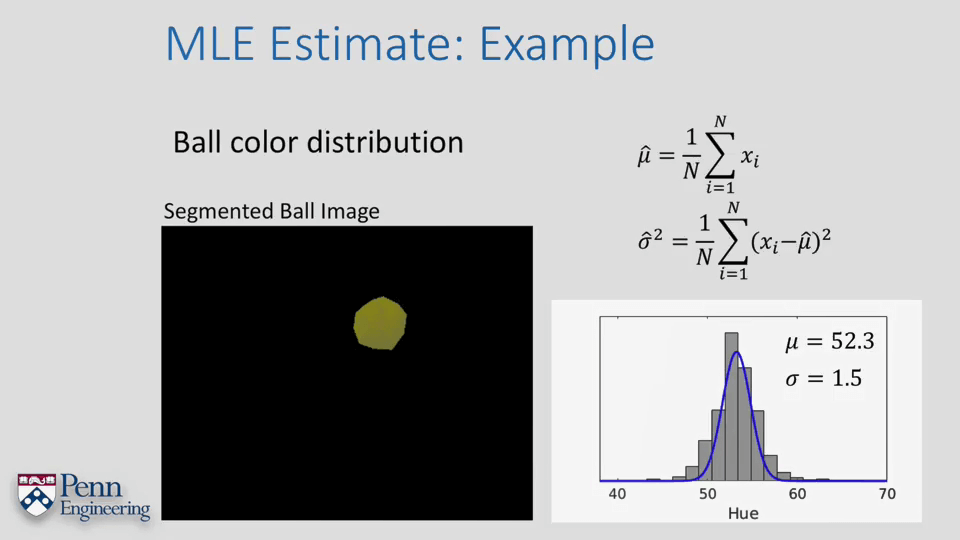
一个小例子:在HSV色彩空间基于高斯分布识别指定颜色物体。
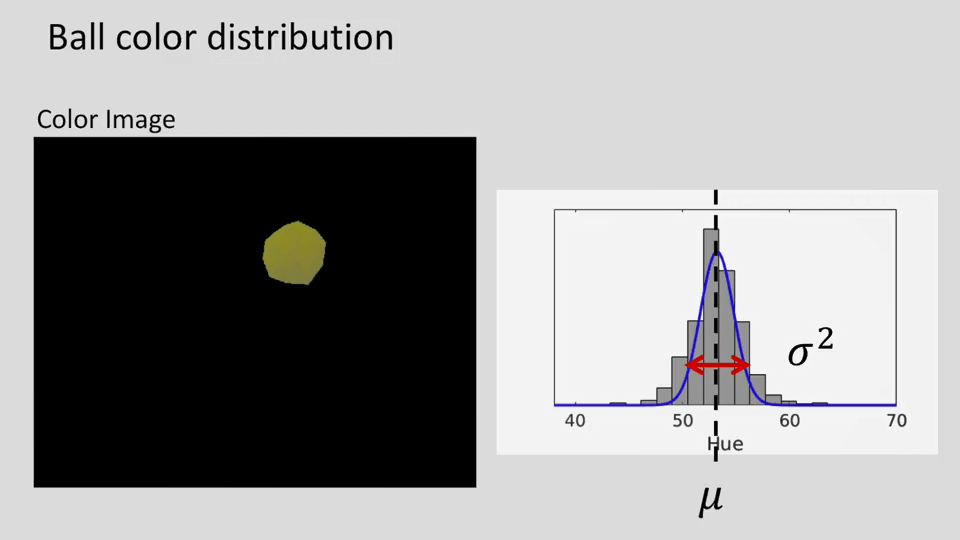 简单来说就是通过HSV色彩空间里的Hue通道进行颜色判别。首先获得目标区域颜色在Hue通道里的分布范围,如上图所示,然后基于这个分布得到一个高斯分布。这个高斯分布即可以认为是能够反映特定颜色的。这样,当有新的颜色需要判断时,我们只需要获取该颜色的Hue值,即可以得到该颜色是目标颜色的概率。进一步设置阈值,即可以判断该颜色是否为目标颜色。其实这个例子其实在之前OpenCV学习笔记中已经实现过类似的了,只不过那个时候只是用的简单的阈值判断。而现在通过使用高斯分布进行判断。
简单来说就是通过HSV色彩空间里的Hue通道进行颜色判别。首先获得目标区域颜色在Hue通道里的分布范围,如上图所示,然后基于这个分布得到一个高斯分布。这个高斯分布即可以认为是能够反映特定颜色的。这样,当有新的颜色需要判断时,我们只需要获取该颜色的Hue值,即可以得到该颜色是目标颜色的概率。进一步设置阈值,即可以判断该颜色是否为目标颜色。其实这个例子其实在之前OpenCV学习笔记中已经实现过类似的了,只不过那个时候只是用的简单的阈值判断。而现在通过使用高斯分布进行判断。
4.Maximum Likelihood Estimate(MLE)
如上所述,要想确定一个高斯分布,需要均值与方差两个参数。如何根据一堆观测数据来最优地估计对应的高斯分布便是这一小节要关注的问题。为了解决这个问题,就需要用到MLE(最大似然估计)。
 也就是说,我们关注的是在给定一组观测的前提下能够获得最大可能性的那个模型的参数(obtaining the parameters of our model that maximizes the likelihood of a given set of observations)。因此从某种程度上来说也可以看作是一个优化问题。如下。
也就是说,我们关注的是在给定一组观测的前提下能够获得最大可能性的那个模型的参数(obtaining the parameters of our model that maximizes the likelihood of a given set of observations)。因此从某种程度上来说也可以看作是一个优化问题。如下。
 这里我们要最大化的这个似然函数就是所有观测数据的联合概率(The likelihood function we are going to maximize is the joint probability of all the data)。显然如果各观测间不独立,这个联合概率密度并不容易求解。因此我们假设各个观测之间独立,则联合概率可以写成各概率的乘积。因此我们的优化目标函数就由上图中的第一个式子变成了最后一个式子。
这里我们要最大化的这个似然函数就是所有观测数据的联合概率(The likelihood function we are going to maximize is the joint probability of all the data)。显然如果各观测间不独立,这个联合概率密度并不容易求解。因此我们假设各个观测之间独立,则联合概率可以写成各概率的乘积。因此我们的优化目标函数就由上图中的第一个式子变成了最后一个式子。
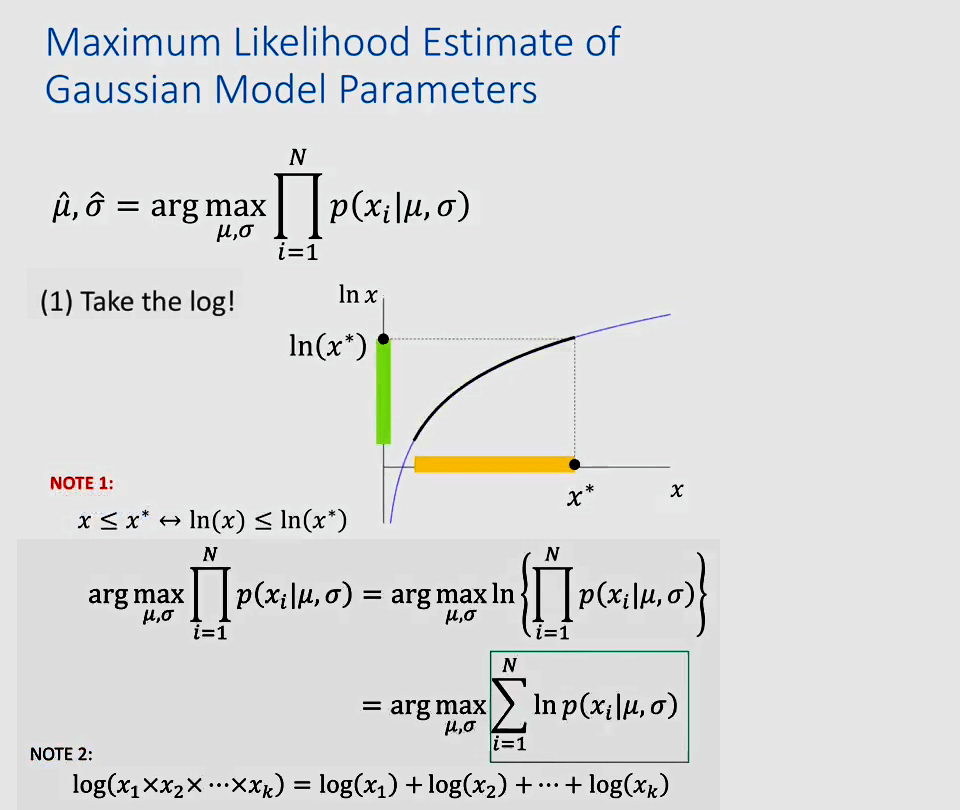 进一步,对于这个式子我们还可以进行操作。首先是对其取对数,利用对数性质。由于对数函数单增,因此对原式取对数并不会改变结果。另一方面,根据对数乘法的性质,可以将目标函数中的连乘写成累加(这一步对后续求导简化很大)。进一步,我们根据高斯分布本身的定义式,带入目标函数可以进一步化简。
进一步,对于这个式子我们还可以进行操作。首先是对其取对数,利用对数性质。由于对数函数单增,因此对原式取对数并不会改变结果。另一方面,根据对数乘法的性质,可以将目标函数中的连乘写成累加(这一步对后续求导简化很大)。进一步,我们根据高斯分布本身的定义式,带入目标函数可以进一步化简。
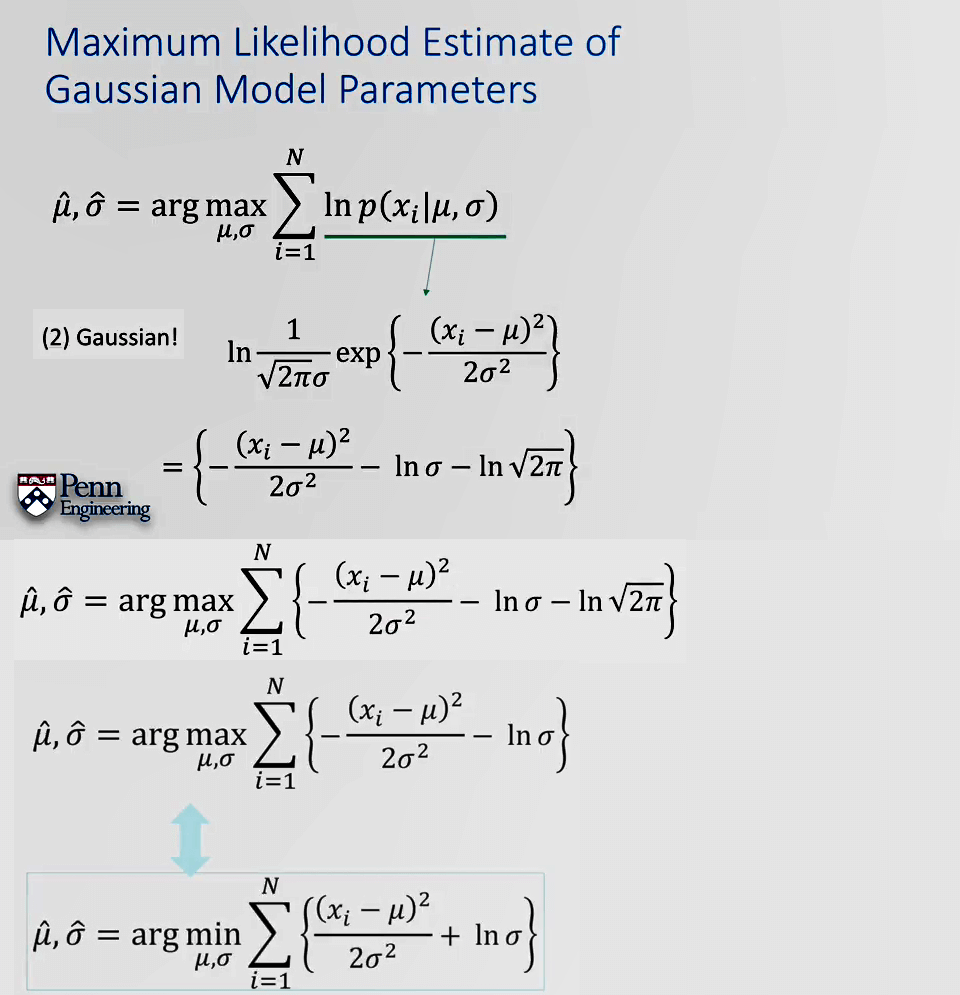 由于高斯函数里本身有指数项,因此再取对数,就可以得到上图中第三行的式子,我们的优化目标函数就变成了第四行的式子。由于常数项不影响结果,所以直接去除。最后,为了方便,我们对目标函数取负数,这样就从求最大值变成了求最小值。得到了最终的优化目标函数如最后一行所示。
由于高斯函数里本身有指数项,因此再取对数,就可以得到上图中第三行的式子,我们的优化目标函数就变成了第四行的式子。由于常数项不影响结果,所以直接去除。最后,为了方便,我们对目标函数取负数,这样就从求最大值变成了求最小值。得到了最终的优化目标函数如最后一行所示。
 对于这个式子,不妨记目标函数为J,这样J先对μ求偏导,并使其导数为0,先求得μ的估计,然后将估计的μ代回,再求σ的偏导并使其导数为0。最终可以得到高斯分布的MLE的解为:
对于这个式子,不妨记目标函数为J,这样J先对μ求偏导,并使其导数为0,先求得μ的估计,然后将估计的μ代回,再求σ的偏导并使其导数为0。最终可以得到高斯分布的MLE的解为:
 毫无意外,其实这就是不能再熟悉的均值与方差的定义式了。单就这个结果本身而言没什么要说的,更重要的是需要理解前面的一系列的推导和求解过程。
毫无意外,其实这就是不能再熟悉的均值与方差的定义式了。单就这个结果本身而言没什么要说的,更重要的是需要理解前面的一系列的推导和求解过程。
另外,回到上面的那个颜色分割小例子。我们可以根据Hue的值的分布分别计算出均值与方差,它们俩共同就构成了一个高斯分布。
5.Multivariate Gaussian Distribution
上面说的都是单变量高斯分布,下面介绍的是多变量(multivariate)高斯分布。一维高斯可以叫做Univariate Gaussian。
 与单变量高斯分布类似的,x为自变量,不同的是x这里为向量而非标量,同理μ也是。Σ为协方差矩阵,主对角线为方差。这里还是以识别有颜色的小球为例,不同的是这次不用HSV空间,而用RGB色彩空间。
与单变量高斯分布类似的,x为自变量,不同的是x这里为向量而非标量,同理μ也是。Σ为协方差矩阵,主对角线为方差。这里还是以识别有颜色的小球为例,不同的是这次不用HSV空间,而用RGB色彩空间。
 为了更加直观理解多变量高斯分布,这里以0均值的2D高斯分布为例。
为了更加直观理解多变量高斯分布,这里以0均值的2D高斯分布为例。
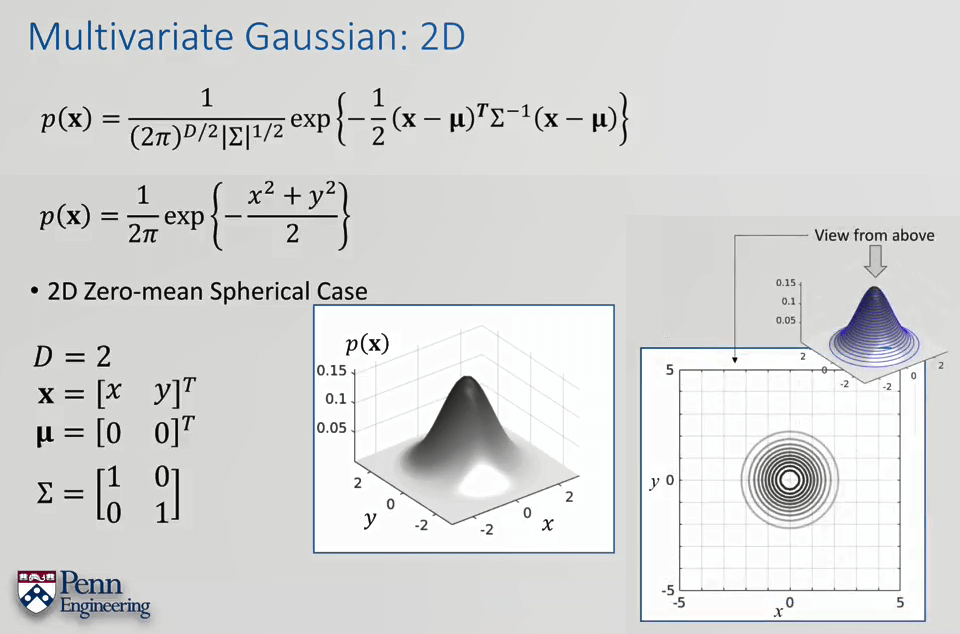 可以看出这是一个山峰型的曲面,如果俯视看的话就是一圈圈的同心圆,表明相同概率。与1D高斯类似,均值只影响曲面位置,不影响形状;协方差矩阵只影响形状不影响位置。
可以看出这是一个山峰型的曲面,如果俯视看的话就是一圈圈的同心圆,表明相同概率。与1D高斯类似,均值只影响曲面位置,不影响形状;协方差矩阵只影响形状不影响位置。
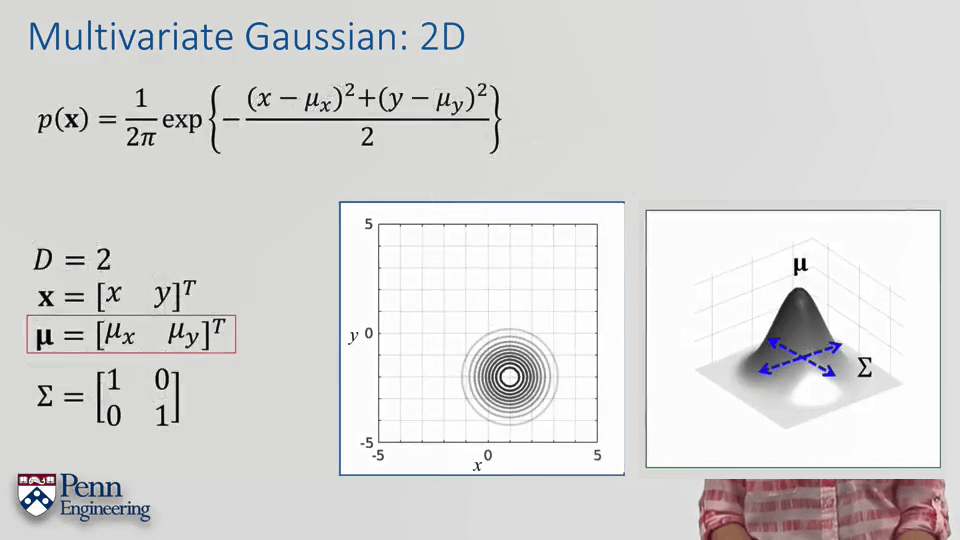
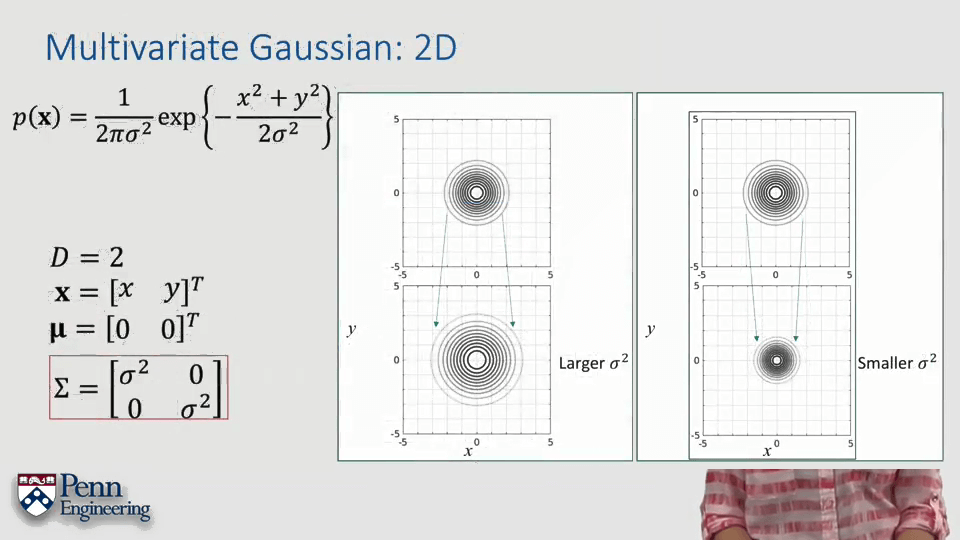 此外,协方差矩阵也带来了一些1D高斯分布没有的性质,从而使得曲面不再是标准的,而被“压扁了”。
此外,协方差矩阵也带来了一些1D高斯分布没有的性质,从而使得曲面不再是标准的,而被“压扁了”。
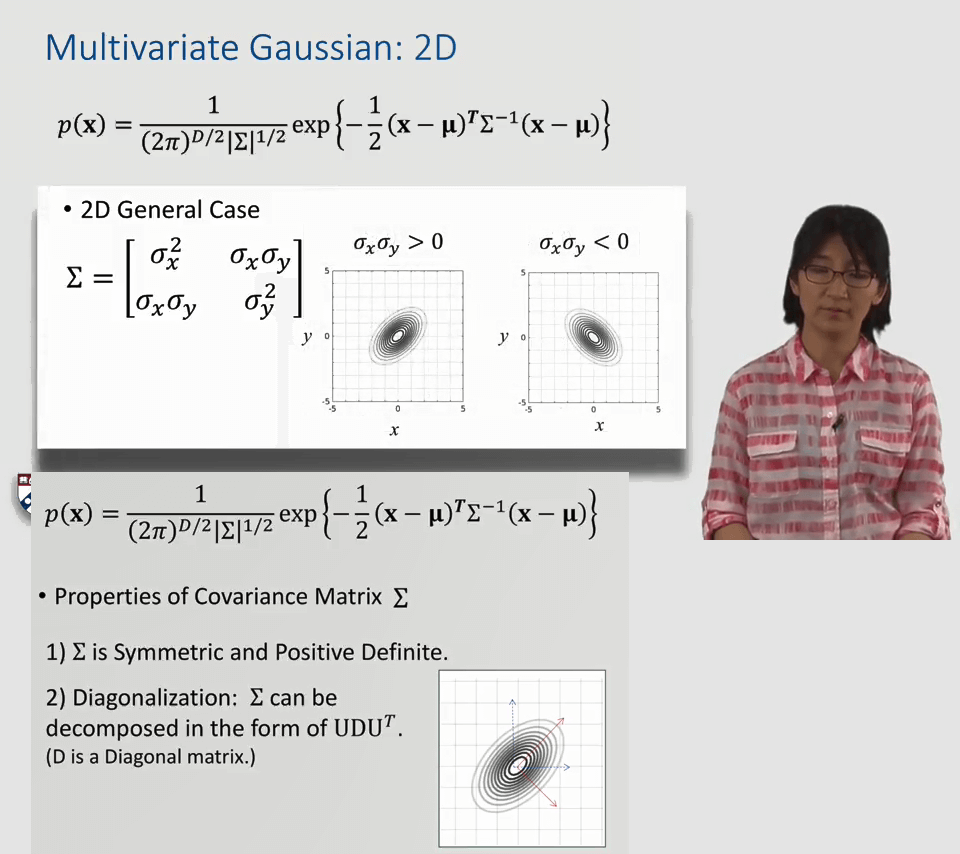 协方差矩阵本身也有一些独特性质:1.协方差矩阵是对称的,且其特征值一定为正。2.协方差矩阵可以被分解为UDUT的形式。我们总是能够找到使得分布对称的坐标变换。
协方差矩阵本身也有一些独特性质:1.协方差矩阵是对称的,且其特征值一定为正。2.协方差矩阵可以被分解为UDUT的形式。我们总是能够找到使得分布对称的坐标变换。
6.MLE of Multivariate Gaussian
与1D高斯分布类似,上面介绍了多变量高斯分布,这一小节自然就要介绍该如何根据观测数据对多变量高斯分布的参数进行估计。与1D高斯类似的,多变量高斯同样由均值与方差决定。不同的是在多变量高斯中,均值不再是一个数而变成了向量,方差变成了协方差矩阵。我们使用相同的符号表示。
 和上面一样,由于目标函数是联合概率密度,直接不好处理,所以假设各观测之间相互独立,联合概率密度就可以写成乘积形式。
和上面一样,由于目标函数是联合概率密度,直接不好处理,所以假设各观测之间相互独立,联合概率密度就可以写成乘积形式。
 然后再对目标函数进行相同的两步操作:取对数与代入高斯分布式子,对目标函数进行简化。
然后再对目标函数进行相同的两步操作:取对数与代入高斯分布式子,对目标函数进行简化。
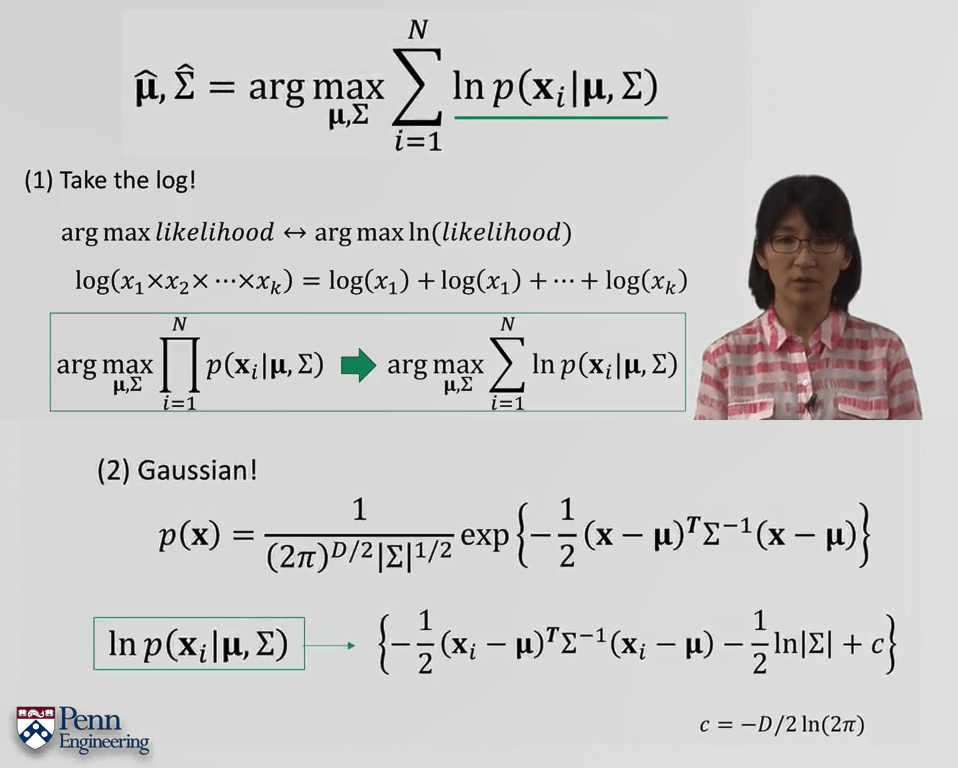 最后,对目标函数取负号,寻求最小值,求偏导求解。
最后,对目标函数取负号,寻求最小值,求偏导求解。
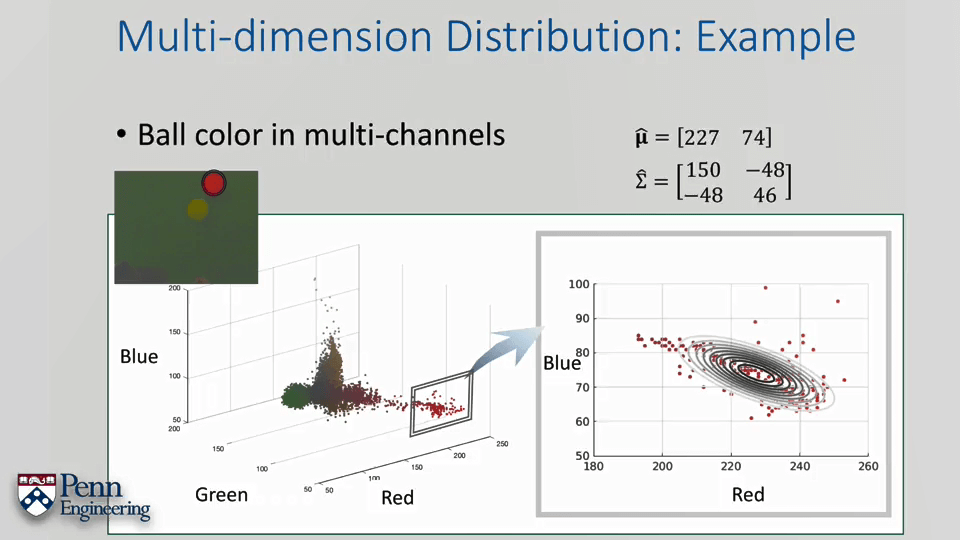
 最后还是那个彩色小球例子。
最后还是那个彩色小球例子。
7.Gaussian Mixture Model
上面说了那么多,1D高斯也好,多变量高斯也好,都是单一的高斯模型,从直观上来看就是只有一个峰(peak)。但很显然现实世界中的分布不可能总是如此简单,而是千奇百怪。因此单个高斯模型就无法满足需求了,而需要多个高斯模型叠加。如下图所示,单高斯模型只能拟合单峰、对称分布。对于多峰、非对称分布就显得有些力不从心。
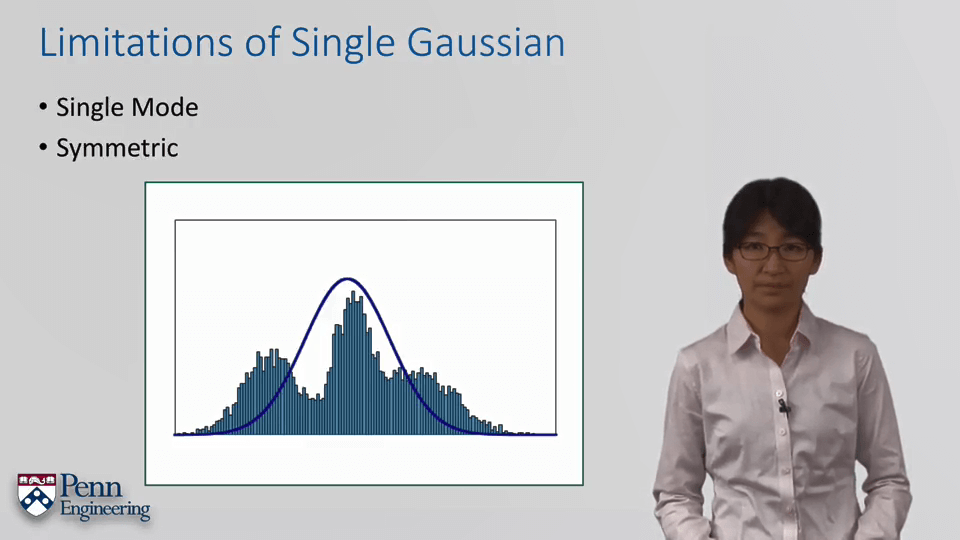 GMM简单可以理解为就是多个高斯分布之和,通过多个高斯分布的线性叠加组合,可以拟合出任意形状的分布。
GMM简单可以理解为就是多个高斯分布之和,通过多个高斯分布的线性叠加组合,可以拟合出任意形状的分布。
 但同时另一方面,GMM虽然可以拟合很复杂的分布,但代价也很昂贵。两者需要根据实际情况合理选择,没有绝对的好坏。
但同时另一方面,GMM虽然可以拟合很复杂的分布,但代价也很昂贵。两者需要根据实际情况合理选择,没有绝对的好坏。
还是彩色小球例子,我们以G和R通道为例表达这个红色的小球。我们可以有两种思路,一是按照多变量高斯来拟合,二是按照高斯混合来拟合。
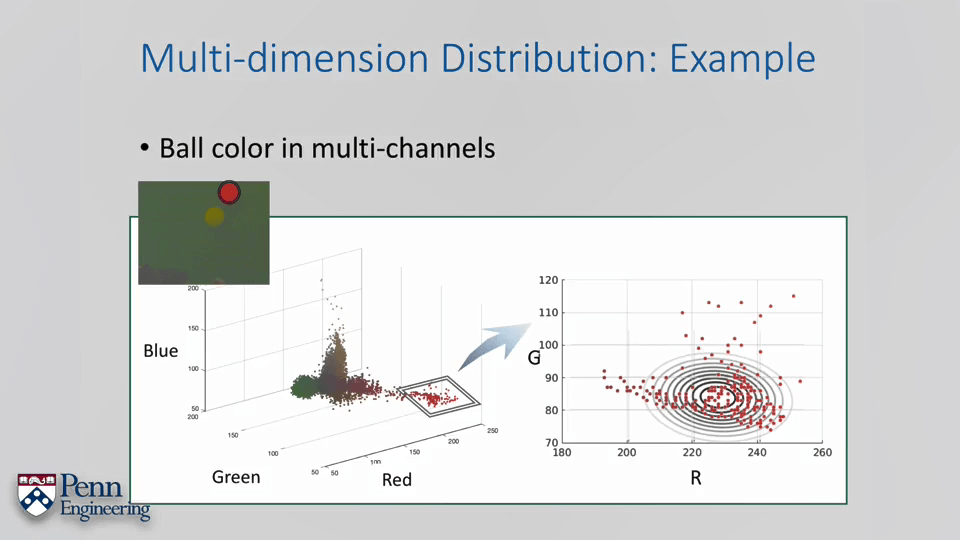
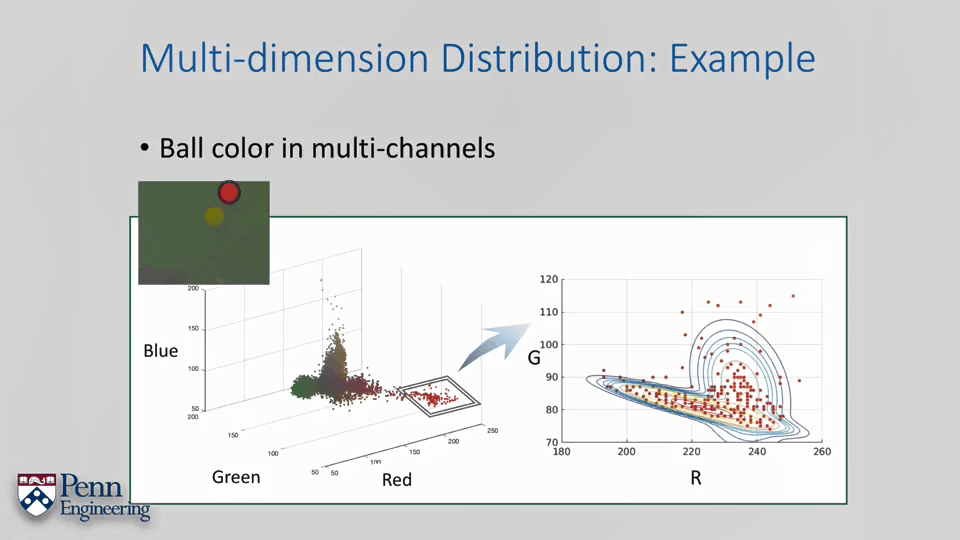 下面从数学角度给出GMM的定义。
下面从数学角度给出GMM的定义。
 可以看出GMM就是一系列具有不同均值与方差的高斯分布的加权和。所有加权系数都应该大于0,且所有系数之和应该为1。求和Σ上面的大K表示GMM包含的高斯成分的个数。如果不限制K的个数,那么GMM可以表示任意的分布,这也是GMM为什么如此强大的原因。但正如上面所说,GMM所需要的系数也很多。
可以看出GMM就是一系列具有不同均值与方差的高斯分布的加权和。所有加权系数都应该大于0,且所有系数之和应该为1。求和Σ上面的大K表示GMM包含的高斯成分的个数。如果不限制K的个数,那么GMM可以表示任意的分布,这也是GMM为什么如此强大的原因。但正如上面所说,GMM所需要的系数也很多。
 这也带来了一些副作用:例如很难估计参数,没有解析解;容易过拟合。
这也带来了一些副作用:例如很难估计参数,没有解析解;容易过拟合。
 在本门课中涉及的GMM,各成分之间等权,数值为1/K。
在本门课中涉及的GMM,各成分之间等权,数值为1/K。
最后注意多变量高斯和高斯混合模型的区别。多变量高斯不管变量有多少,终究只是一个高斯模型,进一步说就是只会有一个peak,不管均值、协方差怎么变,形状都还是钟形的曲面。而高斯混合模型的形状则会千奇百怪。可以理解为是多个高斯模型的线性组合。
8.GMM Parameter Estimation via EM
上面介绍了GMM,这一小节介绍如何基于期望最大化方法(Expectation-Maximization,EM)对GMM的参数进行估计。
 与前面参数估计类似,流程如下。
与前面参数估计类似,流程如下。
 但这里的问题就在于由于GMM包含多个高斯,因此并不能像之前那样进一步简化然后求偏导了,这直接导致了我们的目标函数不存在严密解析解,只能迭代求解。这里使用EM算法求解。
但这里的问题就在于由于GMM包含多个高斯,因此并不能像之前那样进一步简化然后求偏导了,这直接导致了我们的目标函数不存在严密解析解,只能迭代求解。这里使用EM算法求解。
 EM算法还需要其它一些参数,初始的参数估计以及隐变量z(latent variable)。既然是迭代,参数的初始估计自然无需多说,由于目标函数是非凸的,存在大量的局部极值,如果没有相对可靠的迭代初值很容易陷入局部最优解。另一个需要关注的是隐变量z,这是一个新的概念。
EM算法还需要其它一些参数,初始的参数估计以及隐变量z(latent variable)。既然是迭代,参数的初始估计自然无需多说,由于目标函数是非凸的,存在大量的局部极值,如果没有相对可靠的迭代初值很容易陷入局部最优解。另一个需要关注的是隐变量z,这是一个新的概念。
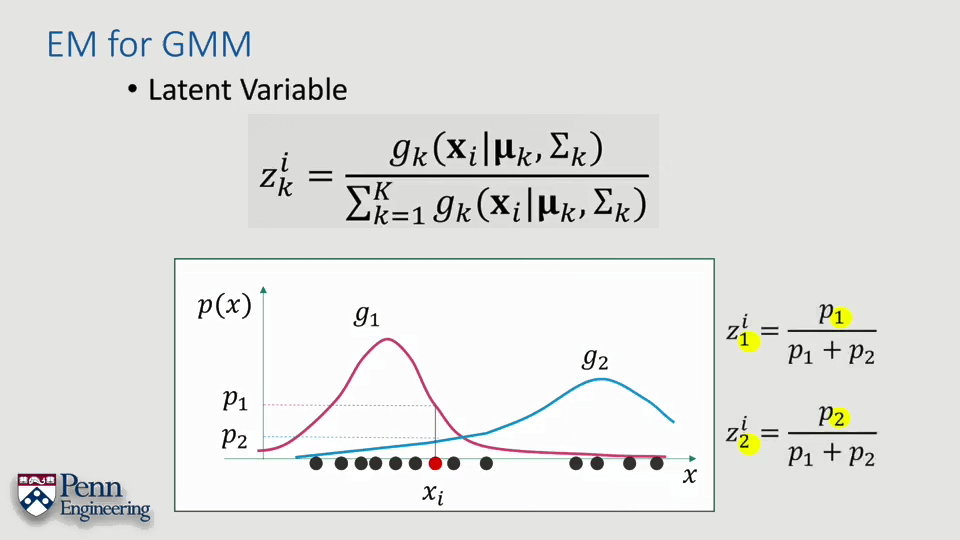 简单来说,隐变量z表达了在GMM中某个数据点属于某个高斯分布的概率(Z indicates the probability that the ith point is generated from the kth Gaussian components)。例如上图中的zi1表达了i这个数据点属于第1个高斯分布的概率。而且可以看到zi1要大于zi2,也就是说i这一点属于g1的概率更大。虽然定义式看起来比较复杂,但其实表达的意义是比较好理解的。根据其意义也可以很容易发现,如果把所有隐变量z加一起结果为1。
简单来说,隐变量z表达了在GMM中某个数据点属于某个高斯分布的概率(Z indicates the probability that the ith point is generated from the kth Gaussian components)。例如上图中的zi1表达了i这个数据点属于第1个高斯分布的概率。而且可以看到zi1要大于zi2,也就是说i这一点属于g1的概率更大。虽然定义式看起来比较复杂,但其实表达的意义是比较好理解的。根据其意义也可以很容易发现,如果把所有隐变量z加一起结果为1。
 进一步,我们可以将原始的均值与方差除以z,重新定义新的均值与方差。利用EM对GMM进行参数估计的流程如下。
进一步,我们可以将原始的均值与方差除以z,重新定义新的均值与方差。利用EM对GMM进行参数估计的流程如下。
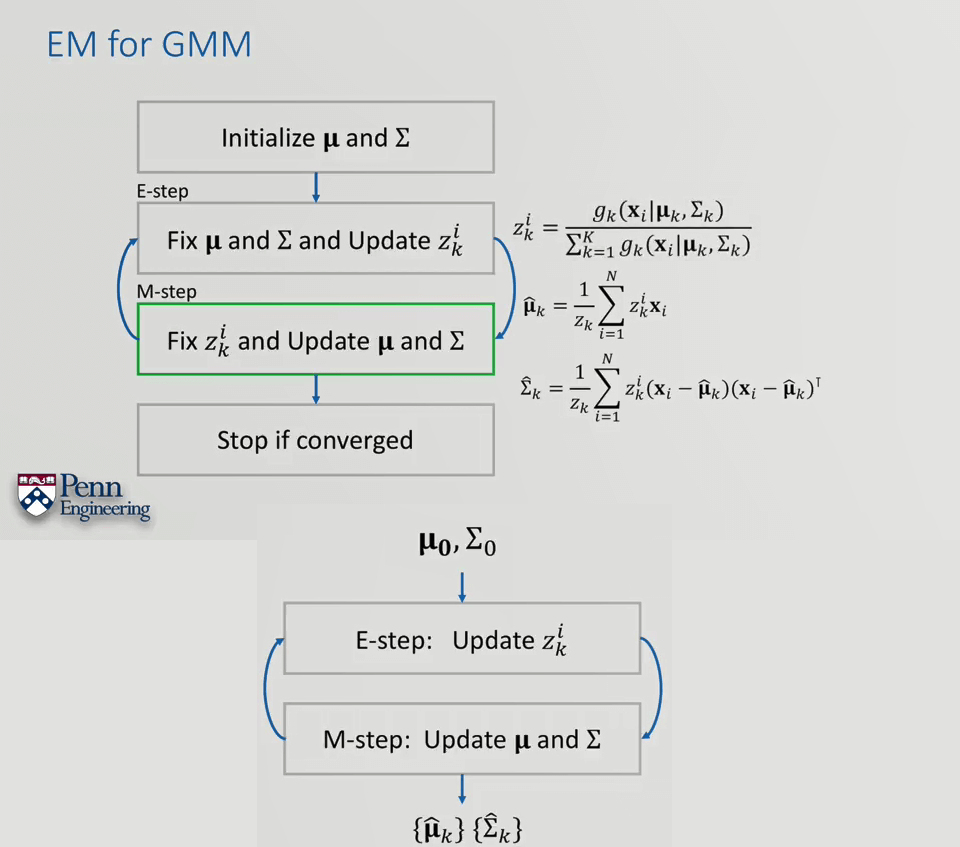
9.EM Algorithm
这一小节比较一般地介绍EM算法,主要包含如下图所示的三个方面。
 EM算法的主要思想可以用Jensen不等式解释,如下图所示。
EM算法的主要思想可以用Jensen不等式解释,如下图所示。
 对于凸函数而言,简单来说就是x1和x2所对应的函数值的均值总是大于等于x1和x2均值所对应的函数值(The mean of f(x1) and f(x2) is always larger than the function value of the mean)。进一步,可以推广上面的结论:
对于凸函数而言,简单来说就是x1和x2所对应的函数值的均值总是大于等于x1和x2均值所对应的函数值(The mean of f(x1) and f(x2) is always larger than the function value of the mean)。进一步,可以推广上面的结论:
 不等性质对于任意两个加权和也成立(第二行)。进一步,不等性质对于任意数量的点的加权和也成立(第三行)。上面的这些性质都是针对凸函数(convex)的,对于凹函数(concave)则把小于等于换成大于等于即可(第四行)。
不等性质对于任意两个加权和也成立(第二行)。进一步,不等性质对于任意数量的点的加权和也成立(第三行)。上面的这些性质都是针对凸函数(convex)的,对于凹函数(concave)则把小于等于换成大于等于即可(第四行)。
在我们需要处理的目标函数中,ln是凹的,所以等式变为下面的样子。利用Jensen不等式作为下界。
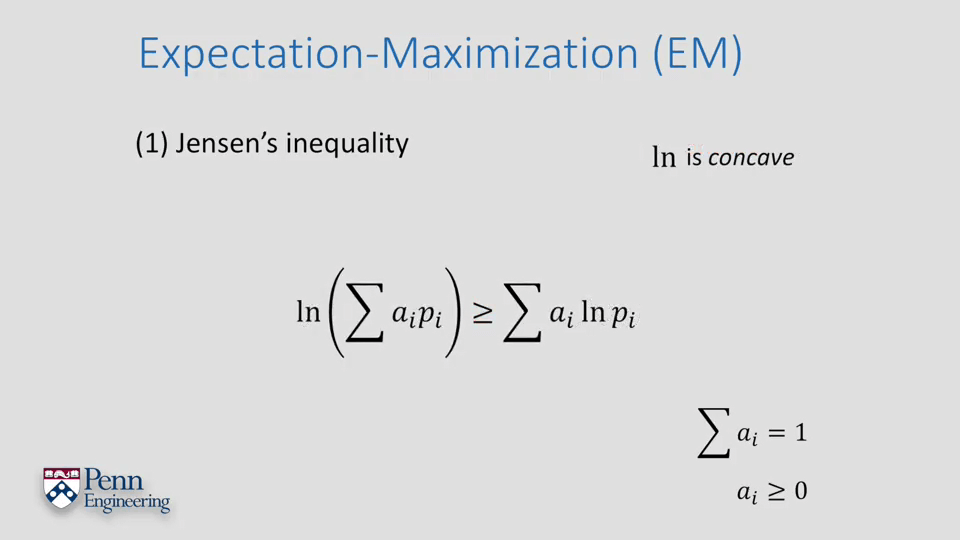
然后是隐变量z(latent variable)。



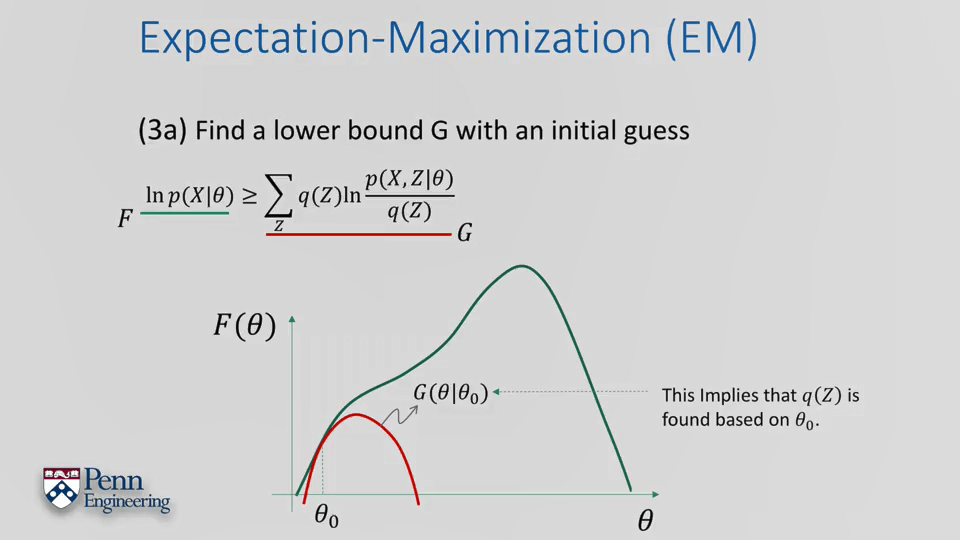
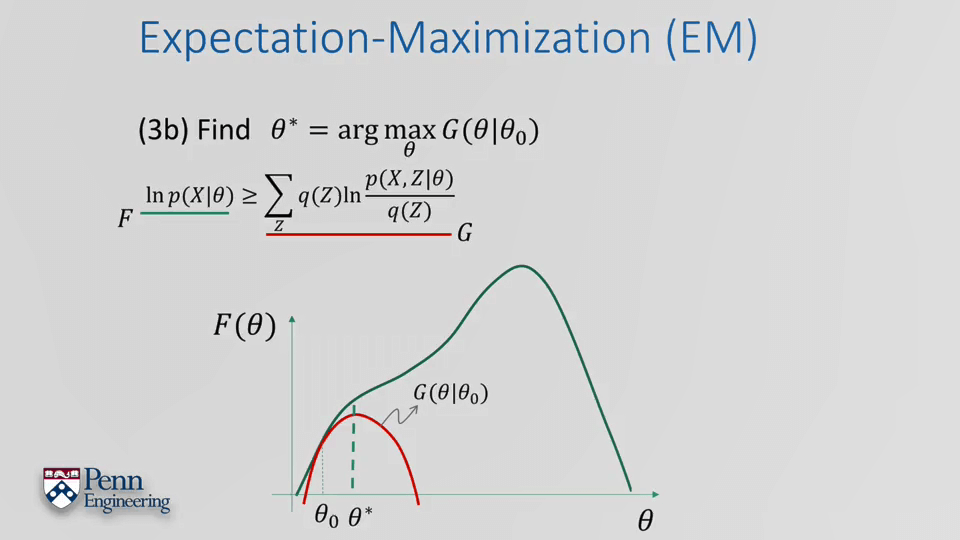
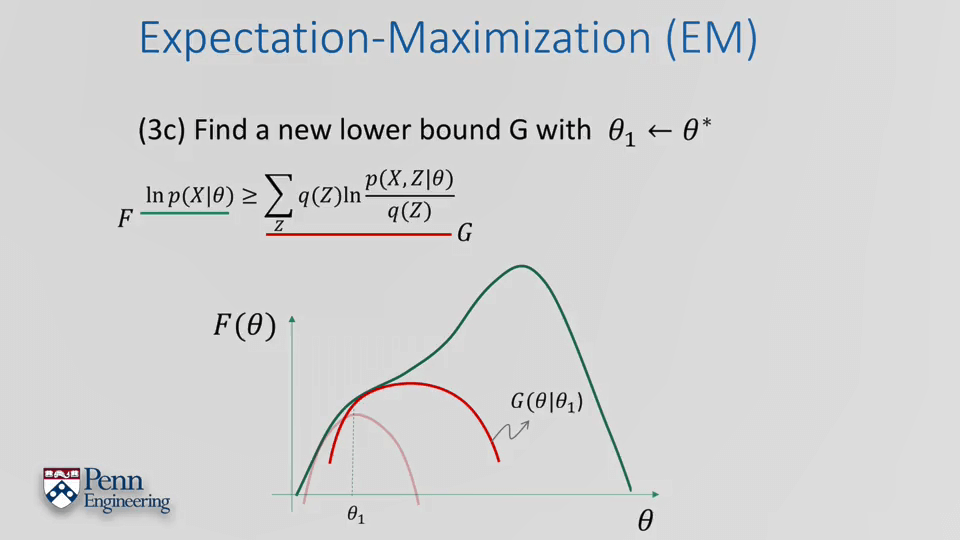
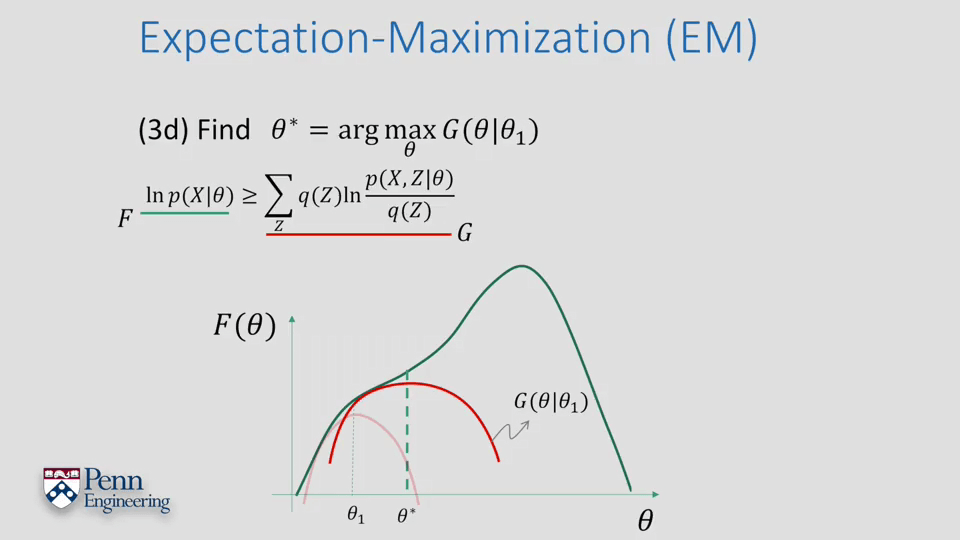
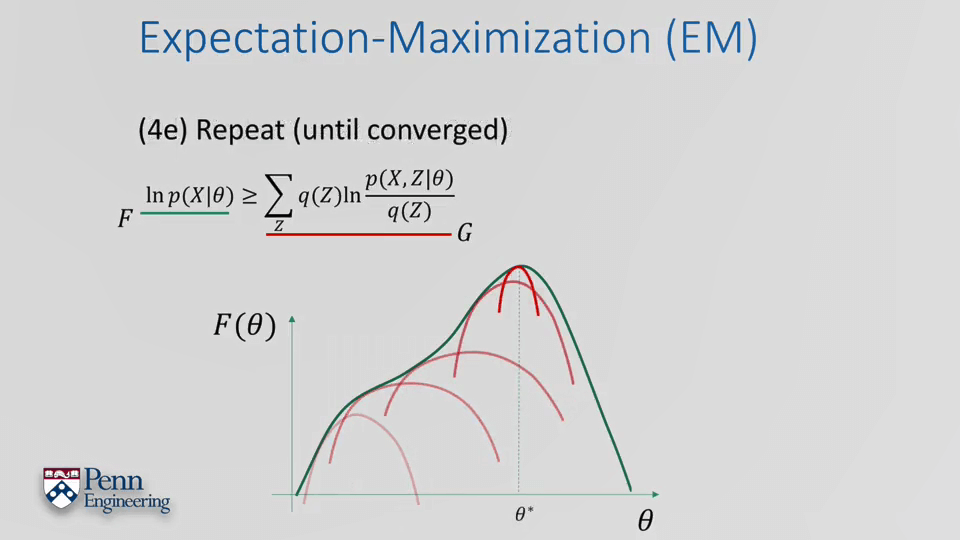 EM算法总的流程如下:
EM算法总的流程如下:


本文作者原创,未经许可不得转载,谢谢配合
