Robotics:Estimation and Learning课程Week1的测验与作业习题，如果有错误的地方欢迎提出、交流。注意本博客中的题目与答案仅供学习交流使用，严禁用于抄袭等不守信行为。若因抄袭答案导致Coursera账号被取消激活，本博客概不负责。文章中有几个GIF动图，所以加载速度可能会慢一些，可以稍微缓冲一下再阅读。
1.Tests
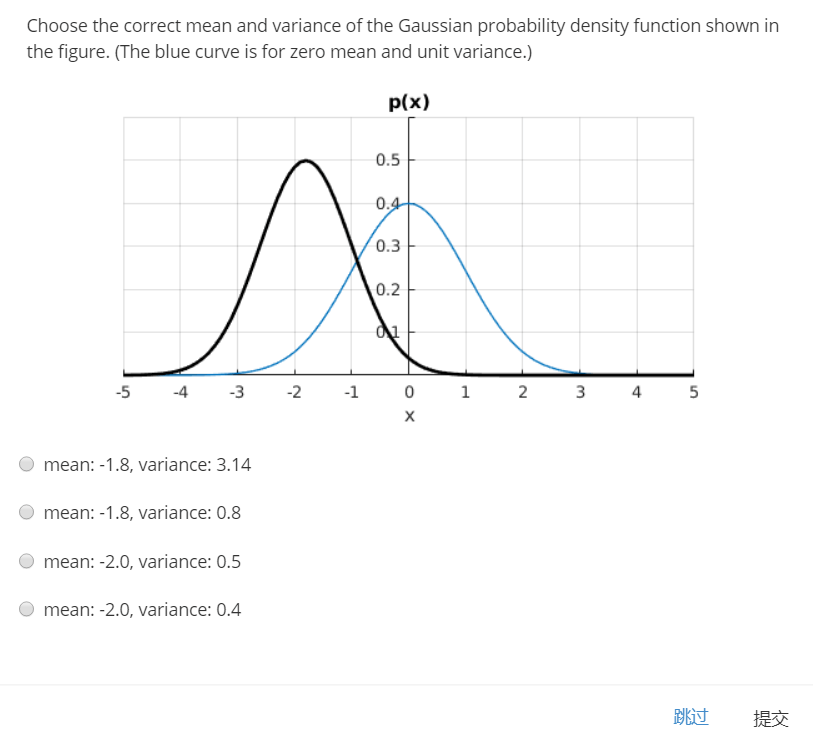考察均值与方差对高斯分布的影响。均值影响曲线位置，方差影响曲线胖瘦。图中蓝色曲线为标准正态分布，而黑色曲线要比它更瘦，也就意味着方差更小且小于1。同时黑色曲线的中心在-1.8，也就是说均值为-1.8，所以选B。
考察相关定义，选D。
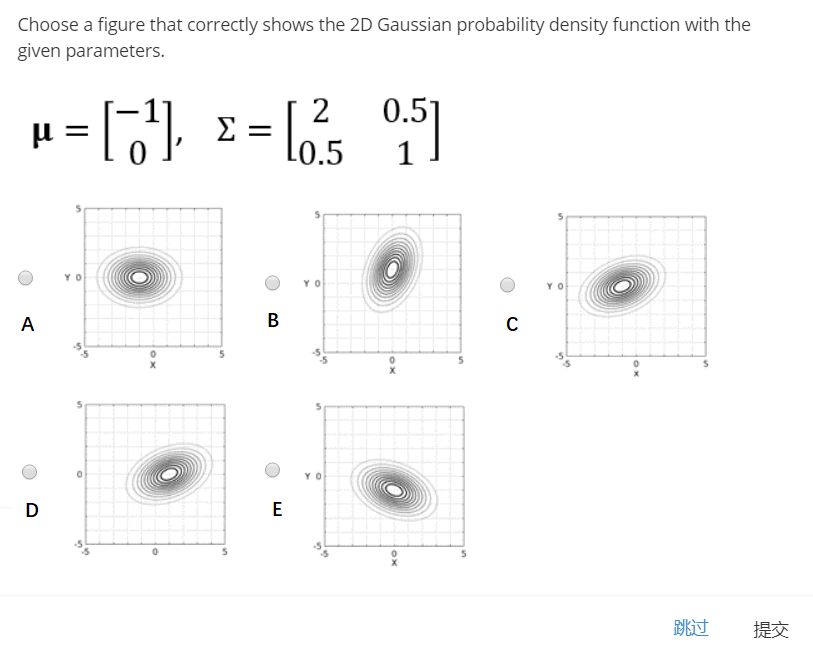与第一题类似，考察多变量高斯中各参数的影响。根据题目，x方向均值为-1，y方向为0，因此可以直接排除B、D、E。而由于x、y之间存在相关性，因此不再是关于坐标轴对称，因此选C。
考察对于高斯混合模型的描述。GMM不像单高斯模型一样，没有解析解。高斯模型的个数并非越多越好，而是要合理选择。如果不限制高斯模型数量，GMM可以表达任意的分布。因此答案选B。GMM可以看作是一系列高斯模型的加权和。
考察对于EM算法的描述。EM是一种迭代算法，正是因为不存在解析解才会需要迭代。EM中的隐变量无法直接观测。所以最终答案选A。EM算法需要迭代的初值。
2.Assignment
这次的作业其实前面一直有提到，就是利用高斯分布实现对于特定颜色小球的识别与定位，效果如下。
作业相关材料放在了百度云，链接：https://pan.baidu.com/s/1kYhulr0zdPAVNb4rNVZi1A 提取码：qros。
具体说来，需要我们修改的是detectBall.m文件，用于实现主体功能。而在此之前，我们需要自己确定使用的高斯模型，以及获得指定小球的颜色信息。因此我们需要基于example_rgb.m脚本结合自己选择的高斯模型进行修改。一些基本的操作已经帮我们写好了，比如选择目标区域的颜色等等，Matlab中都有现成的函数可以调用，如下所示。
结合前面所学知识，要对小球进行识别，可以有多种方法：如在HSV色彩空间中的Hue通道上利用1D高斯模型进行识别；也可以在RGB空间里选择R、G通道基于2D高斯模型进行识别；还可以基于GMM进行识别。在本次作业中，主要对三种方法都进行了实现。
(1)HSV空间中的1D高斯
思路其实很简单，读取图片以后转换到HSV空间，然后手动指定目标区域，获得了多个目标区域的Hue通道信息后就可以计算均值与方差，从而构建一个高斯分布，核心代码如下。完整代码及详细注释见SG_hsv.m。
% 1D Gaussian Model, Hue Channel
hsv_mu = mean(Samples); % 计算均值
% 计算方差
% 这里需要注意的是计算时一定要看清楚计算的维度，计算的是列方差还是行方差，结果不同
% 默认是按行计算方差，按列计算方差需要输入参数1
% 此外注意求的是σ表示的是标准差而不是方差，所以开根号，对应高斯公式中的σ平方
hsv_sig = sqrt(var(Samples,1));
save('SG_mu','hsv_mu');
save('SG_sig','hsv_sig');
hsv_mu,hsv_sig
save('SG_samples','Samples');
基于这些散点，计算其在Hue通道上的高斯分布如下图所示。
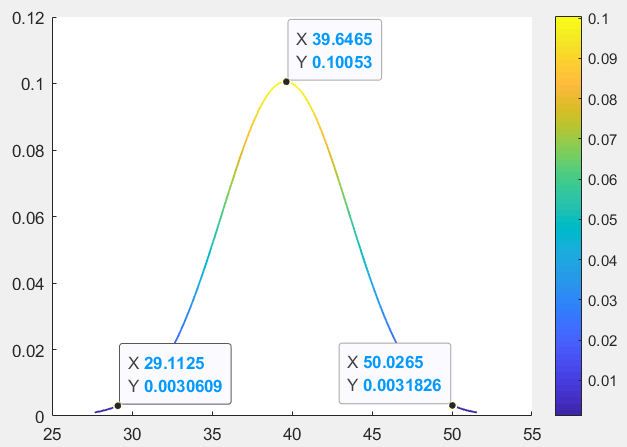基于这个分布，再设置概率阈值(例如作业中阈值为2σ)就可以对小球进行识别与区分了。部分检测代码如下。完整代码见detectBall.m的HSV部分。
% HSV(Hue) 1D Gaussian
mu = 39.5989;
sig = 3.9681;
% 阈值根据参数自动算出，取2σ的概率作为阈值
thre = exp(-power(2*sig,2)/(2*sig^2))/(sqrt(2*pi)*sig);
% HSV方法
img_hsv = rgb2hsv(I);
channel_h = img_hsv(:,:,1) * 256; % 前面求解参数的时候乘了256，这里保持统一，也乘以256
% 计算每个像素的概率
prob_img = exp(-power(channel_h-mu,2)/(2*sig^2))/(sqrt(2*pi)*sig);
prob_mask = prob_img>thre; % 阈值操作，初步确定掩膜
识别效果如下。
(2)RGB空间中的2D高斯
上面也说了，除了在HSV空间中的Hue通道上进行判断，也可以直接在RGB空间中进行判别。在判别时还需要注意的是选择几维的高斯，也即是选择两个变量还是三个变量。个人建议是选择2D高斯，因为相比于三个变量的高斯，2D高斯更加直观，且分布可以被可视化出来，而三变量高斯要想可视化得在四维空间。在选择2D高斯以后，另一个问题是选择哪两个变量，是Red Green、Red Blue还是Green Blue。为了更加准确地判断，在脚本中将三种情况都进行了可视化，可以根据可视化结果选择最好的组合。核心代码如下，完整代码见MG_rgb.m。
% Multivariate Gaussian Model, R G B
% 这里求解的是一个三个变量(R、G、B)的高斯分布，但在实际应用时可以只用2个变量的高斯分布
% 直接从求得的均值与方差中选取对应数据即可
% 之所以没有使用三变量高斯分布是因为不够直观，没办法画出分布图(四维空间)
% 两变量高斯分布可以在三维空间画出分布图
% 当然如果硬是要用也是完全可以的，输入变量为R、G、B即可，可能阈值的确定稍微麻烦些
rgb_mu = mean(Samples); % 计算各维度(列)的均值
samples_cen = double(Samples)-rgb_mu; % 对原始数据减去均值获得中心化后的数据
[number,dim]=size(samples_cen); % 获取数据个数
% 按照公式求解协方差矩阵
% 一定需要注意的是求解得到的是方差和协方差，也就是说其实并不是σ，而是σ平方
% 如果不开根号的话，那么再后面用协方差矩阵计算的时候就不用再平方了
rgb_sig = (1/number)*(transpose(samples_cen)*samples_cen);
save('MG_mu','rgb_mu')
save('MG_sig','rgb_sig')
rgb_mu,rgb_sig
save('MG_samples','Samples')
不同变量组合的可视化结果如下。
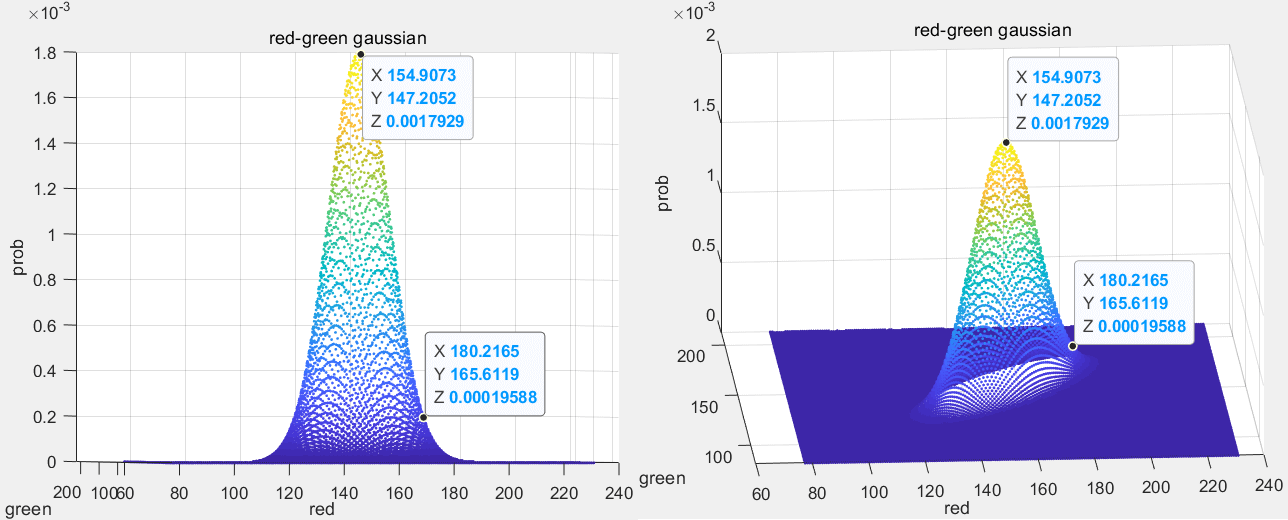Red和Green组合
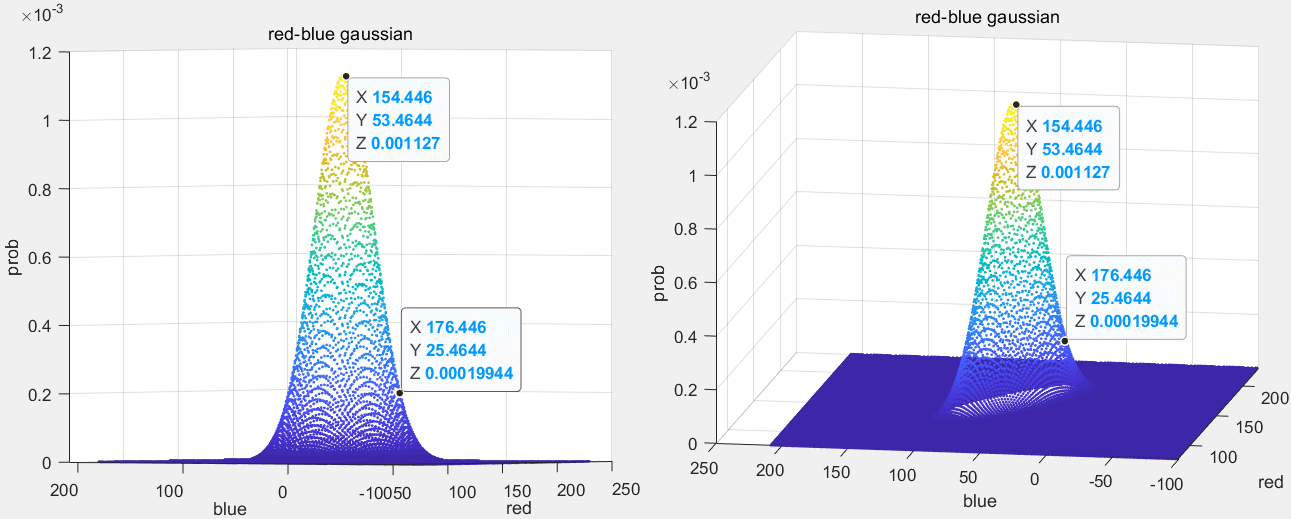Red和Blue组合
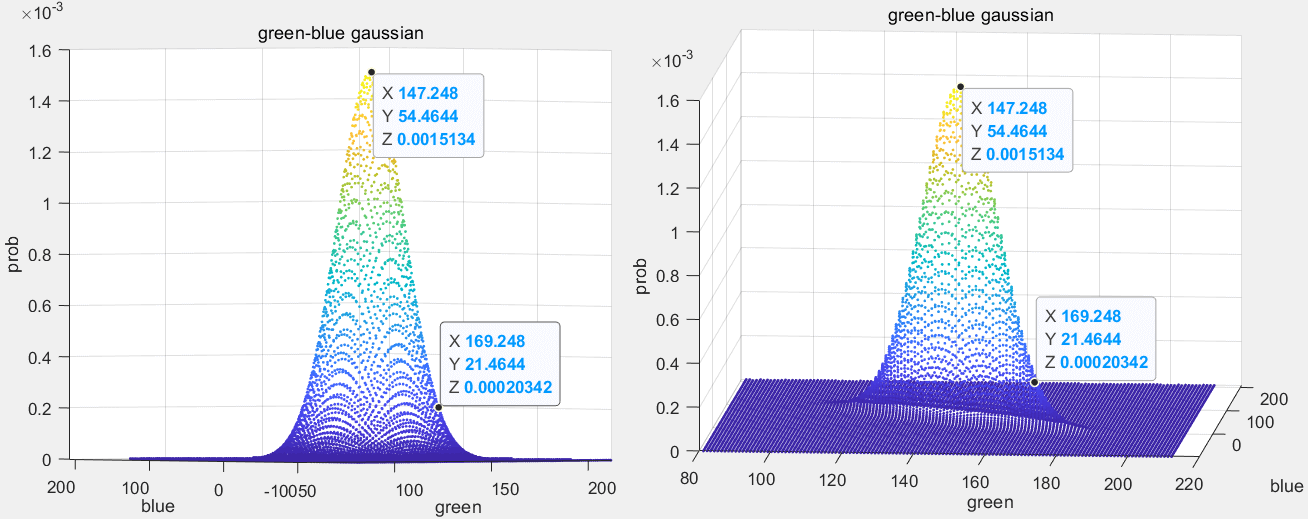Green和Blue组合
最终可以看出Red和Green搭配的高斯分布有最高的极值，因此选择它们作为变量。部分检测代码如下，完整代码见detectBall.m的RGB部分。
% RGB(Red Green) 2D Gaussian
mu = [154.1404 146.9795];
sig = [153.3888 111.0477;
111.0477 131.4629];
% 阈值根据数据分布图得出
% 当然也可以对数据进行去相关化以后自动计算
% 但有些复杂，因此这里没有采用这种办法
thre = 0.0002;
% Red and Green Channel 这里也可以试试其它两种组合，对应参数换一下即可
R_channel = double(I(:,:,1));
G_channel = double(I(:,:,2));
B_channel = double(I(:,:,3));
[height,width,t] = size(I); % t是临时变量，接收不需要的参数
[t,D] = size(mu);
prob_img = zeros(height,width);
for i=1:height
for j=1:width
tmp_val = [R_channel(i,j),G_channel(i,j)];
prob = exp(-0.5*(tmp_val-mu)*inv(sig)*(tmp_val-mu)')/(power(2*pi,D/2)*sqrt(det(sig)));
prob_img(i,j)=prob;
end
end
prob_mask = prob_img>thre;
基于它们最终识别的效果如下。
(3)GMM模型
高斯混合模型相较于前两个模型要更加复杂一些，一方面需要自己确定每个高斯模型的变量，另一方面还需要确定GMM中高斯模型的个数。确定好这些以后还需要确定迭代初值，并用EM算法迭代进行参数估计。完整代码见GMM_gh.m。
首先是高斯模型的变量选择，这里我选择了两个变量，分别是灰度以及HSV中的Hue。根据这两个变量构建一个2D高斯模型。同时整个GMM中包含3个2D高斯，各模型之间等权。
为了能够相对准确地确定初值，首先基于目标的灰度与色度(Hue)先计算出了一个2D高斯的参数，代码如下。
% 采用2D Gaussian先计算个分布，后面并没有使用，只是用来画了个图
calc_mu = mean(Samples); % 计算各维度(列)的均值
samples_cen = Samples - calc_mu; % 对原始数据减去均值获得中心化后的数据
[number,dim]=size(samples_cen); % 获取数据个数
% 按照公式求解协方差矩阵
% 一定需要注意的是求解得到的是方差和协方差，也就是说其实并不是σ，而是σ平方
% 如果不开根号的话，那么再后面用协方差矩阵计算的时候就不用再平方了
calc_sig = (1/number)*(transpose(samples_cen)*samples_cen);
以此作为参考，对三个2D高斯模型进行初值设置，如下。
% 这里需要注意的是，各高斯模型的初值不能相同
% 如果相同的话就是这个高斯分布，直接收敛了
% 也不能相差倍数，彼此之间成线性关系，这样的话收敛不了
% 因此，为了能正常收敛，三个高斯模型的参数分别设为：
mu1 = [128 30];
sig1 = [15 1;1 20];
mu2 = [137 35];
sig2 = [10 2;2 15];
mu3 = [135 40];
sig3 = [7 1.5;1.5 9];
init_mu = [mu1;mu2;mu3];
init_sig = [sig1;sig2;sig3];
初值设置好以后就开始利用EM算法进行迭代了。核心代码如下。
[len,t] = size(Samples);
past_mu = zeros(3,2);
past_sig = zeros(6,2);
mu_th = 0.000001;
sig_th = 0.000001;
for it=1:500
% 收敛判断
diff_mu = sum(sum(abs(init_mu - past_mu)));
diff_sig = sum(sum(abs(init_sig - past_sig)));
if diff_mu < mu_th && diff_sig < sig_th
fprintf('\n第%d次迭代\n上次迭代均值\n',it);
disp(past_mu);
fprintf('当前迭代均值\n');
disp(init_mu);
fprintf('差异 %f\n',diff_mu);
disp(abs(init_mu - past_mu));
fprintf('上次迭代方差\n');
disp(past_sig);
fprintf('当前迭代方差\n');
disp(init_sig);
fprintf('差异 %f\n',diff_sig);
disp(abs(init_sig - past_sig));
fprintf('\n迭代完成\n估计均值\n');
disp(init_mu);
fprintf('估计方差\n');
disp(init_sig);
fprintf('均值差异 %f 小于阈值%f\n方差差异 %f 小于阈值%f\n停止迭代\n',diff_mu,mu_th,diff_sig,sig_th);
break;
end
fprintf('\n第%d次迭代\n上次迭代均值\n',it);
disp(past_mu);
fprintf('当前迭代均值\n');
disp(init_mu);
fprintf('差异 %f\n',diff_mu);
disp(abs(init_mu - past_mu));
fprintf('上次迭代方差\n');
disp(past_sig);
fprintf('当前迭代方差\n');
disp(init_sig);
fprintf('差异 %f\n',diff_sig);
disp(abs(init_sig - past_sig));
past_mu = init_mu;
past_sig = init_sig;
% calculate z
z = [];
D = 2;
for i=1:len
tmp_value = double(Samples(i,:));
prob1 = exp(-0.5*(tmp_value-init_mu(1,:))*inv(init_sig(1:2,1:2))*(tmp_value-init_mu(1,:))')/(power(2*pi,D/2)*sqrt(det(init_sig(1:2,1:2))));
prob2 = exp(-0.5*(tmp_value-init_mu(2,:))*inv(init_sig(3:4,1:2))*(tmp_value-init_mu(2,:))')/(power(2*pi,D/2)*sqrt(det(init_sig(3:4,1:2))));
prob3 = exp(-0.5*(tmp_value-init_mu(3,:))*inv(init_sig(5:6,1:2))*(tmp_value-init_mu(3,:))')/(power(2*pi,D/2)*sqrt(det(init_sig(5:6,1:2))));
z1 = prob1 / (prob1 + prob2 + prob3);
z2 = prob2 / (prob1 + prob2 + prob3);
z3 = prob3 / (prob1 + prob2 + prob3);
z = [z; [z1,z2,z3]];
end
% update mu
weight_mat = [];
sum1 = 0;
sum2 = 0;
sum3 = 0;
for i=1:len
sum1 = sum1 + z(i,1)*Samples(i,:);
sum2 = sum2 + z(i,2)*Samples(i,:);
sum3 = sum3 + z(i,3)*Samples(i,:);
end
new_mu1 = 1/sum(z(:,1))*sum1;
new_mu2 = 1/sum(z(:,2))*sum2;
new_mu3 = 1/sum(z(:,3))*sum3;
init_mu = [new_mu1;new_mu2;new_mu3];
% update sigma
sum1 = 0;
sum2 = 0;
sum3 = 0;
for i =1:len
cen_item1 = Samples(i,:) - init_mu(1,:);
sum1 = sum1 + z(i,1)*transpose(cen_item1)*cen_item1;
cen_item2 = Samples(i,:) - init_mu(2,:);
sum2 = sum2 + z(i,2)*transpose(cen_item2)*cen_item2;
cen_item3 = Samples(i,:) - init_mu(3,:);
sum3 = sum3 + z(i,3)*transpose(cen_item3)*cen_item3;
end
new_sig1 = 1/sum(z(:,1))*sum1;
new_sig2 = 1/sum(z(:,2))*sum2;
new_sig3 = 1/sum(z(:,3))*sum3;
init_sig = [new_sig1;new_sig2;new_sig3];
end
如下所示，在迭代了74次以后收敛，迭代完成。
第74次迭代
上次迭代均值
132.5361 39.9362
148.5888 41.0415
135.6962 38.3861
当前迭代均值
132.5361 39.9362
148.5888 41.0415
135.6962 38.3861
差异 0.000000
1.0e-07 *
0.0435 0.0048
0.3743 0.0674
0.4558 0.0414
上次迭代方差
36.7413 -7.7797
-7.7797 38.3178
15.4693 -1.9628
-1.9628 2.3955
18.8932 2.1208
2.1208 2.3284
当前迭代方差
36.7413 -7.7797
-7.7797 38.3178
15.4693 -1.9628
-1.9628 2.3955
18.8932 2.1208
2.1208 2.3284
差异 0.000001
1.0e-06 *
0.0836 0.0176
0.0176 0.1289
0.1701 0.0407
0.0407 0.0025
0.2401 0.1019
0.1019 0.0054
迭代完成
估计均值
132.5361 39.9362
148.5888 41.0415
135.6962 38.3861
估计方差
36.7413 -7.7797
-7.7797 38.3178
15.4693 -1.9628
-1.9628 2.3955
18.8932 2.1208
2.1208 2.3284
均值差异 0.000000 小于阈值0.000001
方差差异 0.000001 小于阈值0.000001
停止迭代
最终迭代后的GMM可视化如下图所示。可以看到相比于单个高斯模型，GMM“轻松”做到了单个高斯模型做不到的事情——双峰。
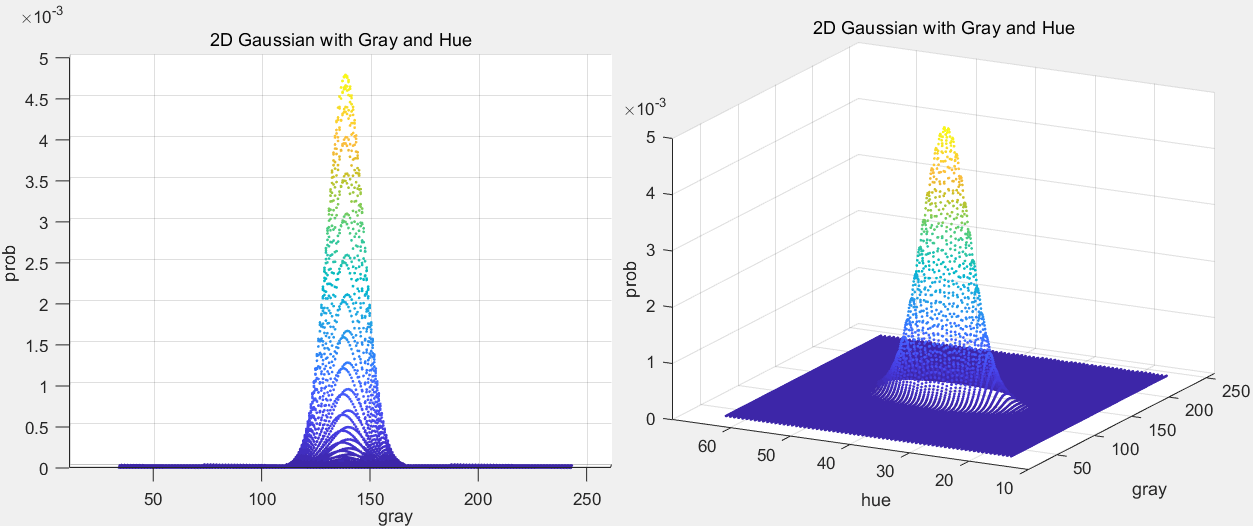
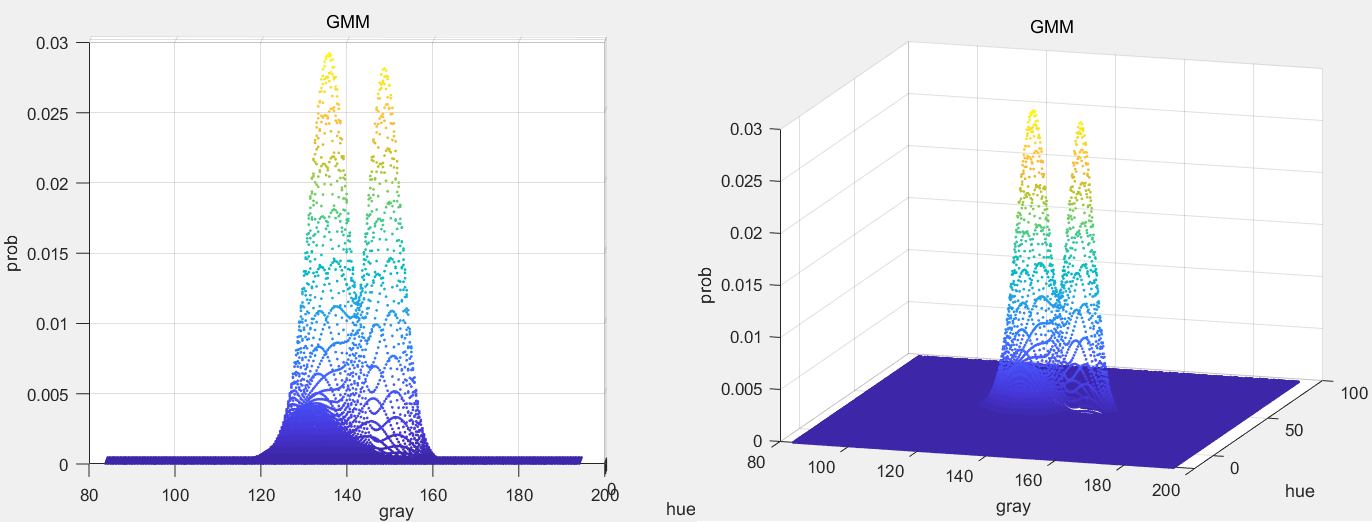单个2D高斯分布如下，可以和GMM进行对比。
采用GMM进行检测的部分代码如下，完整见detectBall.m的GMM部分。
% GMM(Gray Hue，3个2D Gaussian)
mu = [132.9384 39.8618;
148.6809 41.0354;
135.6902 38.3501];
sig = [38.2732 -8.3364;
-8.3364 39.9696;
15.4119 -1.9349;
-1.9349 2.3483;
18.9360 2.4449;
2.4449 2.3641];
thre = 0.003;
% GMM
R_channel = double(I(:,:,1));
G_channel = double(I(:,:,2));
B_channel = double(I(:,:,3));
gray = R_channel*0.299 + G_channel*0.587 + B_channel*0.114;
img_hsv = rgb2hsv(I); % 将RGB转换为HSV
channel_h = img_hsv(:,:,1)*256;
[t,D] = size(mu);
[height,width,t] = size(I);
for i=1:height
for j=1:width
val = [gray(i,j),channel_h(i,j)];
prob1 = exp(-0.5*(val-mu(1,:))*inv(sig(1:2,1:2))*(val-mu(1,:))')/(power(2*pi,D/2)*sqrt(det(sig(1:2,1:2))));
prob2 = exp(-0.5*(val-mu(2,:))*inv(sig(3:4,1:2))*(val-mu(2,:))')/(power(2*pi,D/2)*sqrt(det(sig(3:4,1:2))));
prob3 = exp(-0.5*(val-mu(3,:))*inv(sig(5:6,1:2))*(val-mu(3,:))')/(power(2*pi,D/2)*sqrt(det(sig(5:6,1:2))));
prob = prob1 + prob2 + prob3;
prob_img(i,j)=prob;
end
end
prob_mask = prob_img>thre;
检测效果如下。
可以看到相较于前两个模型，由于概率阈值设置的相对较高，因此检测的小球更加细碎一些。如果适当降低阈值会好一些。
最后，完整的作业代码上传到了百度云，链接：https://pan.baidu.com/s/1g-ElDcZyoFtEYXTPPiTsTQ 提取码：o3ox。
本文作者原创,未经许可不得转载,谢谢配合
