对某抽奖游戏中奖率随抽奖次数变化的数学探讨

• 1.背景
• 2.问题抽象与建模
• 3.问题求解
• 4.代码实现与模拟
• 5.结论与总结

1.背景

事情的起因是这样的，昨天晚上在某个课程群里有人发起了个填写问卷抽奖送书的活动。 也许那一刻欧皇附体，就让我抽中了。 开心之余对于消息里的“中奖概率一致不必着急！”产生了怀疑。因为很简单，一共只有10本书，如果在你抽之前10本书都被抽完了，那么即使你中奖也拿不到书了。中不中奖是通过游戏里的转盘控制的，所以可以认为中奖概率是不变的(从这个角度可以认为她说的是对的)，但问题在于书的数量是有限的。中奖且能拿到书这两件事件同时发生的概率显然是会随抽奖先后顺序变化的，不是一致的，与抽奖的先后有显著的关系。

因此自然而然地便有了这个问题：如果“中奖且能拿到书”这个事件随抽奖先后变化，那么什么时候它发生的概率最大(最容易中奖)呢？对于这个问题的解答也就是本篇博客的主要内容了。

2.问题抽象与建模

对于上面这个例子，我们可以进行如下抽象。抽象之前先进行一些变量定义和必要的假设。首先我们认为单就中不中奖这个事件而言，不同人之间是相互独立的(比如大家转的都是同样的转盘，转盘上中奖与不中奖的格子分布没有变化)。进而我们假设每个人抽一次中奖的概率是\(P_{prize}\)，抽奖方一共设置了\(m\)个奖品。现在需要求第\(i\)个人抽奖，中奖且能拿到奖品的概率\(P_{i}\)。

3.问题求解

对于第\(i\)个人中奖且能拿到奖品的概率\(P_{i}\)的表达式，我们可以采用归纳推理的方式找到。“中奖且能拿到奖品”其实是“中奖”和“能拿到奖品”这两个事件的联合概率。而前面也提到了，每个人中奖的概率不变，都是\(P_{prize}\)，因此我们只需要求“能拿到奖品的概率”即可。对于这个概率可能不太好求，我们可以求它的逆事件：拿不到奖品的概率。对于第\(i\)个人而言，在什么情况下拿不到奖品呢？那就是前面\(i-1\)个人已经把所有奖品都抽完了。因此我们可以写出下式：

前面一共有\(i-1\)个人，抽完奖品也就是说有\(m\)个人拿到了奖品。一共有多少种情况呢？这是个典型的排列组合问题，用它就可以很容易得到所有可能的情况。另外需要注意一下的是对于排列组合，如果\(i-1\)小于\(m\)，它的结果为0。而每个人中奖概率是\(P_{prize}\)，\(m\)个人同时中奖的概率就是\(P_{prize}^{m}\)。将\(P_{prize}^{m}\)和\(C_{i-1}^{m}\)相乘，得到的就是\(m\)个人同时中奖这个事件一共可能发生的概率。再用1减去它，得到的就是“能拿到奖品的概率”：

最后，别忘了我们求解的是“中奖”与“能拿到奖品”的联合概率，再把对应概率相乘即可：

4.代码实现与模拟

有了上面的式子，我们就可以很容易求得不同次序时中奖且能拿到奖品的概率了。用Python简单实现如下：

from scipy.special import comb
from matplotlib import pyplot as plt


def calc_prob(prize_prob, prize_num, order_num):
    prob = prize_prob * (1 - pow(prize_prob, prize_num) * comb(order_num - 1, prize_num))
    # 计算出来的概率可能有一些异常情况，捕捉一下
    if prob < 0:
        prob = 0.0
    elif prob > 1:
        prob = 1.0
    return prob


if __name__ == '__main__':
    prize_prob = 1 / 10  # 中奖概率
    prize_num = 10  # 设置的奖品个数
    person_num = 100  # 抽奖的顺序

    index = []
    probs = []
    for i in range(1, person_num + 1):
        prob = calc_prob(prize_prob, prize_num, i)
        print(i, prob)
        index.append(i)
        probs.append(prob)

    plt.plot(index, probs)
    plt.grid()
    plt.show()

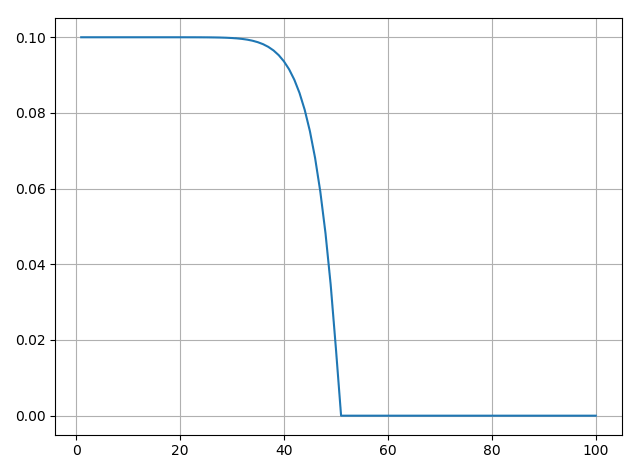
运行后结果如下。 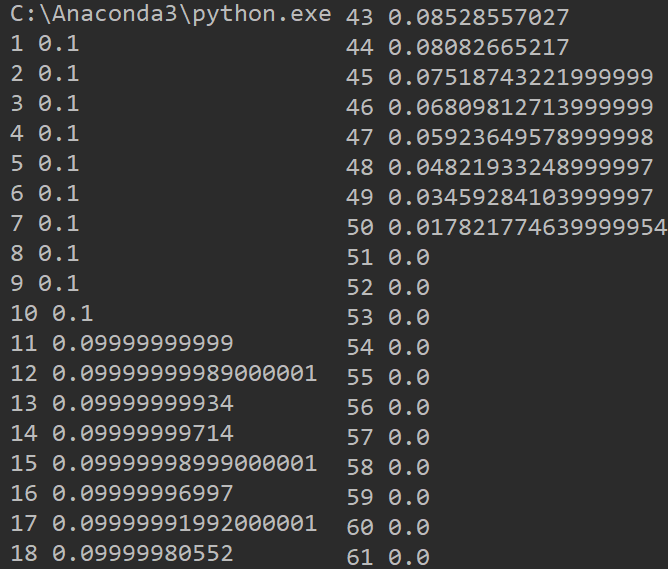从图中可以很明显的看到“中奖且能拿到奖品”的概率是随着抽奖次序的增加而不断减少的。而从上面输出的概率中也可以看到，在前10个人抽的时候，中奖概率都是0.1。原因也很简单，因为总共抽奖的人数还没有奖品个数多，怎么也不会出现奖品被抽完的情况，这个事件发生的概率为0，对应上面公式中1后面的那部分为0，就是单次中奖概率乘1。这也对应上面提到的排列组合中底数小于指数的情况，如\(C_{2}^{4}=0\)。在10次以后，概率会逐渐减小，直到最后所有奖品被抽完，后面的人再也拿不到，概率为0。

5.结论与总结

利用上面的代码你当然可以试试不同参数对结果的影响，如改变中奖概率对结果影响等。这个是很容易想到的，中奖概率越高，曲线下降的越快，如下是中奖概率为0.5时的曲线。 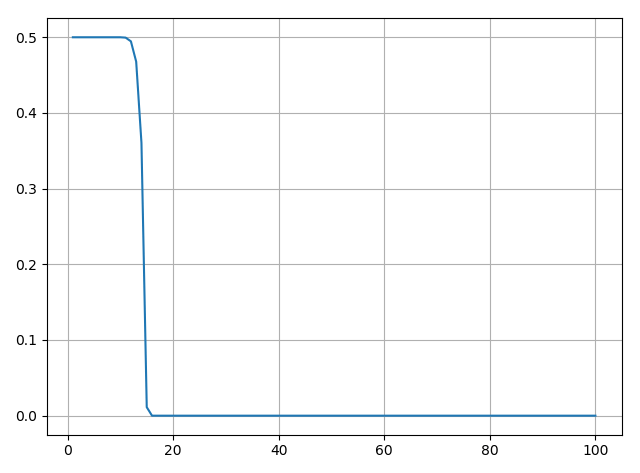回答最一开始提出的问题，最后可以得出的结论是：在不超过奖品数量的次数内抽奖是最容易中奖且拿到奖品的。越晚抽，中奖且拿到奖品的概率越小，直至为0。或者说得更直白些就是对于奖品数量有限的抽奖游戏越早抽越好，这其实也是符合我们的常识的——奖品都被别人先抽走了，我还抽什么。这是对抽奖者的有价值的结论。

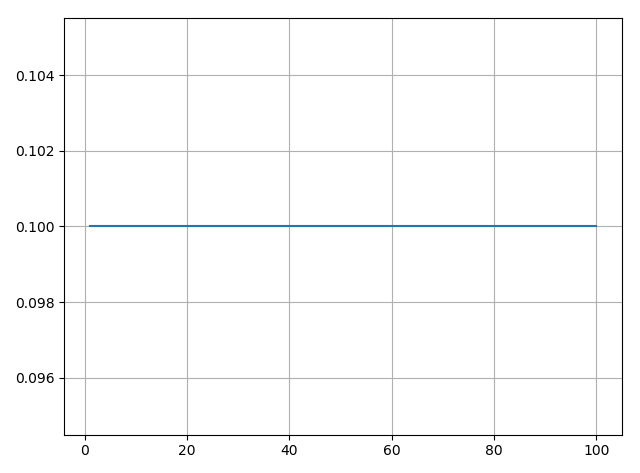
而对于举办方而言，要想真正保证“中奖且能拿到奖品”的公平，而不是表面上的“中奖”的公平，同样需要根据上面的式子设置一个合适的中奖率和奖品个数。如在不增加奖品个数的情况下降低中奖率、或不改变中奖率情况下增加奖品个数等等。例如在不改变中奖率的情况下，将奖品增加到45个，就可以保证公平，不受抽奖顺序的影响，如下图所示。