Matlab Tech Talk on Kalman Filter笔记

• 0.Introduction
• 1.Why Kalman Filter
• 2.State Observers
• 3.Optimal State Estimator
• 4.Optimal State Estimator Algorithm
• 5.Nonlinear State Estimators
• 6.Reference

0.Introduction

本篇博客对应Matlab在Youtube上的一个简短的Kalman Filter课程(Tech Talk)《Understanding Kalman Filters》，因为觉得介绍的还不错和通俗易懂，举例也比较简单。所以简单做些笔记。教程共包含7个小视频，都很短，总时长不超过一个小时，点击查看。 第一讲是背景和相关介绍，最核心的是2到5讲，而6到7讲则是利用Matlab的Simulink进行仿真模拟。下面话不多说就开始了。

1.Why Kalman Filter

第一讲视频点击查看。首先，视频里说什么是Kalman Filter？ 他给出一个例子说是一个咖啡过滤器。所以忍不住吐槽一下，可能也就只有你们西方人看到这个词会想到它吧喂，不是他说的话完全想不到这个层面。嗯，文化差异还是挺大的。然后他给出了一个比较一般的描述：

A Kalman filter is an optimal estimation algorithm.

也就是说卡尔曼滤波器是一个最优状态估计算法。然后，Kalman Filter有两个重要的用途并且分别举了两个例子。

首先，第一个用途是：(最优)估计无法直接测量的系统状态。这里他举了一个比较好玩但是又很实际的例子。 这个例子就是测量火箭发动机的温度。理想情况下，我们直接把传感器放到发动机上就可以直接测量。但现实往往是残酷的，比想象要更为复杂。因为发动机温度太高，传感器会融化，无法直接测量。因此一个比较可行的办法是测量发动机外侧的温度，然后根据这个外侧温度“最优地”估计无法直接测量的内部温度。利用Kalman Filter可以做到这一点，这便是Kalman Filter的第一个用途。

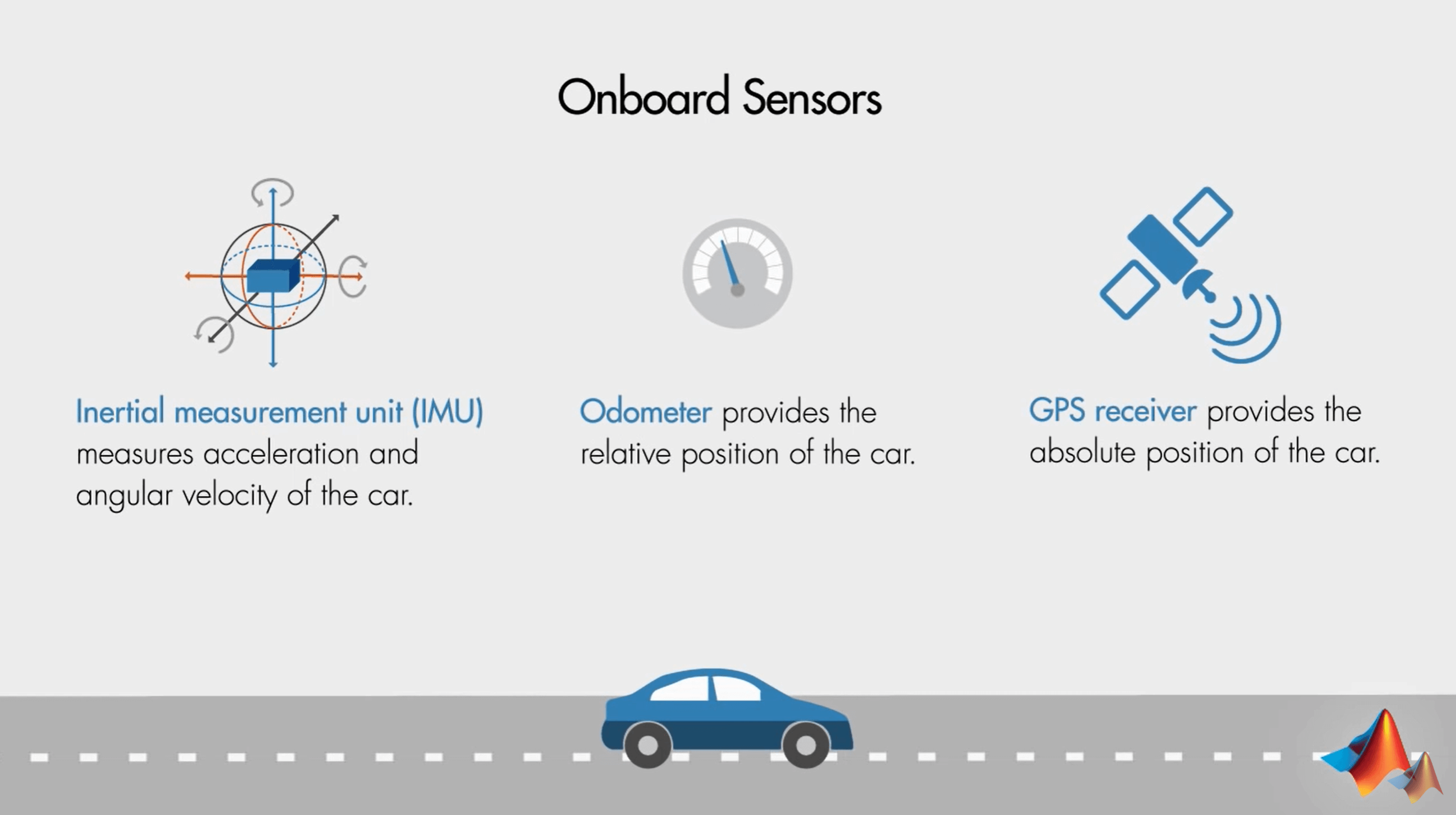
第二个用途是：带噪声的多源数据(传感器)融合。这里他也举了一个很实际的例子。 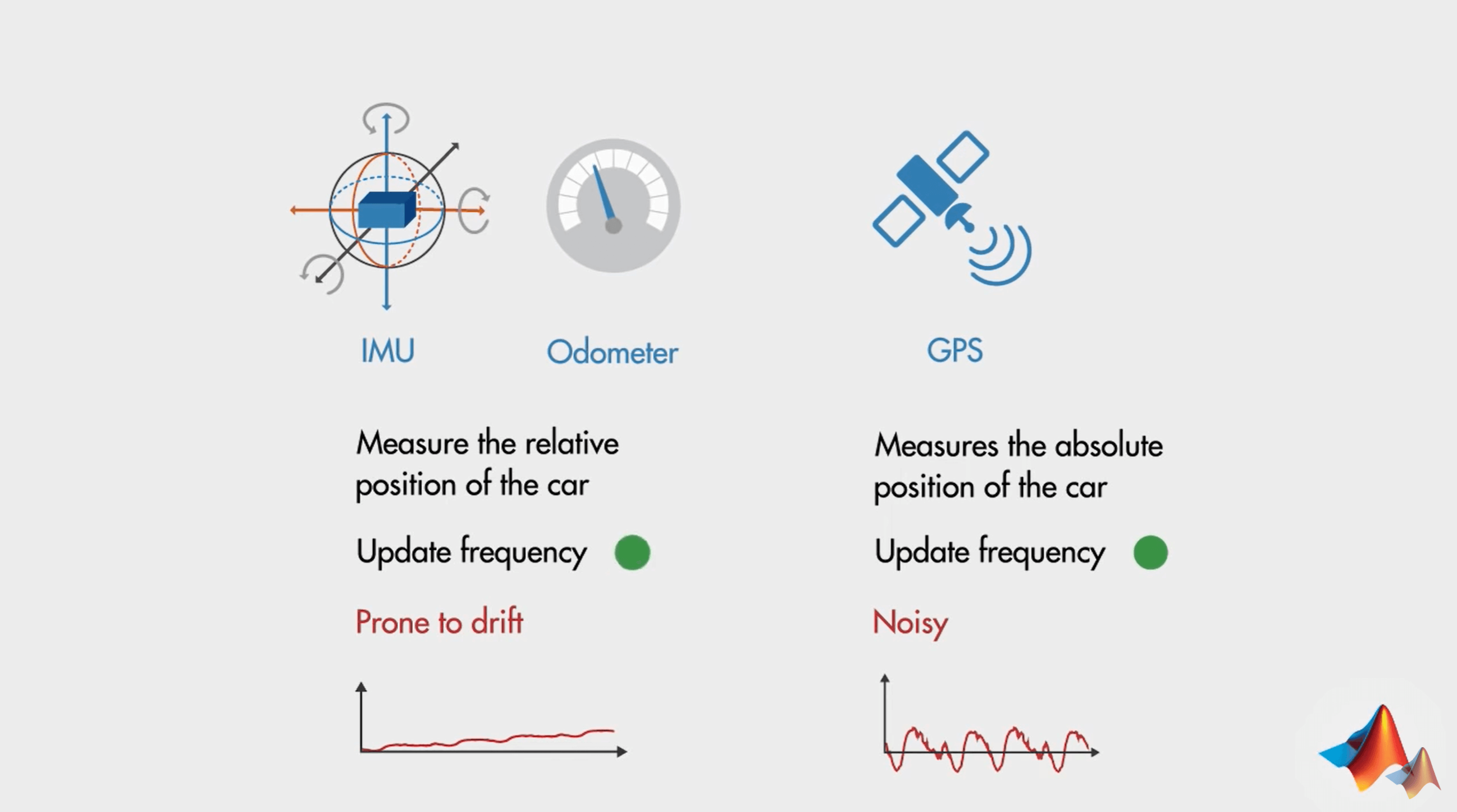你开着一个小汽车，要经过一个很长的隧道，但显然的，隧道里的信号很差，因此GPS测量的信号会不准，这时候可以依靠IMU和轮速计来辅助定位。但由于各个传感器测量的可靠性和噪声不同，直接融合可能无法获得最优结果。因此需要找到一个合适的多源数据(多传感器)融合手段。而这就是Kalman Filter的另一个重要作用了。通过Kalman Filter就可以实现在多个有噪声观测条件下，对感兴趣参数(状态)的最优估计，如速度、位姿等。

视频最后，介绍了一些和Kalman Filter有关的事实以及进行了总结。

2.State Observers

第二讲视频在这里，点击查看。在视频一开始，通过一个小例子介绍了什么是state observer。 简单来说，如上图，我们想要知道Timmy的心情怎么样，但我们没法直接观测。但我们可以给他一个饼干，然后看他的反应，根据他的反应就可以判断或者估计他的心情。另外，在之后出现的所有变量中，带有帽子符号的，都表示由state observer得到的估计状态(estimated state)。

还是第一讲提到的火箭的例子，如下图所示。我们期望得到火箭发动机内部的温度\(T_{in}\)，但是它无法直接测量，我们可以测量得到的是外部温度\(T_{ext}\)。 显然，外部温度\(T_{ext}\)和内部温度\(T_{in}\)是和输入的燃料量\(w_{fuel}\)有关系的。我们可以对这种关系进行初步的数学建模。这样当给定一个燃料输入的时候，我们就可以得到一个由模型估计的\(\hat T _{ext}\)和\(\hat T _{in}\)。当然，由于种种因素它估计的准不准就另说了。但是为了使我们估计的尽可能准一些(误差小一些)，所以我们需要找一个指标来评价误差。在这里，虽然\(\hat T _{in}\)可以得到，但是真值未知，因此不合适。适合做误差的就是我们估计的外部温度和测量得到的外部温度，我们认为，当它们之间的差异很小的时候，模型就可以比较逼近真实情况了，那么这个时候估计出来的内部温度也就是准的了。上面提到的这个模型，其实就是一个反馈控制系统(Feedback Control System)，如下图右边所示。我们希望控制的就是观测值和估计值之间的差异。 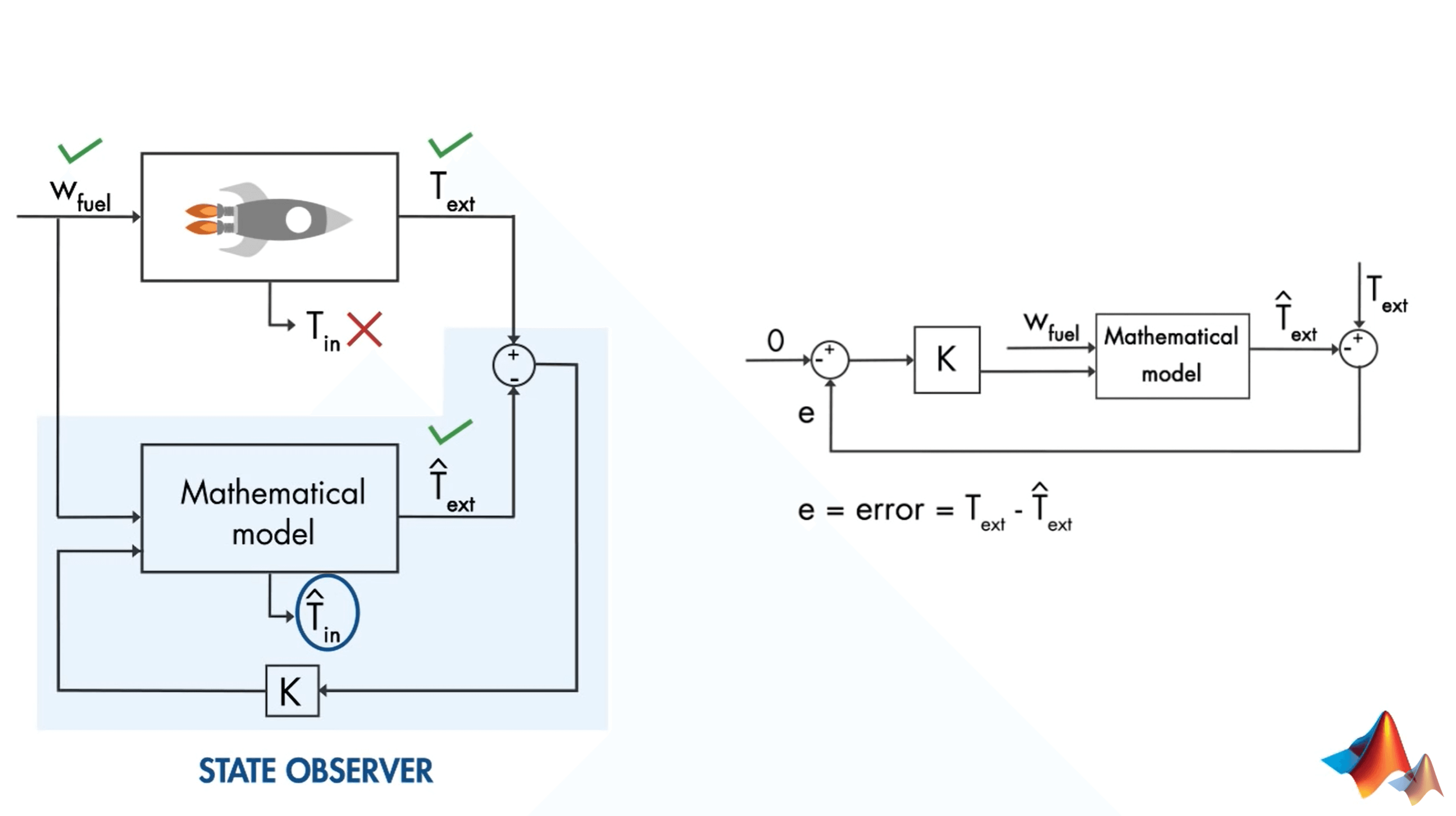当给定燃料量\(w_{fuel}\)时，我们可以根据数学模型得到估计的外部温度\(\hat{T}_{ext}\)，同时也可以测量得到真实的外部温度\(T_{ext}\)。然后通过控制器增益K进一步控制模型，最小化测量和估算的外部温度之间的差异。而如何选择最优的控制器K，会在下一讲讨论。下面是对刚刚说的模型的数学抽象表达。 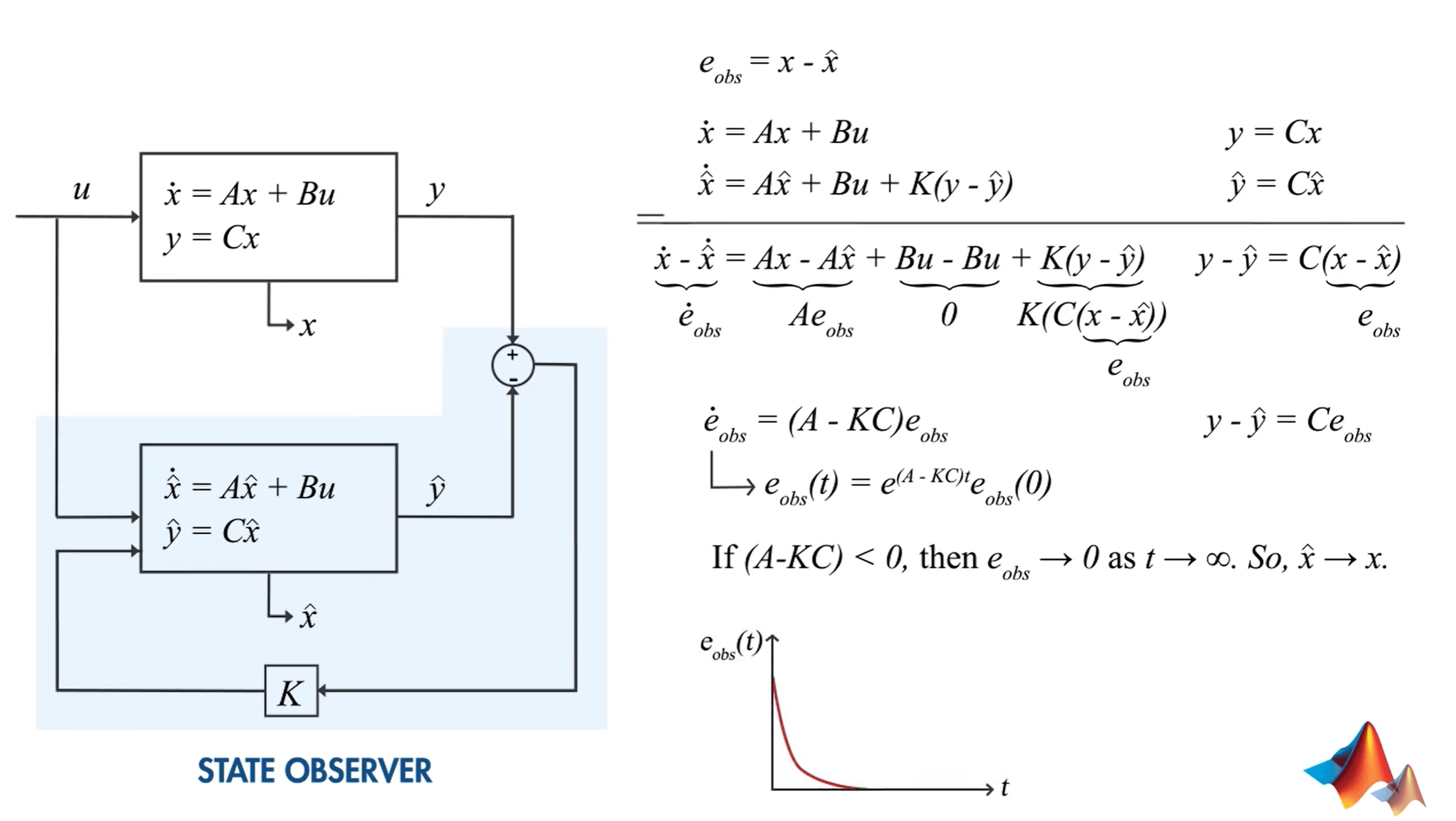这里，输入变成了\(u\)，输出和其估值变为\(y\)、\(\hat{y}\)，我们感兴趣的状态和其估计值分别为\(x\)、\(\hat{x}\)。这里，我们当然是希望感兴趣的估值误差最小，所以，可以定义误差\(e_{obs}\)为\(x-\hat{x}\)。我们把系统和观测的式子写出来，如右边所示。将其分别带入误差中，通过代数运算，就可以得到\(\dot{e}=(A-KC)e_{obs}\)。这个式子的解是一个关于时间t的对数函数。注意这里的变量，就是时间t。如果\(A-KC\)小于0，那么这个函数就是一个单调递减函数，如上面画的曲线所示，t越大，则\(e_{obs}\)越趋近于0。也就是说，误差越小，我们对状态\(x\)的估计越精确。当然你可能会发现，A本身也有可能小于0，这样没有K也可以收敛。 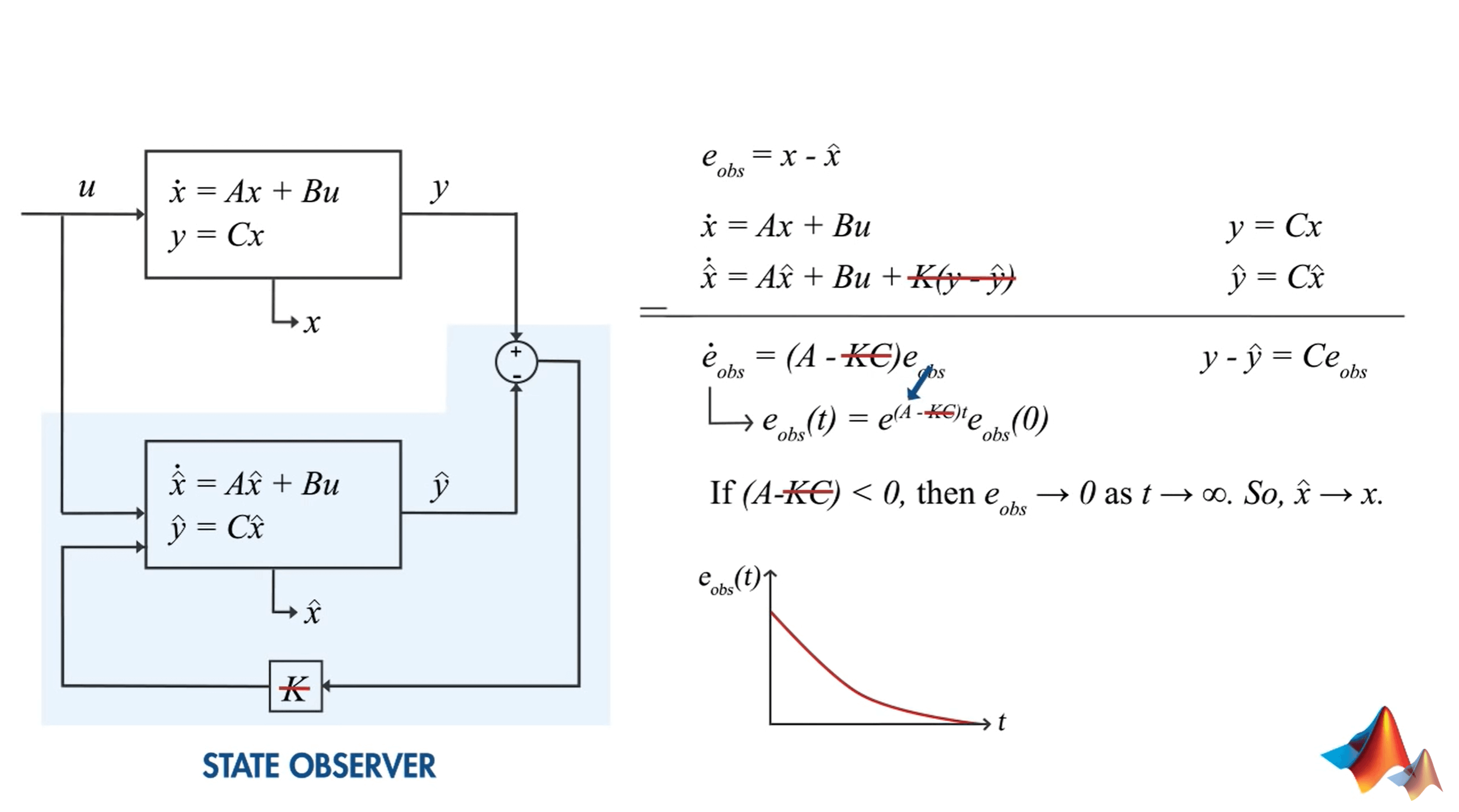这里K的意义在于我们可以通过选择相应的控制器增益K来控制误差函数的衰减率，比如可以加速收敛。如上图所示，函数的曲线明显要变得更平缓了。但如果没有K，我们就无法控制误差衰减的速度。使用反馈控制器可以更好地控制这些方程，并确保更快地消除误差。而选择增益K的最佳方法，也就是使用Kalman Filter。

3.Optimal State Estimator

第三讲的视频在这里，点击查看。视频开头，又举了一个我们不太常见但相对好理解的例子。 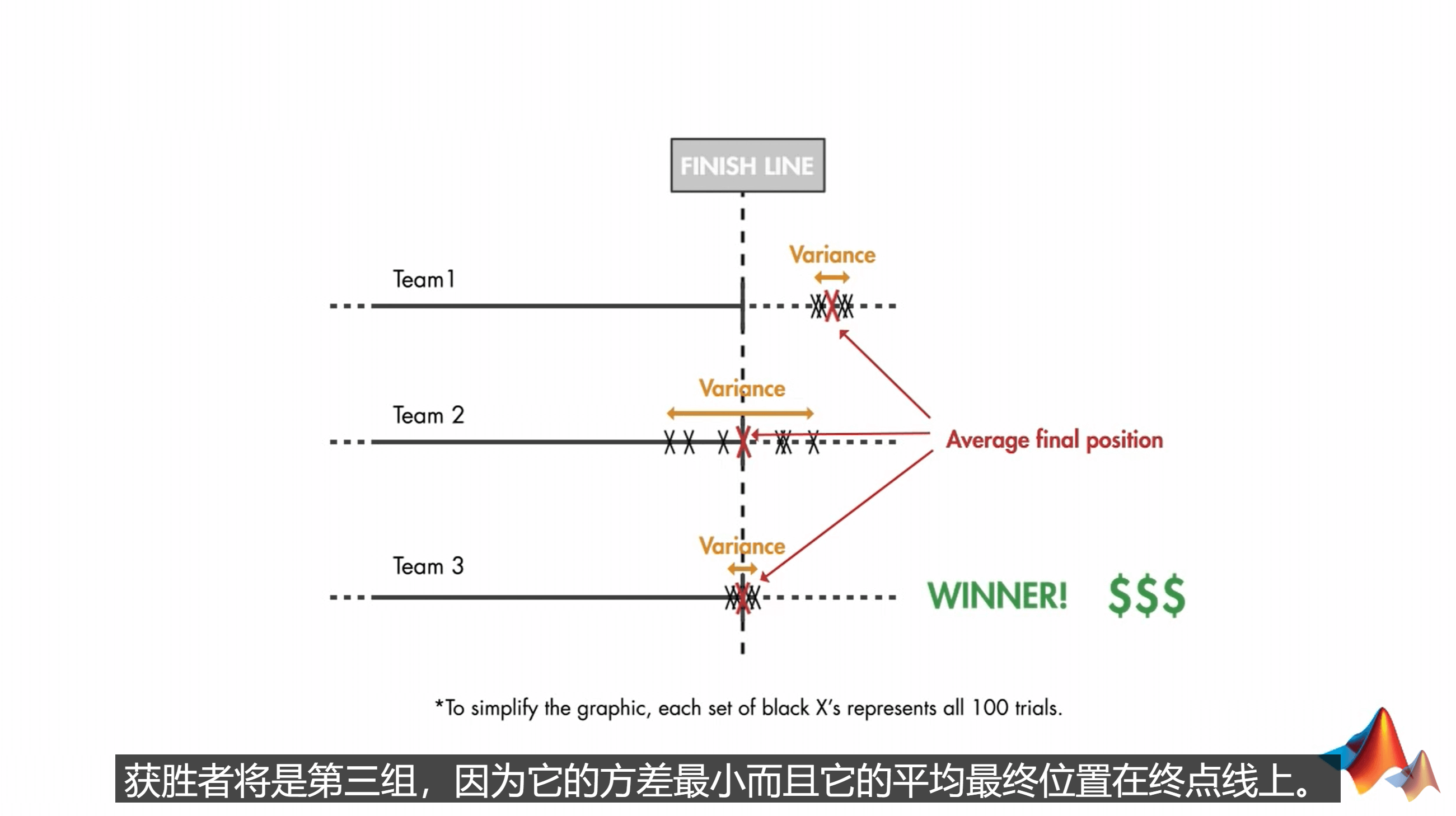也就是说，我有一辆车，要在100种不同的地形上跑1km。最后会统计这100次的均值和方差。均值最靠近1km，且方差最小即获胜。由于GPS有误差，所以我们要想获得最精确的位置不能够只依靠GPS，而是要参考其它测量数据，如IMU等。因此，我们可以用Kalman Filter来估算汽车的位置，从而判断我们是不是走了1km。 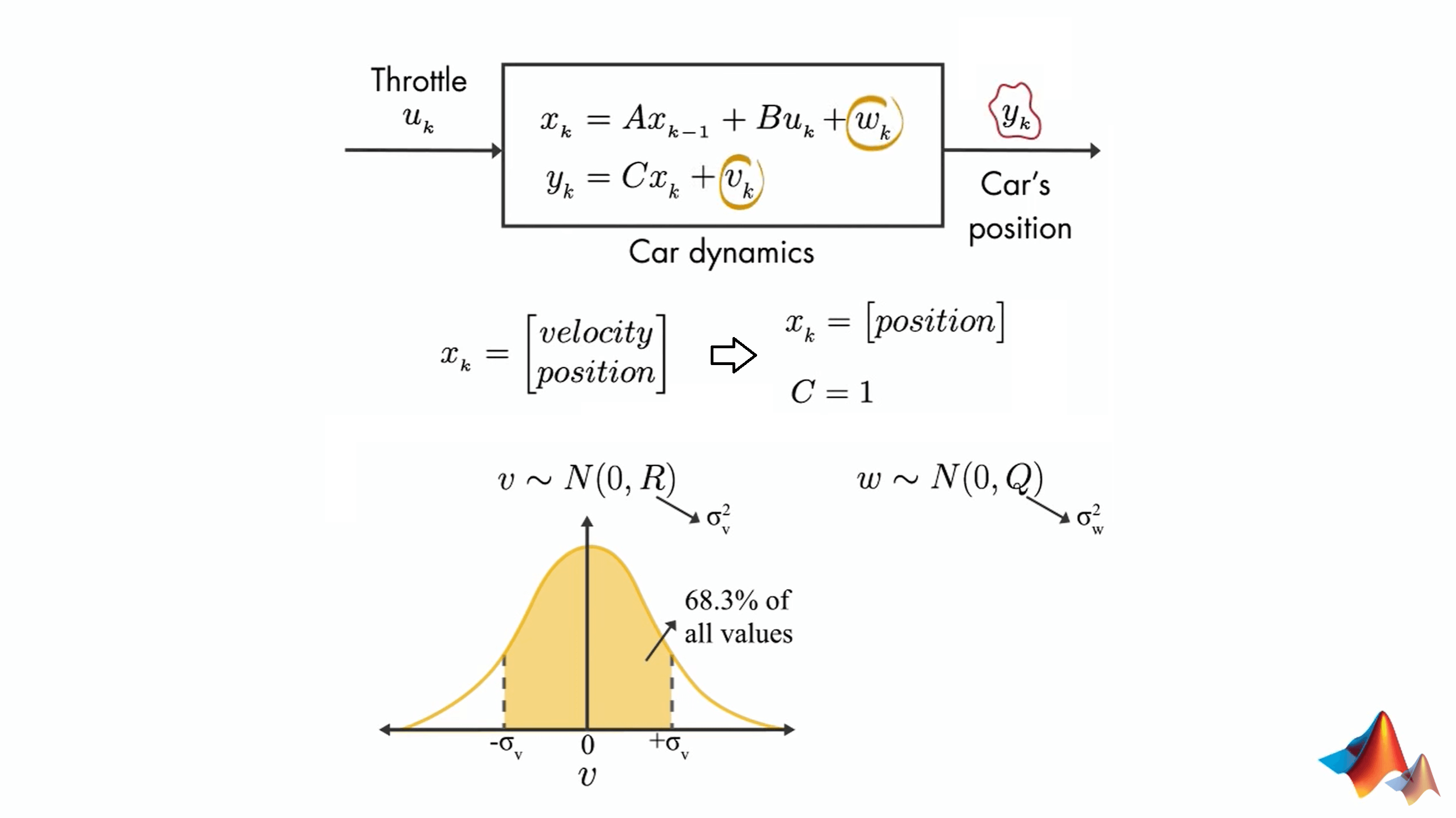对这个问题进行抽象，可以如上图所示进行建模。方框中第一个式子表示的是我们感兴趣的状态之间的关系，也即上一个状态与当前状态之间的关系。这种关系主要受三个因素影响，一是上一个状态，这很好理解，二是当前的控制，也很好理解，以及最后一个噪声因素。这三个因素共同决定了当前状态。而第二个式子表示的是我们感兴趣的状态和测量状态之间的关系。前面说了，我们感兴趣的状态\(x_{k}\)无法直接测量，但它和我们可以直接测量的\(y_{k}\)之间存在某种关系。这种关系就是用这个式子表示。同样的，这里依然会有噪声的影响。这里的两个噪声\(v\)、\(w\)都服从0均值的正太分布。另外需要说明的是，对于汽车而言，它在某一时刻可以包含多个状态，如速度、位置等。这里为了简化和叙述，我们只研究位置这一个状态。而我们的观测\(y_{k}\)也是位置，所以这里\(C=1\)。 同时，我们可以根据先验知识得到一个预测模型，从而可以估计得到\(x_{k}\)的估值。卡尔曼滤波就可以融合我们的观测\(y_{k}\)以及我们估计的\(\hat{x}_{k}\)，从而得到一个对于汽车位置最优的估计。这里第一个式子描述的是系统内部状态之间的变化关系，可以叫做状态转移方程。第二个式子描述的是感兴趣状态与我们可以直接观测到的状态之间的关系，可以叫做观测方程。下面的例子可以更有助于理解。 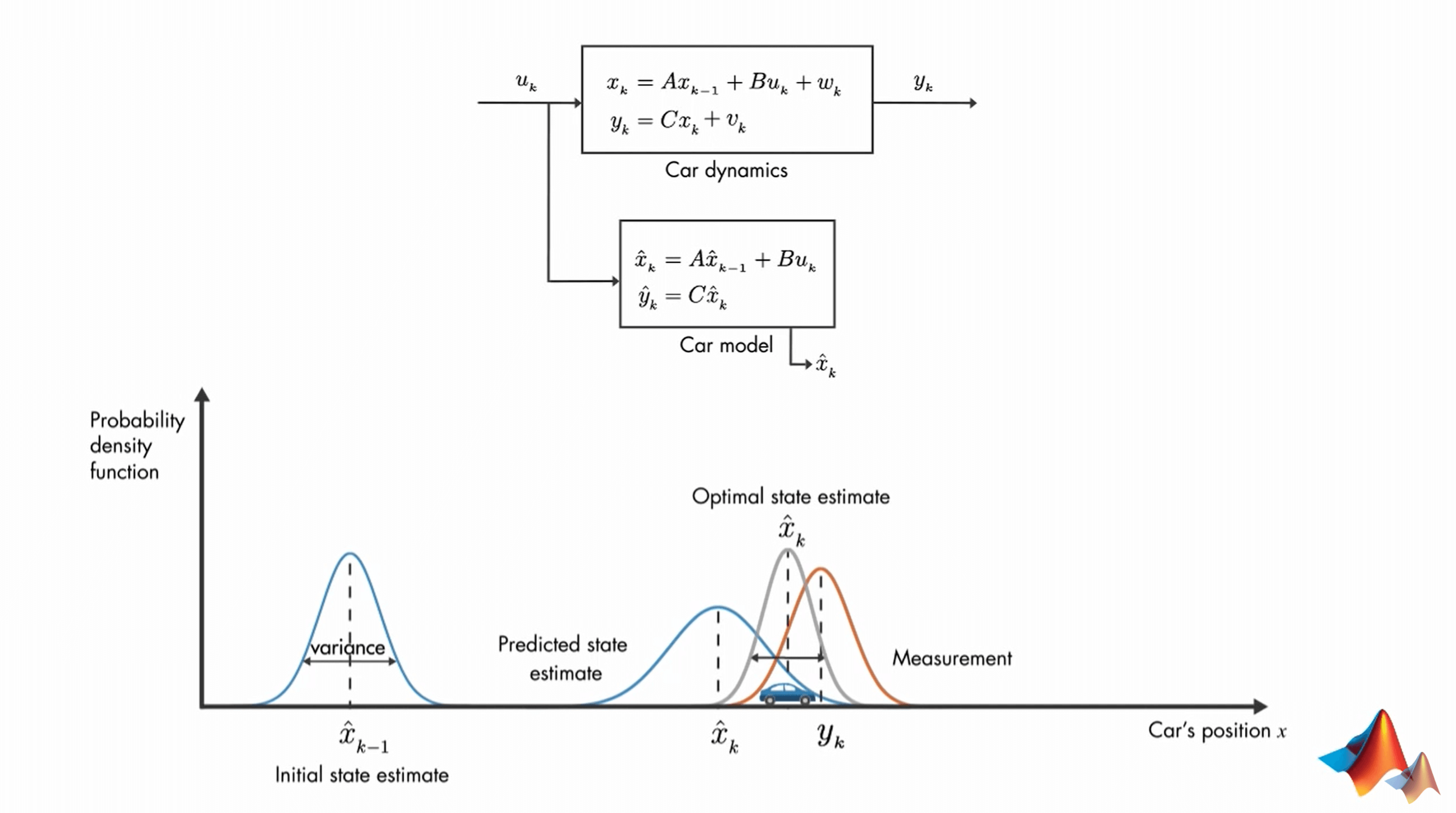如图所示，在\(k-1\)时刻，我们对系统的状态\(x\)(比如这里是汽车的位置)有一个估计值\(\hat{x}_{k-1}\)。根据建立的模型(比如这里是Car Model)，我们可以估计出\(k\)时刻系统的状态(汽车的位置)\(\hat{x}_{k}\)。但显然，这肯定会有误差的。同时，在\(k\)时刻，我们可以观测到系统另一个与状态\(x\)相关的量\(y_{k}\)。所以，\(k\)时刻汽车的位置到底应该在哪呢？估计值和直接测量值都存在误差，因此自然地，我们会想，那我们就把我们估计的状态\(\hat{x}_{k}\)和观测的状态\(y_{k}\)进行融合，就可以得到对于状态的最优估计了。更具体说就是，讲估计和测量的概率函数相乘，得到新的概率密度函数(根据高斯分布的性质可以知道，结果还是一个高斯分布)。这个高斯分布的均值，就认为是对于位置的最优估计。这便是Kalman Filter的核心思想。更进一步总结就是：将我们对状态\(x\)的预测与对状态\(y\)(与\(x\)存在某种关系)的观测进行融合，从而得到对于状态\(x\)的最优无偏估计。而关于如何进行具体的计算，见下一讲视频。

4.Optimal State Estimator Algorithm

第四讲的视频在这里，点击查看。这一讲继续上一个视频中最后举的例子，更具体地说明如何实现Kalman Filter。根据我们在第二讲里提到过的State Observer，可以发现Kalman Filter长的差不多。事实上，Kalman Filter就是一种State Observer，但是是针对随机系统而设计的。 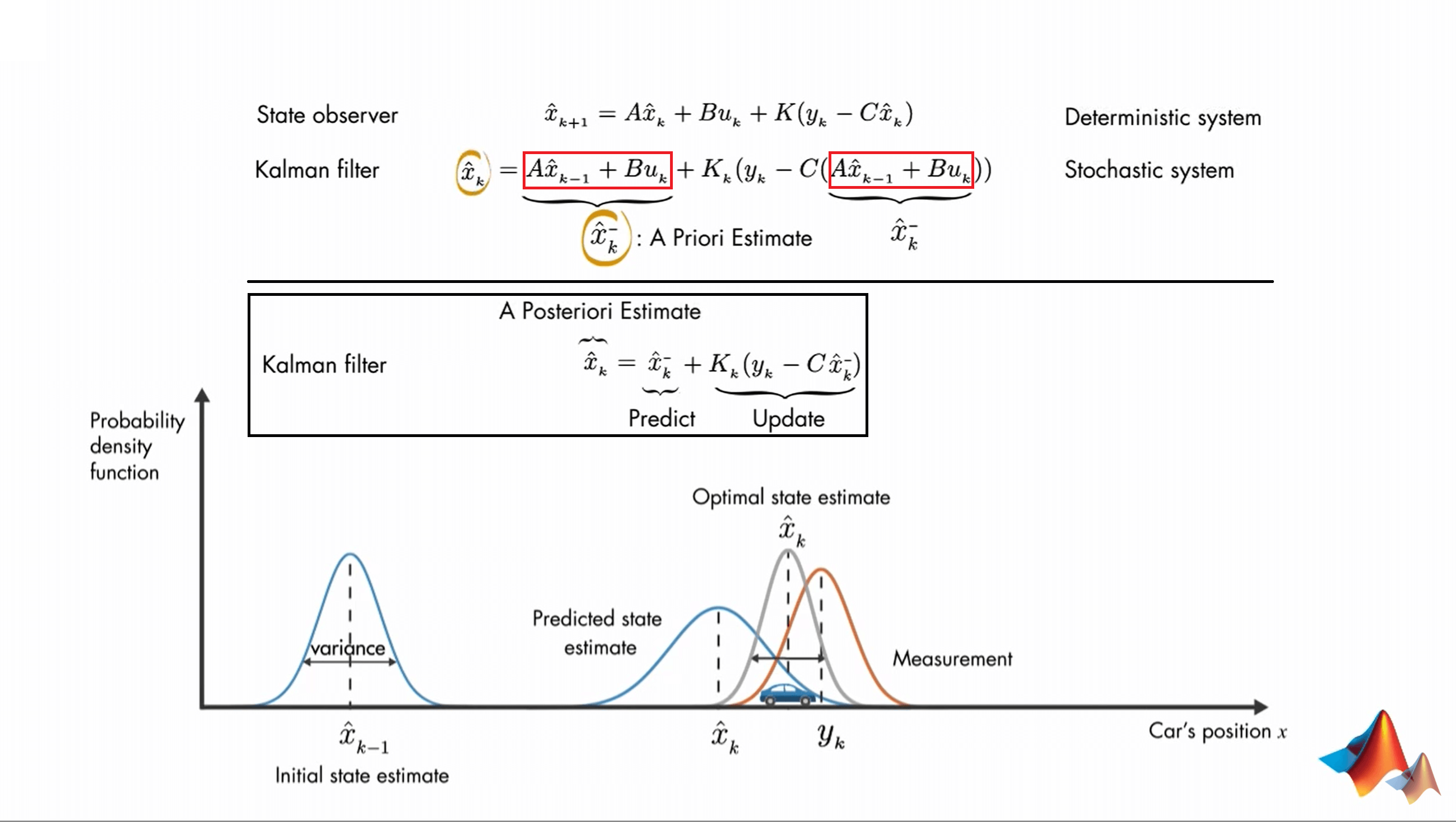这里，首先会根据上一个时刻\(k-1\)的状态\(\hat{x}_{k-1}\)以及当前时刻\(k\)的输入\(u_{k}\)，结合模型估计出一个初步的当前状态，为了避免混淆，这里用\(\hat{x}^{-}_{k}\)表示，叫做先验估计(Priori Estimate)。注意这里估计得到的状态并非最终的状态，而是在测量之前发生的，所以加了一个减号表示。说人话就是，在\(k\)时刻，我可以根据上一时刻\(k-1\)的状态(已知)和当前的输入\(u_{k}\)(已知，如果有的话)，直接估计出当前时刻的可能状态\(\hat{x}^{-}_{k}\)。这个过程和是否观测无关。进一步，我们可以发现，红色框框中的这两部分都是一样的，它们对应的都是根据上一时刻状态和当前时刻输入得到的先验估计值。这也是和State Observer式子式吻合的。所以简化一下，就可以写成黑色方框中的式子了。可以看到，在式子的后半部分，我们利用已经得到的对当前状态的估计\(\hat{x}^{-}_{k}\)和当前的观测\(y_{k}\)，来更新我们的先验估计。这句话可能有点绕口，多读几遍就理解了。最终我们就可以得到更新之后的先验估计，这个结果就被称为后验估计。小结一下就是：我们把根据上一时刻状态和当前时刻输入，利用模型计算当前时刻状态的步骤叫做预测(Predict)，把初步预测结果和当前时刻的观测融合的步骤叫做更新(Update)，把由他们计算得到当前时刻的状态的最优估计称为后验估计(Posteriori Estimate)。

因此，最终，一个完整的Kalman Filter需要用到的公式如下。 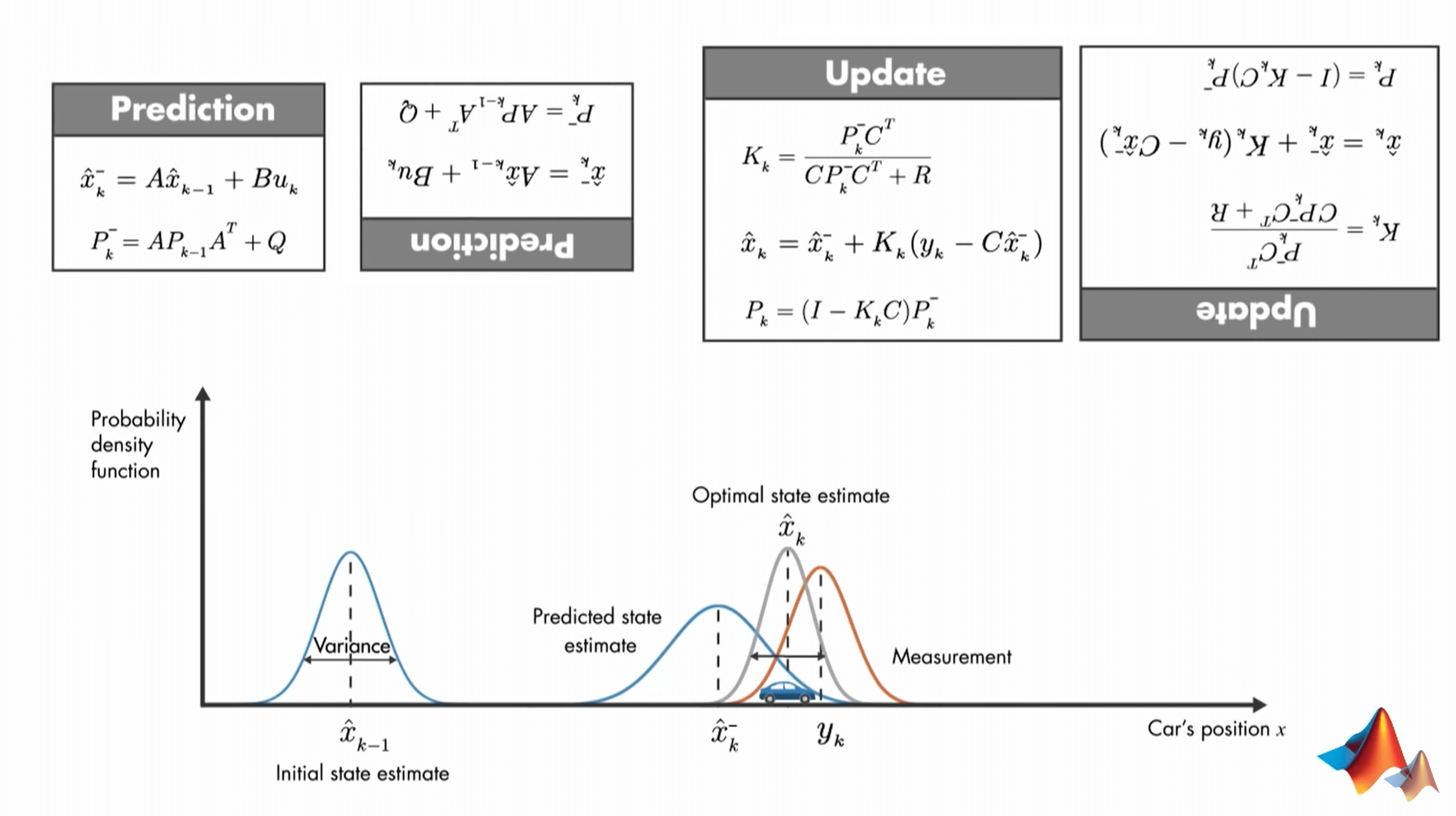这些式子看起来就十分复杂和令人害怕，即使把它们反过来也好不到哪去(作者开的小玩笑)。正如上面所说，Kalman Filter是一个时序的算法，这些公式之间也是有先后顺序关系的。因此我们不能直接一股脑地阅读，这样不容易理解和找到逻辑关系。可以按照如下步骤理解。

首先要记住，Kalman Filter包含两步：预测(Predict)与更新(Update)。这里有几个问题需要回答：

• 预测什么？拿什么预测？
• 更新什么？拿什么更新？

简单依次回答一下。预测的是当前时刻的状态，用的是上一时刻的估计值和当前时刻的输入(如果有的话)。更新的是我们刚刚预测的结果，用的是预测结果和测量值。明确了这两个概念后，就可以往下看了。 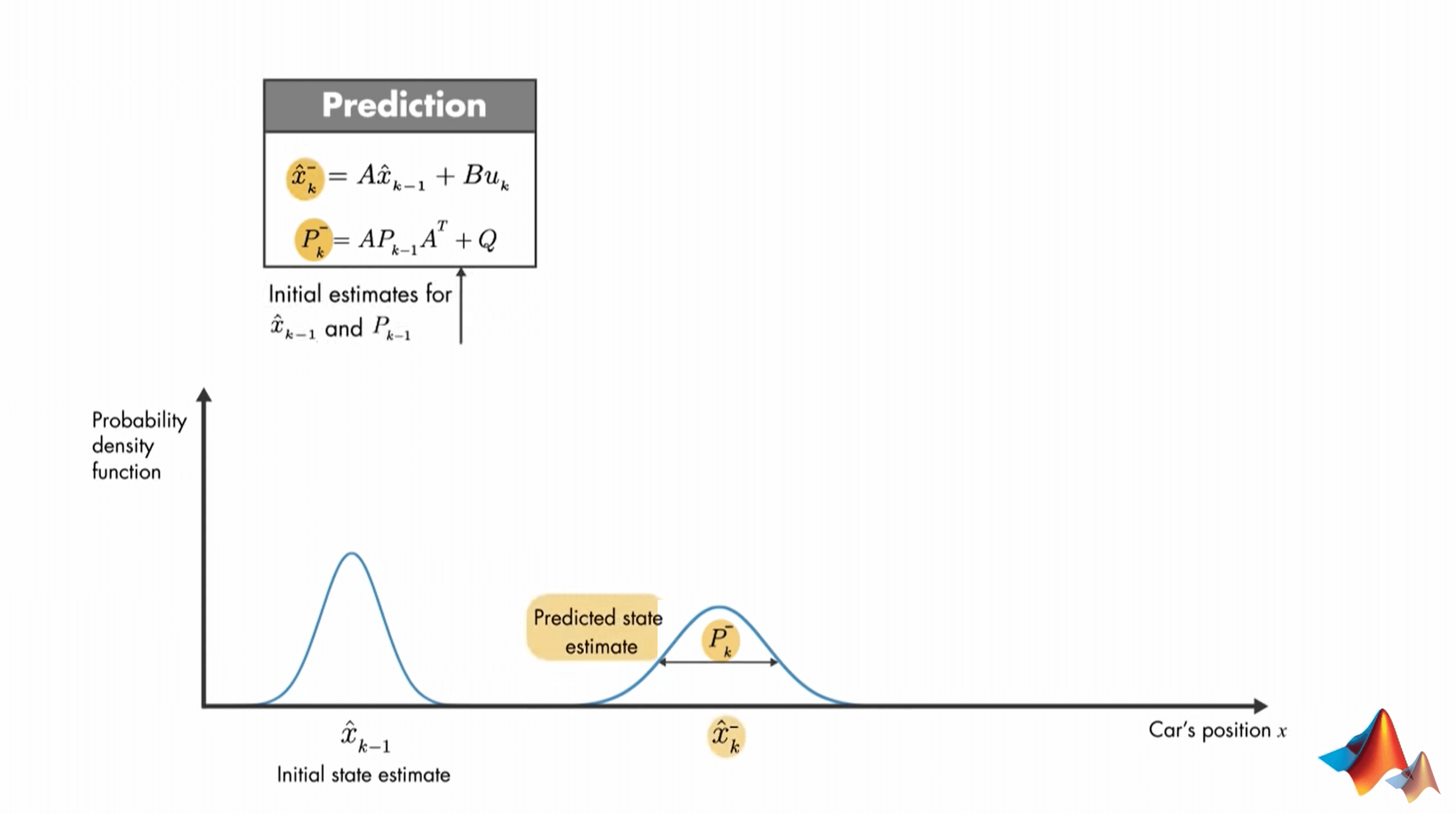首先在预测(Prediction)步骤，我们需要计算当前状态的先验估计(Priori Estimate)以及估计值的方差/协方差。对于第一个式子，就是我们之前说了很多遍的，利用上一时刻的状态和当前时刻的输入(如果有的话)进行估计，得到当前状态的初始估计值\(\hat{x}^{-}_{k}\)。第二个式子可以计算估计的不确定性，用于不确定性度量。根据这个式子，我们也可以看出来，这种不确定性来自于两方面，一是外部过程噪声，另一个是上一个状态本身存在的噪声。公式中各个变量的含义这里简单说一下。\(A\)、\(B\)都是状态转移方程中表示上一状态、输入和当前状态之间关系的变量，在建模时就确定，在后续迭代中保持不变。\(Q\)是状态转移方程中的噪声\(w_{k}\)服从的高斯分布的方差/协方差，同样是在建模时确定，可看作常量。最后，你可能会有疑问，你的预测都是基于上一时刻的状态和不确定性，那系统一开始，哪来的初始值呢？一般而言，在算法的最开始，都会给定状态和不确定性的初始值(相当于是\(\hat{x}^{-}_{0}\)和\(P_{0}\))。 然后就是更新(Update)步骤。显然，仅仅靠先验估计得到的结果是不准确的，但我们还有观测值。可以用它来进一步更新和校正预测结果。与预测步骤对应的，我们同样需要计算两个部分，一是估计的状态，而是不确定性。首先，我们要先用预测步骤得到的\(\hat{P}^{-}_{k}\)计算卡尔曼增益\(K_{k}\)，它可以使更新后的状态值方差/协方差最小。有了它以后，再结合我们预测得到的先验估计结果\(\hat{x}^{-}_{k}\)、观测值\(y_{k}\)就可以得到更新以后的后验估计值\(\hat{x}_{k}\)。最后，同样利用预测得到的\(\hat{P}^{-}_{k}\)和刚算出来的卡尔曼增益\(K_{k}\)就可以得到更新以后的新的不确定性\(P_{k}\)。另外说一点，公式里的变量比较多，因此需要先弄懂各个含义，以及已知量和未知量。首先是第一个公式里的\(C\)，它来自于我们一开始模型的观测方程，用于表示我们的观测值与估计值之间的关系。而\(R\)同样来自观测方程，是噪声\(v_{k}\)服从的高斯分布的方差/协方差，表示不确定度。对于第一个公式，\(C\)、\(R\)可以看作是常量，在模型建立的时候就确定的。\(P\)是变量，随着迭代而改变，表示每次先验估计的不确定性。在公式二中，只有\(C\)是常量。\(\hat{x}^{-}_{k}\)是先验估计值，\(y_{k}\)是观测值，\(K_{k}\)是每次迭代的卡尔曼增益。在公式三中，常量同样只有\(C\)。变量是先验估计的不确定性\(\hat{P}^{-}_{k}\)和卡尔曼增益\(K_{k}\)。 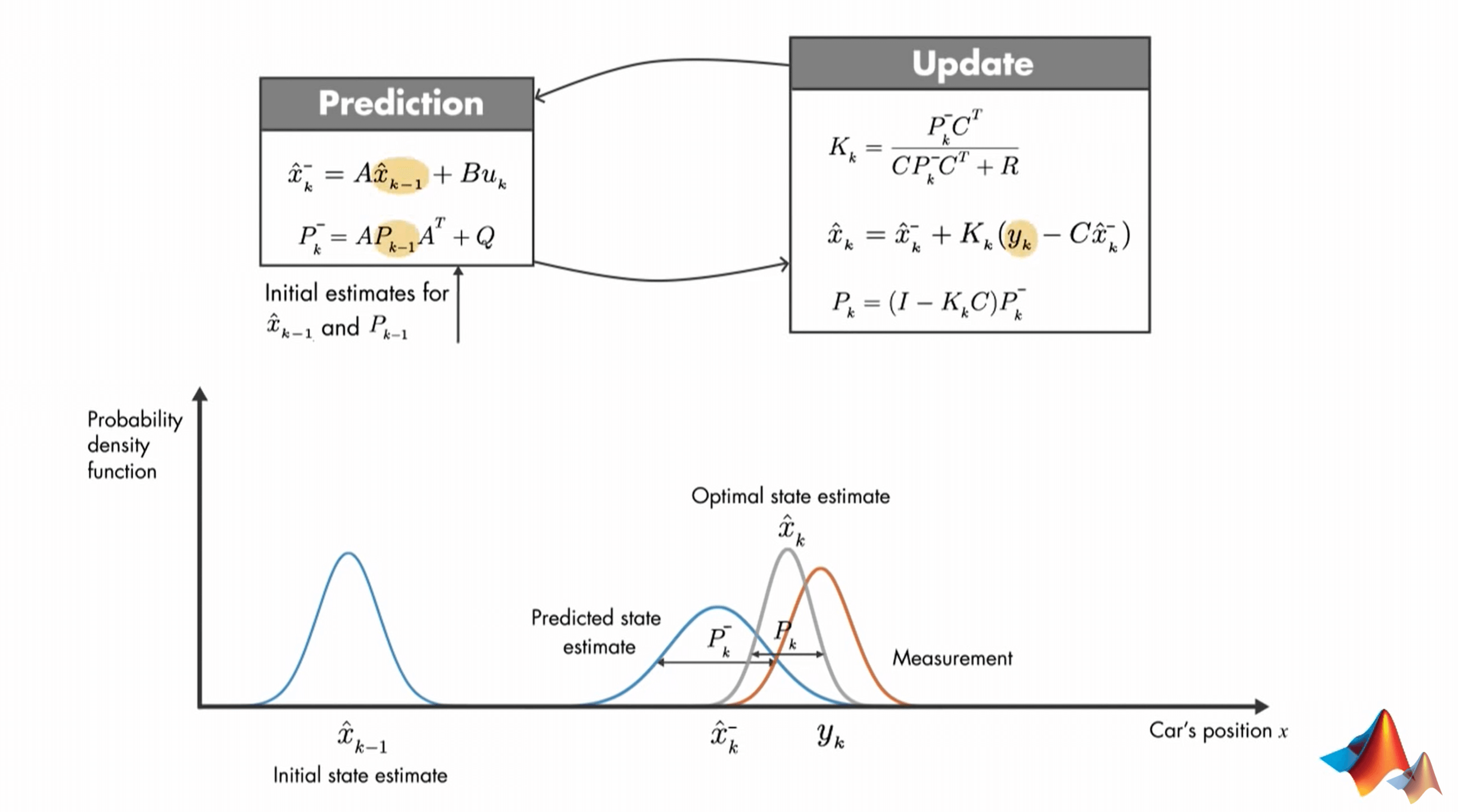这样，一个完整的Kalman Filter步骤就完成了。后面就是再将更新后的结果传入下一次预测步骤，形成一个环，一直循环下去。我们只需要上一个时刻的估计状态、不确定性(方差/协方差)，以及当前时刻的观测，将其输入Kalman Filter，就可以不断迭代，形成一个“永动机”。此外，可以看到，我们最终的结果是由观测值和估计值共同决定的。很自然地我们会想到，如果观测值的不确定性较小，它就应该有较大的权重，反之亦然。事实上，Kalman Filter就是这样做的。我们不妨讨论两种极端情况。首先，如果我们认为测量是完全准确的。那么也就是说，\(v_{k}\)没有误差，它的方差/协方差\(R\)为0。那么这个时候，可以分别推导出\(K_{k}\)、\(\hat{x}_{k}\)、\(P_{k}\)的表达式如下。 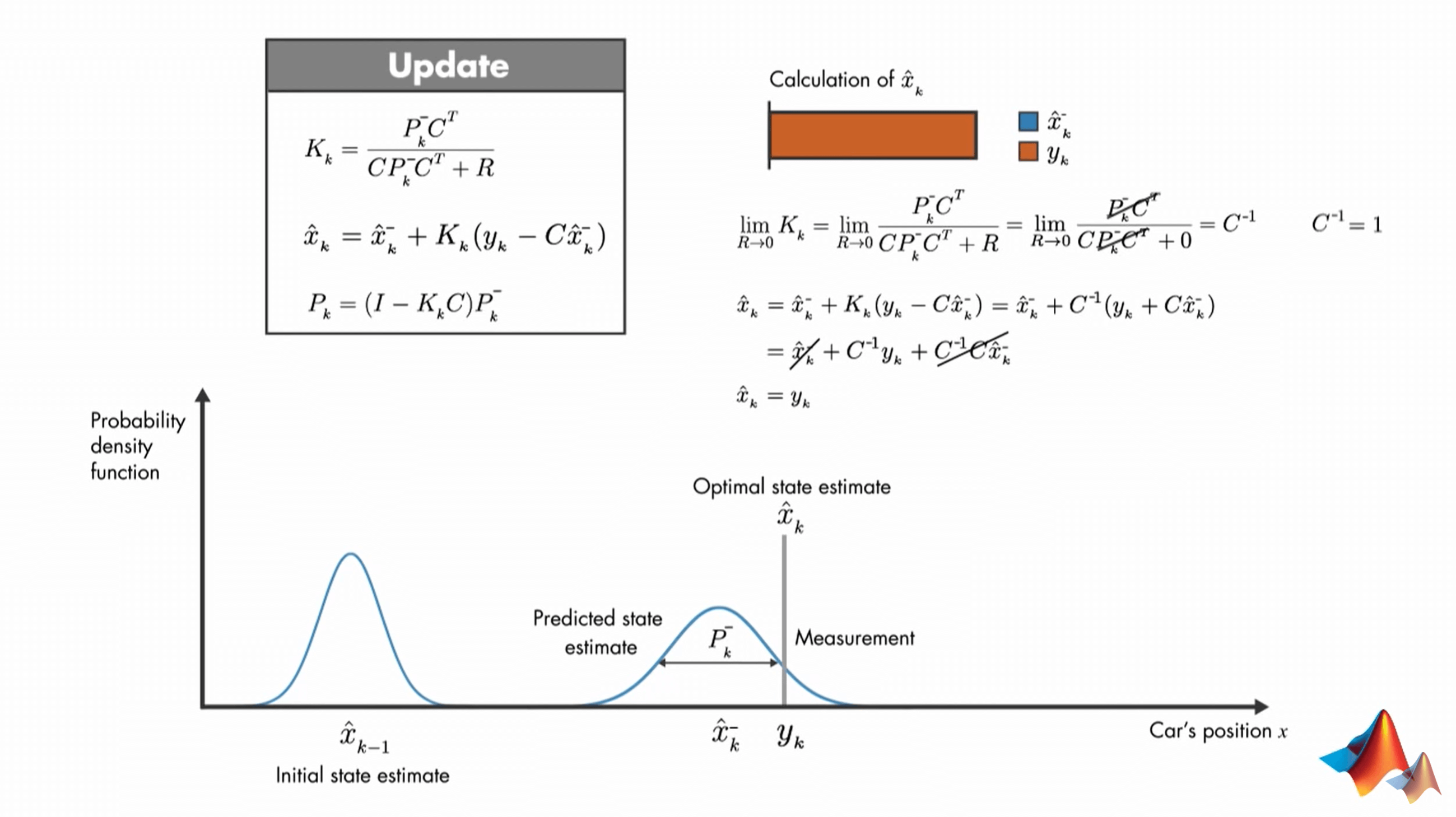可以看到，我们最优的估计值就变成了\(y_{k}\)。同理，如果我们认为预测值是完全准确的，那么就有下图所示的公式。 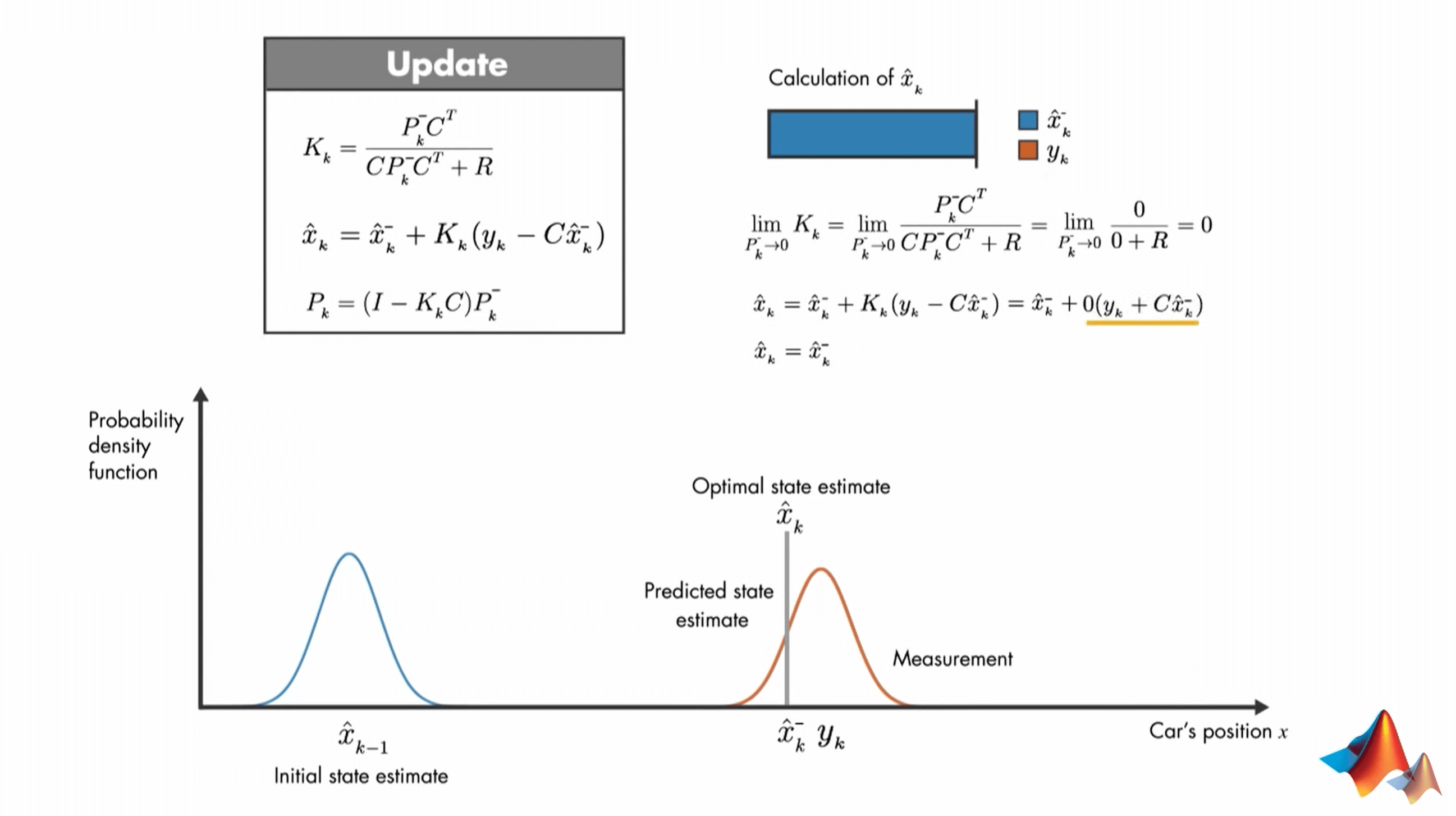可以看到，最优估计就变成了预测值。而这种变化其实都是由卡尔曼增益\(K_{k}\)的变化引起的。当\(K_{k}\)等于1时，完全详细观测值，当\(K_{k}\)等于0时，完全相信预测值。\(K_{k}\)决定了它们两者在融合时候的权重。

最后，Kalman Filter也被称为Sensor Fusion Algorithm(传感器融合算法)。上面的例子中，我们只有一个观测值，但事实上我们可能有多个传感器提供多个观测值，如GPS和IMU同时提供位置信息。那么这个时候，当我们有两个观测值、一个估计状态的时候，公式的维度会变成下面这样。 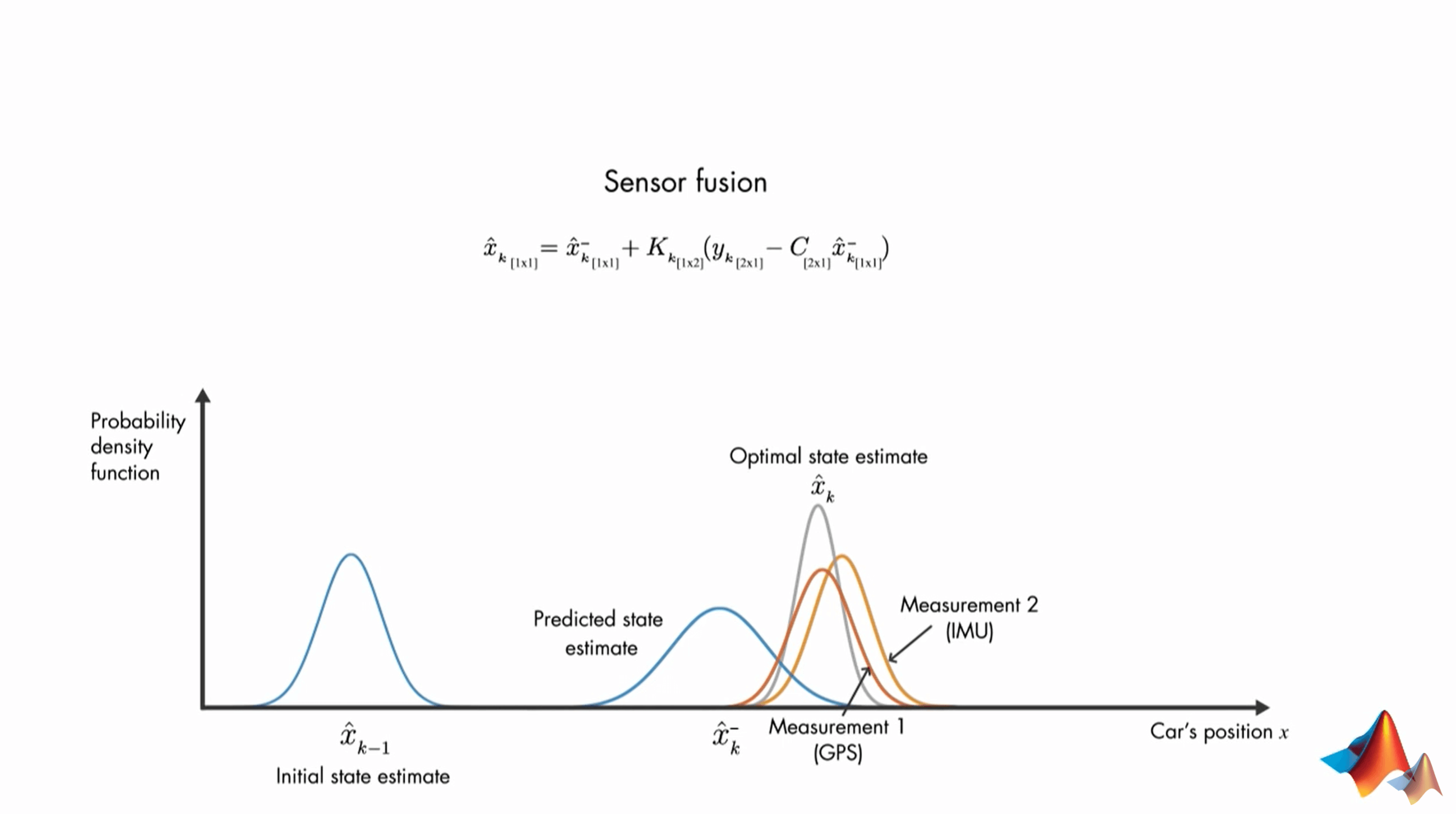如果你细心的话会发现，上面这些建模都是线性的，但在实际应用中非线性的情况大量存在。因此需要新的手段进行处理。这会在下一讲介绍。

5.Nonlinear State Estimators

第五讲视频在这里，点击查看。视频一开头就说出了一个残酷的现实。 我们希望很多事情是线性发展的，但事实上很多事情都是非线性的。在前面我们介绍的Kalman Filter是针对于线性系统的，从它的公式中就可以看得出来。 比如，对于上面的例子而言，当我们引入道路摩擦等种种因素后，状态转移方程和观测方程都有可能变成非线性。对于Kalman Filter而言，其假设服从高斯分布，高斯分布对于一个线性变换，变换以后仍然是高斯分布，但是如果是非线性变换，变换之后就可能不再是高斯分布。这种情况下Kalman Filter的假设条件就被打破，可能出现不收敛的情况。 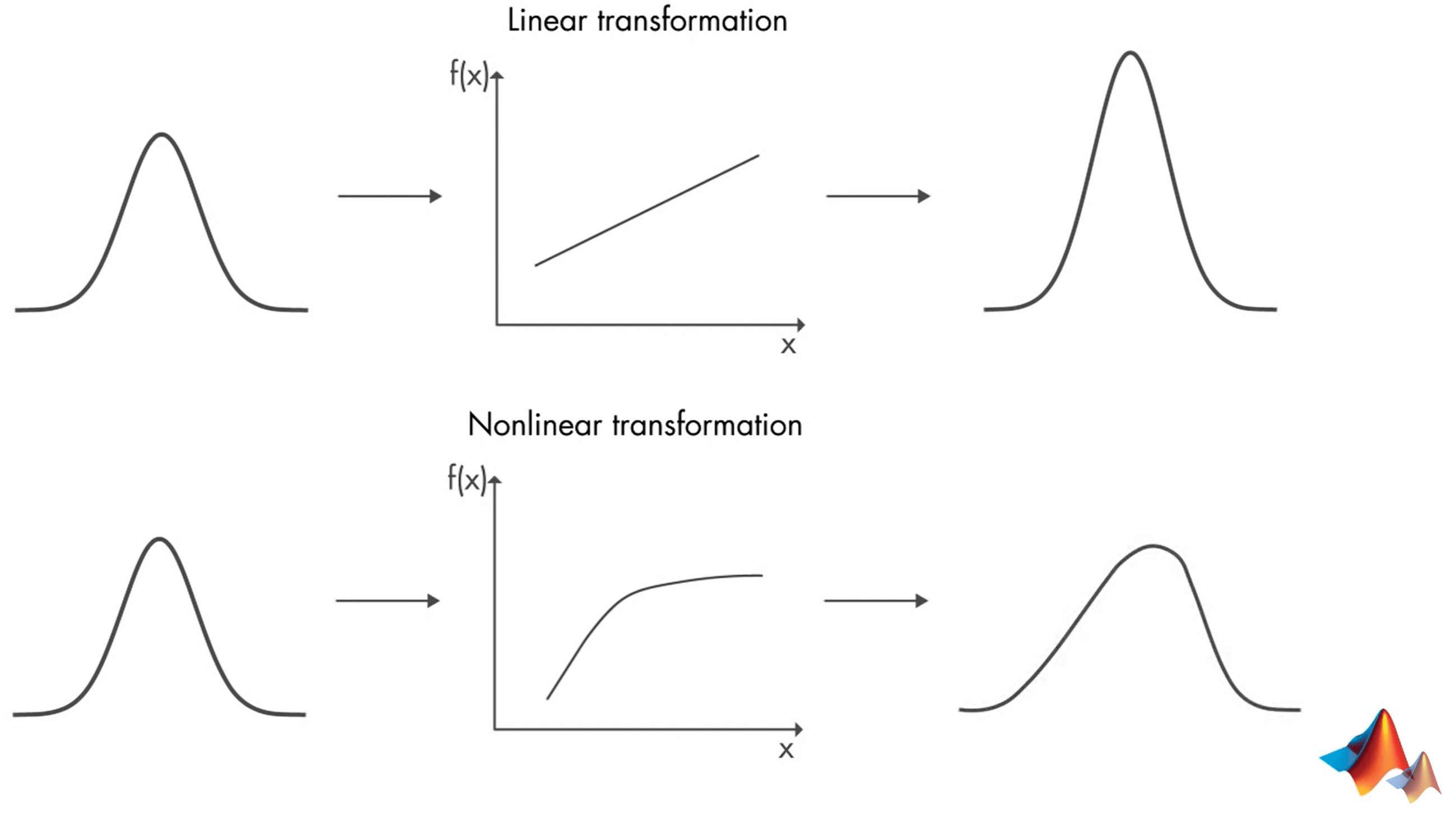所以我们需要研究非线性的Kalman Filter。一个可行的办法是，在非线性变换的局部进行线性化，然后我们又可以“愉快地”使用Kalman Filter了。这种使用Kalman Filter的思想就叫做Extended Kalman Filter(扩展卡尔曼滤波)。 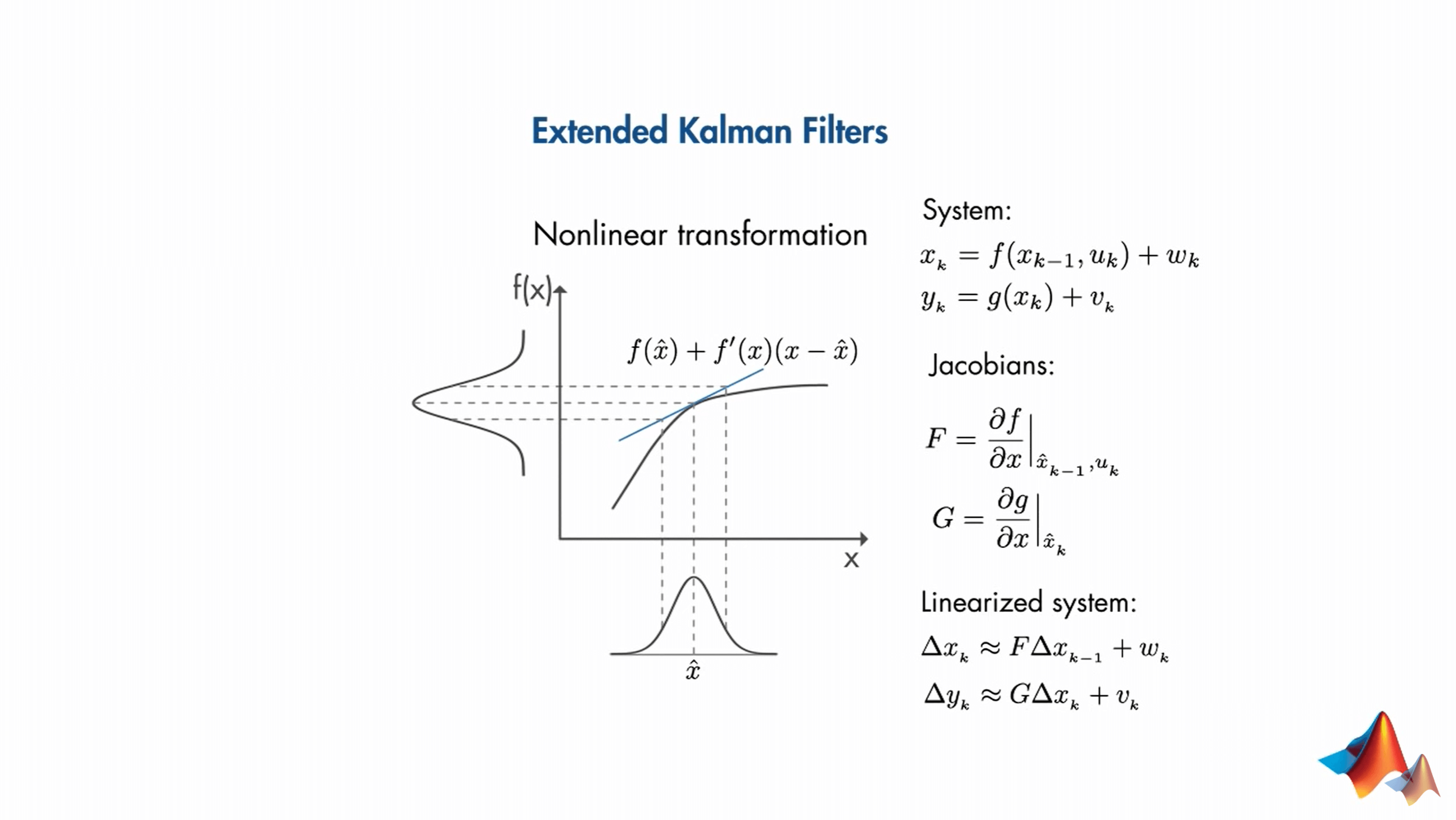它把非线性函数在当前估算状态的平均值附近进行线性化。在每一步执行线性化，然后将得到的雅可比矩阵用于预测和更新卡尔曼滤波器算法的状态。而且如果你仔细观察的话会发现，EKF使用的线性化方法是一阶Taylor展开。因此，当系统是非线性，并且可以通过局部线性化很好地近似时，EKF就是一个状态估算很好的选择。但是，它也有如下列出的缺点： 除了计算复杂度较高之外，一个比较大的问题是当系统高度非线性化的时候，EKF并不能起到很好的作用。比如上面的这个图中的非线性对应关系就无法被很好地局部线性化。针对这个问题，一种新的Kalman Filter被提出来了，那就是Unscented Kalman Filter(UKF，无迹/无香卡尔曼滤波)。 你可能会奇怪，为什么要叫这么一个奇怪的名字。视频中也给了解释。没什么特别的原因，因为作者看到同事桌上的一个除臭剂，所以想到了这个名字。它和EKF最大的区别在于，EKF利用Taylor公式在局部近似非线性函数，而UKF则是尝试近似概率分布。 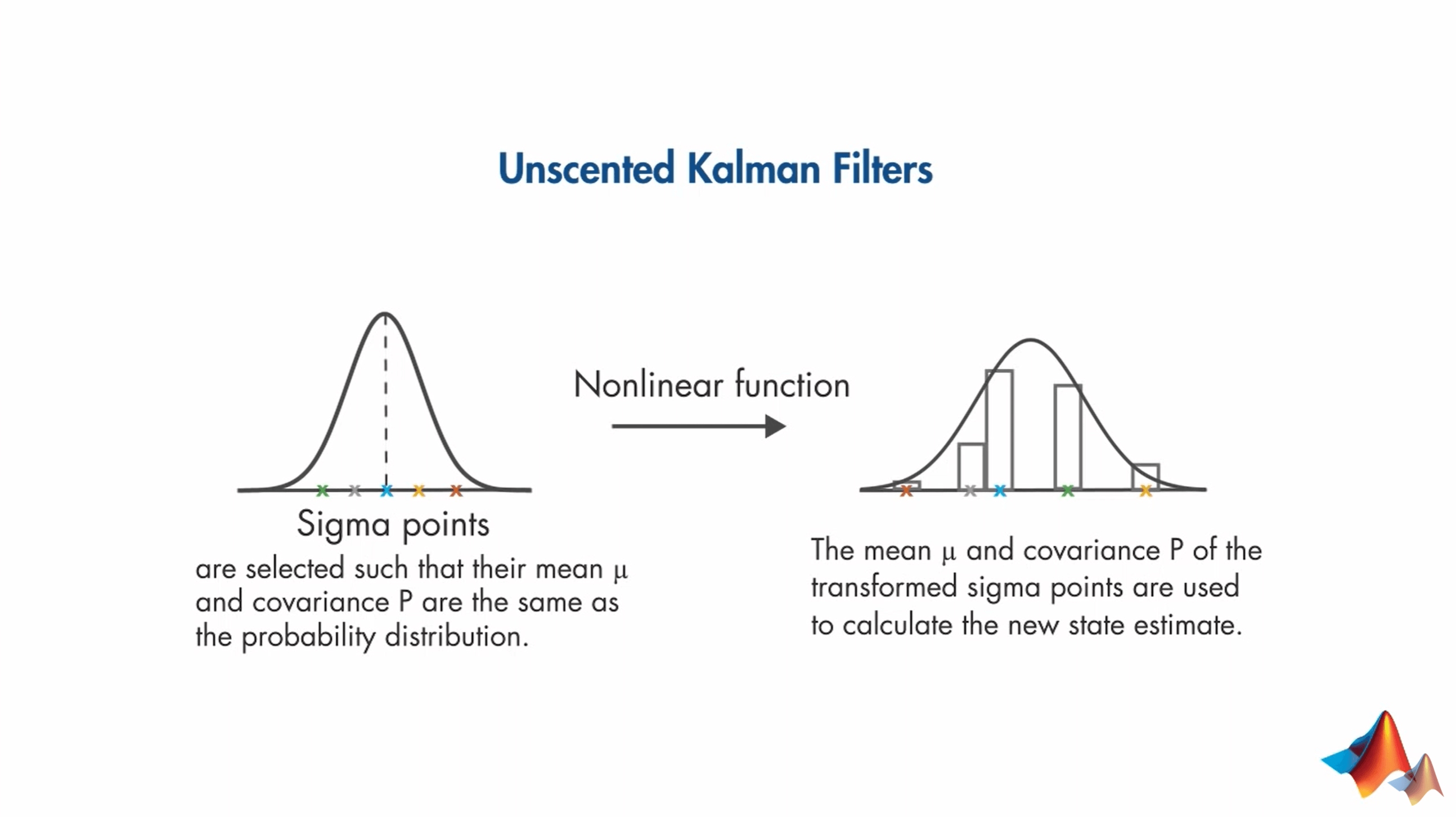前面说了UKF近似概率分布。具体来说，就是我们选择一组最小的采样点，让它们的均值和方差与目标分布相同。这些采样点被称为Sigma点，并且围绕均值对称分布。然后，每一个Sigma点都通过非线性系统模型进行计算，并计算非线性变换后的输出点的均值与协方差，计算经验高斯分布(Empirical Gaussian Distribution)。这个新的计算得到的高斯分布，就是我们想要得到的：这个新的高斯分布的均值就是新的状态估计值，方差就是不确定程度。这种计算方式和前面提到的KF的方式是不同的。在KF中，我们在预测阶段使用状态转移函数计算误差/协方差\(P\)，并在更新阶段用测量量进行更新。但在UKF中，如上面所说，是根据经验方法(Empirical)算出来的高斯分布。这里需要说明的一点是与KF一样，UKF仍然是基于高斯分布的，所以当Sigma点变换以后，我们最终拟合得到的还是一个高斯分布。

此外，还有另一种和UKF类似的非线性状态估计器(Nonlinear State Estimator)就是Particle Filter(粒子滤波)。 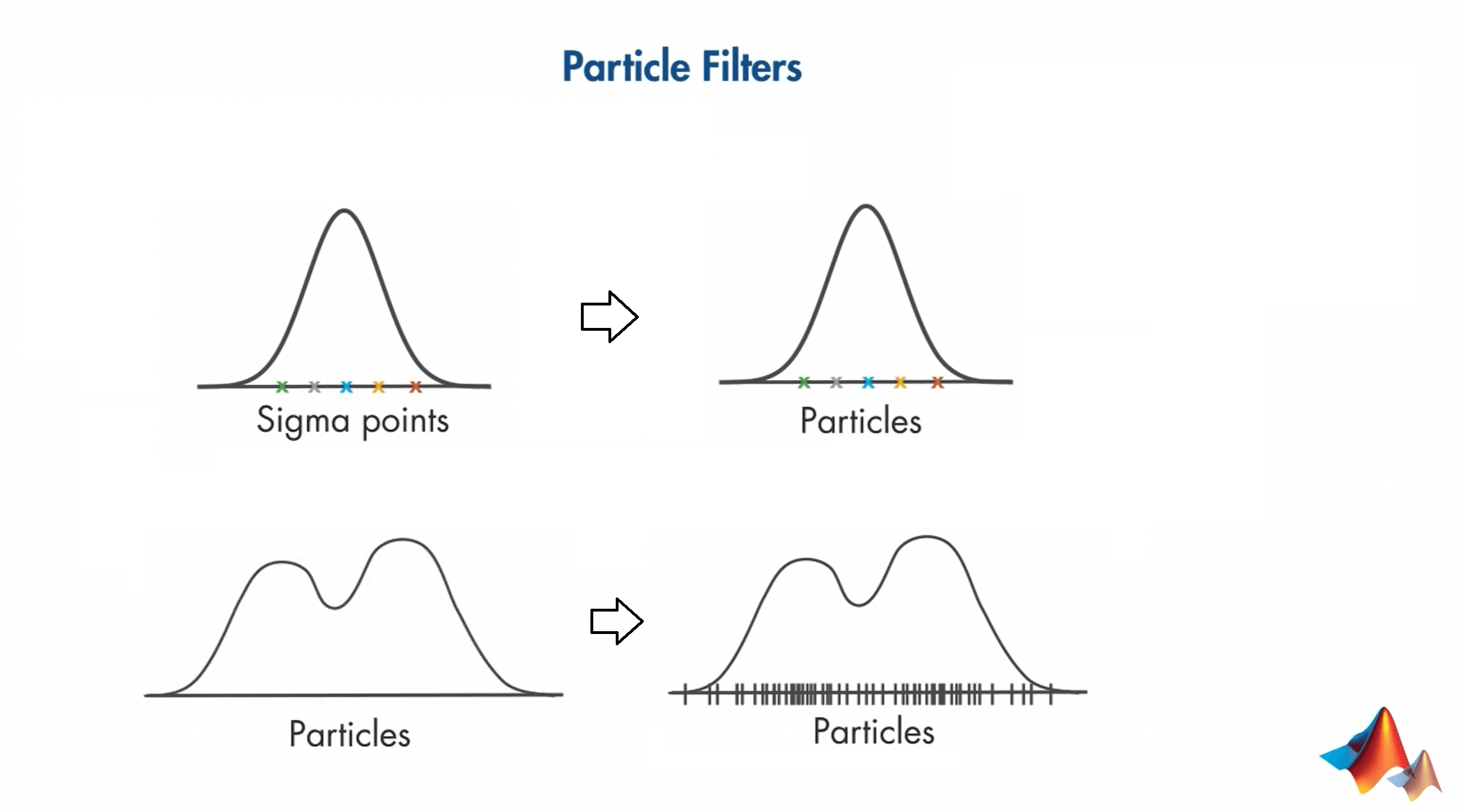PF和UKF的相似之处在于它们都使用采样点才拟合概率分布。不同之处则在于：一是PF去除了对于分布必须是高斯的这个假设，其可以拟合任意分布；二是由于去除了对于分布的假设，因此对于一个位置的分布，必须要使用使用比UKF多得多的采样点。在UKF中，这种采样点叫做Sigma点，在PF中，它们叫做粒子。

最后，对上面提到的KF、EKF、UKF以及PF进行小结，如下。 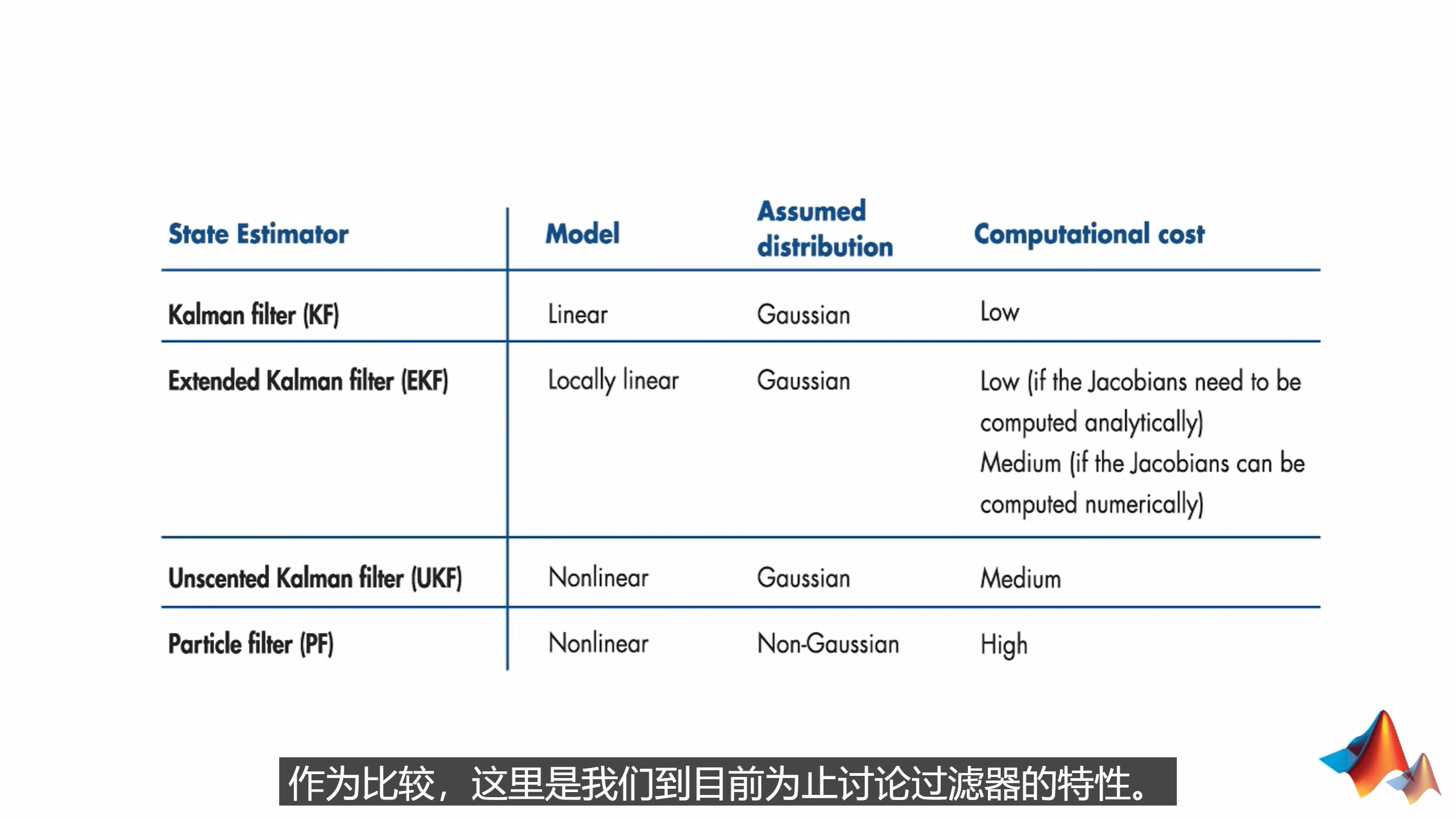可以看到，KF适合于线性系统，而EKF适合于可以局部线性化的非线性系统。UKF和PF则适合于任意非线性系统。从假设的分布而言，KF、EKF和UKF都假设分布是高斯的，只有PF适合于非高斯分布。对于计算开销而言，表格越往下计算开销越大。PF因为需要大量的粒子来近似任意分布，所以计算量是最大的。因此，如果你可以确定一个系统是高斯分布的，就完全没有必要用PF了。

6.Reference

• [1] https://youtube.com/playlist?list=PLn8PRpmsu08pzi6EMiYnR-076Mh-q3tWr