1.卡尔曼滤波适合什么任务场景
卡尔曼滤波特别适合两种任务和场景:
- 感兴趣的变量无法直接观测,需要通过一个或多个带有噪声的观测量计算得到,通过卡尔曼滤波可给出感兴趣变量的最优估计。
- 有多个传感器同时观测,需要做传感器数据的动态融合,通过卡尔曼滤波可给出最优融合结果。
如果你的任务和需求符合上面的任意一点,那么卡尔曼滤波就适合你。可以继续回答下面问题。
2.使用卡尔曼滤波前需明确的内容
在使用卡尔曼滤波解决问题时,如果能够回答清楚下面的问题,使用卡尔曼滤波就比较清晰了。
2.1 观测量是什么
实际观测内容是什么,有几个?
一般而言,对于\(m\)个观测量,对应观测向量\(\mathbf{z}\)大小为\(m \times 1\)。
例如,用一个传感器观测了火箭发动机外部温度\(T_{e}\),基于它可构成观测向量\(\mathbf{z} = [T_{e}]\)。
2.2 希望估计的量是什么
你希望用卡尔曼滤波得到关于什么量的最优估计?有几个?
一般而言,对于\(n\)个估计量,对应状态向量\(\mathbf{x}\)大小为\(n \times 1\)。
例如,希望得到关于火箭发动机内部温度\(T_{i}\)的最优估计。那么这个内部温度\(T_{i}\)就是希望估计的状态向量\(\mathbf{x} = [T_{i}]\)。
2.3 状态间存在什么关联
基于你的状态定义,从上一个时刻到下一个时刻,状态是否随时间变化?
注意这里抓住“随时间变化”,“时间”这个自变量。随时间变化那就写出对应关系(线性增加或减少),不变那么上一个状态就和下一个状态相等。一般而言,对于\(n \times 1\)的状态向量,其对应的状态转移矩阵\(\mathbf{F}\)大小为\(n \times n\)。在标准卡尔曼滤波中,状态转移矩阵\(\mathbf{F}\)作为描述系统动态的先验知识,不随滤波过程变化。
例如,火箭平稳飞行时发动机内部温度基本保持不变,所以\(t\)时刻的外部温度\(T_{e}^{t}\)和\(t-1\)时刻的外部温度\(T_{e}^{t-1}\)相等,有\(T_{e}^{t} = 1 \cdot T_{e}^{t-1}\),这里的系数即为状态转移矩阵\(\mathbf{F}\)。
2.4 系统状态是否有外部因素控制
除系统状态\(\mathbf{x}\)本身随时间的演化,是否有外部因素干预?如果有,有几个,其和系统状态间的数学关系是什么(线性表达)?
一般而言,对于\(k\)个外部控制量,对应控制输入向量大小为\(k \times 1\)。又因为控制输入直接作用于大小为\(n \times 1\)系统状态向量\(\mathbf{x}\),因此控制输入矩阵\(\mathbf{B}\)大小为\(n \times k\),其中的元素\(b_{ij}\)表示第j个控制输入对第i个状态变量的直接影响强度。在标准卡尔曼滤波中,控制输入矩阵\(\mathbf{B}\)作为描述系统控制的先验知识,不随滤波过程变化。
例如,火箭发动机温度受油门影响,油门大则燃料充足,发动机温度升高,反之亦然。假设油门和温度的关系是每增加1油门,温度升高100度。那么这里,控制输入向量\(\mathbf{u}\)即为油门,其对应的控制输入矩阵\(\mathbf{B} = [100]\)。
2.5 状态和观测之间存在什么关联
基于你给定的观测\(\mathbf{z}\)和状态\(\mathbf{x}\),两者间是否有数学上的关系(基础卡尔曼滤波认为只存在线性关系)?
一般而言,对于\(m \times 1\)的观测向量和\(n \times 1\)的状态向量,其对应的观测矩阵\(\mathbf{H}\)大小为\(n \times m\)。在标准卡尔曼滤波中,观测矩阵\(\mathbf{H}\)作为描述状态和观测间关联的的先验,不随滤波过程变化。
例如,假设地面实验已知,发动机外部温度\(T_{e}\)与内部温度\(T_{i}\)存在\(T_{e} = 0.5 \cdot T_{i}\)关系。这里的系数即为观测矩阵\(\mathbf{H}\)。这里需要特别注意的是,观测矩阵是从状态到观测的系数,不能反了。
2.6 实际观测量的误差怎么样
基于你给定的观测量,传感器的实际误差怎么样(一般用方差表示)?
对于单个观测量用单个方差表示,对于多个变量用协方差矩阵表示即可。协方差矩阵对角线元素为各变量的方差。一般而言,对于\(m \times 1\)的观测向量,其对应的协方差矩阵\(\mathbf{R}\)大小为\(m \times m\)。
例如,假设发动机外部传感器的温度测量方差为0.5,那么测量噪声协方差矩阵为\(\mathbf{R} = [0.5]\)。
2.7 运行过程外部干扰怎么样
在运行过程中,是否存在一些难以建模的外部干扰因素,如果有误差怎么样(一般用方差表示)?
一般而言,对于\(n \times 1\)的状态向量,其对应的过程噪声协方差矩阵\(\mathbf{Q}\)大小为\(n \times n\)。
例如,火箭发动机运行过程中剧烈振动可能导致外部温度传感器松动造成测量结果不准,假设导致一个方差为0.1的误差,那么过程噪声协方差矩阵\(\mathbf{Q} = [0.1]\)。
2.8 初始预测状态怎么样
在系统第一次运行的时候,预测的状态是什么,对应的误差是多少?
对于初始预测状态,一般会基于第一个观测和理论上的观测矩阵计算得到。对于初始预测误差,一般会将其设为一个较大的数值,在后续滤波过程中会自动迭代更新。一般而言,对于\(n \times 1\)的状态向量,其对应的状态协方差矩阵\(\mathbf{P}\)大小为\(n \times n\)。
例如,假设外部温度\(T_{e}\)的第一个观测数值\(\mathbf{z}\)为100度,根据观测矩阵\(\mathbf{H}\),可以得到第一个初始预测状态\(\mathbf{x}\)为200。对应状态协方差矩阵可设置一个较大的值,例如\(\mathbf{P} = [1]\)。
3.卡尔曼滤波核心步骤
3.1 变量说明
常量参数
以下参数在卡尔曼滤波启动前就可以给定,滤波过程中不会改变:
- 状态转移矩阵\(\mathbf{F}\)
- 观测矩阵\(\mathbf{H}\)
- 控制输入矩阵\(\mathbf{B}\)
- 过程噪声协方差矩阵\(\mathbf{Q}\)
- 测量噪声协方差矩阵\(\mathbf{R}\)
初始值
卡尔曼滤波作为迭代算法,预测t时刻状态需要知道t-1时刻的状态和误差。因此,在系统刚启动时,需要手动对迭代变量赋值,以便可以进行后续计算:
- 初始状态估计向量\(\mathbf{x}\):一般设为第一个观测值
- 初始状态协方差矩阵\(\mathbf{P}\):一般设为较大的数
这两个变量在后续迭代过程中都会自动更新。
持续输入
在运行过程中,需要不断输入当前的观测和控制作为状态预测起算数据,卡尔曼滤波基于当前输入和上一时刻状态进行计算。
- 控制输入向量\(\mathbf{u}\)
- 实际观测向量\(\mathbf{z}\)
持续输出
卡尔曼滤波可以给出当前时刻的最优估计,主要包括状态和误差:
- 当前最优估计的状态向量\(\mathbf{x}\)
- 当前估计状态对应的状态协方差矩阵\(\mathbf{P}\)
3.2 预测(状态预测)
- Step1. 根据上一个状态,结合给定模型,预测当前时刻状态:
- Step2. 根据给定误差和上一状态误差,计算当前时刻预测状态对应的误差:
3.3 更新(测量更新)
- Step3. 根据上一状态预测误差、给定的观测误差和观测矩阵,计算卡尔曼增益(这里括号外的-1对于标量表示分数,对于矩阵表示求逆):
- Step4. 根据当前预测状态、实际观测和观测矩阵,结合卡尔曼增益平衡预测与观测权重,修正状态预测:
- Step5. 根据计算得到的卡尔曼增益、上一个状态预测误差、给定的观测矩阵,计算修正后状态对应的误差:
4.实际示例
4.1 一维位置估计
4.1.1 问题描述
一个人以0.2m/s恒定速度在一维空间中向前移动,观测他的位置\(p\),利用卡尔曼滤波估计他的最优位置。本示例中,观测量就是状态量。
4.1.2 问题建模
问题建模可以从前面几个问题开始:
观测量是什么:人的位置\(p\),观测向量\(\mathbf{z} = [p]\)。
希望估计的量是什么:人在某个时刻的最优位置,状态向量\(\mathbf{x} = [p]\)。
状态间存在什么关联:人做匀速运动,而根据状态定义即为位置。假设两个状态间的时间差异为\(\Delta t\),理论上有\(\mathbf{x}_t = \mathbf{x}_{t-1} + 0.2 \cdot \Delta t\)。这里的系数即为状态转移矩阵\(\mathbf{F} = [1]\)。
系统状态是否有外部因素控制:无。控制输入向量\(\mathbf{u}\)为0,其对应的控制输入矩阵\(\mathbf{B} = [0]\)。
状态和观测之间存在什么关联:因为观测是位置,状态也是位置,所以\(\mathbf{z} = 1 \cdot \mathbf{x}\),这里的系数即为观测矩阵\(\mathbf{H} = [1]\)。
实际观测量的误差怎么样:假设实际位置测量方差为2.0,那么测量噪声协方差矩阵为\(\mathbf{R} = [2.0]\)。
运行过程外部干扰怎么样:假设存在不可预知的大风、下雨等因素导致速度变化,假设导致一个方差为0.5的误差,那么过程噪声协方差矩阵\(\mathbf{Q} = [0.5]\)。
初始预测状态怎么样:假设第一个观测数值\(\mathbf{z}\)为0、第一个初始预测状态\(\mathbf{x}\)为0。对应状态协方差矩阵可设置一个较大的值,例如\(\mathbf{P} = [1]\)。
基于以上答案,便可构建基本变量和卡尔曼滤波核心步骤:
- 状态转移矩阵\(\mathbf{F} = [1]\)
- 观测矩阵\(\mathbf{H} = [1]\)
- 控制输入矩阵\(\mathbf{B} = [0]\)
- 过程噪声协方差矩阵\(\mathbf{Q} = [0.5]\)
- 测量噪声协方差矩阵\(\mathbf{R} = [2.0]\)
- 初始状态估计向量\(\mathbf{x} = [0]\)
- 初始状态协方差矩阵\(\mathbf{P} = [1]\)
- 输入:控制输入向量\(\mathbf{u}\)
- 输入:实际观测向量\(\mathbf{z}\)
- 输出:当前最优估计状态向量\(\mathbf{x}\)
- 输出:当前状态对应的状态协方差矩阵\(\mathbf{P}\)
4.1.3 代码实现
基于上面给出的公式和确定的参数,最终,可以通过以下代码实现卡尔曼滤波。
import numpy as np
import matplotlib.pyplot as plt
# 一维位置估计 - 基础卡尔曼滤波演示
# 一个人以0.2m/s恒定速度在一维空间中向前移动,观测他的位置50秒
# 给定参数
H = 1 # 观测矩阵
F = 1 # 状态转移矩阵
B = 0 # 控制输入矩阵
Q = 0.5 # 过程噪声协方差矩阵
R = 2.0 # 测量噪声协方差矩阵
# 指定理论值,方便评估精度,实际无法获得
true_values = []
for i in range(50):
true_values.append(i*0.2) # 真实位置为0到10之间
true_values = np.array(true_values, dtype=float)
# 系列观测与控制输入
np.random.seed(0)
z = true_values + np.random.normal(0, 1, size=len(true_values))
u = np.zeros_like(z)
# 给状态赋初值
prev_state = z[0]
prev_error = 1.0
# 用于存放估计的状态
predict_states = []
# 卡尔曼滤波过程
for i in range(len(z)):
# 预测 - 状态
predict_state = F * prev_state + B * u[i]
# 预测 - 误差
predict_error = F * prev_error * F + Q
# 更新 - 卡尔曼增益
kalman_gain = (predict_error * H) / (H * predict_error * H + R)
# 更新 - 状态
update_state = predict_state + kalman_gain * (z[i] - H * predict_state)
# 更新 - 误差
update_error = (1 - kalman_gain * H) * predict_error
# 变量赋值开启下次迭代
prev_state = update_state
prev_error = update_error
# 将预测状态保存起来
predict_states.append(update_state)
# 精度评价
error_measure = np.mean(np.abs(z - true_values))
error_kalman = np.mean(np.abs(predict_states - true_values))
print("Mean Error of Measurements:", error_measure)
print("Mean Error of Kalman Filter:", error_kalman)
# 可视化结果
plt.figure(figsize=(10,6))
plt.plot(true_values, np.zeros_like(true_values), label='True Values', linestyle='--')
plt.plot(true_values, z - true_values, label='Noisy Measurements', marker='o', markersize=4)
plt.plot(true_values, predict_states - true_values, label='Kalman Filter', linewidth=2)
plt.legend()
plt.xlabel('Time Step')
plt.ylabel('Value')
plt.title('Basic Kalman Filter Demo')
plt.show()
运行后效果如下:
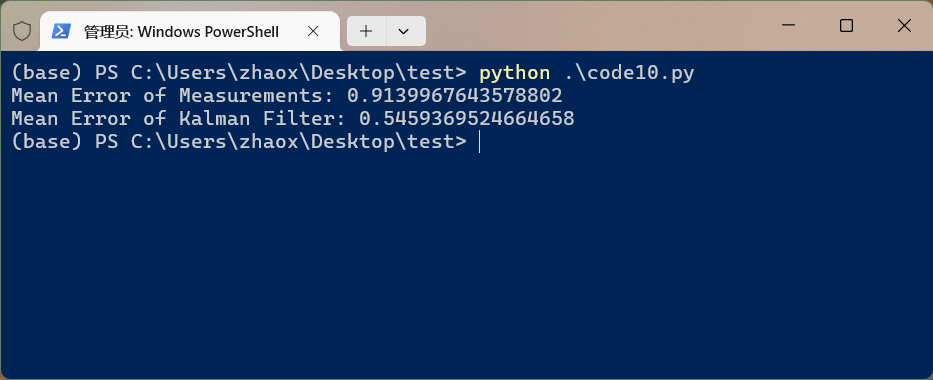
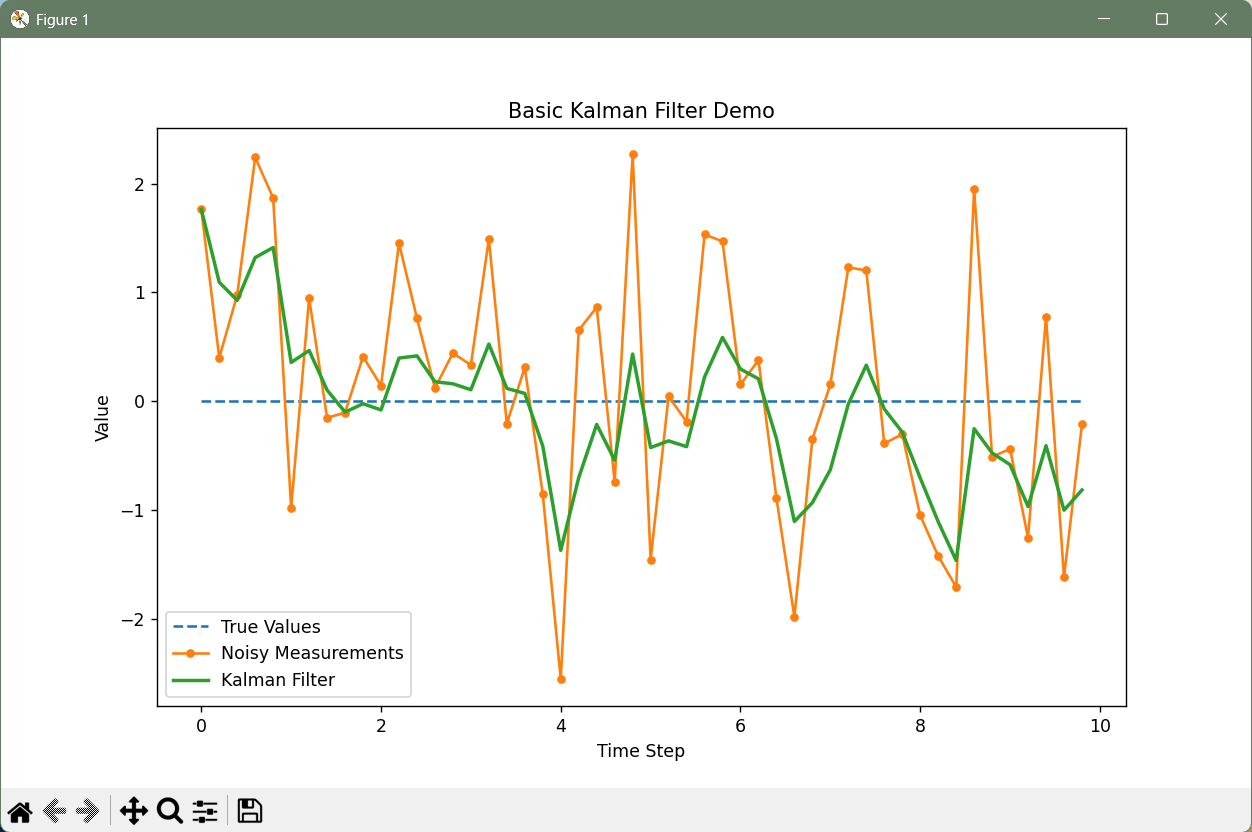 可以看到,相比于基于原始测量值估计出来的结果,卡尔曼滤波估计的结果误差平均降低了约0.36。
可以看到,相比于基于原始测量值估计出来的结果,卡尔曼滤波估计的结果误差平均降低了约0.36。
4.2 温度测量
4.2.1 问题描述
这里还以前面的例子进行说明。我们需要测量火箭发动机内部的温度,但因为温度太高无法直接测量,只能间接测量外部温度。现在需要基于观测预测对应时刻最优的内部温度。本示例中,观测量和状态量不同,但数量相等,两者间有对应关系。
4.2.2 问题建模
问题建模可以从前面几个问题开始:
观测量是什么:火箭发动机外部温度\(T_{e}\),观测向量\(\mathbf{z} = [T_{e}]\)。
希望估计的量是什么:火箭发动机内部温度\(T_{i}\)的最优估计,状态向量\(\mathbf{x} = [T_{i}]\)。
状态间存在什么关联:火箭平稳飞行时发动机内部温度基本保持不变,所以\(t\)时刻的外部温度\(T_{e}^{t}\)和\(t-1\)时刻的外部温度\(T_{e}^{t-1}\)相等,有\(T_{e}^{t} = 1 \cdot T_{e}^{t-1}\),这里的系数即为状态转移矩阵\(\mathbf{F}\)。
系统状态是否有外部因素控制:假设油门和温度的关系是每增加1油门,温度升高100度。控制输入向量\(\mathbf{u}\)即为油门,其对应的控制输入矩阵\(\mathbf{B} = [100]\)。
状态和观测之间存在什么关联:假设发动机外部温度\(T_{e}\)与内部温度\(T_{i}\)存在\(T_{e} = 0.5 \cdot T_{i}\)关系,这里的系数即为观测矩阵\(\mathbf{H}\)。
实际观测量的误差怎么样:假设发动机外部传感器的温度测量方差为0.5,那么测量噪声协方差矩阵为\(\mathbf{R} = [0.5]\)。
运行过程外部干扰怎么样:火箭发动机运行过程中剧烈振动等因素可能导致外部温度传感器松动造成测量结果不准,假设导致一个方差为0.1的误差,那么过程噪声协方差矩阵\(\mathbf{Q} = [0.1]\)。
初始预测状态怎么样:假设外部温度\(T_{e}\)的第一个观测数值\(\mathbf{z}\)为102度,根据观测矩阵\(\mathbf{H}\)的关系,可以得到第一个初始预测状态\(\mathbf{x}\)为204。对应状态协方差矩阵可设置一个较大的值,例如\(\mathbf{P} = [1]\)。
基于以上答案,便可构建基本变量和卡尔曼滤波核心步骤:
- 状态转移矩阵\(\mathbf{F} = [1]\)
- 观测矩阵\(\mathbf{H} = [0.5]\)
- 控制输入矩阵\(\mathbf{B} = [100]\)
- 过程噪声协方差矩阵\(\mathbf{Q} = [0.1]\)
- 测量噪声协方差矩阵\(\mathbf{R} = [0.5]\)
- 初始状态估计向量\(\mathbf{x} = [204]\)
- 初始状态协方差矩阵\(\mathbf{P} = [1]\)
- 输入:控制输入向量\(\mathbf{u}\)
- 输入:实际观测向量\(\mathbf{z}\)
- 输出:当前最优估计状态向量\(\mathbf{x}\)
- 输出:当前状态对应的状态协方差矩阵\(\mathbf{P}\)
4.2.3 代码实现
基于上面给出的公式和确定的参数,最终,可以通过以下代码实现卡尔曼滤波。
import numpy as np
# 给定参数
H = 0.5 # 观测矩阵
F = 1.0 # 状态转移矩阵
B = 100.0 # 控制输入矩阵
Q = 0.1 # 过程噪声协方差矩阵
R = 0.5 # 测量噪声协方差矩阵
# 指定理论值,方便评估精度,实际无法获得
ideal_value = np.zeros(12) + 200
# 系列观测与控制输入
z = [102, 104, 98, 99.7, 102, 101.5, 100.4, 101.6, 103.8, 97, 102.1, 99.3]
u = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
# 给状态赋初值
prev_state = z[0] / H
prev_error = 1.0
# 用于存放估计的状态
predict_states = []
measure_states = []
# 开始卡尔曼滤波
for i in range(len(z)):
# 预测 - 状态
predict_state = F * prev_state + B * u[i]
# 预测 - 误差
predict_error = F * prev_error * F + Q
# 更新 - 卡尔曼增益
kalman_gain = (predict_error * H) / (H * predict_error * H + R)
# 更新 - 状态
update_state = predict_state + kalman_gain * (z[i] - H * predict_state)
# 更新 - 误差
update_error = (1 - kalman_gain * H) * predict_error
# 变量赋值开启下次迭代
prev_state = update_state
prev_error = update_error
# 将预测状态保存起来
predict_states.append(update_state)
measure_states.append(z[i] / H)
# 精度评价
measure_errors = np.abs(measure_states - ideal_value)
predict_errors = np.abs(predict_states - ideal_value)
for i in range(len(predict_errors)):
print(i+1, "/", len(predict_errors), "predict error:", round(predict_errors[i], 5), "measure error:", round(measure_errors[i], 5))
print("mean measure", round(np.mean(measure_errors), 5))
print("mean predict", round(np.mean(predict_errors), 5))
运行后效果如下:
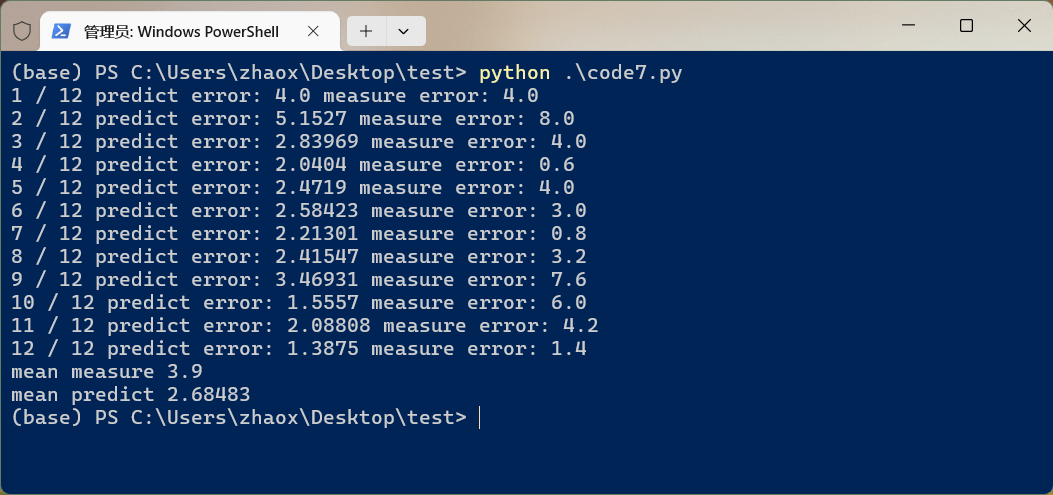 可以看到,相比于基于原始测量值估计出来的结果,卡尔曼滤波估计的结果误差平均降低了约1.22。
可以看到,相比于基于原始测量值估计出来的结果,卡尔曼滤波估计的结果误差平均降低了约1.22。
4.3 GPS二维位置估计
4.3.1 问题描述
对一个路面上行驶的车辆进行GPS位置观测\((x, y)\),因为GPS信号不佳原因导致位置观测有较大噪声。现在需要根据观测结果估计最优的位置\((x, y)\)和速度信息\((v_x, v_y)\)。在短时间内,认为车辆为匀速运动。假设车上分别有控制x方向和y方向的两个油门,每增加1油门,速度提升10。在本示例中,观测量和状态量不同,且个数不等。
4.3.2 问题建模
问题建模可以从前面几个问题开始:
观测量是什么:车辆的\(x\)、\(y\)坐标,观测向量\(\mathbf{z} = [x, y]^{T}\)。
希望估计的量是什么: 车辆真实的\(x\)、\(y\)坐标,状态向量\(\mathbf{x} = [x, y, v_x, v_y]^{T}\)。
状态间存在什么关联:基于定义的状态向量,由于认为是匀速运动,因此\(t\)时刻和\(t-1\)时刻的\(v_x\)、\(v_y\)相等,而x和y则根据公式计算\(x_t = x_{t-1} + v_x \cdot \Delta t\)、\(y_t = y_{t-1} + v_y \cdot \Delta t\),其中\(\Delta t = T_{t} - T_{t-1}\)。写成矩阵形式如下:
\[\begin{bmatrix} x_t \\ y_t \\ v_x \\ v_y \end{bmatrix} = \begin{bmatrix} 1 & 0 & \Delta t & 0\\ 0 & 1 & 0 & \Delta t\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_{t-1} \\ y_{t-1} \\ v_{x} \\ v_{y} \end{bmatrix}\]这里的系数矩阵即为状态转移矩阵\(\mathbf{F}\)。
系统状态是否有外部因素控制:有x、y两个油门,所以控制输入向量\(\mathbf{u} = [f_{x}, f_{y}]^{T}\)即为油门。每增加1油门,速度提升10,其对应的控制输入矩阵\(\mathbf{B} = \begin{bmatrix} 0 & 0\\ 0 & 0\\ 10 & 0\\ 0 & 10 \end{bmatrix}\)。
状态和观测之间存在什么关联:根据设定的观测向量和状态向量,很容易得到观测矩阵\(\mathbf{H} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{bmatrix}\)。
实际观测量的误差怎么样:假设x、y两个观测量的方差分别为5、7,协方差为0.3,那么测量噪声协方差矩阵为\(\mathbf{R} = \begin{bmatrix} 5 & 0.3\\ 0.3 & 7 \end{bmatrix}\)。
运行过程外部干扰怎么样:由于车辆行驶过程中可能出现剧烈震动等因素,导致GPS传感器测量结果不准,假设分别导致x、y方向分别出现0.05和0.03的方差,协方差为0.02,速度方差分别是0.9、0.8。由于状态向量为\(x, y, v_x, v_y\),因此过程噪声协方差矩阵大小为4×4,\(\mathbf{Q} = \begin{bmatrix} 0.05 & 0.02 & 0 & 0\\ 0.02 & 0.03 & 0 & 0\\ 0 & 0 & 0.9 & 0\\ 0 & 0 & 0 & 0.8 \end{bmatrix}\)。
初始预测状态怎么样:假设初始GPS位置观测为\(\mathbf{z} = [1, 1]^{T}\),假设第一个初始预测状态\(\mathbf{x} = [1, 1, 1, 1]^{T}\)。对应状态协方差矩阵可设置一个较大的值,例如\(\mathbf{P} = \begin{bmatrix} 100 & 0 & 0 & 0\\ 0 & 100 & 0 & 0\\ 0 & 0 & 100 & 0\\ 0 & 0 & 0 & 100 \end{bmatrix}\)。
4.3.3 代码实现
基于上面给出的公式和确定的参数,最终,可以通过以下代码实现卡尔曼滤波。
import numpy as np
from matplotlib import pyplot as plt
# 给定参数
# 两个状态间的时间间隔
delta_t = 1
# 观测矩阵
H = np.array([[1, 0, 0, 0],
[0, 1, 0, 0]])
# 状态转移矩阵
F = np.array([[1, 0, delta_t, 0],
[0, 1, 0, delta_t],
[0, 0, 1, 0],
[0, 0, 0, 1]])
# 控制输入矩阵
B = np.array([[0, 0],
[0, 0],
[10, 0],
[0, 10]])
# 过程噪声协方差矩阵
Q = np.array([[0.05, 0.02, 0, 0],
[0.02, 0.03, 0, 0],
[0, 0, 0.9, 0],
[0, 0, 0, 0.8]])
# 测量噪声协方差矩阵
R = np.array([[5.0, 0.3],
[0.3, 7.0]])
# 构造理论值,方便评估精度,实际无法获得
t = np.linspace(0, 10, 400)
x = t
y = 10 * np.sin(t)
ideal_values = np.column_stack((x, y))
ideal_vxs = []
ideal_vys = []
ideal_vxs.append(0)
ideal_vys.append(0)
for i in range(1, len(ideal_values)):
vx = np.abs(ideal_values[i][0] - ideal_values[i-1][0])
vy = np.abs(ideal_values[i][1] - ideal_values[i-1][1])
ideal_vxs.append(vx)
ideal_vys.append(vy)
# 系列观测与控制输入
z = ideal_values + np.random.normal(0, 0.1, ideal_values.shape)
u = np.zeros_like(ideal_values)
measure_vxs = np.abs(ideal_vxs + np.random.normal(0, 0.1, len(ideal_vxs)))
measure_vys = np.abs(ideal_vys + np.random.normal(0, 0.1, len(ideal_vys)))
# 给状态赋初值
prev_state = np.array([1, 1, 1, 1])
prev_error = np.array([[100, 0, 0, 0],
[0, 100, 0, 0],
[0, 0, 100, 0],
[0, 0, 0, 100]])
# 用于存放估计的状态
predict_states = []
predict_xs = []
predict_ys = []
# 开始卡尔曼滤波
for i in range(len(z)):
# 预测 - 状态
predict_state = F @ prev_state + B @ u[i]
# 预测 - 误差
predict_error = F @ prev_error @ F.T + Q
# 更新 - 卡尔曼增益
kalman_gain = predict_error @ H.T @ np.linalg.inv(H @ predict_error @ H.T + R)
# 更新 - 状态
update_state = predict_state + kalman_gain @ (z[i] - H @ predict_state)
# 更新 - 误差
update_error = (np.eye(4) - kalman_gain @ H) @ predict_error
# 变量赋值开启下次迭代
prev_state = update_state
prev_error = update_error
# 将预测状态保存起来
predict_states.append(update_state)
predict_xs.append(update_state[0])
predict_ys.append(update_state[1])
# 精度评价
predict_pos_errors = []
predict_vel_errors = []
measure_pos_errors = []
measure_vel_errors = []
for i in range(len(predict_states)):
cur_state = predict_states[i]
dx = np.abs(cur_state[0] - ideal_values[i][0])
dy = np.abs(cur_state[1] - ideal_values[i][1])
predict_pos_errors.append(np.sqrt(dx**2 + dy**2))
dvx = np.abs(np.abs(cur_state[2]) - ideal_vxs[i])
dvy = np.abs(np.abs(cur_state[3]) - ideal_vys[i])
predict_vel_errors.append(np.sqrt(dvx**2 + dvy**2))
dx = np.abs(z[i][0] - ideal_values[i][0])
dy = np.abs(z[i][1] - ideal_values[i][1])
measure_pos_errors.append(np.sqrt(dx**2 + dy**2))
dvx = np.abs(measure_vxs[i] - ideal_vxs[i])
dvy = np.abs(measure_vxs[i] - ideal_vys[i])
measure_vel_errors.append(np.sqrt(dvx**2 + dvy**2))
print("mean measure pos:", round(np.mean(measure_pos_errors), 5))
print("mean predict pos:", round(np.mean(predict_pos_errors), 5))
print("mean measure vel:", round(np.mean(measure_vel_errors), 5))
print("mean predict vel:", round(np.mean(predict_vel_errors), 5))
# 可视化
plt.figure(figsize=(10, 6))
plt.plot(ideal_values[:,0], ideal_values[:,1], 'g-', label='ground truth')
plt.plot(z[:,0], z[:,1], 'r-', label='GPS Measure')
plt.plot(predict_xs, predict_ys, 'b-', label='Predict')
plt.legend()
plt.title('GPS Traj.')
plt.xlabel('X (m)')
plt.ylabel('Y (m)')
plt.grid(True)
plt.show()
运行后效果如下。
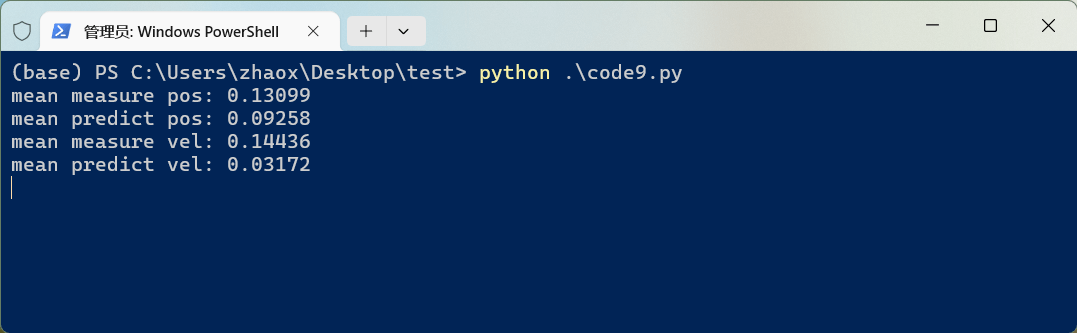
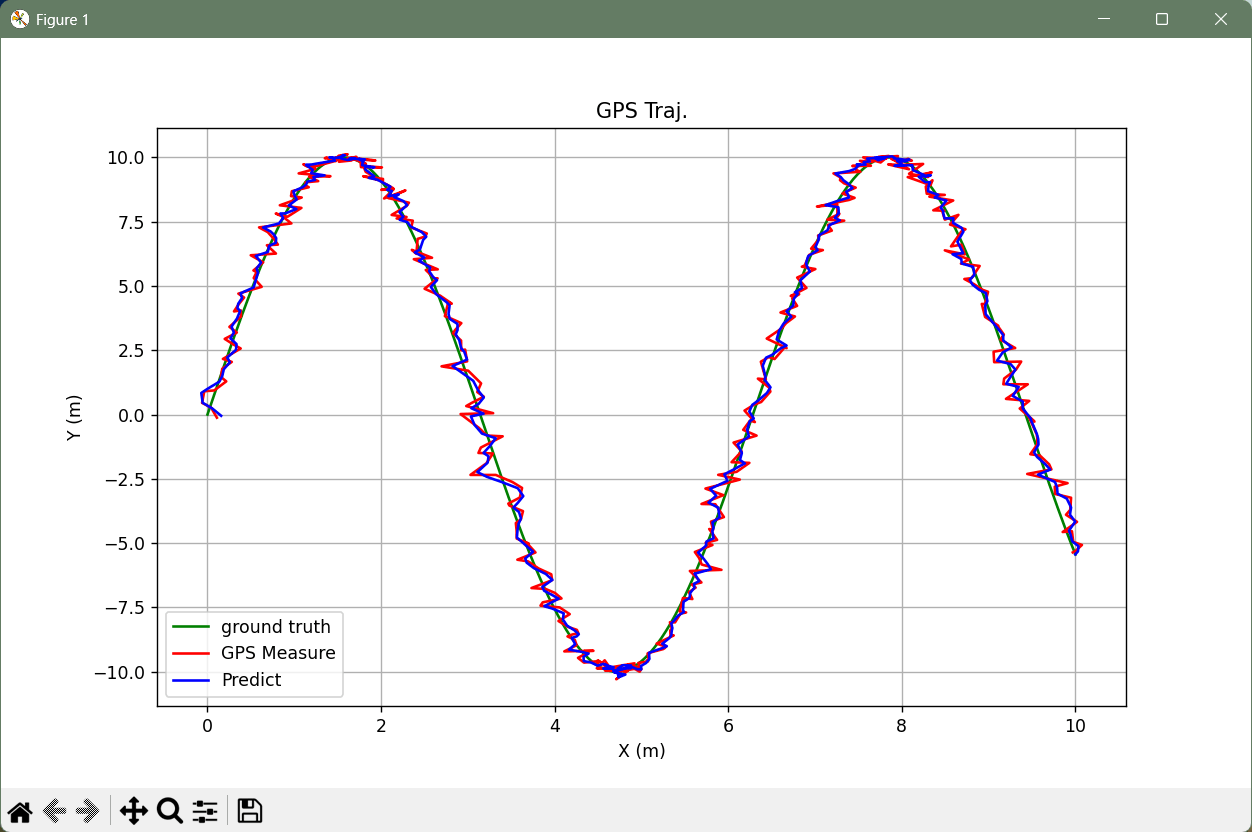 相比于原始数据计算出的状态,卡尔曼滤波得到的位置和速度对应的误差均有下降。
相比于原始数据计算出的状态,卡尔曼滤波得到的位置和速度对应的误差均有下降。
4.4 多个温度传感器融合
4.4.1 问题描述
在前面的例子中,我们主要介绍的都是感兴趣的量无法直接观测,通过间接观测其它相关量从而推测它的值(即使观测量和预测量相同也可以将其当作无法直接观测处理),对应卡尔曼滤波适合的第一种情况。现实中还有另一种情况,就是我们可能使用多个传感器对某个变量同时进行观测,需要基于多个观测量给出感兴趣量的最优估计。
还是从简单到复杂,首先从4.2的温度测量开始。为了进一步提高估计精度,我们在火箭发动机的四周分别安装了4个温度传感器。现在需要基于4个外部观测预测对应时刻最优的内部温度。
4.4.2 问题建模
问题建模可以从前面几个问题开始:
观测量是什么:4个火箭发动机外部温度\(T_{e}\),观测向量\(\mathbf{z} = [T_{e}^{1}, T_{e}^{2}, T_{e}^{3}, T_{e}^{4}]\)。
希望估计的量是什么:火箭发动机内部温度\(T_{i}\)的最优估计,状态向量\(\mathbf{x} = [T_{i}]\)。
状态间存在什么关联:火箭平稳飞行时发动机内部温度基本保持不变,所以\(t\)时刻的外部温度\(T_{e}^{t}\)和\(t-1\)时刻的外部温度\(T_{e}^{t-1}\)相等,有\(T_{e}^{t} = 1 \cdot T_{e}^{t-1}\),这里的系数即为状态转移矩阵\(\mathbf{F}\)。
系统状态是否有外部因素控制:假设油门和温度的关系是每增加1油门,温度升高100度。控制输入向量\(\mathbf{u}\)即为油门,其对应的控制输入矩阵\(\mathbf{B} = [100]\)。
状态和观测之间存在什么关联:假设发动机外部温度\(T_{e}\)与内部温度\(T_{i}\)存在\(T_{e} = 0.5 \cdot T_{i}\)关系,这里的系数即为观测矩阵\(\mathbf{H} = \begin{bmatrix} 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \end{bmatrix}\)。
实际观测量的误差怎么样:假设发动机外部传感器的温度测量精度稍有差异、彼此独立观测,那么测量噪声协方差矩阵为\(\mathbf{R} = \begin{bmatrix} 0.5 & 0 & 0 & 0\\ 0 & 0.6 & 0 & 0\\ 0 & 0 & 0.4 & 0\\ 0 & 0 & 0 & 0.3 \end{bmatrix}\)。
运行过程外部干扰怎么样:火箭发动机运行过程中剧烈振动等因素可能导致外部温度传感器松动造成测量结果不准,假设导致一个方差为0.1的误差,那么过程噪声协方差矩阵\(\mathbf{Q} = [0.1]\)。
初始预测状态怎么样:假设外部温度\(T_{e}\)的第一个观测\(\mathbf{z}\)分别为102、103、101、100.5度,可以得到第一个初始预测状态\(\mathbf{x}\)为204。对应状态协方差矩阵可设置一个较大的值,例如\(\mathbf{P} = [1]\)。
基于以上答案,便可构建基本变量和卡尔曼滤波核心步骤:
- 状态转移矩阵\(\mathbf{F} = [1]\)
- 观测矩阵\(\mathbf{H} = \begin{bmatrix} 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \end{bmatrix}\)
- 控制输入矩阵\(\mathbf{B} = [100]\)
- 过程噪声协方差矩阵\(\mathbf{Q} = [0.1]\)
- 测量噪声协方差矩阵\(\mathbf{R} = \begin{bmatrix} 0.5 & 0 & 0 & 0\\ 0 & 0.6 & 0 & 0\\ 0 & 0 & 0.4 & 0\\ 0 & 0 & 0 & 0.3 \end{bmatrix}\)
- 初始状态估计向量\(\mathbf{x} = [102, 103, 101, 100.5]\)
- 初始状态协方差矩阵\(\mathbf{P} = [1]\)
- 输入:控制输入向量\(\mathbf{u}\)
- 输入:实际观测向量\(\mathbf{z}\)
- 输出:当前最优估计状态向量\(\mathbf{x}\)
- 输出:当前状态对应的状态协方差矩阵\(\mathbf{P}\)
4.4.3 代码实现
基于上面给出的公式和确定的参数,最终,可以通过以下代码实现卡尔曼滤波。
import numpy as np
# 给定参数
# 观测矩阵
H = np.array([[0.5],
[0.5],
[0.5],
[0.5]])
# 状态转移矩阵
F = np.array([[1.0]])
# 控制输入矩阵
B = np.array([[100.0]])
# 过程噪声协方差矩阵
Q = np.array([[0.1]])
# 测量噪声协方差矩阵
R = np.array([[0.5, 0, 0, 0],
[0, 0.6, 0, 0],
[0, 0, 0.4, 0],
[0, 0, 0, 0.3]])
# 指定理论值,方便评估精度,实际无法获得
ideal_value = np.zeros(12) + 200
# 系列观测与控制输入
z = np.array([[102, 103, 101, 100.5],
[104, 110, 103, 102],
[98, 109, 104, 107],
[99.7, 95, 99, 104],
[102, 110, 98, 102],
[101.5, 103, 105, 96],
[100.4, 102, 103, 103],
[101.6, 110, 104, 107],
[103.8, 94, 98, 99],
[97, 102, 99, 101],
[102.1, 102, 99, 104],
[99.3, 108, 102, 103]])
u = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
# 给状态赋初值
prev_state = np.array([[204]])
prev_error = np.array([[1.0]])
# 用于存放估计的状态
predict_states = []
measure_states = []
# 开始卡尔曼滤波
for i in range(len(z)):
# # 预测 - 状态
predict_state = F @ prev_state + B @ np.array([[u[i]]])
# # 预测 - 误差
predict_error = F @ prev_error @ F.T + Q
# 更新 - 卡尔曼增益
kalman_gain = predict_error @ H.T @ np.linalg.inv(H @ predict_error @ H.T + R)
# 更新 - 状态
update_state = predict_state + kalman_gain @ (np.array([z[i]]).T - H @ predict_state)
# 更新 - 误差
update_error = (np.eye(1) - kalman_gain @ H) @ predict_error
# 变量赋值开启下次迭代
prev_state = update_state
prev_error = update_error
# 将预测状态保存起来
predict_states.append(update_state[0][0])
measure_states.append(np.mean(z[i] * 2))
# 精度评价
measure_errors = np.abs(measure_states - ideal_value)
predict_errors = np.abs(predict_states - ideal_value)
for i in range(len(predict_errors)):
print(i+1, "/", len(predict_errors), "predict error:", round(predict_errors[i], 5), "measure error:", round(measure_errors[i], 5))
print("mean measure", round(np.mean(measure_errors), 5))
print("mean predict", round(np.mean(predict_errors), 5))
运行后效果如下:
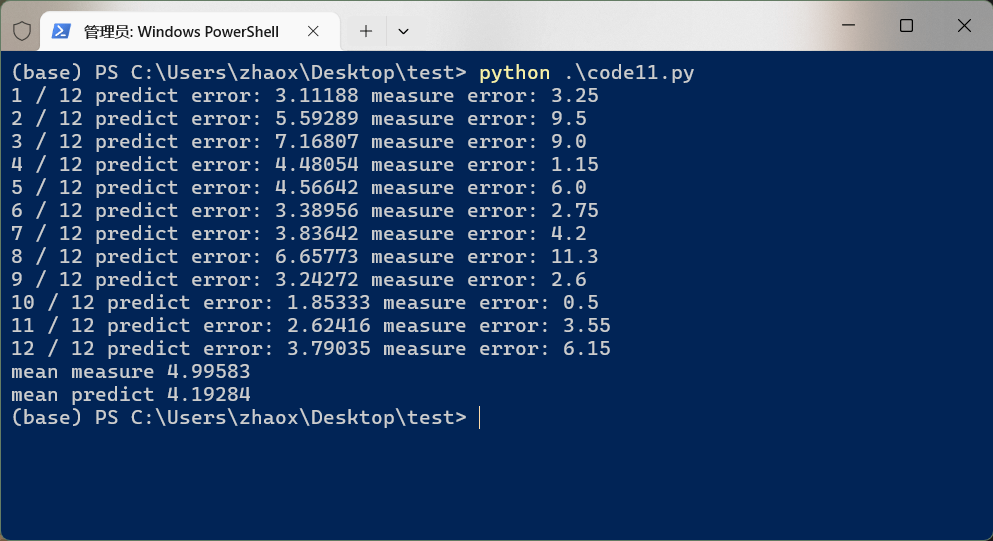 可以看到,相比于基于原始测量值估计出来的结果,卡尔曼滤波估计的结果误差平均降低了约0.8。
可以看到,相比于基于原始测量值估计出来的结果,卡尔曼滤波估计的结果误差平均降低了约0.8。
4.5 LiDAR-GPS传感器融合
4.5.1 问题描述
进一步研究多传感器融合问题。对于多传感器融合,本质上就是将多个观测矩阵和测量协方差矩阵融合到一起,其余步骤与之前相同。
对于一个机器人,携带了LiDAR和GPS两个传感器同时观测机器人的位置。现在需要融合两者的观测,给出最优的位置和速度估计。这里假设观测数据已经经过预处理,包括:(1)LiDAR和GPS观测观测频率相同;(2)LiDAR和GPS的位置观测已经转换到同一坐标系。认为在短时间内,机器人为匀速运动。
4.5.2 问题建模
问题建模可以从前面几个问题开始:
观测量是什么:LiDAR的X、Y观测,GPS的X、Y观测,观测向量\(\mathbf{z} = [x_{L}, y_{L}, x_{G}, y_{G}]\)。
希望估计的量是什么:机器人在某个时刻的最优位置和速度,状态向量\(\mathbf{x} = [x, y, v_{x}, v_{y}]\)。
状态间存在什么关联:基于定义的状态向量,由于认为是匀速运动,因此\(t\)时刻和\(t-1\)时刻的\(v_x\)、\(v_y\)相等,而x和y则根据公式计算\(x_t = x_{t-1} + v_x \cdot \Delta t\)、\(y_t = y_{t-1} + v_y \cdot \Delta t\),其中\(\Delta t = T_{t} - T_{t-1}\)。写成矩阵形式如下:
\[\begin{bmatrix} x_t \\ y_t \\ v_x \\ v_y \end{bmatrix} = \begin{bmatrix} 1 & 0 & \Delta t & 0\\ 0 & 1 & 0 & \Delta t\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_{t-1} \\ y_{t-1} \\ v_{x} \\ v_{y} \end{bmatrix}\]系统状态是否有外部因素控制:有x、y两个油门,所以控制输入向量\(\mathbf{u} = [f_{x}, f_{y}]^{T}\)即为油门。每增加1油门,速度提升10,其对应的控制输入矩阵\(\mathbf{B} = \begin{bmatrix} 0 & 0\\ 0 & 0\\ 10 & 0\\ 0 & 10 \end{bmatrix}\)。
状态和观测之间存在什么关联:根据设定的观测向量和状态向量,按照z=Hx,很容易得到融合LiDAR和GPS的观测矩阵\(\mathbf{H} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{bmatrix}\)。
实际观测量的误差怎么样:假设LiDAR的X、Y两个观测量的方差分别为5、7,协方差为0.3,GPS的X、Y方差分别为10、9,协方差为1。两个传感器互相独立。按照\(x_{L}, y_{L}, x_{G}, y_{G}\)顺序,那么测量噪声协方差矩阵为\(\mathbf{R} = \begin{bmatrix} 5 & 0.3 & 0 & 0\\ 0.3 & 7 & 0 & 0\\ 0 & 0 & 10 & 1\\ 0 & 0 & 1 & 9 \end{bmatrix}\)。
运行过程外部干扰怎么样:由于车辆行驶过程中可能出现剧烈震动等因素,导致传感器测量结果不准,假设分别导致x、y方向分别出现0.05和0.03的方差,协方差为0.02,速度方差分别是0.9、0.8。由于状态向量为\(x, y, v_x, v_y\),因此过程噪声协方差矩阵大小为4×4,\(\mathbf{Q} = \begin{bmatrix} 0.05 & 0.02 & 0 & 0\\ 0.02 & 0.03 & 0 & 0\\ 0 & 0 & 0.9 & 0\\ 0 & 0 & 0 & 0.8 \end{bmatrix}\)。
初始预测状态怎么样:假设初始观测为\(\mathbf{z} = [0.1, 0.2, 0.5, 0.4]^{T}\),假设第一个初始预测状态\(\mathbf{x} = [0.2, 0.3, 1, 1]^{T}\)。对应状态协方差矩阵可设置一个较大的值,例如\(\mathbf{P} = \begin{bmatrix} 100 & 0 & 0 & 0\\ 0 & 100 & 0 & 0\\ 0 & 0 & 100 & 0\\ 0 & 0 & 0 & 100 \end{bmatrix}\)。
4.5.3 代码实现
基于上面给出的公式和确定的参数,最终,可以通过以下代码实现卡尔曼滤波。
import numpy as np
from matplotlib import pyplot as plt
# 给定参数
# 两个状态间的时间间隔
delta_t = 1
# 观测矩阵
H = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[1, 0, 0, 0],
[0, 1, 0, 0]])
# 状态转移矩阵
F = np.array([[1, 0, delta_t, 0],
[0, 1, 0, delta_t],
[0, 0, 1, 0],
[0, 0, 0, 1]])
# 控制输入矩阵
B = np.array([[0, 0],
[0, 0],
[10, 0],
[0, 10]])
# 过程噪声协方差矩阵
Q = np.array([[0.05, 0.02, 0, 0],
[0.02, 0.03, 0, 0],
[0, 0, 0.9, 0],
[0, 0, 0, 0.8]])
# 测量噪声协方差矩阵
R = np.array([[5, 0.3, 0, 0],
[0.3, 7, 0, 0],
[0, 0, 10, 1],
[0, 0, 1, 9]])
# 构造理论值,方便评估精度,实际无法获得
t = np.linspace(0, 2*np.pi, 100)
x = 10 * np.cos(t)
y = 10 * np.sin(t)
ideal_values = np.vstack([x, y])
ideal_vxs = []
ideal_vys = []
ideal_vxs.append(0)
ideal_vys.append(0)
for i in range(1, len(ideal_values[0])):
vx = np.abs(ideal_values[0][i] - ideal_values[0][i-1])
vy = np.abs(ideal_values[1][i] - ideal_values[1][i-1])
ideal_vxs.append(vx)
ideal_vys.append(vy)
# 系列观测与控制输入
z_lidar = ideal_values + np.random.normal(0, 0.5, ideal_values.shape)
z_lidar = z_lidar.T
z_gps = ideal_values + np.random.normal(0, 1, ideal_values.shape)
z_gps = z_gps.T
u = np.zeros_like(ideal_values)
u = u.T
measure_vxs = np.abs(ideal_vxs + np.random.normal(0, 0.1, len(ideal_vxs)))
measure_vys = np.abs(ideal_vys + np.random.normal(0, 0.1, len(ideal_vys)))
# 给状态赋初值
prev_state = np.array([0.2, 0.3, 1, 1])
prev_error = np.array([[100, 0, 0, 0],
[0, 100, 0, 0],
[0, 0, 100, 0],
[0, 0, 0, 100]])
# 用于存放估计的状态
predict_states = []
predict_xs = []
predict_ys = []
# 开始卡尔曼滤波
for i in range(len(z_lidar)):
# 预测 - 状态
predict_state = F @ prev_state + B @ u[i].T
# 预测 - 误差
predict_error = F @ prev_error @ F.T + Q
# 更新 - 卡尔曼增益
kalman_gain = predict_error @ H.T @ np.linalg.inv(H @ predict_error @ H.T + R)
# 更新 - 状态
update_state = predict_state + kalman_gain @ (np.concatenate([z_lidar[i], z_gps[i]]) - H @ predict_state)
# 更新 - 误差
update_error = (np.eye(4) - kalman_gain @ H) @ predict_error
# 变量赋值开启下次迭代
prev_state = update_state
prev_error = update_error
# 将预测状态保存起来
predict_states.append(update_state)
predict_xs.append(update_state[0])
predict_ys.append(update_state[1])
# 精度评价
predict_pos_errors = []
predict_vel_errors = []
measure_pos_errors = []
measure_vel_errors = []
for i in range(len(predict_states)):
cur_state = predict_states[i]
dx = np.abs(cur_state[0] - ideal_values[0][i])
dy = np.abs(cur_state[1] - ideal_values[1][i])
predict_pos_errors.append(np.sqrt(dx**2 + dy**2))
dvx = np.abs(np.abs(cur_state[2]) - ideal_vxs[i])
dvy = np.abs(np.abs(cur_state[3]) - ideal_vys[i])
predict_vel_errors.append(np.sqrt(dvx**2 + dvy**2))
dx = np.abs((z_lidar[i][0]+z_gps[i][0])/2 - ideal_values[0][i])
dy = np.abs((z_lidar[i][1]+z_gps[i][1])/2 - ideal_values[1][i])
measure_pos_errors.append(np.sqrt(dx**2 + dy**2))
dvx = np.abs(measure_vxs[i] - ideal_vxs[i])
dvy = np.abs(measure_vxs[i] - ideal_vys[i])
measure_vel_errors.append(np.sqrt(dvx**2 + dvy**2))
print("mean measure pos:", round(np.mean(measure_pos_errors), 5))
print("mean predict pos:", round(np.mean(predict_pos_errors), 5))
print("mean measure vel:", round(np.mean(measure_vel_errors), 5))
print("mean predict vel:", round(np.mean(predict_vel_errors), 5))
# 可视化
plt.figure(figsize=(10, 6))
plt.plot(ideal_values[0,:], ideal_values[1,:], 'g-', label='Ground Truth')
plt.plot(z_gps[:,0], z_gps[:,1], 'r-', label='GPS Measure')
plt.plot(z_lidar[:,0], z_lidar[:,1], 'y-', label='LiDAR Measure')
plt.plot(predict_xs, predict_ys, 'b-', label='Predict')
plt.legend()
plt.title('GPS Traj.')
plt.xlabel('X (m)')
plt.ylabel('Y (m)')
plt.grid(True)
plt.show()
运行后效果如下。
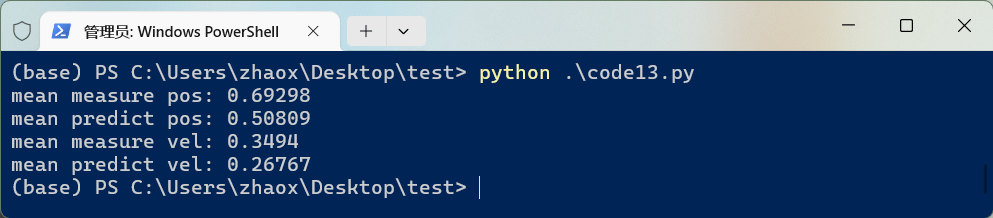
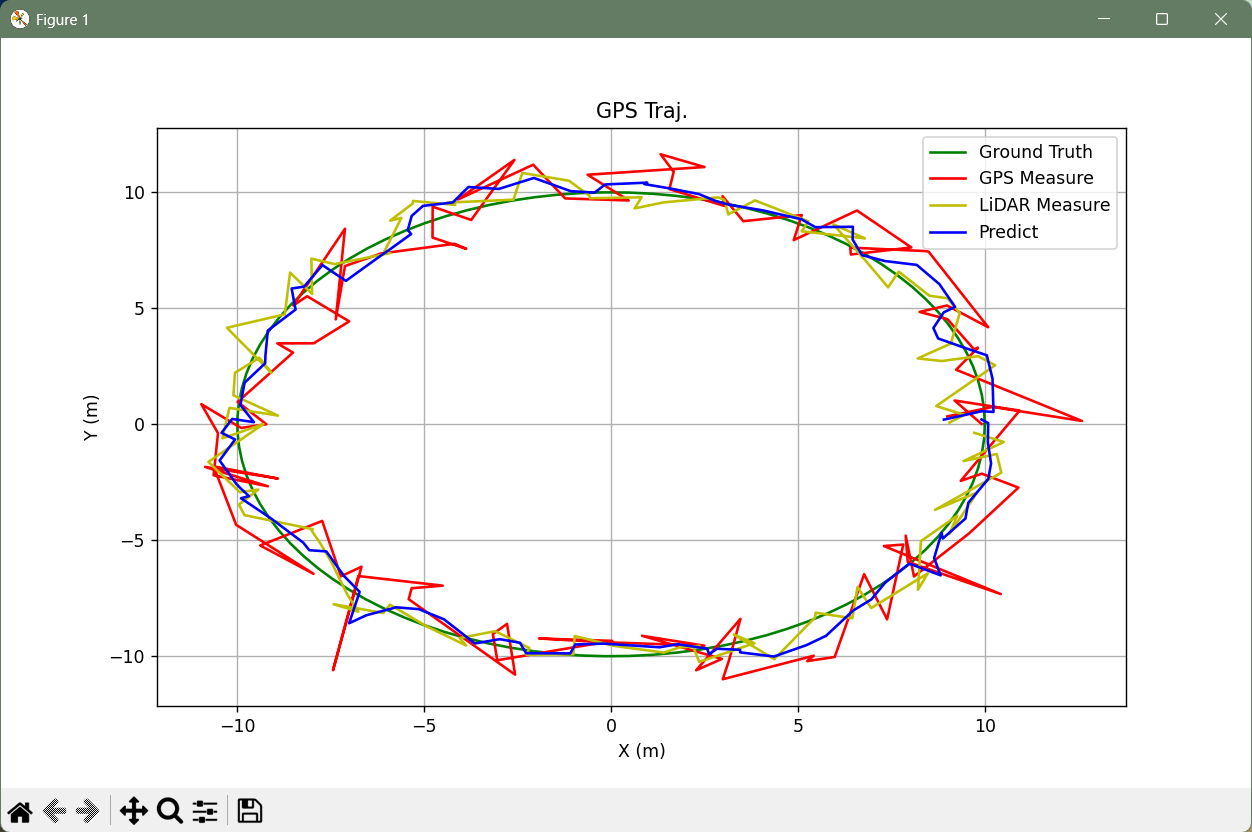 相比于原始数据通过简单平均计算出的位置和速度,卡尔曼滤波得到的位置和速度对应的误差均有下降。
相比于原始数据通过简单平均计算出的位置和速度,卡尔曼滤波得到的位置和速度对应的误差均有下降。
5.实际应用中的进一步讨论
5.1 过程噪声协方差矩阵Q
过程噪声协方差矩阵Q表征系统模型的不确定性(如未建模动态、外部干扰)。确定方法可以通过理论分析或实验标定。
- Q过大:过度信任测量值,响应快速,但输出波动大(高频噪声敏感)
- Q过小:过度信任预测模型,响应滞后,对突变不敏感(系统发散风险)
5.2 观测噪声协方差矩阵R
观测噪声协方差矩阵R反映传感器测量精度。确定方法可以从设备参数中直接获得,也可以通过传感器标定获得。
- R过大:更信任模型预测、忽略测量值,结果更平滑但可能偏离真实值
- R过小:更信任测量值,滤波结果接近原始测量
Q/R决定卡尔曼增益K的大小:
- 高Q/R比导致K增大,更信任测量值
- 低Q/R比导致K减小,更信任模型预测
5.3 状态初值
对于系统的状态初值,若有先验知识(如系统启动位置),直接赋值;若无先验信息,可用首次测量值初始化。而初始状态对应的协方差矩阵一般可以设为一个较大的数(100等),但如果过大可能引起初始震荡,如果过小会导致收敛慢,且可能陷入局部最优。
系统不同问题的潜在改善方向:
- 系统发散:可能是模型不准或Q过小,可以增大Q或改进模型
- 系统滞后:可能是Q过小,可以增大Q或减小R
- 系统震荡:可能是R过小,可以增大R
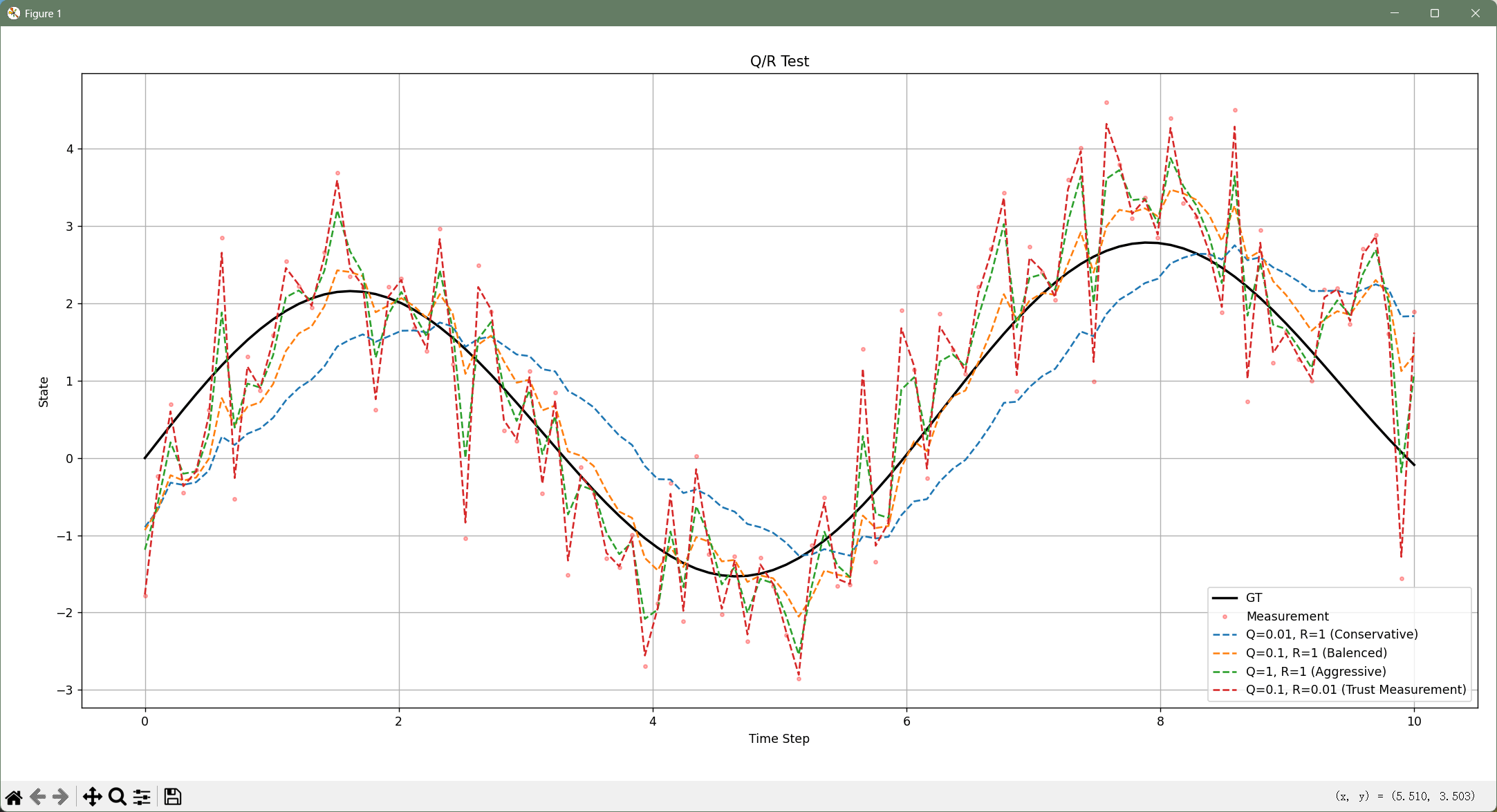
5.4 不同参数对滤波影响分析
下面的代码展示了不同的参数对滤波的影响。
import numpy as np
import matplotlib.pyplot as plt
class KalmanFilter:
def __init__(self, q, r):
self.q = q # 过程噪声方差
self.r = r # 测量噪声方差
self.x = 0 # 初始状态估计
self.p = 1 # 初始估计误差协方差
def update(self, z):
# 预测步骤
x_pred = self.x
p_pred = self.p + self.q
# 更新步骤
k = p_pred / (p_pred + self.r)
self.x = x_pred + k * (z - x_pred)
self.p = (1 - k) * p_pred
return self.x
def simulate_data(n=100):
# 生成真实轨迹(正弦波+线性趋势)
t = np.linspace(0, 10, n)
truth = 2 * np.sin(t) + 0.1 * t
# 添加测量噪声
noise = np.random.normal(0, 1, n)
return t, truth, truth + noise
def main():
t, truth, measurements = simulate_data()
# 测试不同Q/R组合
params = [
{'q': 0.01, 'r': 1, 'label': 'Q=0.01, R=1 (Conservative)'},
{'q': 0.1, 'r': 1, 'label': 'Q=0.1, R=1 (Balenced)'},
{'q': 1, 'r': 1, 'label': 'Q=1, R=1 (Aggressive)'},
{'q': 0.1, 'r': 0.01, 'label': 'Q=0.1, R=0.01 (Trust Measurement)'}
]
plt.figure(figsize=(12, 6))
plt.plot(t, truth, 'k-', linewidth=2, label='GT')
plt.plot(t, measurements, 'r.', alpha=0.3, label='Measurement')
for param in params:
kf = KalmanFilter(param['q'], param['r'])
estimates = [kf.update(z) for z in measurements]
plt.plot(t, estimates, '--', linewidth=1.5, label=param['label'])
plt.title('Q/R Test')
plt.xlabel('Time Step')
plt.ylabel('State')
plt.legend()
plt.tight_layout()
plt.grid(True)
plt.show()
if __name__ == '__main__':
main()
6.非线性情况下的扩展卡尔曼滤波
前面我们提到,经典卡尔曼滤波的假设之一就是状态以及状态和观测之间的关系都是线性的、适用于线性高斯系统,但现实中情况显然会更加复杂。如何将卡尔曼滤波应用于非线性情况是另一个重要的话题。直接来说,对于非线性系统,可以使用扩展卡尔曼滤波器,Extended Kalman Filter, EKF。
一句话概述:扩展卡尔曼滤波通过局部线性化处理实现对动态系统的高效跟踪,其核心原理是通过一阶泰勒展开近似非线性函数,并沿用卡尔曼滤波的递推框架进行状态预测与更新。这种非线性主要体现在状态转移方程、观测方程上。
6.1 EKF和KF的异同
非线性系统不能像线性系统那样写出一个全局、不变的状态转移矩阵\(F\)和观测矩阵\(H\),这就导致两个问题:
-
写不出状态转移矩阵\(\mathbf F\)就无法计算预测状态的误差。尽管可以根据模型计算得到预测结果,却没有办法进行预测误差计算。因为卡尔曼滤波中预测误差计算需要用到状态转移矩阵\(\mathbf F\),但非线性系统又写不出\(\mathbf F\)。
-
写不出观测矩阵\(\mathbf H\)就无法计算卡尔曼增益。没有卡尔曼增益进一步就无法对预测值进行修正,以及计算相应误差。
为了解决这个问题,可以考虑进行局部线性化:
-
对于非线性的状态转移:在\(\mathbf X_{t-1}\)时刻对非线性模型采用一阶泰勒展开进行线性化,这样最终能算得一个雅可比矩阵。用这个雅可比矩阵即可代替状态转移矩阵\(\mathbf F\),结合误差公式可计算预测误差。
-
对于非线性的观测方程:在\(\mathbf X_t\)时刻对非线性模型采用一阶泰勒展开进行线性化,这样最终能算得一个雅可比矩阵。用这个雅可比矩阵即可代替观测矩阵\(\mathbf H\),结合公式即可修正估计和计算误差。
因此,所以对于非线性系统,使用扩展卡尔曼滤波应该包含以下几个步骤:
-
- 根据非线性状态转移模型和上一个状态,计算当前状态预测值
-
- 对非线性状态转移模型在\(X_{t-1}\)处线性化,求解雅可比矩阵\(\mathbf F\)
-
- 基于解算的雅可比矩阵\(\mathbf F\)和给定误差,计算当前预测状态对应的误差
-
- 对非线性观测模型在\(X_t\)处线性化,求解雅可比矩阵\(\mathbf H\)
-
- 根据上一状态预测误差、给定的观测误差和解算的雅可比矩阵\(\mathbf H\),计算卡尔曼增益
-
- 根据当前预测状态、实际观测和雅可比矩阵\(\mathbf H\),结合卡尔曼增益平衡预测与观测权重,修正状态预测
-
- 根据计算得到的卡尔曼增益、上一个状态预测误差、雅可比矩阵\(\mathbf H\),计算修正后状态对应的误差
不断重复以上步骤即可实现卡尔曼滤波。可以看到,相比于标准KF,主要是增加了第2步和第4步,用于解算状态转移矩阵\(\mathbf F\)和观测矩阵\(\mathbf H\)。这也说明了为什么EKF相比于KF计算量会大。因为每次计算都要在新的位置重新线性化,计算对应的雅可比矩阵。尽管计算F、H的公式可以事前推导完成,但在运行中仍然需要基于该公式重新计算。而在标准KF中,\(\mathbf F\)、\(\mathbf H\)都是常量固定的。当然,在实际使用中,状态转移和测量并非都是非线性,可能某一个为非线性。
最后回答一个问题:为什么非线性系统写不出全局的状态转移矩阵和观测矩阵?主要有以下两方面原因:
- 输入与输出不成比例:非线性系统的状态转移/观测函数不满足叠加原理(\(f(ax_{1}+bx_{2})\ne af(x_{1})+bf(x_{2})\)),而全局状态转移矩阵\(\mathbf F\)/观测矩阵\(\mathbf H\)则要求状态变换严格遵循线性叠加。
- 变量间耦合复杂:变量间存在多项式或超越函数(指数、对数、三角函数、反三角函数等)关系,无法通过常数的状态转移矩阵\(\mathbf F\)/观测矩阵\(\mathbf H\)统一描述所有状态/观测的转移规律。
具体来说,比如观测函数中包含三角函数,无法直接写出常量的观测矩阵\(\mathbf H\)。或者状态由多个变量决定。例如t时刻有状态\([A_t, B_t, C_t]\)、t-1时刻有状态\([A_{t-1}, B_{t-1}, C_{t-1}]\)。但\(A_{t}\)并非只由\(A_{t-1}\)决定,可能由\(A_{t-1}\)、\(B_{t-1}\)、\(C_{t-1}\)共同决定。这种情况同样无法写出常量状态转移矩阵,也属于典型非线性场景。
6.2 基础知识
在正式介绍如何对非线性模型进行线性化前,需要先介绍一些基础知识。
6.2.1 泰勒展开
简单回顾一下泰勒展开。EKF主要用到一阶泰勒展开。一阶泰勒展开是用于在某个点附近用线性函数近似表示原函数的数学方法。对于某个函数\(f(x)\),在\(x_{0}\)处进行泰勒展开,公式如下:
\[f(x) \approx f(x_{0}) + f'(x_{0})(x-x_{0})\]其中,\(f'(x_{0})\)表示原函数\(f(x)\)在\(x_{0}\)处的导数。一阶泰勒展开在几何上表示函数在\(x_{0}\)处的切线,通过切线近似原函数。例如,对\(f(x) = sinx\)在\(x_{0}=0\)处展开,有:
\[sinx \approx sin(0) + cos(0)\cdot (x-0) = x\]6.2.2 求函数的偏导数
在高数中我们学习过求函数的导数。但如果函数有多个自变量,那么我们就可以对其中某个自变量求偏导数,从而反映函数在特定方向上的变化率。求偏导的一个核心原则是对求导的变量按求导法则求导,非求导变量看做常量。
例如,我们有函数\(f(x,y,z) = 3x^{2}+2xy^{2}+6yz+8z+9\),分别对x、y、z自变量求导有:
\[\left\{\begin{matrix} \frac{\partial f(x,y,z)}{\partial x} = 6x +2y^{2} \\ \frac{\partial f(x,y,z)}{\partial y} = 4x+6z \\ \frac{\partial f(x,y,z)}{\partial z} = 6y+8 \end{matrix}\right.\]这样,便完成了对函数各自变量偏导数的求解。
6.2.3 向量/矩阵函数求导
在实际中可能会碰到一种函数,这个函数的自变量或因变量不再是标量,而是向量甚至矩阵,这时如何对这个函数求导呢?给出一个向量函数的例子,例如自变量\(\mathbf{x} = [x, y, z]\),函数为\(\mathbf f(\mathbf{x})= \begin{bmatrix} x^{2}y +z \\ 3y+x+z \end{bmatrix}\)。这个函数的输入和输出都是一个二维向量。例如,输入\(\mathbf{x}=[1, 1, 1]\),输出为\([2, 5]\)。
首先介绍输入是向量、输出是标量函数的情况,对于某个函数\(f(\mathbf{x})\),其自变量\(\mathbf{x} = [x_{1}, x_{2}, x_{3}, \dots, x_{n}]^{T}\)包含\(n\)个分量。我们可以分别对各分量求偏导,从而得到一个偏导数向量\([\frac{\partial f}{\partial x_{0}}, \frac{\partial f}{\partial x_{1}}, \frac{\partial f}{\partial x_{2}},\dots,\frac{\partial f}{\partial x_{n}}]^{T}\)。那么,这个偏导数向量就可以看做是该函数对于自变量的导数。
进一步,如果某个函数\(\mathbf f(\mathbf{x})\)输入是一个\(n\)维向量,输出是一个\(m\)维向量,如下所示:
\[\mathbf{y} = f(\mathbf{x}) = \begin{bmatrix} f_{1}(x_{1}, x_{2}, \dots, x_{n}) \\ f_{2}(x_{1}, x_{2}, \dots, x_{n}) \\ \dots \\ f_{m}(x_{1}, x_{2}, \dots, x_{n}) \end{bmatrix}\]如何求函数的导数呢?对于单个函数,我们按照上面说的,分别对\(n\)个自变量求偏导,得到该函数关于自变量\(\mathbf{x}\)的导数向量。对于多个函数,重复上述步骤,对\(f_{1},f_{2},\dots,f_{m}\)求导,得到\(f_{1}\)关于\(\mathbf{x}\)的导数向量、\(f_{2}\)关于\(\mathbf{x}\)的导数向量…而这些导数向量合在一起,则是整个\(\mathbf f(\mathbf{x})\)关于\(\mathbf{x}\)的导数。最终,我们可以得到如下矩阵:
\[\mathbf J = \frac{\partial \mathbf f}{\partial \mathbf x} = \begin{bmatrix} \frac{\partial f_{1}}{\partial x_{1}} & \dots & \frac{\partial f_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}} & \dots & \frac{\partial f_{m}}{\partial x_{n}} \end{bmatrix}\]这个矩阵也就表示了整个\(\mathbf f(\mathbf{x})\)关于\(\mathbf{x}\)的导数,其维度为m×n,我们将其称为雅可比矩阵(Jacobian Matrix)。因此,对向量/矩阵函数求导就等于是求雅可比矩阵。
6.3 非线性模型局部线性化
有了上面的知识就更容易理解EKF中的线性化。核心就是对非线性函数在指定位置进行一阶泰勒展开(6.1部分),由于泰勒展开中包含函数的导数,所以需要对向量函数求导,也就是求对应的雅可比矩阵(6.3部分)。因此,对于一个\(n\)维的向量\(\mathbf x\),\(\mathbf f(\mathbf x)\)是\(m\)维向量函数时,对其在\(\mathbf a\)处一阶泰勒展开有:
\[\mathbf f(\mathbf x) \approx \mathbf f(\mathbf a)+\mathbf f'(\mathbf a)(\mathbf x - \mathbf a)\]根据向量函数求导方法,自然有:
\[\mathbf f(\mathbf x) \approx \mathbf f(\mathbf a)+\mathbf J_{\mathbf f} (\mathbf a)(\mathbf x - \mathbf a)\]其中最核心的也就是求解\(\mathbf f(\mathbf x)\)在\(\mathbf a\)处对应的雅可比矩阵\(\mathbf J_{\mathbf f} (\mathbf a)\):
\[\mathbf J_{\mathbf f}(\mathbf a) = \begin{bmatrix} \frac{\partial f_{1}}{\partial x_{1}} & \dots & \frac{\partial f_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}} & \dots & \frac{\partial f_{m}}{\partial x_{n}} \end{bmatrix}_{\mathbf x=\mathbf a}\]6.3.1 状态转移矩阵
对于形如\(\mathbf x_{t} = \mathbf f(\mathbf x_{t-1})\)的状态转移方程,依据一阶泰勒展开公式,在\(\mathbf x_{t-1}\)处展开,有:
\[\mathbf x_{t} \approx \mathbf f(\mathbf x_{t-1})+\frac{\partial \mathbf f}{\partial \mathbf x}|_{\mathbf x = \mathbf x_{t-1}}(\mathbf x - \mathbf x_{t-1})= \mathbf f(\mathbf x_{t-1}) + \mathbf J_{\mathbf f} (\mathbf x_{t-1})(\mathbf x - \mathbf x_{t-1})\]此时,状态转移矩阵就是函数\(\mathbf f(\mathbf x)\)在\(\mathbf x_{t-1}\)位置对应的雅可比矩阵。例如,对于某个轮式机器人做匀速运动(速度大小不变,方向可变),我们可以基于轮速计很容易得到其速度\(v\),同时其搭载了方位测量设备,也可以很容易获得当前的航向\(\theta\)和角速度\(\omega\)。因此,我们的观测量\(\mathbf z = [v, \theta, \omega]^{T}\)。我们希望获得机器人当前最优的位置、航向角、速度,写成状态向量即为\(\mathbf z = [x, y, \theta, v]^{T}\)。对于t-1时刻状态和t时刻状态,我们可以写出如下关系:
\[\left\{\begin{matrix} x_{t} = x_{t-1} + v \cdot cos(\theta_{t-1})\cdot \Delta t\\ y_{t} = y_{t-1} + v \cdot sin(\theta_{t-1})\cdot \Delta t \\ \theta_{t} = \theta_{t-1} + \omega \cdot \Delta t\\ v_{t} = v_{t-1} \end{matrix}\right.\]这个式子是比较容易理解的。上一个状态的位置加上速度在x、y方向上的分量再乘以时间间隔,即可预测出当前时刻位置。这里其实和4.3部分的例子是类似的。只是在那个例子中,\(v_x\)、\(v_y\)直接是状态变量之一,直接乘以dt即可得到对应方向的位置变化。这里是\(v\),所以需要乘以\(cos\)和\(sin\),将其变为\(v_x\)、\(v_y\)。对于航向角,则等于上一状态的角度加上角速度乘以时间间隔得到的角度变化量。对于速度大小,由于认为是匀速运动,所以上一状态速度和当前状态速度相等。对于上面给出的这一组状态转移方程,因为存在非线性的sin和cos。我们对上式对状态向量进行求导,可以得到雅可比矩阵:
\[\mathbf F = \mathbf J_{\mathbf f} = \frac{\partial \mathbf f}{\partial \mathbf x} = \begin{bmatrix} 1 & 0 & -sin(\theta)v\Delta t & cos(\theta) \Delta t\\ 0 & 1 & cos(\theta) v\Delta t & sin(\theta) \Delta t\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\]一般情况,\(\Delta t\)可设为1,再将t-1时刻对应的航向角和速度代入,即可得到状态转移矩阵F。基于它便可以计算预测状态误差。
6.3.2 观测矩阵
和状态转移矩阵类似的。对于形如\(\mathbf z = \mathbf h(\mathbf x)\)的状态转移方程,依据一阶泰勒展开公式,在\(\mathbf x_{t}\)处展开,有:
\[\mathbf z \approx \mathbf h(\mathbf x_{t-1})+\frac{\partial \mathbf h}{\partial \mathbf x}|_{\mathbf x = \mathbf x_{t-1}}(\mathbf x - \mathbf x_{t-1})= \mathbf h(\mathbf x_{t-1}) + \mathbf J_{\mathbf h} (\mathbf x_{t-1})(\mathbf x - \mathbf x_{t-1})\]此时,观测矩阵就是函数\(\mathbf h(\mathbf x)\)在\(\mathbf x_{t-1}\)位置对应的雅可比矩阵。例如,对于某个机器人,其观测是相对于某个已知路标\(L(x_{L}, y_{L})\)的距离\(d\)、路标相对于机器人朝向的夹角\(\alpha\),测量向量为\(\mathbf z = [d, \alpha]^{T}\)。我们关心的状态包括机器人的位置以及航向角,因此状态向量为\(\mathbf x = [x, y, \theta]^{T}\)。首先,基于已知信息写出观测方程,将状态映射到传感器测量值,如下:
\[\left\{\begin{matrix} d = \sqrt{(x_{L}-x)^2+(y_{L}-y)^2} \\ \alpha = arctan(\frac{\mathrm{d} y_{L}-y}{\mathrm{d} x_{L}-x}) - \theta \end{matrix}\right.\]这里两个式子都比较好理解,第一个就是根据机器人的位置和路标点的位置,计算距离。第二个是首先基于机器人位置和路标点位置计算了全局的方位角\(arctan(\frac{\mathrm{d} y_{L}-y}{\mathrm{d} x_{L}-x})\),然后通过减去机器人的航向角\(\theta\),将全局方位角转化为相对于机器人朝向的角度。然后上式对状态向量进行求导。这里需要注意的是,由于观测方程相对复杂,对其求导也较为复杂,涉及链式法则等,感兴趣可以仔细研究。此处为了便于阅读,略过求导过程,直接展示雅可比矩阵:
\[\mathbf H = \mathbf J_{\mathbf h} = \frac{\partial \mathbf h}{\partial \mathbf x} = \begin{bmatrix} -\frac{x_{L}-x}{\sqrt{(x_{L}-x)^2+(y_{L}-y)^2}} & -\frac{y_{L}-y}{\sqrt{(x_{L}-x)^2+(y_{L}-y)^2}} & 0\\ \frac{y_{L}-y}{\sqrt{(x_{L}-x)^2+(y_{L}-y)^2}} & -\frac{x_{L}-x}{\sqrt{(x_{L}-x)^2+(y_{L}-y)^2}} & -1\\ \end{bmatrix}\]将t时刻对应的位置代入,即可得到观测矩阵H。基于它便可以计算卡尔曼增益、更新预测及对应的误差。
7.实际示例
7.1 机器人非线性运动
7.1.2 问题描述
对于某个平面运动的机器人,其携带了距离传感器和角度传感器,可以测量相对于路标的距离和夹角。现要求根据测量,给出机器人平面位置、航向角的最优估计。
7.1.3 问题建模
问题建模可以从前面几个问题开始:
观测量是什么:观测是相对于某个已知路标\(L(x_{L}, y_{L})\)的距离\(d\)、路标相对于机器人朝向的夹角\(\alpha\),测量向量为\(\mathbf z = [d, \alpha]^{T}\)。
希望估计的量是什么:希望估计的状态包括机器人的位置以及航向角,因此状态向量为\(\mathbf x = [x, y, \theta]^{T}\)。
状态间存在什么关联:根据给定的状态和运动模型,可以写出机器人状态之间的转移函数,如下:
\[\left\{\begin{matrix} x_{t} = x_{t-1} + v \cdot cos(\theta_{t-1})\cdot \Delta t\\ y_{t} = y_{t-1} + v \cdot sin(\theta_{t-1})\cdot \Delta t \\ \theta_{t} = \theta_{t-1} + \omega \cdot \Delta t \end{matrix}\right.\]利用上式即可进行状态预测。这里需要说明的是,上式中涉及到的速度\(v\)和角速度\(\omega\)既不属于观测向量也不属于状态向量。那么从哪里获得他们的数值呢?答案是他们是作为外部控制因素直接输入的,卡尔曼滤波不对其进行估计或预测。对于\(\Delta t\)一般可设为1。这样,上式中所有变量均已知,可得到t时刻预测状态。
进一步,对上式求导,得到雅可比矩阵F:
\[\mathbf F = \mathbf J_{\mathbf f} = \frac{\partial \mathbf f}{\partial \mathbf x} = \begin{bmatrix} 1 & 0 & -sin(\theta)v\Delta t\\ 0 & 1 & cos(\theta) v\Delta t\\ 0 & 0 & 1 \end{bmatrix}\]对非线性状态转移函数在t-1时刻线性化,\(\Delta t\)一般可设为1,将对应的航向角和速度代入,即可得到状态转移矩阵F。基于它便可以计算预测状态误差。
系统状态是否有外部因素控制:有,主要是速度\(v\)和角速度\(\omega\),\(\mathbf u = [v, \omega]^{T}\)其直接参与状态预测计算。
状态和观测之间存在什么关联:测量向量为\(\mathbf z = [d, \alpha]^{T}\),状态向量为\(\mathbf x = [x, y, \theta]^{T}\)。根据数学模型可以写出两者的观测函数,如下:
\[\left\{\begin{matrix} d = \sqrt{(x_{L}-x)^2+(y_{L}-y)^2} \\ \alpha = arctan(\frac{y_{L}-y}{x_{L}-x}) - \theta \end{matrix}\right.\]对该函数对状态向量求导,可以得到雅可比矩阵H:
\[\mathbf H = \mathbf J_{\mathbf h} = \frac{\partial \mathbf h}{\partial \mathbf x} = \begin{bmatrix} -\frac{x_{L}-x}{\sqrt{(x_{L}-x)^2+(y_{L}-y)^2}} & -\frac{y_{L}-y}{\sqrt{(x_{L}-x)^2+(y_{L}-y)^2}} & 0\\ \frac{y_{L}-y}{\sqrt{(x_{L}-x)^2+(y_{L}-y)^2}} & -\frac{x_{L}-x}{\sqrt{(x_{L}-x)^2+(y_{L}-y)^2}} & -1\\ \end{bmatrix}\]将t时刻对应的位置估计代入,即可得到观测矩阵H。基于它便可以计算卡尔曼增益、更新预测及对应的误差。
实际观测量的误差怎么样:测量向量为\(\mathbf z = [d, \alpha]^{T}\),假设距离观测方差为0.5,角度观测方差0.17,所以观测噪声矩阵\(\mathbf{R} = \begin{bmatrix} 0.5 & 0\\ 0 & 0.17 \end{bmatrix}\)。
运行过程外部干扰怎么样:假设实际中各种不可预见因素给位置造成方差为0.1的干扰、角度造成0.02干扰,所以\(\mathbf{Q} = \begin{bmatrix} 0.1 & 0 & 0\\ 0 & 0.1 & 0\\ 0 & 0 & 0.02 \end{bmatrix}\)。
初始预测状态怎么样:假设初始观测为\(\mathbf z = [0, 0]^T\),那么初始预测状态\(\mathbf{x} = [0, 0, 0]^{T}\)。对应状态协方差矩阵\(\mathbf{P} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}\)。
7.1.4 代码实现
基于上面给出的公式和确定的参数,最终,可以通过以下代码实现卡尔曼滤波。
import numpy as np
from matplotlib import pyplot as plt
import math
# 给定参数
# 两个状态间的时间间隔
delta_t = 0.1
# 观测矩阵
def getJacobianH(state, landmark_pos):
# 获取从状态向量中获取需要的变量进行计算
cur_x = state[0]
cur_y = state[1]
x_l = landmark_pos[0]
y_l = landmark_pos[1]
dx = x_l - cur_x
dy = y_l - cur_y
d = math.sqrt(dx*dx + dy*dy)
H = np.array([[-dx/d, -dy/d, 0],
[dy/d, -dx/d, -1]])
return H
# 状态转移矩阵
def getJacobianF(state, u, dt):
# 获取从状态向量和控制向量中获取需要的变量进行计算
theta_rad = state[2]
vel = u[0]
F = np.array([[1, 0, -math.sin(theta_rad)*vel*dt],
[0, 1, math.cos(theta_rad)*vel*dt],
[0, 0, 1]])
return F
# 过程噪声协方差矩阵
Q = np.array([[0.1, 0, 0],
[0, 0.1, 0],
[0, 0, 0.02]])
# 测量噪声协方差矩阵
R = np.array([[0.5, 0],
[0, 0.17]])
# 给定路标位置
landmark_pos = np.array([5, 3])
# 控制输入,给定不同阶段的外部控制变量
controls = []
for i in range(100):
# 不同阶段速度不同
if i < 30:
vel = 1.0
omega = 0.2
elif 30 <= i < 70:
vel = 0.8
omega = -0.3
else:
vel = 1.2
omega = 0.1
controls.append([vel, omega])
# 构造理论值,方便评估精度,实际无法获得
# 理想状态,包括 位置x、位置y、航向角theta
ideal_states = []
ideal_states.append([0, 0, 0])
for i in range(1, 100):
x = ideal_states[i-1][0] + controls[i][0] * math.cos(ideal_states[i-1][2]) * delta_t
y = ideal_states[i-1][1] + controls[i][0] * math.sin(ideal_states[i-1][2]) * delta_t
theta = ideal_states[i-1][2] + controls[i][1] * delta_t
ideal_states.append([x, y, theta])
# 根据理论状态值,构造理论观测值和噪声观测值
ideal_measurements = []
noisy_measurements = []
for i in range(len(ideal_states)):
cur_x = ideal_states[i][0]
cur_y = ideal_states[i][1]
cur_theta = ideal_states[i][2]
ideal_d = math.sqrt((landmark_pos[0] - cur_x)**2 + (landmark_pos[1] - cur_y)**2)
ideal_a = math.atan2(landmark_pos[1] - cur_y, landmark_pos[0] - cur_x) - cur_theta
noisy_d = ideal_d + np.random.normal(0, 0.1)
noisy_a = ideal_a + np.random.normal(0, 0.1)
ideal_measurements.append([ideal_d, ideal_a])
noisy_measurements.append([noisy_d, noisy_a])
# 系列观测和外部控制
z = noisy_measurements
u = controls
# 给状态赋初值
prev_state = np.array([0, 0, 0])
prev_error = np.array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
# 用于存放估计的状态
predict_states = []
predict_xs = []
predict_ys = []
# 开始卡尔曼滤波
for i in range(len(z)):
# 预测 - 状态
# predict_state = F @ prev_state + B @ u[i]
x_t = prev_state[0] + u[i][0] * math.cos(prev_state[2]) * delta_t
y_t = prev_state[1] + u[i][0] * math.sin(prev_state[2]) * delta_t
theta_t = prev_state[2] + u[i][1] * delta_t
predict_state = np.array([x_t, y_t, theta_t])
# 预测 - 计算雅可比矩阵F
# 在t-1时刻泰勒展开,所以传入上次的状态
F = getJacobianF(prev_state, u[i], delta_t)
# 预测 - 误差
predict_error = F @ prev_error @ F.T + Q
# 更新 - 计算雅可比矩阵H
# 在t时刻泰勒展开,所以传入当前状态
H = getJacobianH(predict_state, landmark_pos)
# 更新 - 卡尔曼增益
kalman_gain = predict_error @ H.T @ np.linalg.inv(H @ predict_error @ H.T + R)
# 更新 - 状态
update_state = predict_state + kalman_gain @ (z[i] - H @ predict_state)
# 更新 - 误差
update_error = (np.eye(3) - kalman_gain @ H) @ predict_error
# 变量赋值开启下次迭代
prev_state = update_state
prev_error = update_error
# 将预测状态保存起来
predict_states.append(update_state)
predict_xs.append(update_state[0])
predict_ys.append(update_state[1])
# 可视化
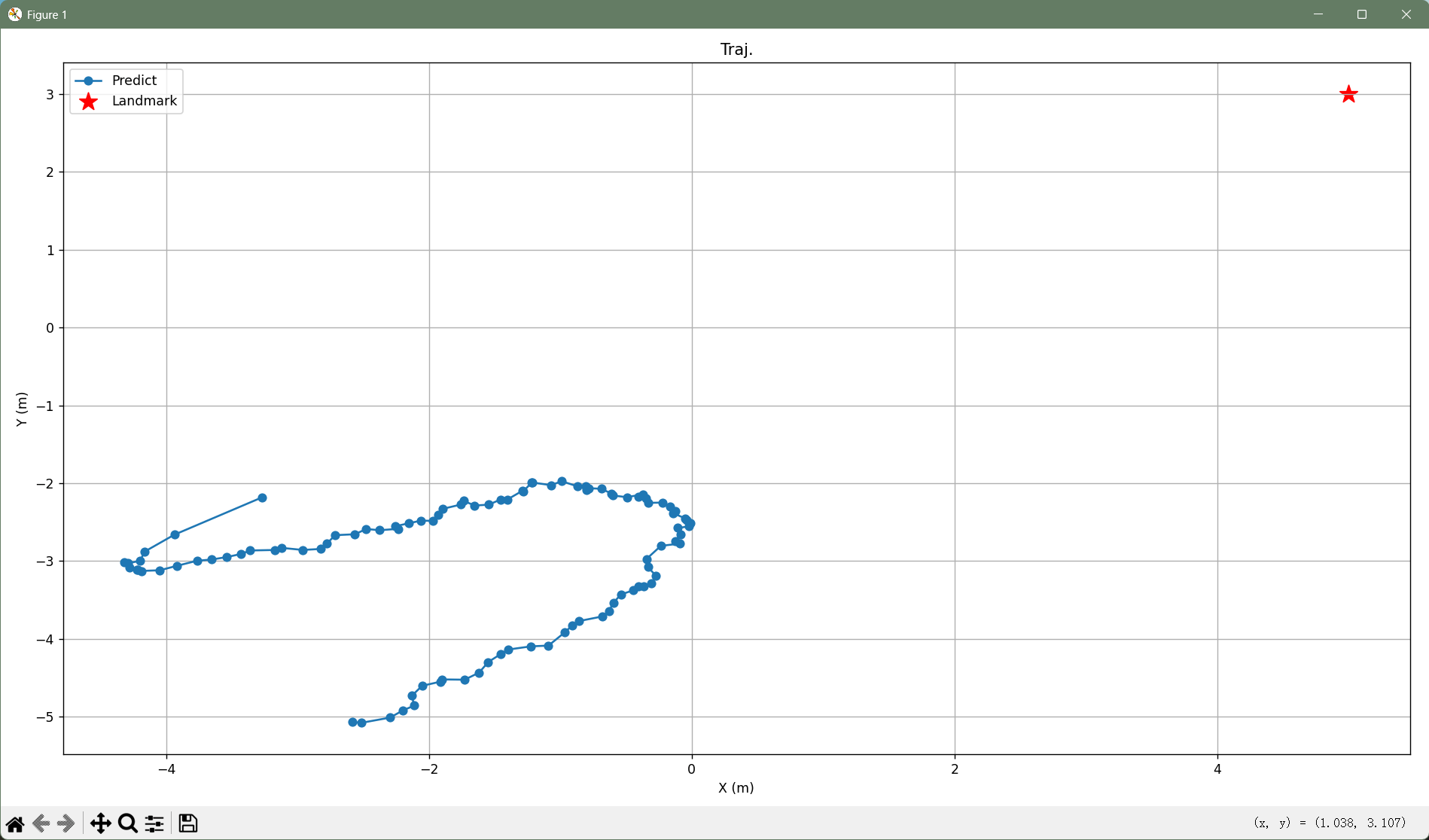
plt.figure(figsize=(10, 6))
plt.plot(predict_xs, predict_ys, 'o-', label='Predict')
plt.scatter(*landmark_pos, c='red', marker='*', s=200, label='Landmark')
plt.legend()
plt.title('Traj.')
plt.xlabel('X (m)')
plt.ylabel('Y (m)')
plt.grid(True)
plt.show()
运行后效果如下:
7.2 多传感器融合
下面代码展示了IMU和GPS传感器融合。
import numpy as np
from scipy.linalg import expm
# 系统参数初始化
dt = 0.01 # 采样时间间隔(秒)
state_dim = 9 # 状态维度 [位置x,y,z, 速度vx,vy,vz, 加速度bias ax_b,ay_b,az_b]
state = np.zeros(state_dim) # 初始状态
P = np.eye(state_dim) * 10 # 初始协方差矩阵
# IMU噪声参数
gyro_noise = 0.001 # 陀螺仪噪声(rad/s)
accel_noise = 0.01 # 加速度计噪声(m/s²)
bias_noise = 1e-5 # 加速度计偏置噪声
# GPS噪声参数
gps_pos_noise = 0.5 # 位置测量噪声(m)
# 过程噪声矩阵
Q = np.diag([0.1, 0.1, 0.1, 0.05, 0.05, 0.05, 0.01, 0.01, 0.01])
# 观测噪声矩阵
R_gps = np.diag([gps_pos_noise, gps_pos_noise, gps_pos_noise])
def skew(v):
"""计算向量v的斜对称矩阵"""
return np.array([[0, -v[2], v[1]],
[v[2], 0, -v[0]],
[-v[1], v[0], 0]])
def rotation_matrix(phi, theta, psi):
"""计算旋转矩阵(滚转phi, 俯仰theta, 偏航psi)"""
R_x = np.array([[1, 0, 0],
[0, np.cos(phi), -np.sin(phi)],
[0, np.sin(phi), np.cos(phi)]])
R_y = np.array([[np.cos(theta), 0, np.sin(theta)],
[0, 1, 0],
[-np.sin(theta), 0, np.cos(theta)]])
R_z = np.array([[np.cos(psi), -np.sin(psi), 0],
[np.sin(psi), np.cos(psi), 0],
[0, 0, 1]])
return R_z @ R_y @ R_x
def predict(imu_accel, imu_gyro):
"""EKF预测步骤(处理IMU数据)"""
global state, P
# 解包状态变量
x, y, z, vx, vy, vz, ax_b, ay_b, az_b = state
# 估计姿态(简化的四元数更新)
phi, theta, psi = 0, 0, 0 # 实际应用中需通过陀螺仪积分计算
R = rotation_matrix(phi, theta, psi)
# 校正加速度计偏置
corrected_accel = imu_accel - [ax_b, ay_b, az_b]
# 将加速度转换到全局坐标系
global_accel = R @ corrected_accel + np.array([0, 0, -9.81])
# 非线性状态转移函数
def f(x):
px, py, pz, vx, vy, vz, ax_b, ay_b, az_b = x
return np.array([
px + vx * dt + 0.5 * global_accel[0] * dt**2,
py + vy * dt + 0.5 * global_accel[1] * dt**2,
pz + vz * dt + 0.5 * global_accel[2] * dt**2,
vx + global_accel[0] * dt,
vy + global_accel[1] * dt,
vz + global_accel[2] * dt,
ax_b,
ay_b,
az_b
])
# 计算雅可比矩阵
F = np.eye(state_dim)
F[0, 3] = dt # ∂x/∂vx
F[1, 4] = dt # ∂y/∂vy
F[2, 5] = dt # ∂z/∂vz
F[3, 6:9] = -R[0] * dt # ∂vx/∂bias
F[4, 6:9] = -R[1] * dt # ∂vy/∂bias
F[5, 6:9] = -R[2] * dt # ∂vz/∂bias
# 状态预测
state = f(state)
# 协方差预测
P = F @ P @ F.T + Q
def update_gps(gps_pos):
"""EKF更新步骤(处理GPS数据)"""
global state, P
# 观测矩阵(GPS直接观测位置)
H = np.array([
[1, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0, 0]
])
# 卡尔曼增益计算
S = H @ P @ H.T + R_gps
K = P @ H.T @ np.linalg.inv(S)
# 状态更新
innovation = gps_pos - state[:3]
state += K @ innovation
# 协方差更新
P = (np.eye(state_dim) - K @ H) @ P
# 姿态归一化(实际应用中需处理四元数)
# 主函数
def main():
# 模拟数据
np.random.seed(42)
# 真实轨迹(圆周运动)
t = 0
radius = 50
angular_vel = 0.1
for step in range(1000):
t = step * dt
# 生成真实状态
true_pos = np.array([
radius * np.cos(angular_vel * t),
radius * np.sin(angular_vel * t),
10.0
])
true_vel = np.array([
-radius * angular_vel * np.sin(angular_vel * t),
radius * angular_vel * np.cos(angular_vel * t),
0
])
# 生成IMU测量值(含噪声)
imu_accel = true_vel * angular_vel + np.random.normal(0, accel_noise, 3)
imu_gyro = np.array([0, 0, angular_vel]) + np.random.normal(0, gyro_noise, 3)
# 生成GPS测量值(含噪声)
if step % 10 == 0: # GPS频率10Hz
gps_data = true_pos + np.random.normal(0, gps_pos_noise, 3)
# EKF处理
predict(imu_accel, imu_gyro)
if step % 10 == 0:
update_gps(gps_data)
# 每100步输出结果
if step % 100 == 0:
print(f"Step {step}: Pos={state[:3]}, Vel={state[3:6]}")
if __name__ == "__main__":
main()
本文作者原创,未经许可不得转载,谢谢配合
