通往MSCKF的道路1：概率论基础知识笔记

0.前言
1.概率论基本知识
2.似然(Likelihood)
- 似然函数
- 最大似然估计
3.贝叶斯框架
4.参考资料

0.前言

之所以整理这篇博客，原因在于在学习MSCKF(Multi State Constraint Kalman Filter,多状态约束卡尔曼滤波)的时候发现很多东西都理解不了，于是追根溯源，找到EKF(Extend Kalman Filter,扩展卡尔曼滤波)、KF(Kalman Filter,卡尔曼滤波)、HMM(Hidden Markov Model,隐马尔可夫模型)、GMM(Gaussian Mix Model,高斯混合模型)等等，一路回溯到了概率论的基本知识。如果你在看KF或者EKF或者MSCKF的时候摸不着头脑，那么这一系列的笔记也许会对你有帮助。当按顺序看完这些背景知识后，再理解卡尔曼滤波就会相对简单了。为了不增加额外的学习负担，对于那些在KF中用不到的知识就不再提了。个人总结的MSCKF的学习路径如下，各个知识点之间的关系不一定正确，欢迎指正。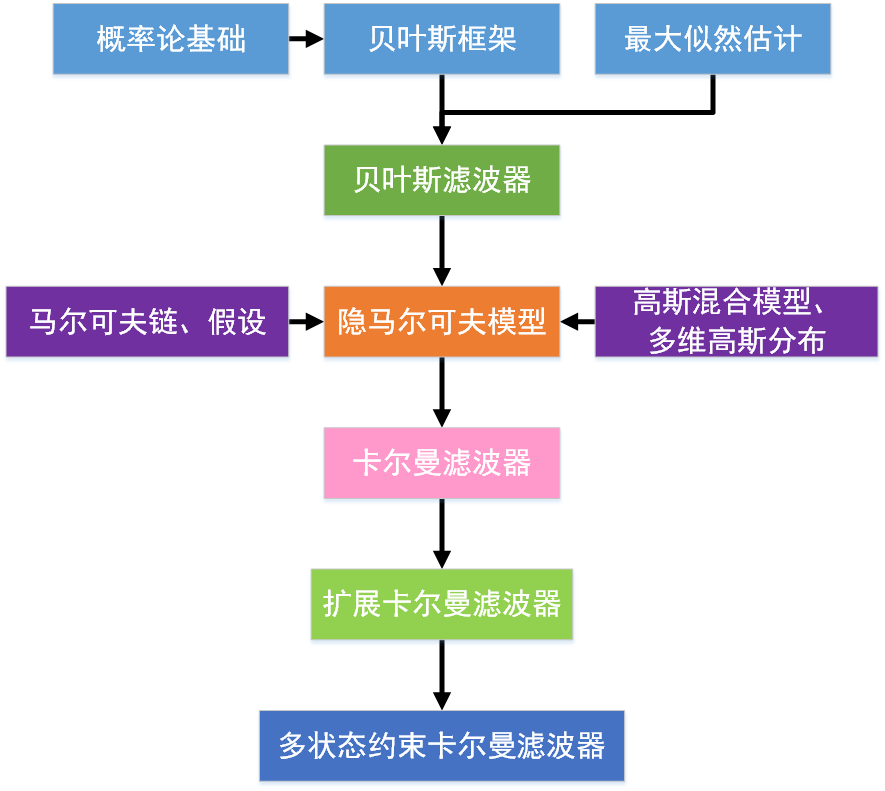本篇博客主要记录在后续能用到的概率论基本知识，包含概率论基础、贝叶斯框架和最大似然估计。

1.概率论基本知识

本部分的一些基本内容来自慕课的概率论与数理统计课程，网址见参考资料1。

概率(Probability)

概率是指某个事件发生的可能性，随机事件A发生的可能性记作\(P(A)\)或\(Prob(A)\)。例如事件A是抛一枚硬币为正面的情况，那么理论上\(P(A)=\frac{1}{2}\)。概率有三个基本性质：非负性(概率大于等于0)、规范性(必然事件概率为1)、可列可加性(对于两两不相容事件，和事件的概率等于各事件概率值之和)。

概率计算的简单总结如下：

联合概率(联合分布)

表示两个事件共同发生的概率。A与B的联合概率表示为\(P(AB)\)、\(P(A,B)\)或\(P(A∩B)\)。

边缘概率(边缘分布)

边缘概率概念应用在多维随机变量中且相对于联合概率而言。边缘分布(Marginal Distribution)指在多维随机变量中只包含其中部分变量的概率分布(类似于函数中的偏导数概念)。

边缘概率是这样得到的：在联合概率中，把最终结果中不需要的那些事件合并成其事件的全概率而消失(对离散随机变量用求和得全概率，对连续随机变量用积分得全概率)。

条件概率与条件概率公式

条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为:\(P(A\mid B)\)，可以理解为是A在B中所占的比例。\(P(X\mid B)\)可以理解为将样本空间缩小到了B，在B中求各事件的概率。基本的条件概率公式如下：

\[P(A\mid B)=\frac{P(AB)}{P(B)}\]

表示在事件B发生的条件下事件A发生的概率(The probability of A conditioning on B)。当然，上面的式子还可以写成乘法的形式：

\[P(AB)=P(A\mid B)P(B)\]

以上说的是在单一事件发生的条件下的条件概率，对于多个条件，写法也一样：

\[P(A\mid B_{1},B_{2},...B_{n})=\frac{P(A,B_{1},B_{2},...,B_{n})}{P(B_{1},B_{2},...,B_{n})}\]

这就表示事件A在\(B_{1},B_{2},...B_{n}\)都发生的情况下发生的概率。

全概率与全概率公式

全概率简单而言就是有多种达到某个目的方式，达到目的的总概率。或者有多种造成某种结果的原因，造成这种结果的总概率。设\(B_1,B_2,...,B_n\)为样本空间\(S\)的一个划分(不漏、不重)，且\(P(B_i)>0\)，如下图所示。则有全概率公式：

\[P(A)=\sum_{j=1}^{n}P(B_{j})\cdot P(A\mid B_{j})\]

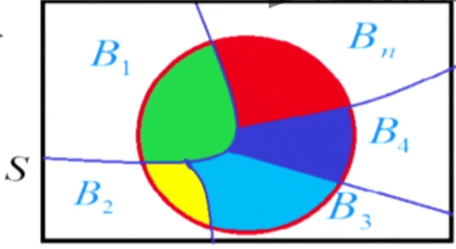
对于累加的每一项，可以用条件概率的乘法公式写成\(P(AB_j)\)。这样全概率公式就可以写成：

\[P(A)=\sum_{j=1}^{n}P(AB_{j})\]

随机变量

随机变量表示的是样本空间与实数空间之间的多对一映射，一般用大写英文字母或希腊字母表示。根据随机变量取值范围的不同，包含离散型随机变量和连续型随机变量两大类。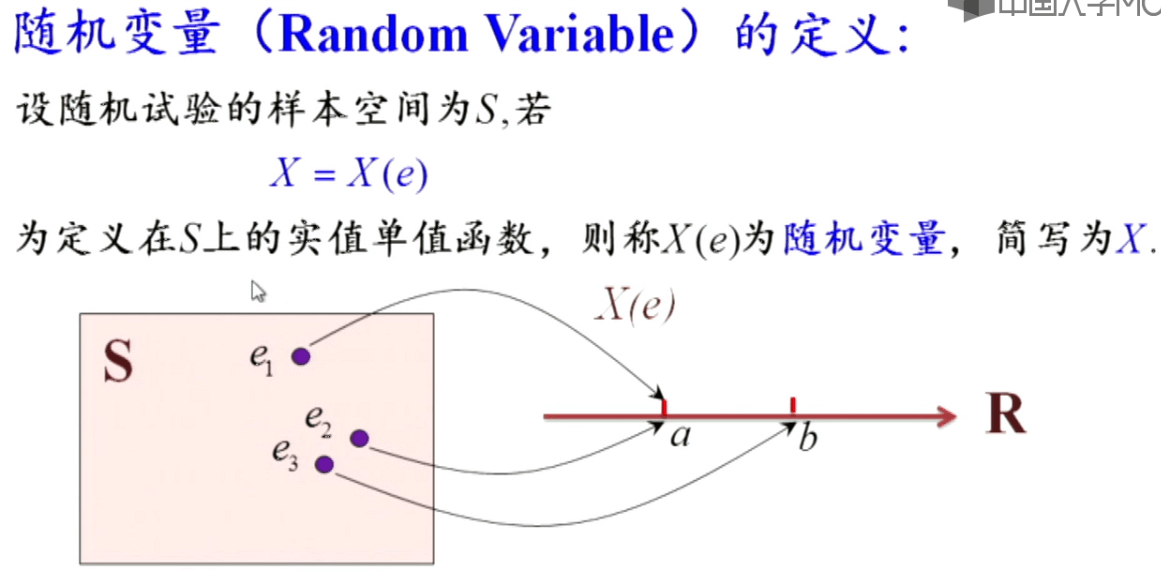随机变量虽然叫“变量”但其本质上是一个“函数”，这点需要注意。

概率分布函数

Probability Distribution Function，PDF。它的几何意义就表示某个事件落到从负无穷到某个点x这个区间的可能性大小，是一个概率。概率分布函数可以给出随机变量落入某个区间的概率。分布函数有如下性质：

有界性，\(0\leq F(x)\leq 1\)
\(F(x)\)单调不减
极限为常数，\(F(-\infty )=0,F(+\infty)=1\)
\(F(x)\)是右连续函数，即\(F(x+0)=F(x)\)

概率密度函数

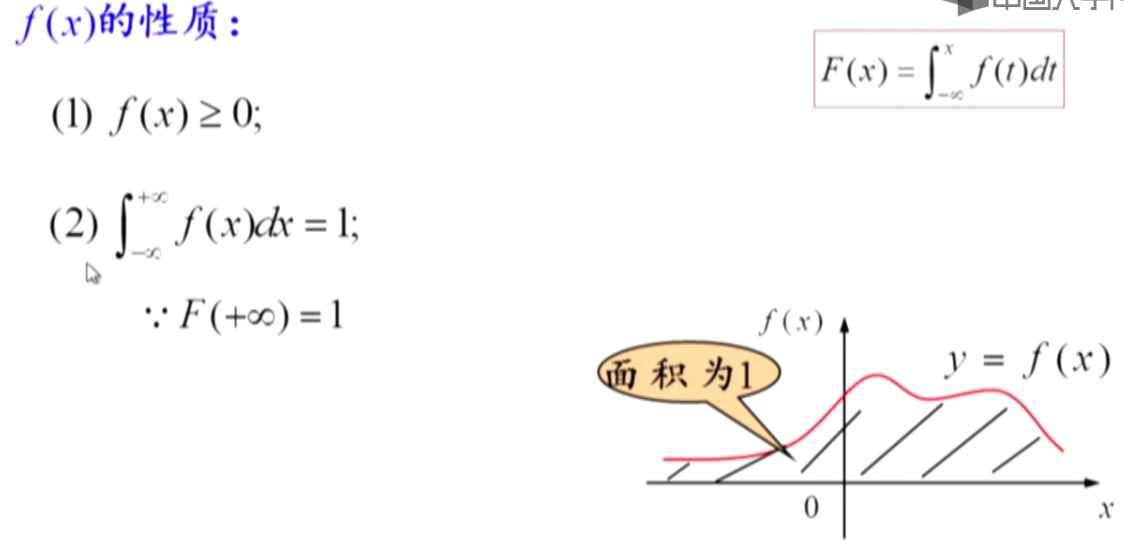
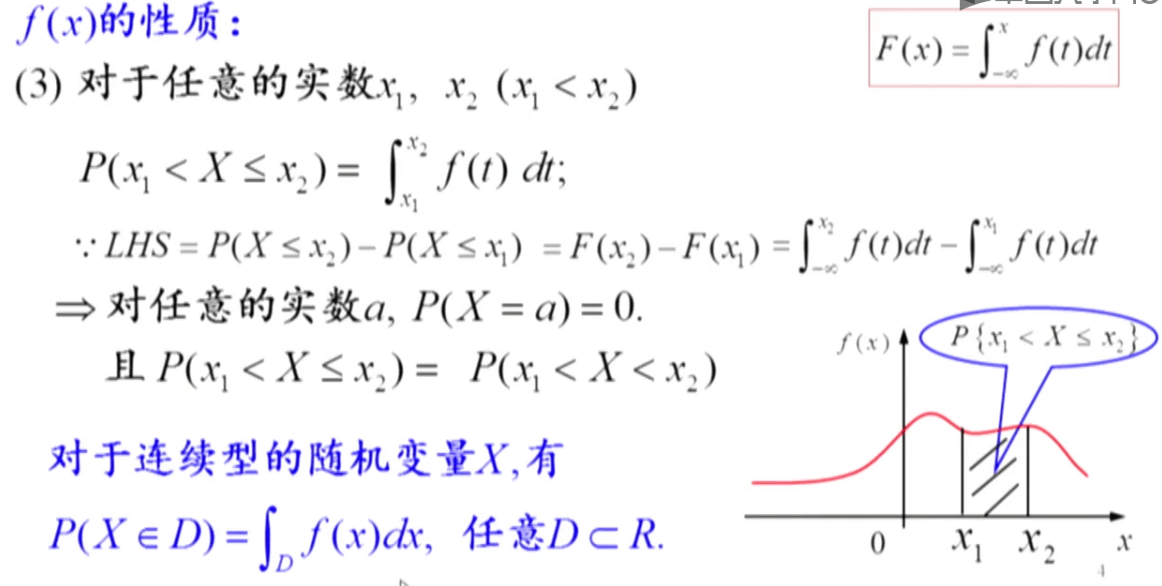
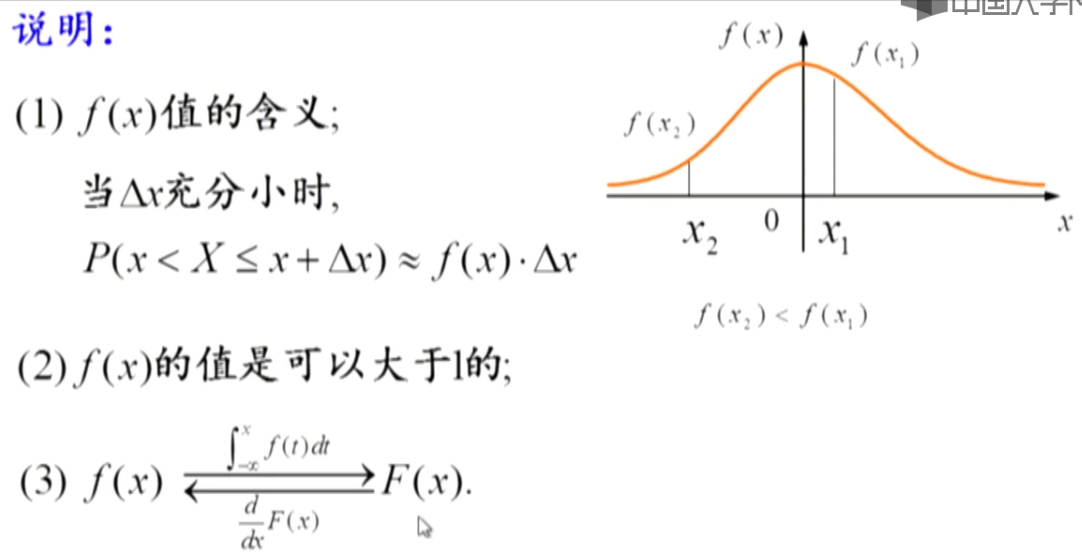
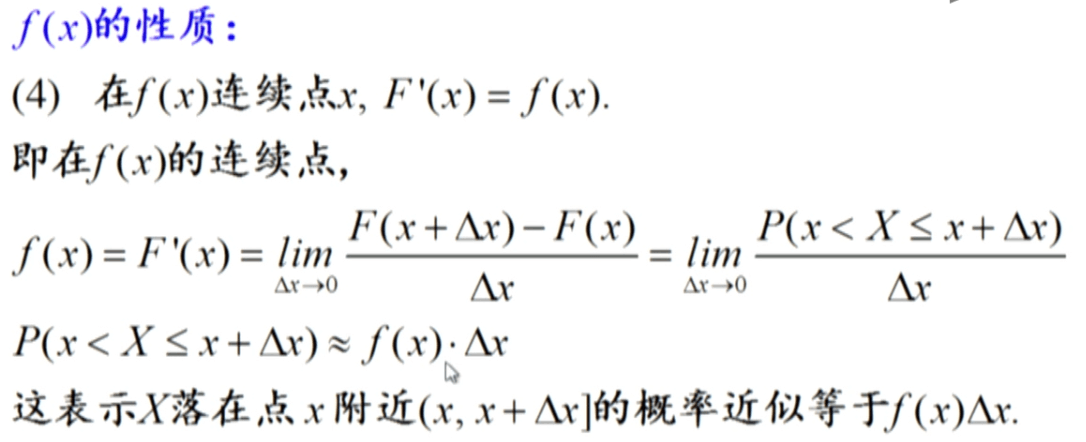Probability Density Function,PDF。概率密度函数是对于连续型随机变量而言的。连续型随机变量一定有对应的概率密度函数，反之亦然。概率密度函数有以下四条性质：概率密度函数值的意义：

高斯分布

又称正态分布。一维随机变量的高斯分布概率密度函数(PDF)为：

\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

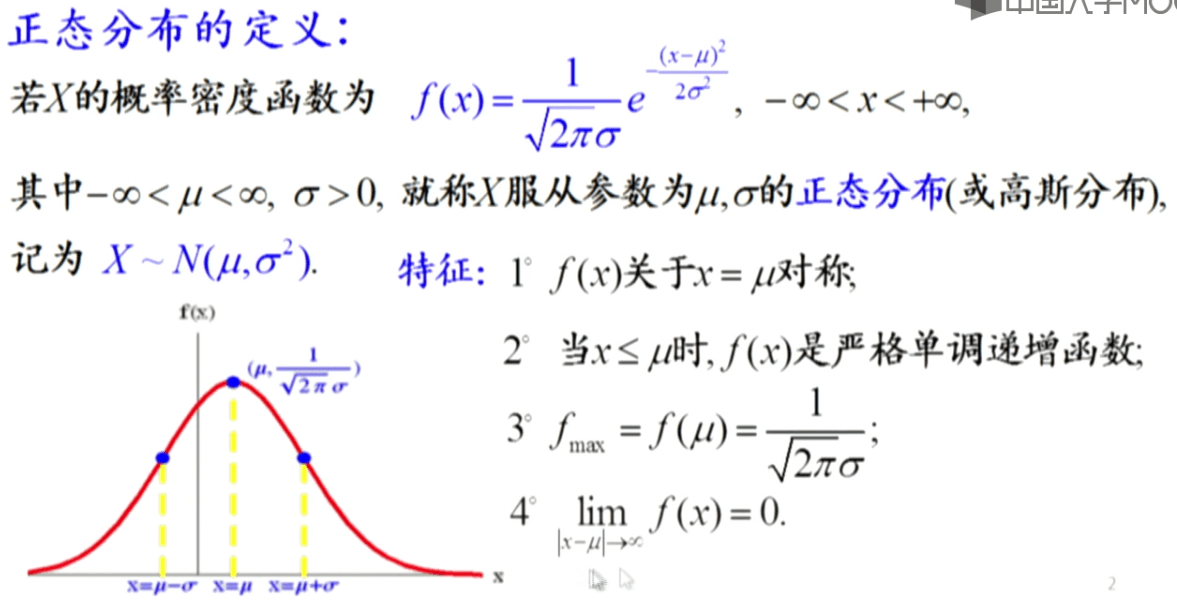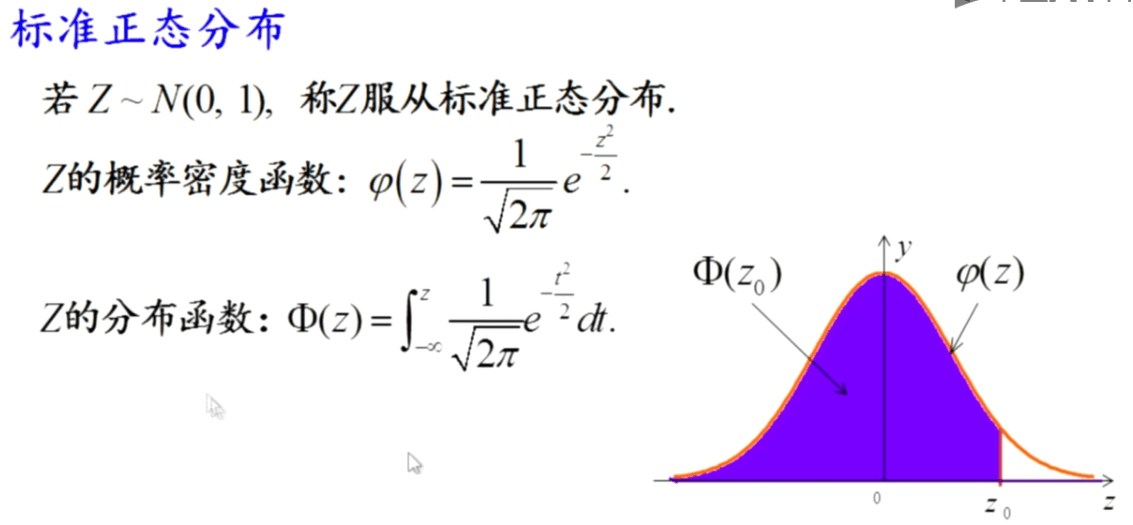
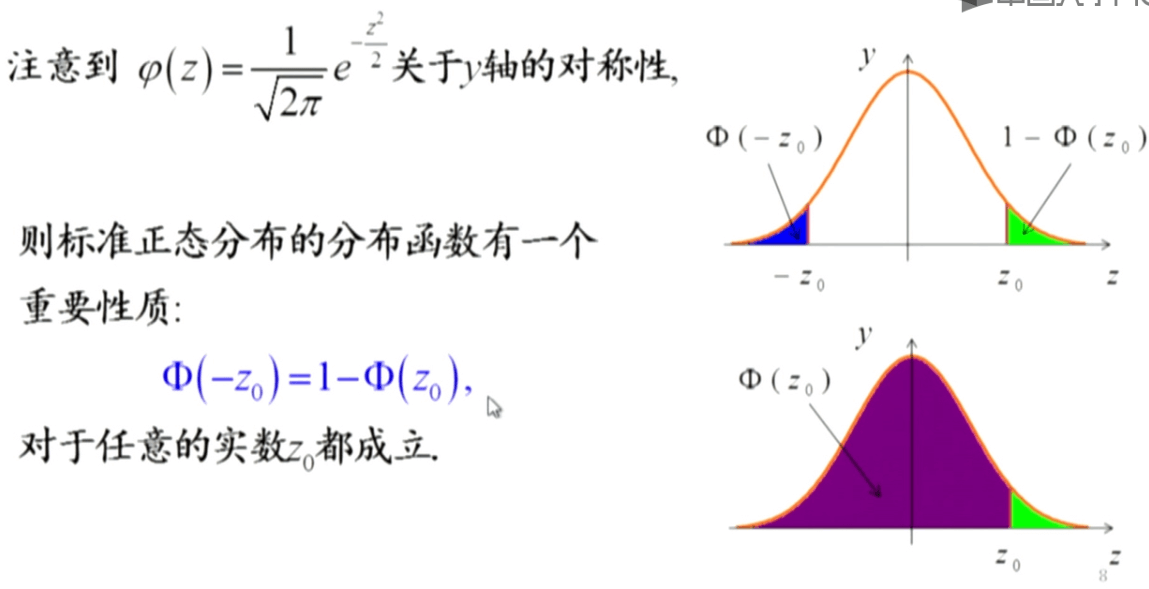
这时就称随机变量X服从参数为μ、σ的高斯分布，记为\(X\sim N(\mu,\sigma^2)\)。有如下性质： μ一般称为位置参数，决定了对称轴的位置。而σ称为尺度参数，决定了曲线的分散程度，即概率密度函数的“胖瘦”。 如果某个随机变量服从均值为0，方差为1的正态分布，\(X\sim N(0,1)\)，就称它为标准正态分布。在概率统计中，一般用\(\varphi\)表示标准正态分布的概率密度函数，用\(Phi\)表示标准正态分布的概率分布函数。对于任意一个正态分布，都可以将其转化为标准正态分布。这个性质很有用，在后面推导任意高斯分布的期望和方差的时候就用到了这个性质。

随机变量函数的分布

这个求随机变量线性变换后的分布的方法很重要，在后面卡尔曼滤波中会用到。

二维随机变量

与一维随机变量类似，二维随机变量也分为离散型和连续型。包含三个方面的研究内容：联合分布、边际分布以及条件分布。

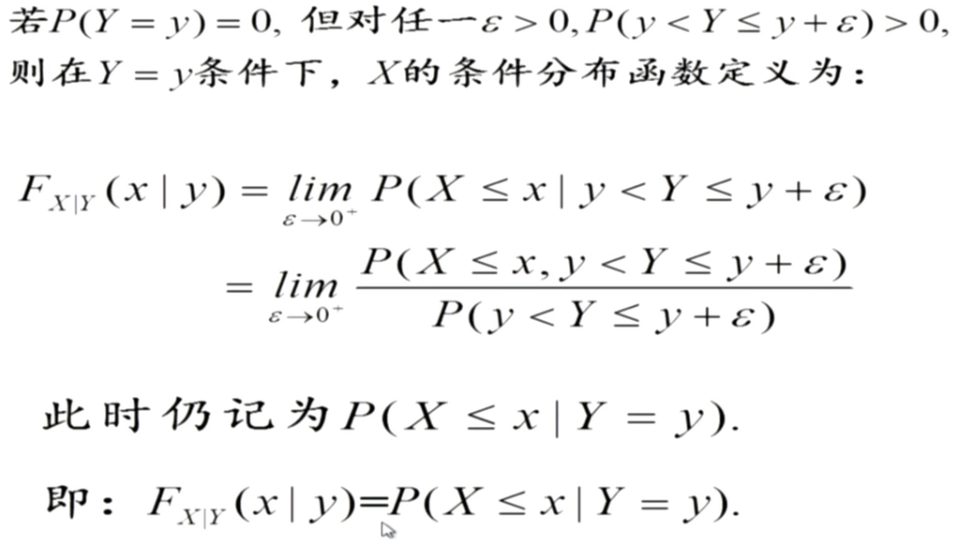
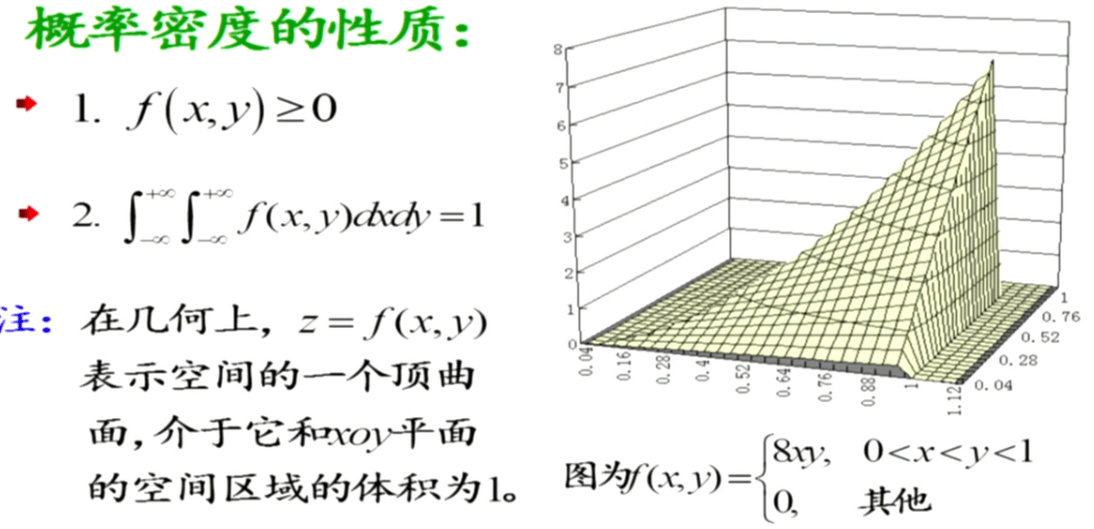
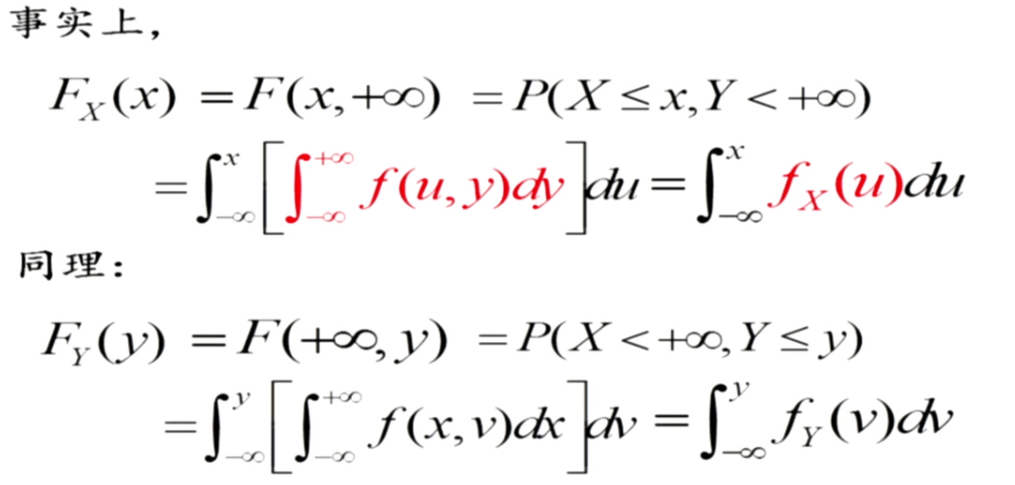
二元随机变量函数的分布

随机变量与随机变量函数的数学期望

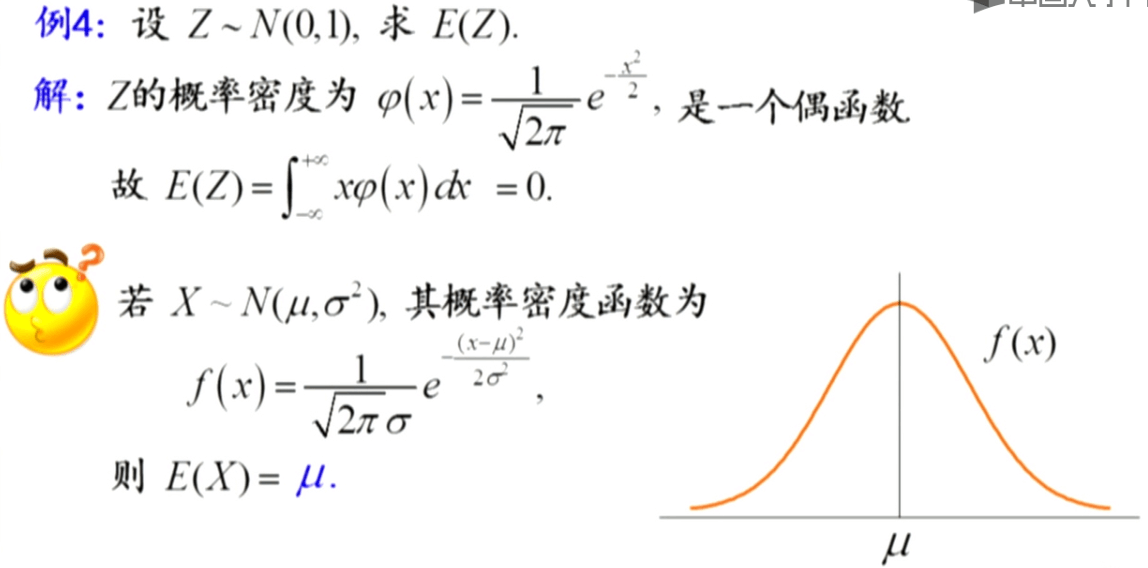
随机变量的方差

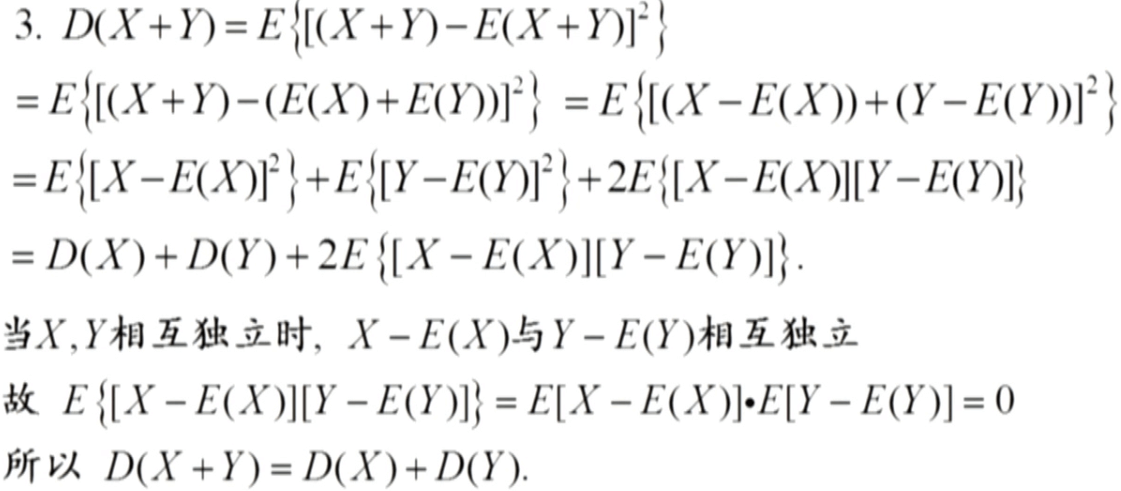
协方差与相关性

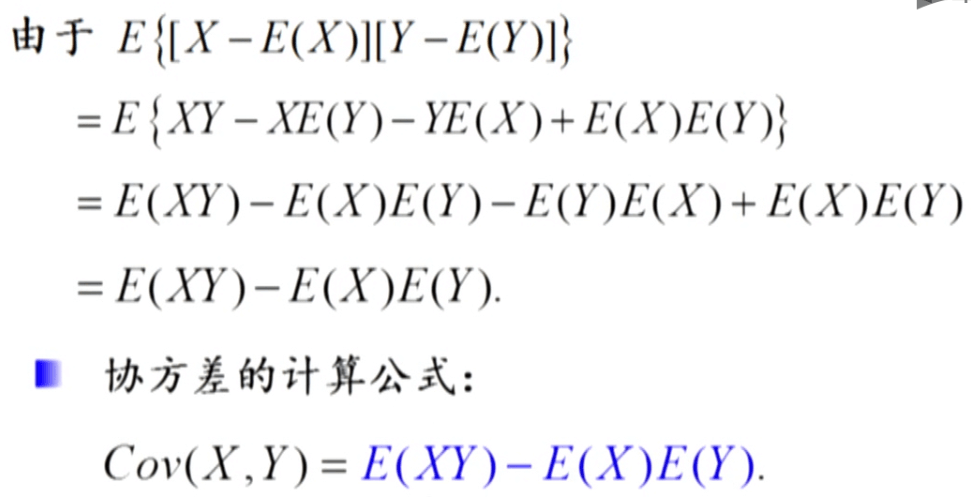
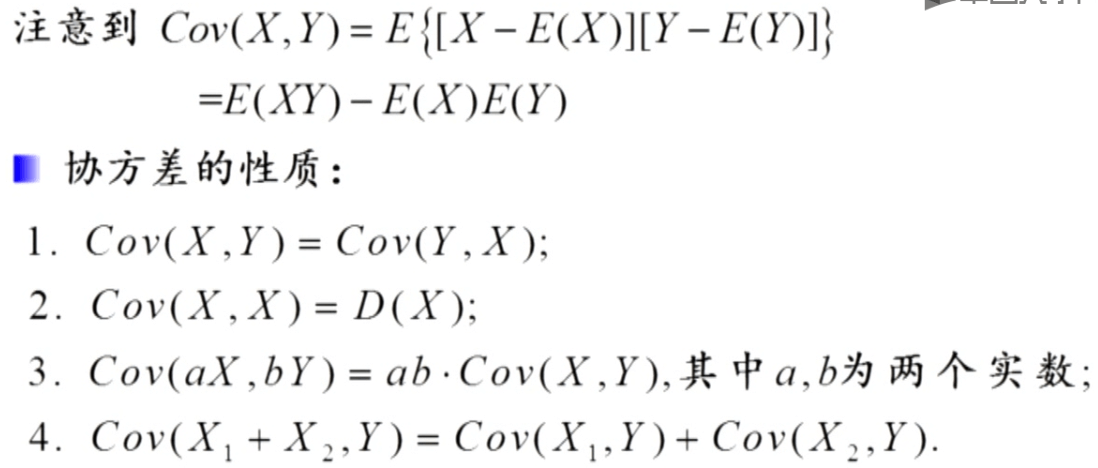
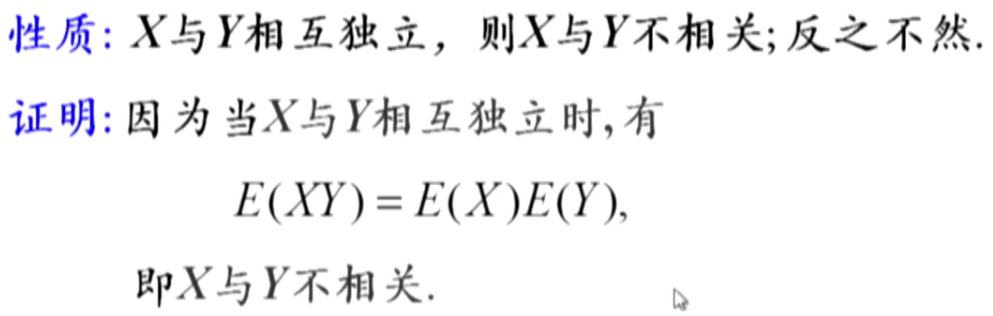
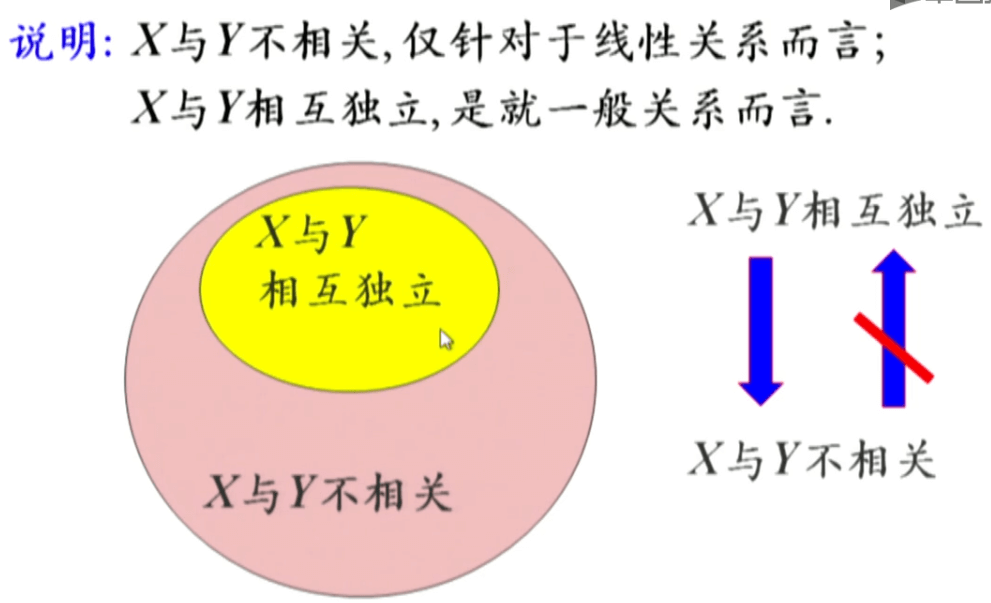
矩

矩是一个统计学上的概念，它的本质是一个数，不要觉得非常神秘。

多维随机变量的期望与协方差

多维高斯分布

2.似然(Likelihood)

似然函数

在数理统计学中，似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。在统计学中，“似然性”和“概率”(或然性)又有明确的区分：概率，用于在已知一些参数的情况下，预测接下来在观测上所得到的结果；似然性，则是用于在已知某些观测所得到的结果时，对有关事物之性质的参数进行估值。给定输出x时，关于参数θ的似然函数\(L(\theta\mid x)\)(在数值上)等于给定参数θ后变量X的概率：\(L(\theta\mid x)=P(X=x\mid \theta)\)。

最大似然估计

在统计学中，最大似然估计(maximum likelihood estimation，缩写为MLE)，也称极大似然估计、最大概似估计，是用来估计一个概率模型的参数的一种方法。最大似然估计的目的就是：利用已知的样本结果，反推最有可能(最大概率)导致这样结果的参数值。极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

3.贝叶斯框架

概述

在概率论中有频率派与贝叶斯派两种不同的思考方式：

频率派把需要推断的参数θ看做是固定的未知常数，即概率θ虽然是未知的，但最起码是确定的一个值，同时，样本X是随机的，所以频率派重点研究样本空间，大部分的概率计算都是针对样本X的分布
而贝叶斯派的观点则截然相反，他们认为参数θ是随机变量，而样本X是固定的，由于样本是固定的，所以他们重点研究的是参数θ的分布

贝叶斯派既然把θ看做是一个随机变量，所以要计算θ的分布，便得事先知道θ的无条件分布，即在有样本之前(或观察到X之前)θ的分布，这种在实验之前定下的属于基本前提性质的分布称为先验分布，或的无条件分布。可以简单理解为先验分布是一种理论上的分布。例如抛掷一枚硬币的正反面，其服从0-1分布。但实际可能硬币两面重量不同，最终的结果就是导致观测得到的正反面次数并不满足0-1分布。

贝叶斯认为概率本身是个不确定的值，因为其中含有机遇的成分。例如在一个盒子中有3个黑球7个白球，问取到黑球的概率是多少。在频率派看来，结果只有黑白两种情况，白球的事件占总可能的1/2，所以不管盒子中的黑白球数量如何变化，概率都为1/2。而在贝叶斯看来，取到黑球的概率与黑、白球的数量有关系，因此取到黑球的概率是3/10。

贝叶斯及贝叶斯派提出了一个思考问题的固定模式：

先验分布\(π(\theta)\) + 样本信息\(X\) ⇒ 后验分布\(\pi(\theta \mid x)\)

新观察到的样本信息将修正对之前事物的认知。换言之，在得到新的样本信息之前，人们对的认知是先验分布\(π(θ)\)，在得到新的样本信息后\(X\)，人们对\(\theta\)的认知为\(π(θ\mid x)\)。而后验分布\(π(θ\mid x)\)一般也认为是在给定样本X的情况下θ的条件分布，而使达到最大的值称为最大后验估计，类似于经典统计学中的极大似然估计。

如果之前有稍微了解过卡尔曼滤波KF就知道，这其实就是卡尔曼滤波KF的核心思想之一：估计值=预测值+观测值。基于状态转移方程实现对当前t时刻先验分布的预测，同时又对此时进行了观测得到样本信息。通过对预测值与观测值根据可靠性(误差大小)进行加权取平均，即可得到认为是最可靠的估计值。所以说卡尔曼滤波KF是在贝叶斯框架下的滤波方法。

综合起来看，则好比是人类刚开始时对大自然只有少得可怜的先验知识，但随着不断是观察、实验获得更多的样本、结果，使得人们对自然界的规律摸得越来越透彻。所以，贝叶斯方法既符合人们日常生活的思考方式，也符合人们认识自然的规律，经过不断的发展，最终占据统计学领域的半壁江山，与经典统计学分庭抗礼。

先验概率

在贝叶斯框架中，边缘概率又称为先验概率(Prior probability)，有时也称作标准化常量(Normalized constant)。例如在事件B发生之前，我们可以对A有个基本的概率判断，称为A的先验概率，用\(P(A)\)表示。

后验概率

在贝叶斯框架中，条件概率又称为后验概率(Posterior probability)。例如当事件B发生后，我们对事件A发生的概率重新评估，称为A的后验概率，用\(P(A\mid B)\)表示。

贝叶斯公式

贝叶斯公式描述了随机事件A和B的先验概率(条件概率)与后验概率(边缘概率)的关系，一句话来描述贝叶斯公式就是：在已知某个结果的情况下，导致该结果的第i个原因的概率(可能性)有多大。

\[P(A_{i}\mid B)=\frac{P(B\mid A_{i})P(A_{i})}{\sum_{j}^{ }P(B\mid A_{j})P(A_{j})}\]

如果对上面说过的全概率公式有印象的话会发现，分母其实就是一个全概率公式，表示的是在事件Aj发生的条件下，事件B发生的总概率。而分子根据条件概率的乘法公式就是Ai和B同时发生的概率\(P(A_i B)\)。所以贝叶斯公式也可以理解为条件概率=联合概率/全概率。

其实贝叶斯公式与条件概率公式是有“异曲同工之妙”的，它们求的都是在某个事件发生的情况(结果)下，另一个事件的发生概率。不同的是，条件概率密度里分母是边际概率，而贝叶斯公式里分母是全概率，这是因为它们应用的场景不一样。在条件概率公式中因果关系可以看作是“一一对应”的，一个原因只会导致一个结果，所以它发生就发生了，不需要用全概率公式计算总发生概率；而在贝叶斯公式中因果关系可以是“一一对应”或者“多对一对应”。在“多对一”的情况时，就需要用全概率公式计算某个事件发生(产生结果)的总可能性了。例如有某个事件A，其发生的概率是\(P(A)\)，若因果一一对应，对于“A发生”这个结果而言，\(P(A)\)就是全概率(因为不存在其它可能性导致A发生了)。但若因果“多对一”对应，则“A发生”则包含多个可能性，需要用全概率公式将这些可能性加起来，才能得到最终的概率。

回顾上面提到的条件概率公式，如下：

\[\begin{matrix} P(A\mid B)=\frac{P(AB)}{P(B)}\\ P(B\mid A)=\frac{P(AB)}{P(A)} \end{matrix}\]

因此对于\(P(A\mid B)\)中的\(P(AB)\)可以用第二个式子中的\(P(AB)\)代替。如果说在因果关系一一对应的情况下，贝叶斯公式可以有如下形式，它与条件概率公式等价。

\[P(A\mid B)=\frac{P(B\mid A)P(A)}{P(B)}=\frac{P(B\mid A)}{P(B)}\cdot P(A)\]

对于事件A而言，上式便反应了它的先验(边缘)概率\(P(A)\)与B事件发生后的后验(条件)概率\(P(A\mid B)\)的关系。上式中\(P(B\mid A)\)有时也称为似然度，\(P(B)\)称为标准化常量，所以贝叶斯公式按术语也可以描述为：后验概率 = (似然度 * 先验概率)/标准化常量。也就是说后验概率与先验概率和似然度的乘积成正比。另一种描述方式是：上式中\(P(B\mid A)/P(B)\)有时也被称作标准似然度(Standardised likelihood)，因此贝叶斯法则也可以表述为：后验概率 = 标准似然度 * 先验概率。

当我们求解一个后验概率时，不妨先预估一个”先验概率”，然后加入观测结果，看这个观测到底是增强还是削弱了”先验概率”，由此得到更接近事实的”后验概率”。如果标准似然度\(P(B\mid A)/P(B)>1\)，意味着”先验概率”被增强，事件A的发生的可能性变大；如果标准似然度=1，意味着B事件无助于判断事件A的可能性；如果标准似然度<1，意味着”先验概率”被削弱，事件A的可能性变小。

一个例子

下面举一个简单的例子，可以更好地帮助理解全概率公式和贝叶斯公式。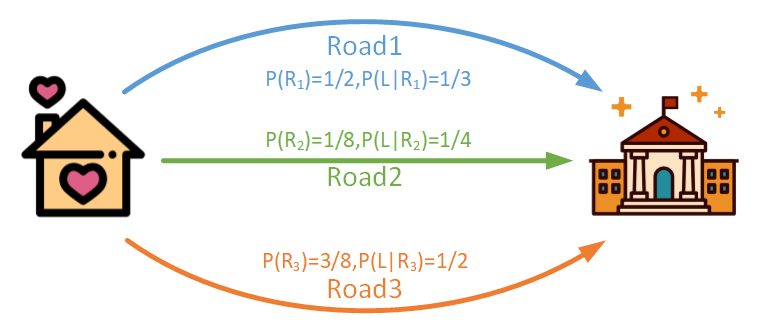例如从家到学校有三条道路，分别是Road1、Road2和Road3，去上学选择Road1的概率是1/2，选Road2上学的概率是1/8，选Road3上学的概率是3/8；选Road1上学迟到的概率是1/3，选Road2上学迟到的概率是1/4，选Road3上学迟到的概率是1/2。

问题1：从家到学校上学不迟到的概率是多少？

这其实是一个典型的全概率公式的应用场景：有多种方式会导致同一个结果，问导致这个结果的可能性有多少。也就是某事件发生的概率乘以该事件发生时导致该结果的概率，对多个概率求和即为结果。根据题目已知，结合全概率公式可以很容易列出下式：

\[P(NotLate)=\frac{1}{2}\times (1-\frac{1}{3})+\frac{1}{8}\times (1-\frac{1}{4})+\frac{3}{8}\times (1-\frac{1}{2})=\frac{59}{96}\]

问题2：在已经上学迟到的情况下，选择Road2的概率是多少？

这里是要求一个条件概率，“由果索因”，可以使用贝叶斯公式。

\[P(R_{2}\mid Late)=\frac{P(Late\mid R_{2})P(R_{2})}{\sum_{j=1}^{3} P(Late\mid R_{j})P(R_{j})}\]

将具体概率带入有：

\[P(R_{2}\mid Late)=\frac{\frac{1}{4}\times \frac{1}{8}}{\frac{1}{3}\times \frac{1}{2}+\frac{1}{4}\times \frac{1}{8}+\frac{1}{2}\times \frac{3}{8}}=\frac{3}{37}\]

4.参考资料

[1]https://www.icourse163.org/course/ZJU-232005
[2]https://zh.wikipedia.org/wiki/似然函数
[3]https://zh.wikipedia.org/wiki/最大似然估计
[4]https://zh.wikipedia.org/wiki/贝叶斯定理
[5]https://www.cnblogs.com/zhoulujun/p/8893393.html
[6]https://blog.csdn.net/qq_39355550/article/details/81809467
[7]https://blog.csdn.net/Hearthougan/article/details/75174210

Menu