拍过星星的同学应该都知道，要想拍出长长的、漂亮的星轨有两种方式：一种就是“简单粗暴”的超长时间曝光，如一次曝光20分钟等。这种方法的好处是后期无需合成处理，所拍即所得，方便省事。它的坏处也显而易见，由于超长时间曝光，非常容易造成过曝问题。即使使用最低感光度如ISO100，也会有最大曝光的上限，一旦超过这个时间就过曝了，比较不好控制。
另一种则是“堆栈式”方法，也就是本篇博客的主角。简单直白说就是每次拍摄曝光较短时间，但连续曝光拍摄多张，最后再利用软件合成一张完整的星轨。这种方法的好处是每次曝光时间都较短，这样拍摄出来的照片不会像一次超长曝光那样很亮，可以保持在相对正常的范围。而它的坏处就是多张照片合成时，控制不好后期星轨容易出现一段一段的类似虚线的情况。对于这一情况网上给的减轻方法是关闭相机的自动降噪功能。
而关于每次到底曝光多长时间，则根据你的实际需求了，但不应该小于600法则所计算的最短时间，否则星星形成不了轨迹。所谓600法则是指600除以拍摄相机镜头的焦距，获得的这个值就是这个镜头拍摄星星不拖影的最长曝光时间。换句话说也就是拖影的最短时间。例如我拍摄时镜头焦距是15mm，佳能APS-C画幅，等效系数是1.6，所以等效焦距是24mm，用600除以24是25s。也就是说我这个镜头要想拍摄星轨，单次曝光时间不应小于25s。在实际拍摄时我设置的是120s。
在利用相机拍摄完照片后，自然迫不及待的想要合成看看效果了。星轨合成软件比较常用的有德国的Startrails等等，当然PS都是可以的。作为一个会点CV的“码农”，对于这种相关的需求自然想自己写代码试试看了。所以本篇博客主要从技术上研究探讨下如何实现星轨堆栈叠加以及遇到的问题。
1.叠加原理与算法
从CV角度来说，叠加的思路其实相对简单，基本都是在像素级的运算与操作。最初的想法是所有相片灰度值相加再取平均，这有点类似于之前说的利用平均值法提取背景。但这样对于星轨合成是不合适的。因为星星本身在运动，星轨的拍摄是一段一段的，并不是累加。所以这样做就会出现最后部分很亮，之前的就被多次平均给“抹去”了。
因此不能取平均，就采用其它办法。由于拍摄的照片间基本是严格对齐的，所以可以对每一个像素位置的灰度值进行比较，选择一个作为最终的结果。由于星轨相比于夜空灰度差异是比较明显的，因此很容易区分出来。这里有不同的比较方式，如选择最大值、阈值判断等等。最后输出影像即可得到合成后的星轨。举例来说，如拍摄了10张照片，程序会逐像素遍历影像，如对于(100,100)位置，把这10张影像的当前位置灰度全部取出来，找到最大灰度，将最大灰度赋给合成影像的对应位置即可，这便是最大值法。
2.叠加代码
# coding=utf-8
import cv2
import numpy as np
from numba import jit
import os
from collections import Counter
import time
def findAllFiles(root_dir, filter):
"""
在指定目录查找指定类型文件
:param root_dir: 查找目录
:param filter: 文件类型
:return: 路径、名称、文件全路径
"""
print("Finding files ends with \'" + filter + "\' ...")
separator = os.path.sep
paths = []
names = []
files = []
for parent, dirname, filenames in os.walk(root_dir):
for filename in filenames:
if filename.endswith(filter):
paths.append(parent + separator)
names.append(filename)
for i in range(paths.__len__()):
files.append(paths[i] + names[i])
print (names.__len__().__str__() + " files have been found.")
paths.sort()
names.sort()
files.sort()
return paths, names, files
def joinPairwiseTh(img1, img2, diffTh=10):
join_img = img1.copy()
img1_gray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
img2_gray = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
diff = img2_gray.astype(np.int) - img1_gray.astype(np.int)
diff_pixels = np.argwhere(diff > diffTh)
for i in range(diff_pixels.__len__()):
join_img[diff_pixels[i][0], diff_pixels[i][1]] = img2[diff_pixels[i][0], diff_pixels[i][1]]
return join_img
def joinPairwiseMax(img1, img2):
join_img = img1.copy()
img1_gray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
img2_gray = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
diff = img2_gray.astype(np.int) - img1_gray.astype(np.int)
diff_pixels = np.argwhere(diff >= 0)
for i in range(diff_pixels.__len__()):
join_img[diff_pixels[i][0], diff_pixels[i][1]] = img2[diff_pixels[i][0], diff_pixels[i][1]]
return join_img
def joinPairwiseMin(img1, img2):
join_img = img1.copy()
img1_gray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
img2_gray = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
diff = img2_gray.astype(np.int) - img1_gray.astype(np.int)
diff_pixels = np.argwhere(diff <= 0)
for i in range(diff_pixels.__len__()):
join_img[diff_pixels[i][0], diff_pixels[i][1]] = img2[diff_pixels[i][0], diff_pixels[i][1]]
return join_img
@jit(nopython=True)
def joinPairwiseMean(img1, img2):
join_img = img1.copy()
for i in range(img1.shape[0]):
for j in range(img2.shape[1]):
mean_b = (img1[i, j, 0] + img2[i, j, 0]) / 2
mean_g = (img1[i, j, 1] + img2[i, j, 1]) / 2
mean_r = (img1[i, j, 2] + img2[i, j, 2]) / 2
join_img[i, j] = [mean_b, mean_g, mean_r]
return join_img
def joinBatch(imgs, method='max', diffTh=10):
print "Initializing ..."
img1 = cv2.imread(imgs[0])
img2 = cv2.imread(imgs[1])
if method is 'max':
print "starting using max method for pixel fusion..."
join = joinPairwiseMax(img1, img2)
for i in range(2, imgs.__len__()):
print i + 1, "/", imgs.__len__()
tmp_img = cv2.imread(imgs[i])
join = joinPairwiseMax(join, tmp_img)
elif method is 'min':
print "starting using min method for pixel fusion..."
join = joinPairwiseMin(img1, img2)
for i in range(2, imgs.__len__()):
print i + 1, "/", imgs.__len__()
tmp_img = cv2.imread(imgs[i])
join = joinPairwiseMin(join, tmp_img)
elif method is 'mean':
print "starting using mean method for pixel fusion..."
join = joinPairwiseMean(img1, img2)
for i in range(2, imgs.__len__()):
print i + 1, "/", imgs.__len__()
tmp_img = cv2.imread(imgs[i])
join = joinPairwiseMean(join, tmp_img)
elif method is 'th':
print "starting using threshold method for pixel fusion..."
join = joinPairwiseTh(img1, img2, diffTh=diffTh)
for i in range(2, imgs.__len__()):
print i + 1, "/", imgs.__len__()
tmp_img = cv2.imread(imgs[i])
join = joinPairwiseTh(join, tmp_img, diffTh=diffTh)
print "star trail join finished!"
return join
在实现中，有一些小技巧，例如由于拍摄的原图都很大，所以最好不要一下将所有影像都一次性读到内存里来，这样很容易造成内存使用过多死机。比较稳健的办法是两两合成，也即每次合成只读一张影像到内存里来，与当前结果进行运算(取最大值或其它算法等等)，这样内存的压力会小很多。
最后，对之前拍摄的30张照片进行了合成，效果如下。
总体而言效果还是不错的。如果放大看星轨有一断一断的感觉(如果用原图合成更明显)，这便是上面提到过的问题。最后，将代码和拍摄的测试照片(由于原始照片太大所以进行了压缩，如果需要原图可以自己拍或者联系我)都传到了Github，项目叫AutoStartrailGenerator，点击查看。
3.继续改进
当然这个代码还是有很多问题的。首先就是“断线”问题。应该可以用一些图像生长算法解决，有空再研究下。另一个是取最大值这个算法会导致最后合成的影像整体偏亮，但其实我们希望的最好状态是星轨和星空部分亮一些、一些无关紧要的地物尽量暗一些。因此可以运用一些算法识别出地物和星空，对不同部分采用不同算法。对于星空采用取最大值的办法，对于地物采用取最小值或者均值的办法，尽量降低地物亮度。在代码中也对这个想法进行了尝试。
如何区分地物和星空，想法是利用影像的二维熵，关于什么是信息熵可以看这篇博客。简单来说某个图像其熵越大，表示影像纹理信息越丰富。基于这个特性，首先在影像中，对每一个像素的局部小窗口都计算一个熵，作为该像素的熵值，然后取所有像素熵值的平均(或其它算法)作为分割阈值。若其大于均值，则认为该像素是地物，标记为1，若小于均值，则认为是星空，标记为0。这样即可以获得一个二分的mask。再逐像素遍历影像，对不同类型像素采用不同方法即可。对于本想法也实现了，代码如下。
# coding=utf-8
import cv2
import numpy as np
from numba import jit
import os
from collections import Counter
import time
def calcIJ(img_patch):
total_p = img_patch.shape[0] * img_patch.shape[1]
center_p = img_patch[img_patch.shape[0] / 2, img_patch.shape[1] / 2]
mean_p = (np.sum(img_patch) - center_p) / (total_p - 1)
return (center_p, mean_p)
def calcEntropy2d(img, win_w=3, win_h=3):
ext_x = win_w / 2
ext_y = win_h / 2
# 考虑滑动窗口大小，对原图进行扩边
final_img = cv2.copyMakeBorder(img, ext_y, ext_y, ext_x, ext_x, cv2.BORDER_REFLECT)
new_width = final_img.shape[1]
new_height = final_img.shape[0]
# 依次获取每个滑动窗口的内容
IJ = []
for i in range(img.shape[0] - win_w):
for j in range(img.shape[1] - win_h):
patch = final_img[i + ext_x:i + ext_x + win_w + 1, j + ext_y:j + ext_y + win_h + 1]
IJ.append(calcIJ(patch))
# 循环遍历统计各二元组个数
Fij = Counter(IJ).items()
# 计算各二元组出现的概率
Pij = []
for item in Fij:
Pij.append(item[1] * 1.0 / (new_height * new_width))
# 计算每个概率所对应的二维熵
H_tem = []
for item in Pij:
h_tem = -item * (np.log(item) / np.log(2))
H_tem.append(h_tem)
# 对所有二维熵求和
H = sum(H_tem)
return H
def getEntropyMap(img, big_win_w=7, big_win_h=7, small_win_w=3, small_win_h=3):
if img.shape.__len__() == 3:
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ext_x = big_win_w / 2
ext_y = big_win_h / 2
final_img = cv2.copyMakeBorder(img, ext_y, ext_y, ext_x, ext_x, cv2.BORDER_REFLECT)
entropy_img = np.zeros([img.shape[0], img.shape[1]], np.float)
# 依次获取每个滑动窗口的内容
total_pixel = img.shape[0] * img.shape[1]
counter = 0
times = []
step = 10000
for i in range(img.shape[0] - big_win_h):
for j in range(img.shape[1] - big_win_w):
patch = final_img[i + ext_x:i + ext_x + big_win_w + 1, j + ext_y:j + ext_y + big_win_h + 1]
entropy = calcEntropy2d(patch, win_w=small_win_w, win_h=small_win_h)
entropy_img[i, j] = entropy
counter += 1
if counter % step == 0:
if times.__len__() == 0:
times.append(time.time())
print round((counter * 1.0 / total_pixel) * 100, 2), "% finished"
else:
times.append(time.time())
dt = times[-1] - times[-2]
remain_time = round(((total_pixel - counter) / step) * dt)
print round((counter * 1.0 / total_pixel) * 100), "% finished,", \
"remain time:", remain_time, "s"
print "100% finished"
mean_entropy = np.mean(entropy_img)
entropy_img = np.where(entropy_img == 0, mean_entropy, entropy_img)
return entropy_img
def getEntropyThreshold(entropy_img, methold='mean'):
if methold == 'mean':
mean_entropy = np.mean(entropy_img)
print "mean", mean_entropy * 1.2
return mean_entropy
elif methold == 'stat':
# 确定合适阈值
max_val = np.max(entropy_img)
min_val = np.min(entropy_img)
print "max", max_val
print "min", min_val
step_length = (max_val - min_val) / 10
bin = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for i in range(entropy_img.shape[0]):
for j in range(entropy_img.shape[1]):
corresponding_index = int((entropy_img[i, j] - min_val) / step_length)
bin[corresponding_index] += 1
r1 = bin.index(max(bin))
threshold = (r1 + 1) * step_length
return threshold
def getEntropyMask(entropy_img, th):
mask = np.where(entropy_img > th, 1, 0)
return mask
def joinPairwiseEntropy(img1, img2, entropy_mask):
join_img = img1.copy()
img1_gray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
img2_gray = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
for i in range(entropy_mask.shape[0]):
for j in range(entropy_mask.shape[1]):
if entropy_mask[i, j] == 1:
# 对于非地物，取最小值
if img2_gray[i, j] < img1_gray[i, j]:
join_img[i, j] = img2[i, j]
else:
# 对于星空，取最大值
if img2_gray[i, j] > img1_gray[i, j]:
join_img[i, j] = img2[i, j]
return join_img
def joinBatchEntropy(imgs, entropy_reference=0):
print "Initializing ..."
img1 = cv2.imread(imgs[0])
img2 = cv2.imread(imgs[1])
entropy_img = getEntropyMap(cv2.imread(imgs[entropy_reference]))
entropy_th = getEntropyThreshold(entropy_img, methold='mean')
mask = getEntropyMask(entropy_img, entropy_th)
print "starting using entropy method for pixel fusion..."
join = joinPairwiseEntropy(img1, img2, mask)
for i in range(2, imgs.__len__()):
print i + 1, "/", imgs.__len__()
tmp_img = cv2.imread(imgs[i])
join = joinPairwiseEntropy(join, tmp_img, mask)
return join
代码对于一个1200×800的影像计算一次二维熵大约需要约3分多钟的时间，效率还有待提高。
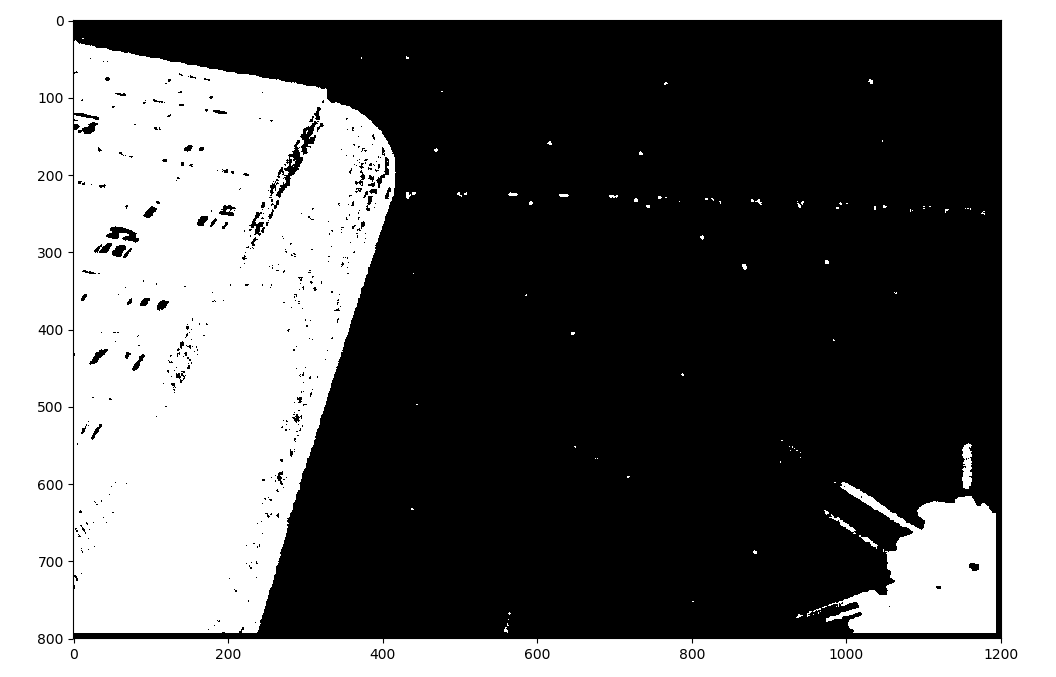
计算出的二维熵图如下所示，大体而言可以区分的出地物和天空。程序计算出的平均熵值是1.34。
基于二维熵图利用平均值方法进行阈值分割后获得的掩膜如下所示。
测试的局部对比效果如下。左边是采用信息熵分类后的混合结果，右边是采用最大值算法直接混合的结果。
可以发现有较多斑点，这主要是因为分割的模板不够准确导致的。在人为提高阈值到1.4以后，斑点情况有改善，如下对比所示。
以及阈值为1.4时对应的掩膜，可以看到相比于平均值，星空的噪点少了很多。
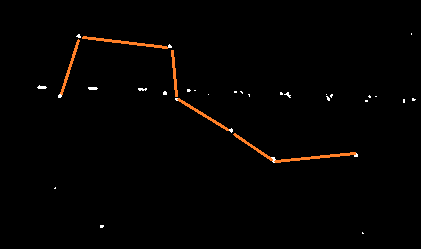
其实如果仔细观察就会发现，其实星空上的噪点就是一些比较亮的星星。例如在上面的掩膜中，可以很容易的找到北斗七星，如下图所示。
与最大值法相比，信息熵的方法地物部分相对暗一些，基本符合我们之前的预期。但这个算法的一个很大的缺点就是计算量较大，图像稍微大一些就比较慢，这里只是给出一个思路。此外还有如何准确选择分割阈值问题等等需要解决，虽然提取的地物相比于最大值法要暗一些，但因为没有使用更复杂的阈值提取算法，但是导致存在很多“噪点”。因此也还有继续改进的空间，如采用GPU加速、尝试Otsu二值化方法进行合理分割、对影像进行平滑预处理去除噪声、获得掩膜后对掩膜进行腐蚀操作去除零星噪点等方法。关于Python如何使用GPU加速可以参考这篇博客。
本文作者原创,未经许可不得转载,谢谢配合
