本篇博客主要介绍传统计算机视觉领域里一个被用于纹理分析的工具——灰度共生矩阵。
1.什么是灰度共生矩阵
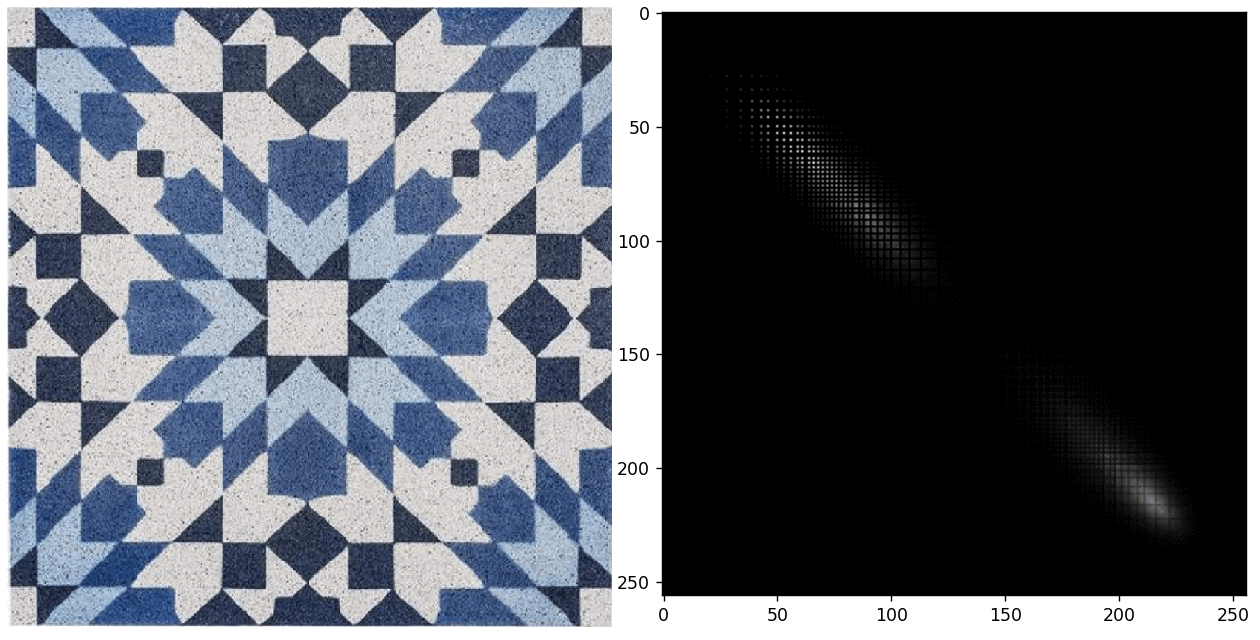
灰度共生矩阵英文为Gray-level Co-occurrence Matrix, GLCM。其在1973年由Haralick等人提出。当时提出灰度共生矩阵最主要的目的就是描述纹理特征。由于纹理是由灰度分布在空间位置上反复出现而形成的,因而在图像空间中相隔某距离的两像素之间会存在一定的灰度关系,即图像中灰度的空间相关特性。灰度共生矩阵就是用来描述这种空间相关性的,这也是“共生”这个词的意义。灰度共生矩阵描述的从来不是单个像素,而是成对的像素之间的关系(对应的,灰度直方图则可以看做是对单个像素的统计与描述,并不涉及灰度间的关联关系)。如下图所示,为一幅普通的图片以及对应的灰度共生矩阵。

2.灰度共生矩阵如何计算
2.1 计算原则
把两个灰度级的数值作为灰度共生矩阵的位置,把这种模式出现的次数作为灰度共生矩阵中该位置的数值。
前面说了灰度共生矩阵用于描述灰度的空间关系。具体如何计算呢?也非常简单。首先我们想,对于一个包含256个灰度级的8bit影像,两个灰度级a、b之间的关系(a,b)可以有256×256种。这里我们认为(1,2)和(2,1)是两种关系。因此,我们不妨以灰度级a、b作为两个维度,这样就可以组成一个二维矩阵,它包含256行、256列。所以从这个角度可以看出,灰度共生矩阵一定是个方阵,只是由于量化级数的不同,会有不同的尺寸。 这个矩阵就是我们研究的灰度共生矩阵。矩阵的框架搭好了,里面的元素怎么算呢?
很简单。在灰度矩阵中,我们随意取出某个位置(i,j),它表示的就是灰度级i和灰度级j的关联。如何定义这种关联呢?我们不妨统计这种关联模式出现的次数,出现的次数越多表示关联越强。因此,我们遍历原图,如果出现了i和j相邻的情况,那么灰度共生矩阵中(i,j)位置的元素就加一。这样,我们就能找到所有像素灰度级之间的关系,进而填充整个灰度共生矩阵。
当然细心的你这时可能会有疑问。上面说的这些还是不够具体。如何定义灰度级i和j相邻呢?事实上,不同的定义方式就会有不同的灰度共生矩阵计算方法。比如,我们可以定义为水平方向。这样在遍历图像的时候,我们依次取出水平方向的两个像素灰度进行判断(这样我们研究的就相当于是整幅图像中水平方向上的灰度关联关系)。当然也可以定义为竖直方向,甚至是45、135方向。而且这种比较也涉及到步长问题,以水平方向为例,如果步长为1,那么就表示比较相邻的(i,j)和(i,j+1)像素。
最后,我们就可以获得所有灰度关联模式在原图中的出现的个数。我们对其进行求和,然后让每个元素除以总次数,这样得到的就是某个关联模式出现的概率。
2.2 简单实现
基于以上的原则,我们可以十分方便的用Python进行实现,这里我们只简单实现了水平方向灰度共生矩阵的计算(这里没有归一化,所以和归一化后的矩阵差个倍数关系),实现代码如下。
# coding=utf-8
import cv2
import numpy as np
from matplotlib import pyplot as plt
if __name__ == '__main__':
step = 1
img_path = "img1.png"
img = cv2.imread(img_path, cv2.IMREAD_GRAYSCALE)
img_width = img.shape[1]
img_height = img.shape[0]
print(img_width, img_height)
glcm = np.zeros([256, 256])
for i in range(0, img_width - step, step):
for j in range(img_height):
pos_x = img[j, i]
pos_y = img[j, i + 1]
glcm[pos_x, pos_y] = glcm[pos_x, pos_y] + 1
total_num = np.sum(glcm)
print(total_num)
grayscale_x = []
grayscale_bins = []
counter = 0
for i in range(256):
grayscale_x.append(counter)
grayscale_bins.append(np.sum(glcm[i, :]))
counter += 1
plt.bar(grayscale_x, grayscale_bins)
plt.show()
plt.imshow(glcm, cmap='gray')
plt.show()
如下图所示,为利用上面的代码绘制出的灰度共生矩阵。
3.灰度共生矩阵的特征
3.1 对矩阵的分析
上面我们简单计算了灰度共生矩阵的计算方法以及具体的实现代码。在这一部分,我们则重点分析一下,灰度共生矩阵所代表的含义。下面就简单分析。
首先,前面也分析了,灰度共生矩阵是一个二维方阵,其维度等于影像的灰度量化级数,如256等。其次,你会发现灰度共生矩阵和灰度直方图是类似的,也是对灰度进行统计,只不过统计的并不是灰度数值,而是不同灰度级之间的关系。或者其实可以理解为是一种“二维”的灰度直方图或者是协方差矩阵。
那么灰度共生矩阵中的每一行或者每一列代表什么呢?这里以行为例。比如第一行,它表示的就是所有(0,x)关系的出现次数。如果将它们累加起来,它表示的就是原图中所有灰度为0的出现次数。如果我们对每一行都进行累加,就可以得到一个256维的向量。对于其中第i维的值n,其就是表示在原图中,灰度级为i的像素一共出现了n次。如果你比较敏感的话,立马就能反应过来,这就是灰度直方图。所以我们前面说,灰度共生矩阵像是一种“二维”的灰度直方图就在于这里。在某些特定情况下,我们可以根据灰度共生矩阵推导出灰度直方图。
当然这里其实是一种“近似”。因为我们虽然遍历了影像,但并没有进行影像总像素个数次比较。举个例子,比如原图为600×400,那么共有240000个像素。我们以水平方向计算关联关系,步长设为1,那么每一行我们其实会进行599次对比,400行共有599×400次,也就是239600次。这样的结果就是,我们如果在灰度共生矩阵中统计个数,最终其实会少统计400个像素。所以说,这其实是一种“近似”的灰度直方图。
另一个问题是矩阵的对角线有什么特殊含义?根据灰度共生矩阵的定义,对角线元素表示的是灰度级i和灰度级i相邻这种模式出现的次数。如果放到图像上来看也就是说相邻的两个像素灰度没有变化。所以,如果对角线非零元素集中于某一区域,则说明影像中存在较多同灰度的纯色色块;而如果对角线非零元素分布相对均匀,则说明影像中存在较多不同灰度等级的纯色色块。
还有一个问题,那就是,灰度共生矩阵中,如果所有元素求和,有什么意义?其实和上面介绍的类似。所有元素求和,等于原图总像素个数减去步长并乘以跳跃的次数。
最后一个问题,灰度共生矩阵是对称的吗?答案是不一定。因为,在定义中,(1,3)和(3,1)表示的是两种不同的灰度关系。所以完全有可能出现(1,3)有100个,而(3,1)只有10个的情况。
3.2 矩阵的特性
灰度共生矩阵作为一种特殊的矩阵,当然也有一些可以统计的特性,这里简单列举如下。
3.2.1 对比度
对比度用于度量矩阵值的分布和局部变化,反应图像的清晰度和纹理的沟纹深浅。对比度越大,影像越清晰。计算公式为:
\[Con = \sum_{i}^{} \sum_{j}^{} (i-j)^{2}P(i,j)\]其中,i、j为共生矩阵中的坐标索引,P(i,j)为该位置的灰度值(对于共生矩阵来说就是某种灰度关联关系出现的次数)。
3.2.2 能量
灰度共生矩阵元素值的平方和,称其为能量,也叫第二角力矩(Angular Second Moment, ASM)。反应了图像灰度分布均匀程度和纹理粗细度。如果其较大,则表明图像中存在一种较为均一和规则变化的纹理模式。计算公式如下。
\[Asm = \sum_{i}^{} \sum_{j}^{} P(i,j)^{2}\]3.2.3 熵
熵的概念和计算在之前这篇博客和这篇博客中介绍过。在灰度共生矩阵中表示图像的信息量。当共生矩阵中元素分布较为分散时,熵较大。它表示了图像中纹理的非均匀程度或者复杂程度。计算公式如下。
\[Ent = \sum_{i}^{} \sum_{j}^{} P(i,j)logP(i,j)\]3.2.4 相关度
度量灰度共生矩阵元素在行或列方向上的相似程度(Inverse Different Moment)。其值反应了图像中局部灰度相关性。当矩阵元素均匀相等时,相关度较大,反之较小。计算公式如下。
\[IDM = \sum_{i}^{} \sum_{j}^{} \frac{P(i,j)}{1+(i-j)^{2}}\]4.灰度共生矩阵有什么作用
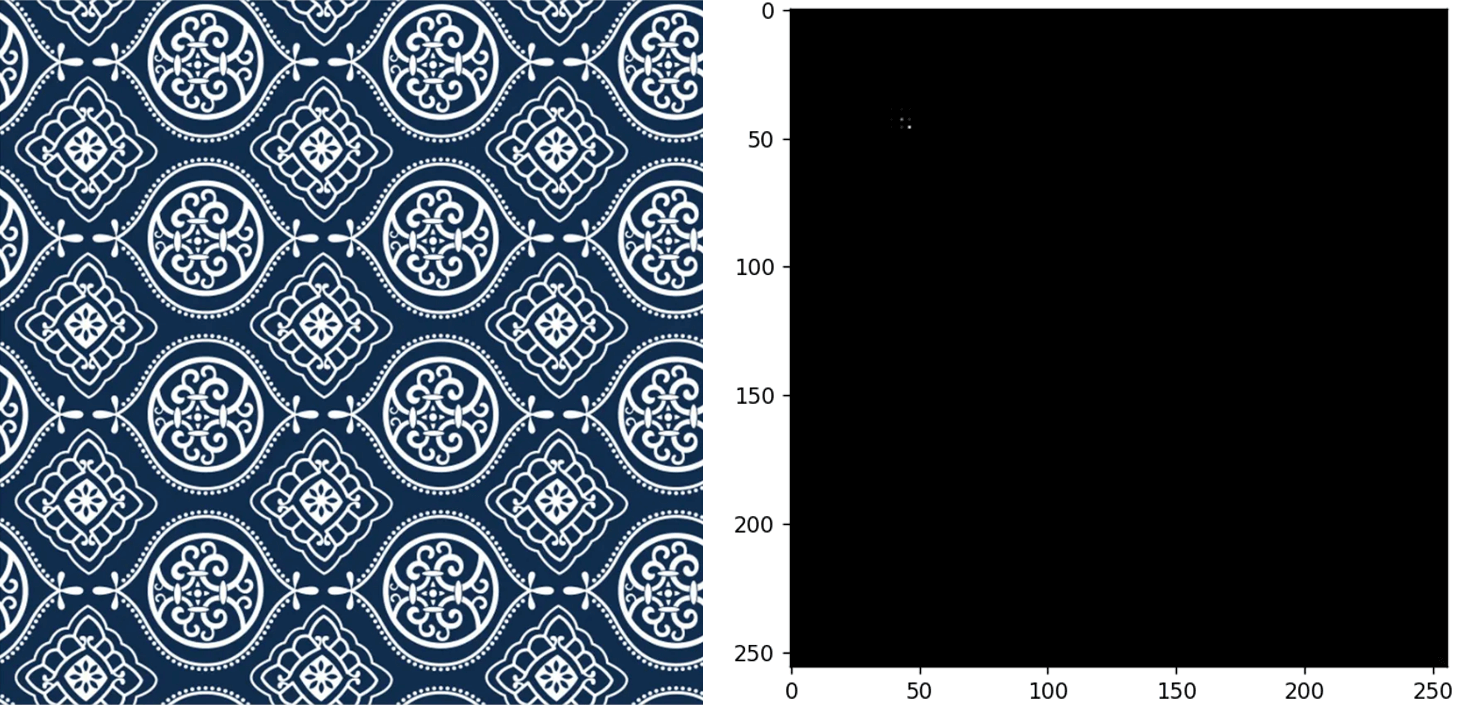
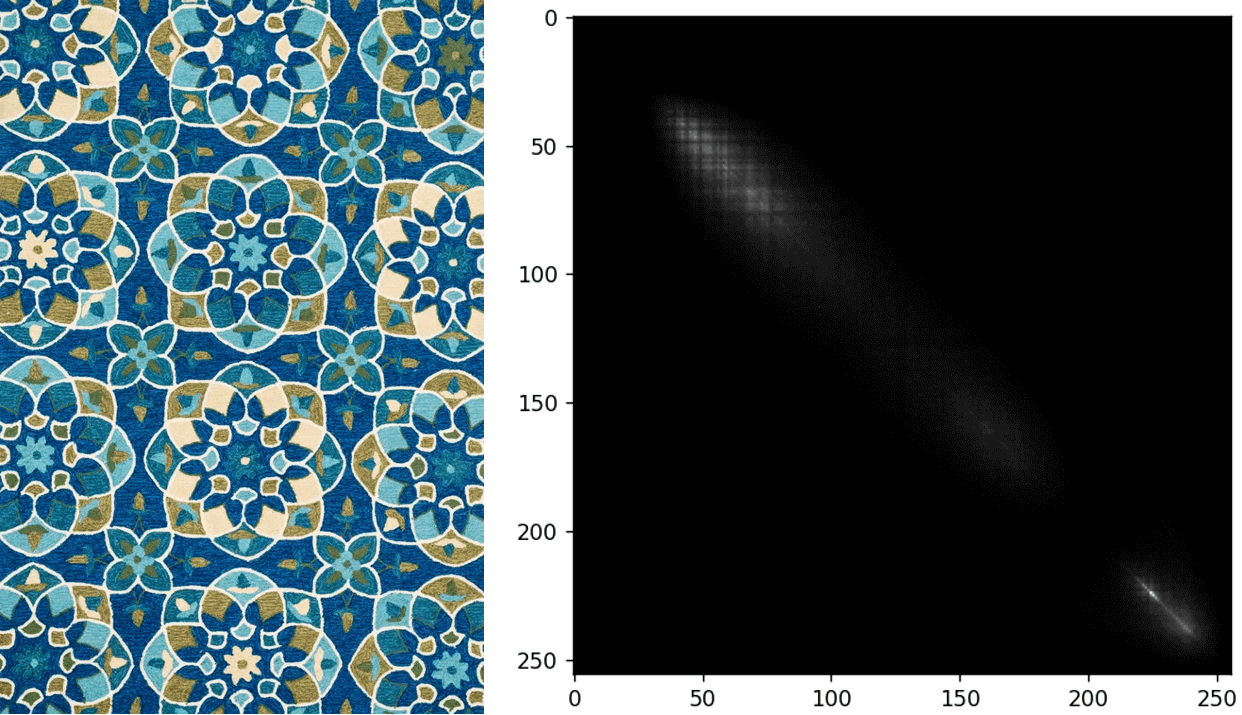
可以用来找一些影像中有重复的纹理信息。如果灰度共生矩阵集中于某一区域,那么说明这个影像的纹理信息较为单一,否则则较为复杂。如下图所示,为两张图像以及对应的灰度共生矩阵。
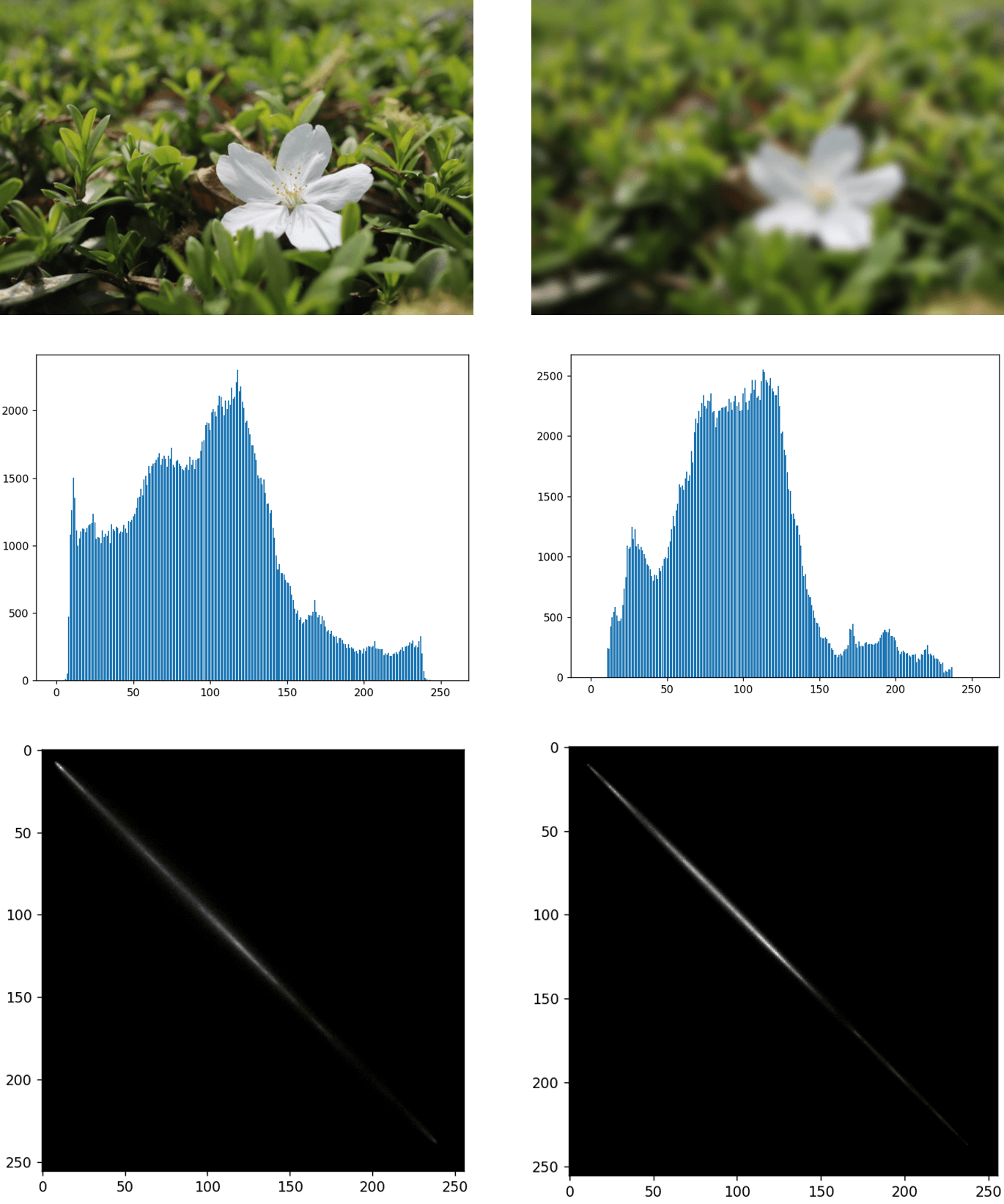 可以看到,在模糊的影像上,灰度共生矩阵分布的更为集中,这也就表示,灰度级的关联关系变得更加单一了(因为一些灰度变化的细节被模糊掉了)。此外,也找了一些比较好看的纹理,计算了对应的灰度共生矩阵,如下。
可以看到,在模糊的影像上,灰度共生矩阵分布的更为集中,这也就表示,灰度级的关联关系变得更加单一了(因为一些灰度变化的细节被模糊掉了)。此外,也找了一些比较好看的纹理,计算了对应的灰度共生矩阵,如下。
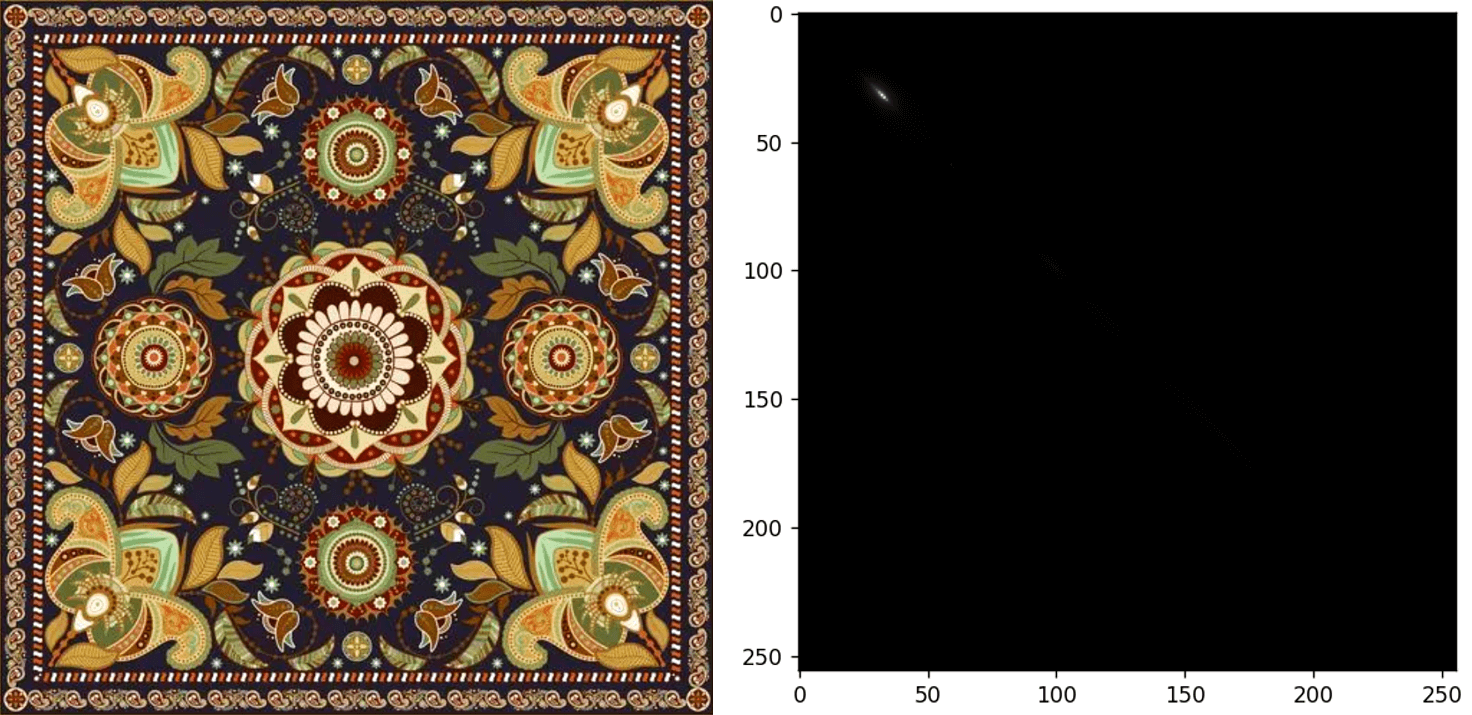
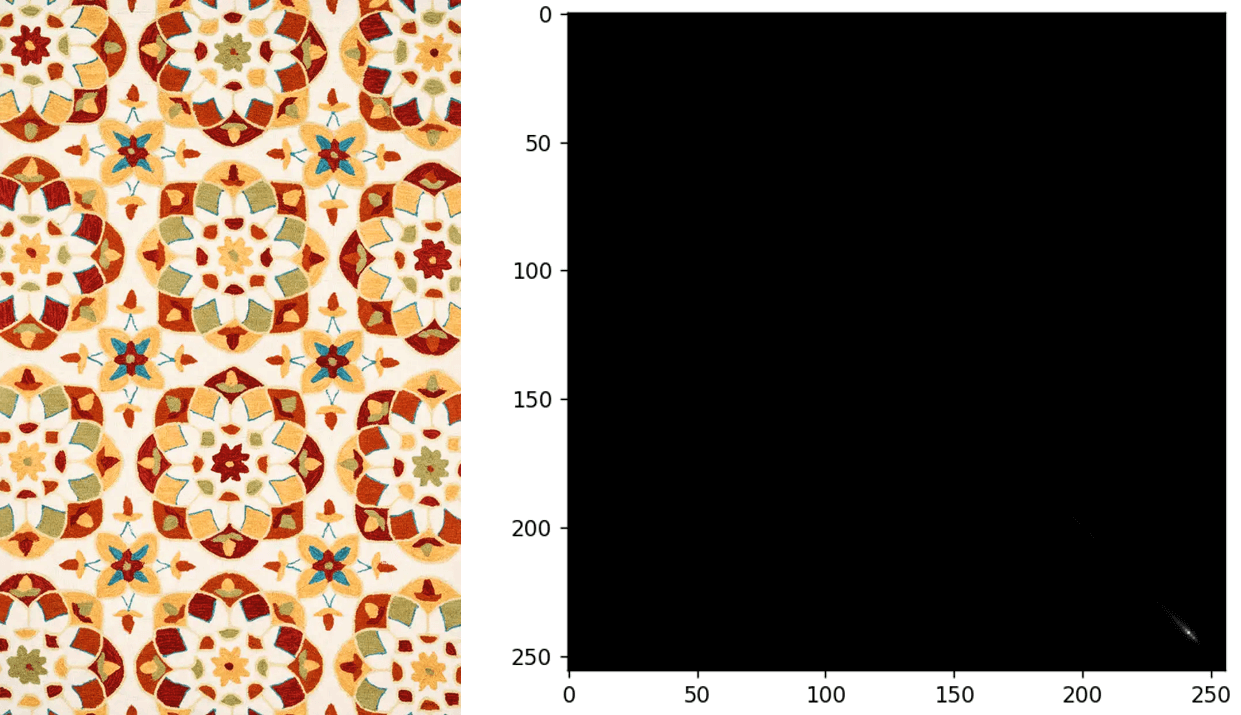
5.参考资料
- [1] https://blog.csdn.net/guanyuqiu/article/details/53117507
- [2] https://zhuanlan.zhihu.com/p/367213524
- [3] https://zhuanlan.zhihu.com/p/295444415
- [4] https://www.cnblogs.com/lq123/p/13394271.html
- [5] https://www.cnblogs.com/sddai/p/11431783.html
- [6] https://blog.csdn.net/guanyuqiu/article/details/53117507
本文作者原创,未经许可不得转载,谢谢配合
