- 1.Vanishing Points-How to Compute Camera Orientation
- 2.Compute Projective Transformations
- 3.Projective Transformations and Vanishing Points
- 4.Cross Ratios and Single View Metrology
- 5.Two View Metrology
1.Vanishing Points-How to Compute Camera Orientation
将一个三维点转换到像素的过程有两个关键因素：一是相机拍摄时的R和t(外参)，二是相机的内参矩阵K。
灭点与旋转的关系
简单的一维情况：
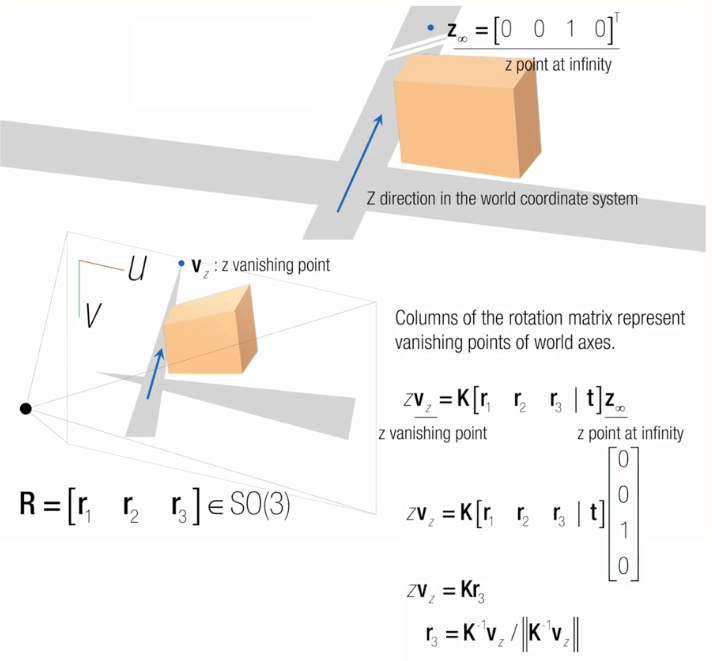如图像面上z方向的灭点在真实世界中的坐标可以记为(0,0,1)，为了表示这个点在无限远处，在最后加个0，变为(0,0,1,0)。而将这个点带入成像方程里，3×4的相机变换矩阵(外参矩阵)与4×1的点坐标相乘，只剩下3×1的r3。所以K逆乘以z·Vz(将像素坐标转换到光学世界)即可以得到r3，这里的已知量是Vz和K，待求量是r3，但式子中还有一个尺度因子z。但其实有没有z对最终结果没有任何影响。因为r3是旋转矩阵中的一列，所以它的模应该为1，也就是说最后要对其进行归一化，这就等于是消除了z的影响。举个简单的例子向量(1,2,3)和向量(2,4,6)最终归一化后的向量是一样的。
旋转矩阵列向量所代表的物理意义：
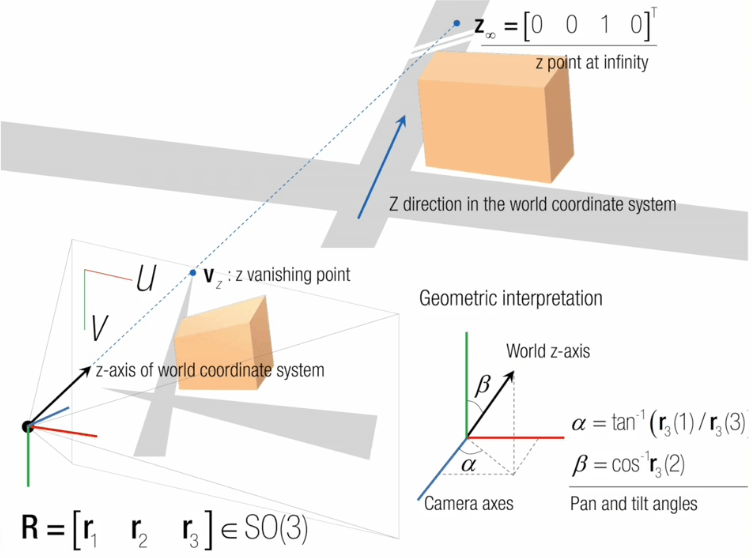在这里表示世界坐标系的z轴在相机坐标系下的旋转角度，对应实际的pan和tilt角度。需要注意的是只使用一个z方向上的灭点只能恢复出pan和tilt，对于roll无法恢复。因为绕z轴旋转z轴灭点在图像上的位置是不会改变的。后面会说到，给定两个互相垂直方向上的灭点，即可以完整恢复相机的相对姿态。
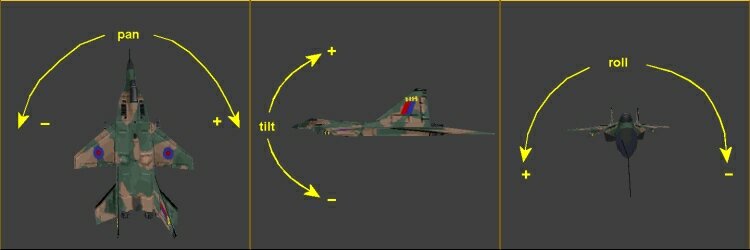
对于三维旋转的表示，pan表示绕z轴(不是相机坐标系的z轴)旋转(0-360)，对应yaw；tilt表示绕y轴(不是相机坐标系的y轴)旋转(-90 - 90)，对应pitch；roll表示绕x轴(不是相机坐标系的x轴)旋转(0-360)，示意图如下。更详细的介绍参考这个网页。
二维情况：
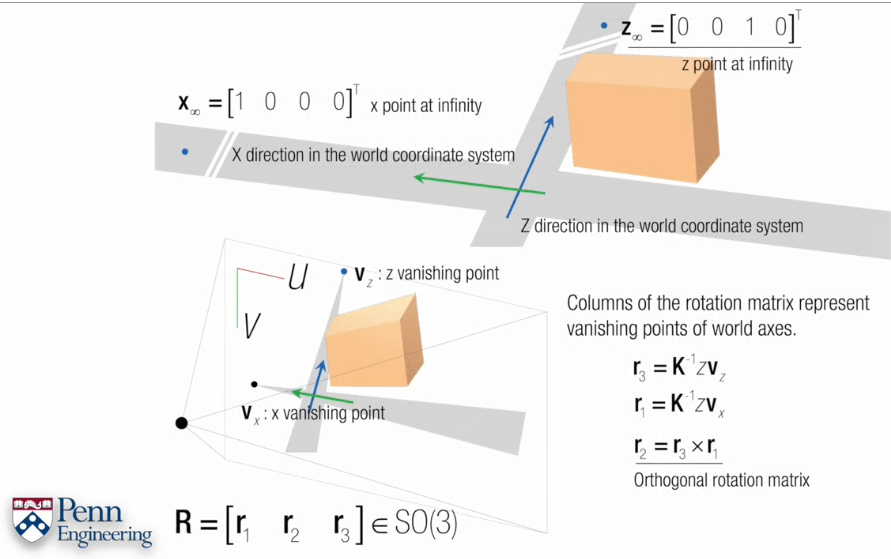与z方向类似，x方向上的灭点在真实世界中的坐标可记为(1,0,0)，为了表示无限远，在最后加个0,变为(1,0,0,0)。r1解法与r3一样，在求得r3和r1后(别忘了归一化)，r2可以由r3叉乘r1得到(因为旋转矩阵的正交性，各分量间互相垂直)。得到r1、r2、r3以后，将它们组成矩阵即为旋转矩阵R，表示相机相对于世界的旋转。
这里需要注意的一点是r2的叉乘顺序问题，是r3×r1还是r1×r3，它们的差别在于最后得到的结果方向相反。顺序准则是最后叉乘得到的方向和现有方向要满足右手定则。如下图所示坐标系中：
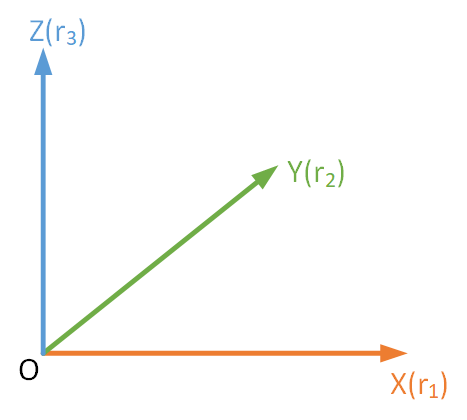根据右手定则可以很容易地得到：r3=r1×r2、r2=r3×r1、r1=r2×r3。再补充一点：两个单位正交向量叉乘，结果还是单位向量。
因此也可以看出来，要想利用灭点恢复相机姿态，至少需要找到两个互相垂直方向上的灭点。
一些例子：
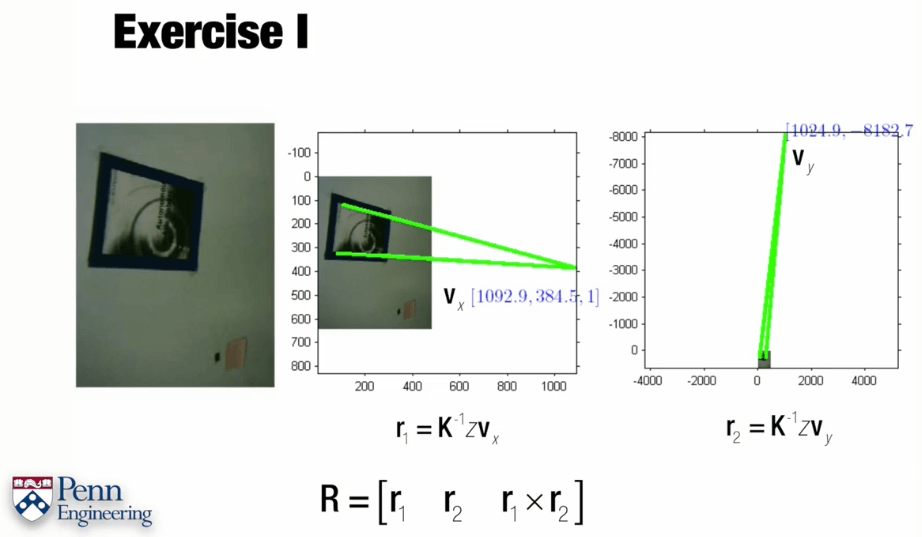
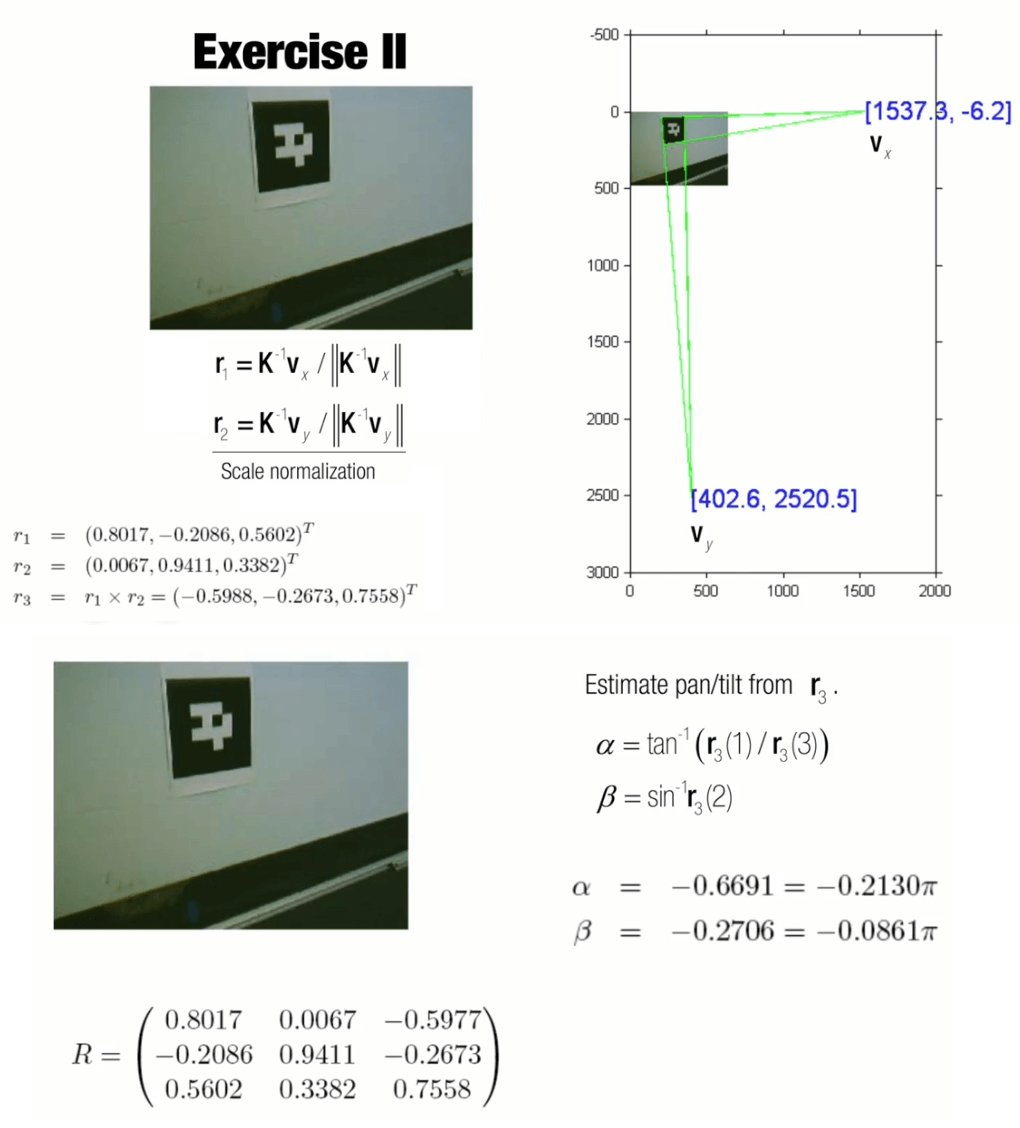
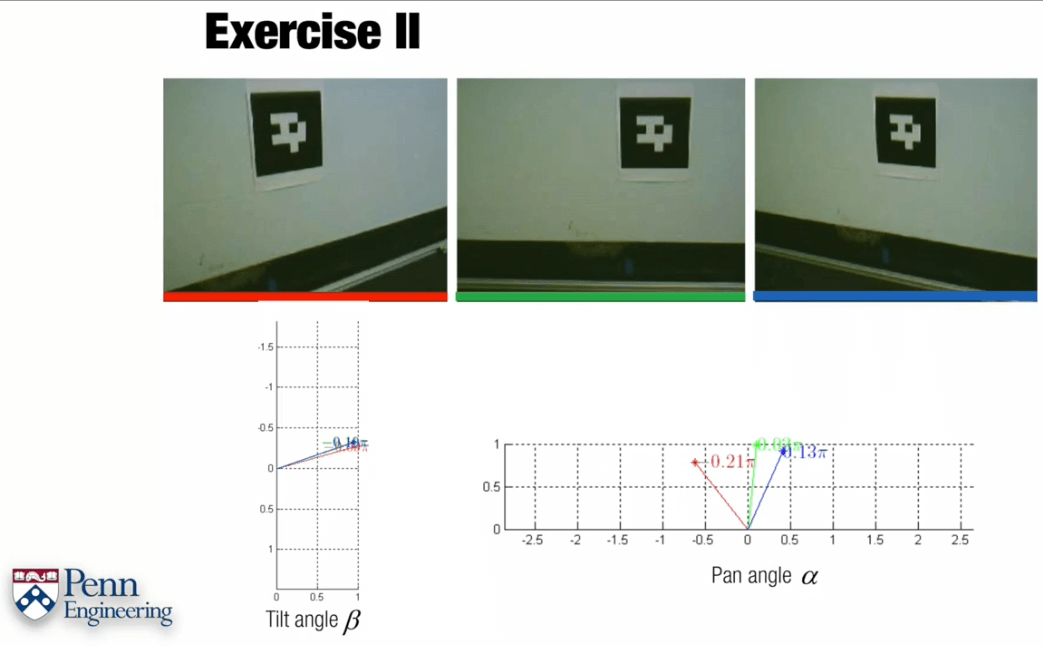由以上例子可以看出，要想用灭点求姿态，需要在图片中找到两组现实世界中互相垂直方向上的平行线，然后利用齐次坐标(坐标增加一维1)随意表示线上两点，利用叉乘求得直线方程，再将两个直线做叉乘，即可得到它们的交点(要把向量同除以z，使z分量化为1才表示在像面上的交点坐标)。这样两组平行线就可以得到两个交点如Vx和Vy，这样再结合内参矩阵K，就可以求得r1、r2，进而r3=r1×r2，得到r1、r2、r3以后别忘了分别对它们归一化，最终可获得相对于那个物体的旋转矩阵R。We can orientate ourself respect to that object.
平面情况下的单应变换
上面介绍的利用真实世界中两个垂直方向上灭点计算相机相对旋转的办法无法恢复平移t。要想同时恢复旋转和平移，应该使用单应变换(Homography transformation)，从一个3D坐标中的平面到2D坐标下的平面。
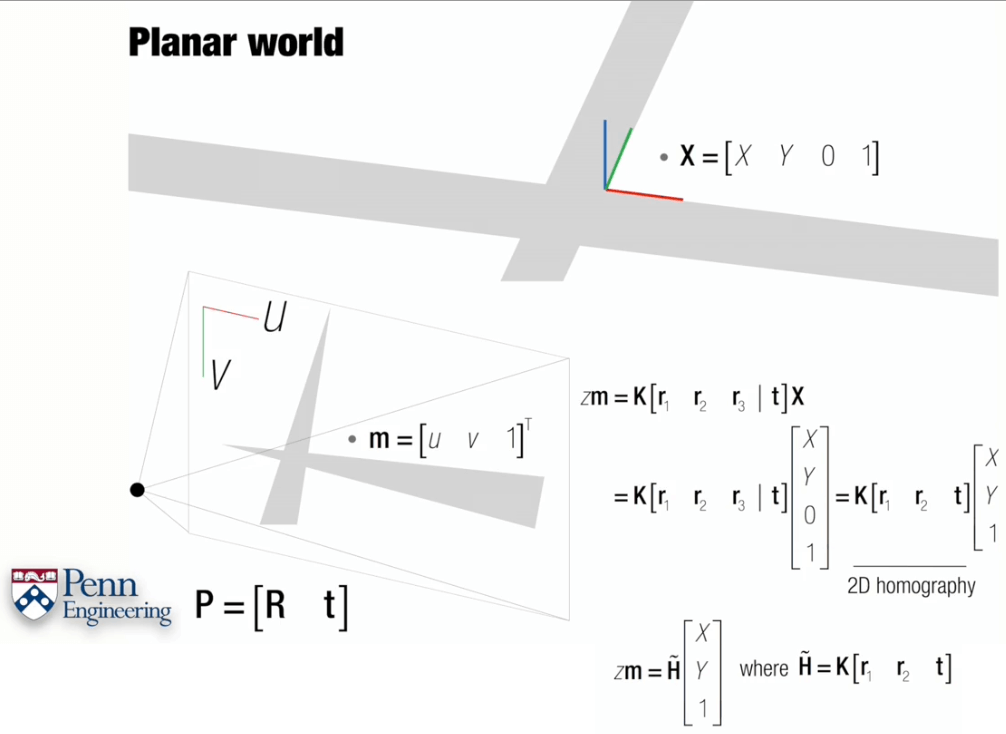假设地面(x-y平面)上有一个点，那么它用齐次坐标表示就是(X,Y,0,1)，通过变换得到在像面上的像素坐标为m(u,v,1)。在将坐标与变换矩阵相乘时，很明显r3就会被消掉。这样，把K以及r1、r2、t相乘组成的矩阵叫做H，即为单应矩阵，它可以由至少4个点利用数值算法求出。注意这里的r1、r2模长为1。
而同时，根据H的定义，如果已经知道了K，那么也可以反求出旋转矩阵R和平移t。因为H乘以K逆以后，得到的是r1、r2、t组成的矩阵，平移t就可以直接得到，而旋转矩阵已经得到了两个，根据正交性质，r3可由叉乘得到r3=r1×r2。需要注意的是数值求解得到的H中的r1、r2并不一定满足模长等于1的性质，因此还需要将其归一化。如上图所示可以使用第一列的模长a对三列都归一化，归一化后才对应旋转矩阵的第一列、第二列。
灭点计算相机姿态实例
在之前这篇笔记中基于OpenCV实现了相机标定，这里就用它的结果作为计算数据。标定得到的相机内参矩阵K如下：
\[\begin{pmatrix} 533.18 & 0 & 342.22\\ 0 & 533.18 & 235.01\\ 0 & 0 & 1 \end{pmatrix}\]如下是拍摄的棋盘格图片，图片大小是640×480。
标定板提供了水平和竖直两个方向的平行线灭点信息，首先测量出四个交点的像素坐标(为了计算方便写成了齐次形式)。先求四条直线的直线方程，取直线上的两个点做叉乘即可，如下：
求得四条直线之后，可以将两两直线做叉乘，进而得到两直线交点Vx、Vy。
\[\begin{matrix} v_{x}=l_{3}\times l_{4}=(16,287,-18729)\times (3,388,-175772)=(-43179712,2756165,5347)\\ v_{y}=l_{1}\times l_{2}=(-397,-52,75908)\times (-411,49,191719)=(-13688880,44914255,-40825) \end{matrix}\]注意还要除以z分量，使z=1才是像平面上的交点坐标。
\[\begin{matrix} v_{x}=(-43179712,2756165,5347)/5347=(-8075.5,515.5,1)\\ v_{y}=(-13688880,44914255,-40825)/-40825=(335.3,-1100.2,1) \end{matrix}\]然后根据公式：
\[\begin{matrix} r_{1}=K^{-1}z V_{x}\\ r_{2}=K^{-1}z V_{y} \end{matrix}\]这里由于最终是要对r1、r2归一化的，所以z有没有都无所谓，可以直接忽略，这样就可以得到初步的r1、r2：
\[\begin{matrix} r_{1}=(-84417,2812,5347)\\ r_{2}=(530,102230,-40830) \end{matrix}\]再对它们归一化有：
\[\begin{matrix} r_{1}=(-0.9974,0.0332,0.0632)\\ r_{2}=(0.0048,0.9287,-0.3709) \end{matrix}\]最后一步，对r1、r2做叉乘，即可得到r3。这里并不需要再对r3归一化了，因为前面说过两个正交单位向量的叉乘结果还是单位向量。在上面我们已经对r1、r2归一化了，所以它们叉乘的结果页自然是单位向量。如果不相信的话可以算一下得到的r3的模。
\[r_{3}=r_{1}\times r_{2}=(-0.0710,-0.3696,-0.9265)\]所以最后根据灭点求出的相机相对于标定板平面的旋转矩阵如下：
\[R = \begin{pmatrix} r_{1} & r_{2} & r_{3} \end{pmatrix}=\begin{pmatrix} -0.9974 & 0.0048 & -0.0710\\ 0.0332 & 0.9287 & -0.3696\\ 0.0632 & -0.3709 & -0.9265 \end{pmatrix}\]当然还可以继续根据上面的公式从r3求出pan和tilt角度：
\[\begin{matrix} \alpha = tan^{-1}(r_{3}(1)/r_{3}(3))=0.0765\\ \beta = sin^{-1}r_{3}(2)=-0.3786 \end{matrix}\]转换成角度分别是4.3821度(pan)和-21.6911度(tilt)，将这个角度与图片进行对比发现也是基本吻合的。相机相对于标定板在水平方向基本没有什么旋转角度，但在竖直方向有较大的旋转角度。
变换顺序与坐标
上面估计出了相机的旋转与平移，它在实际坐标系的意义如下。
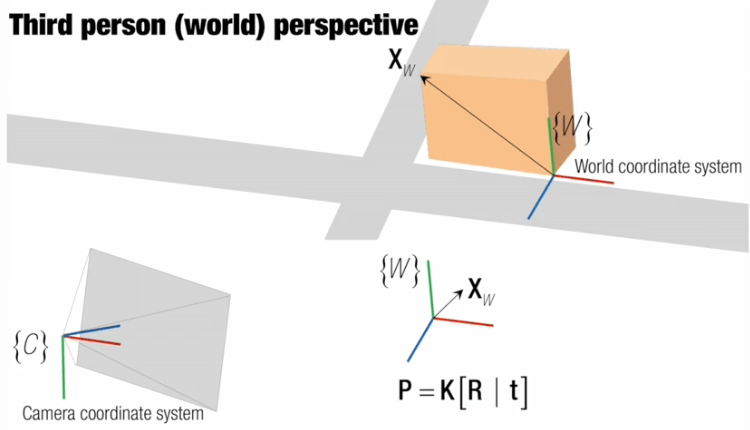
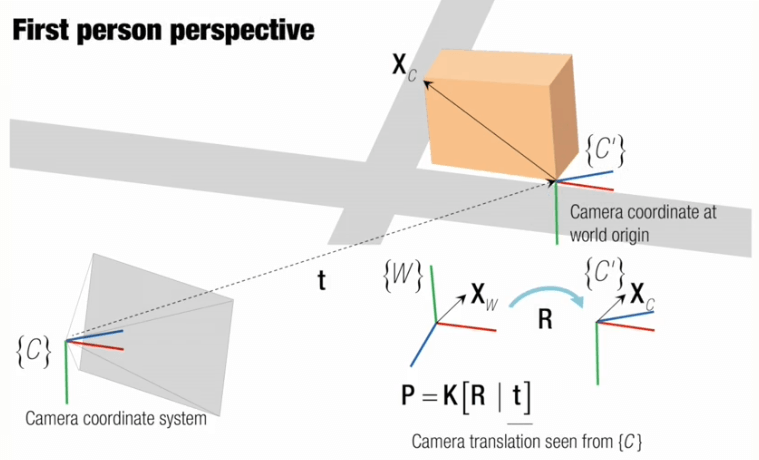在这里t表示一个在相机坐标系下的从相机坐标系原点指向世界坐标系原点的向量。
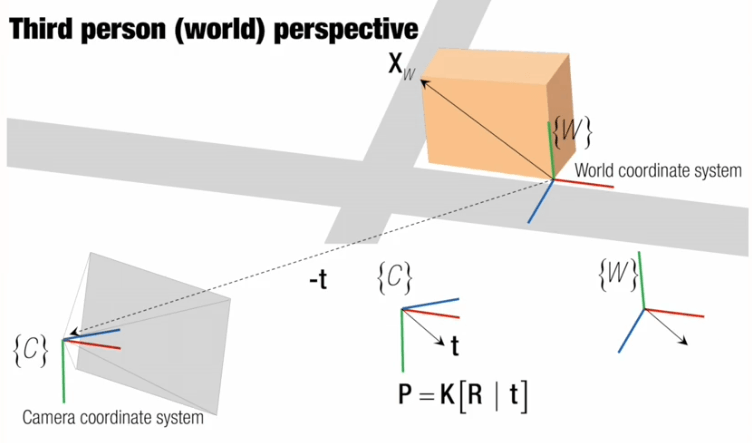而从世界坐标系来看，-t表示一个从世界坐标系原点指向相机坐标系原点的向量，方向与t相反。
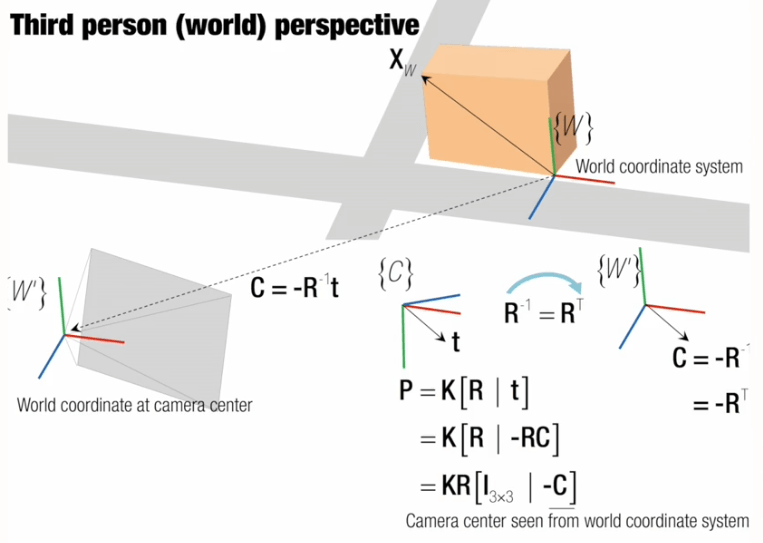然后通过旋转矩阵将在相机坐标系下度量的t转换到世界坐标系的度量下。
2.Compute Projective Transformations
投影变换的定义与性质
一个平面的透视投影(如相机拍摄的相片)本质上就是一个投影变换，投影变换定义如下：
对于两个投影平面，任何一个3×3的可逆矩阵变换都是投影变换。投影变换又被称作Collineation(共线)或者Homography(单应)。
投影变换的重要性质有：保留incidence、保共线(preservation of collinearity)、保平行(preservation of concurrency)。
直线在投影变换下的变换。设p’等于Ap，带回直线方程即可得到第二个式子，那么按照第一个式子直线方程的形式对应，就可以得到l’。这里l为直线方程的系数构成的向量，p为直线上的某点。
投影变换矩阵的计算
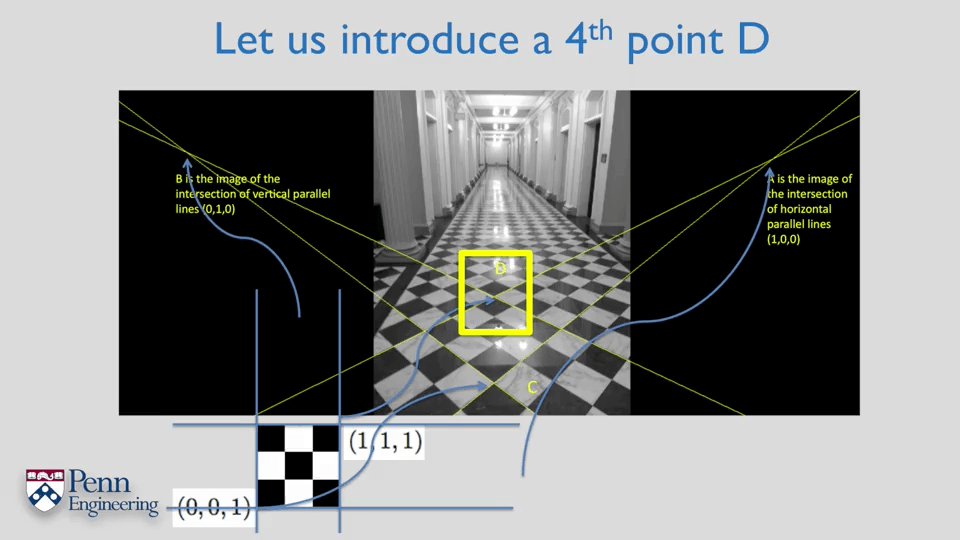至少需要4个对应点即可计算投影变换。简单来说就是利用三个非共线的点确定变换矩阵的“样子”(哪些元素非0，哪些元素是0)，再用最后一个点确定非零元素的值。
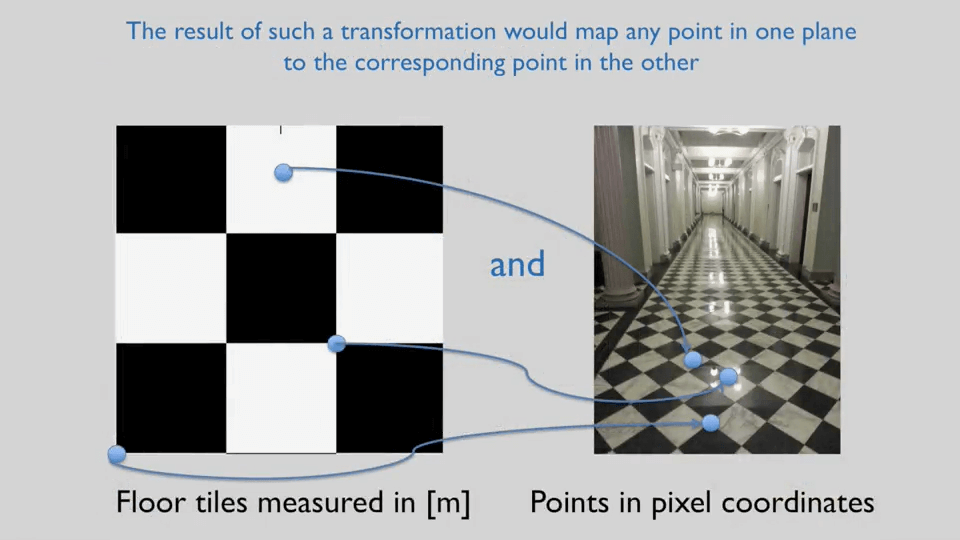
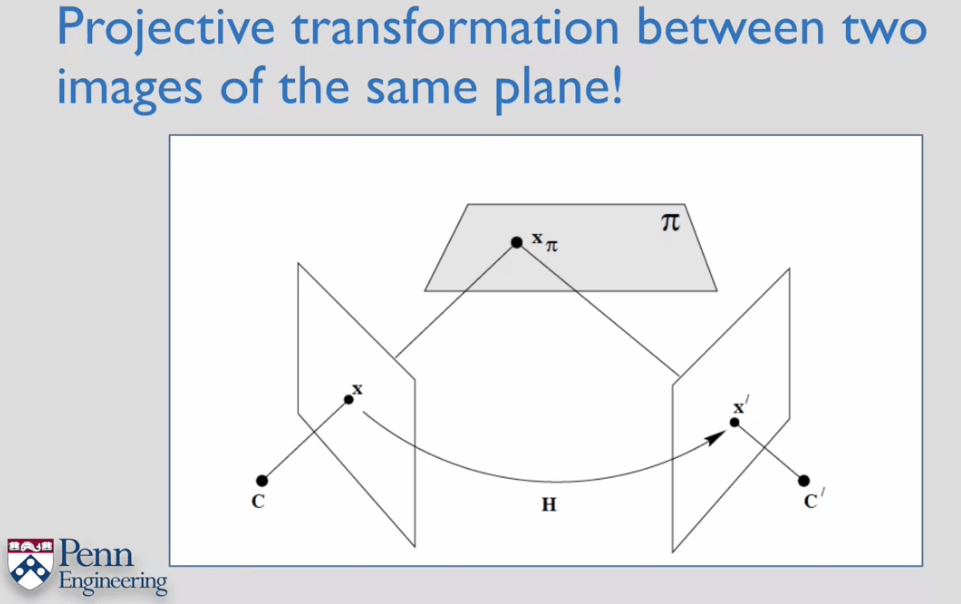
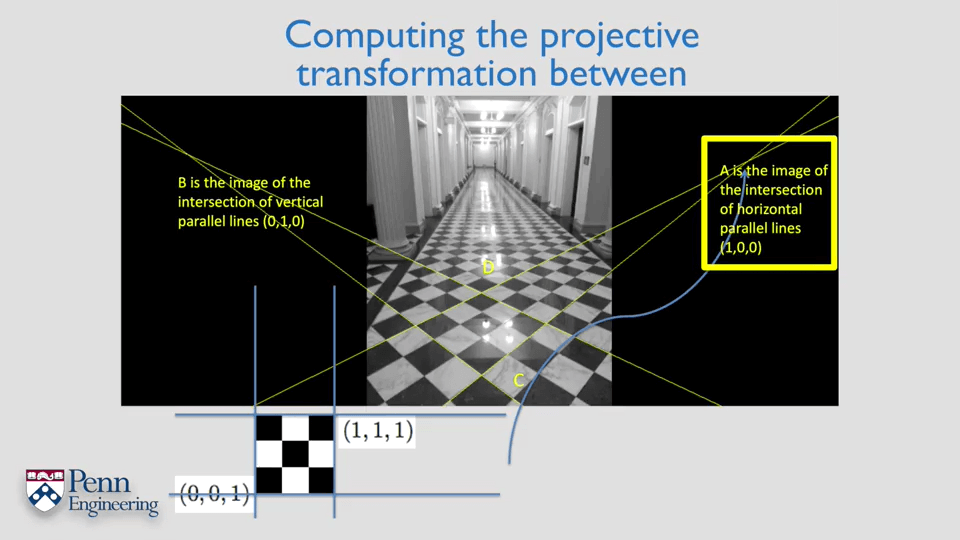对于两张影像上不知道真实坐标，只知道像素坐标的情况，如何计算两张影像间的投影变换呢？
简单来说就是构建虚拟坐标点，先求出虚拟点到第一张影像的投影变换，再求出虚拟点到第二张影像的投影变换，最后对两个运动代数方法合并两个变换，如下图中的第三个式子，即可得到两张影像间的变换了。
3.Projective Transformations and Vanishing Points
一个例子：
4.Cross Ratios and Single View Metrology
在平行投影中线段中点会保留，但在透视投影中则不会保留。那么对于一个投影变换而言，保持不变的是Cross-Ratio，交比。交比由一条直线上的四个点来定义。
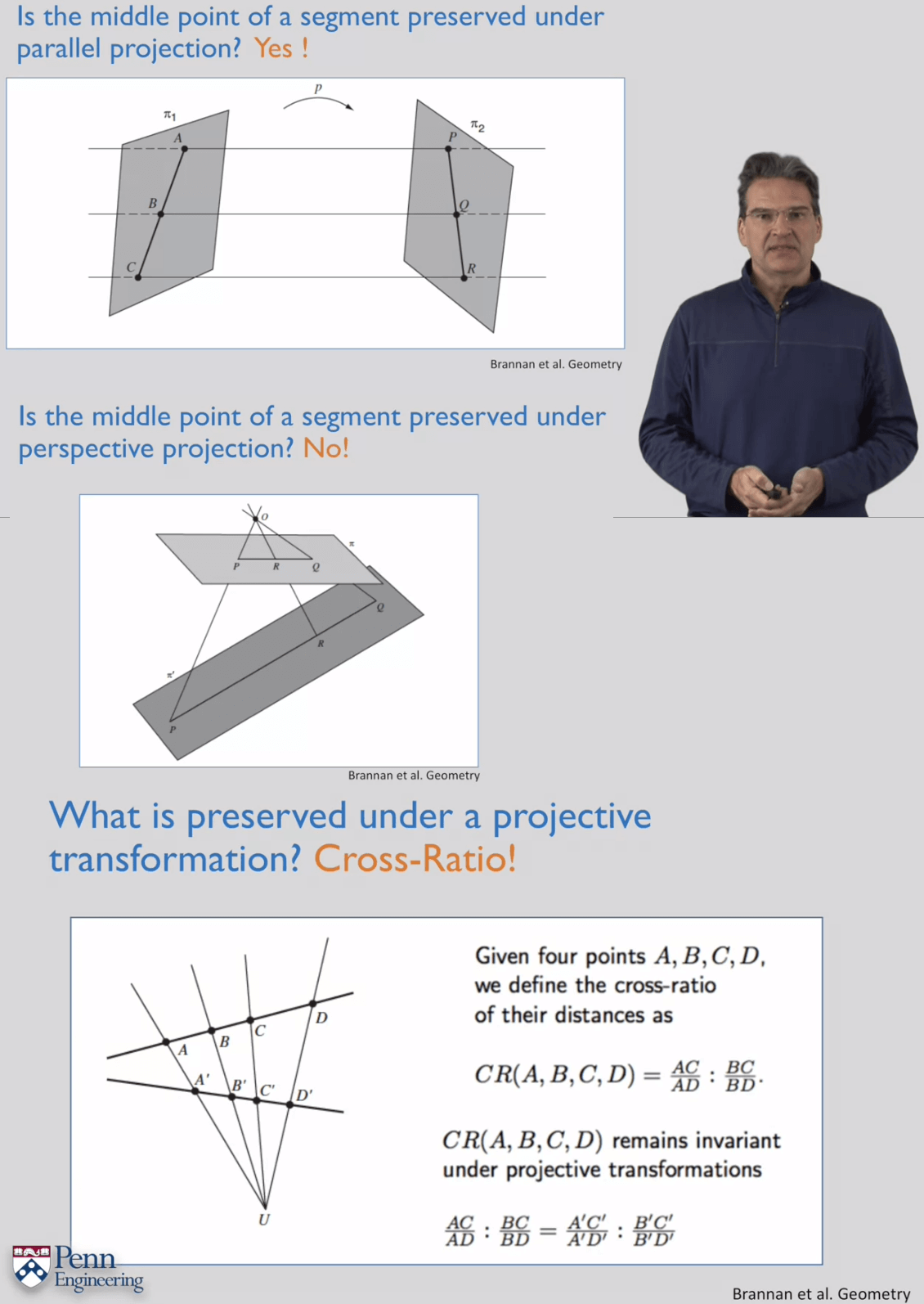交比的作用之一是可以用来对图片中的一些线段进行测量。
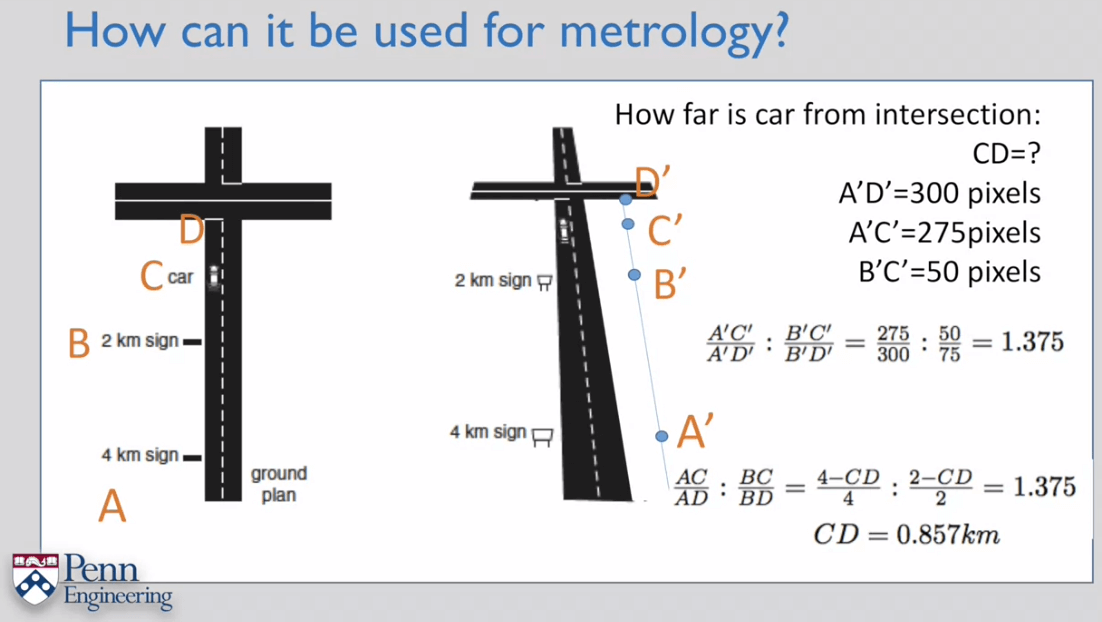而当交比的某个点位于无穷远处时，交比可以简化：
此时，利用交比同样可以进行测量，如下面这个例子：
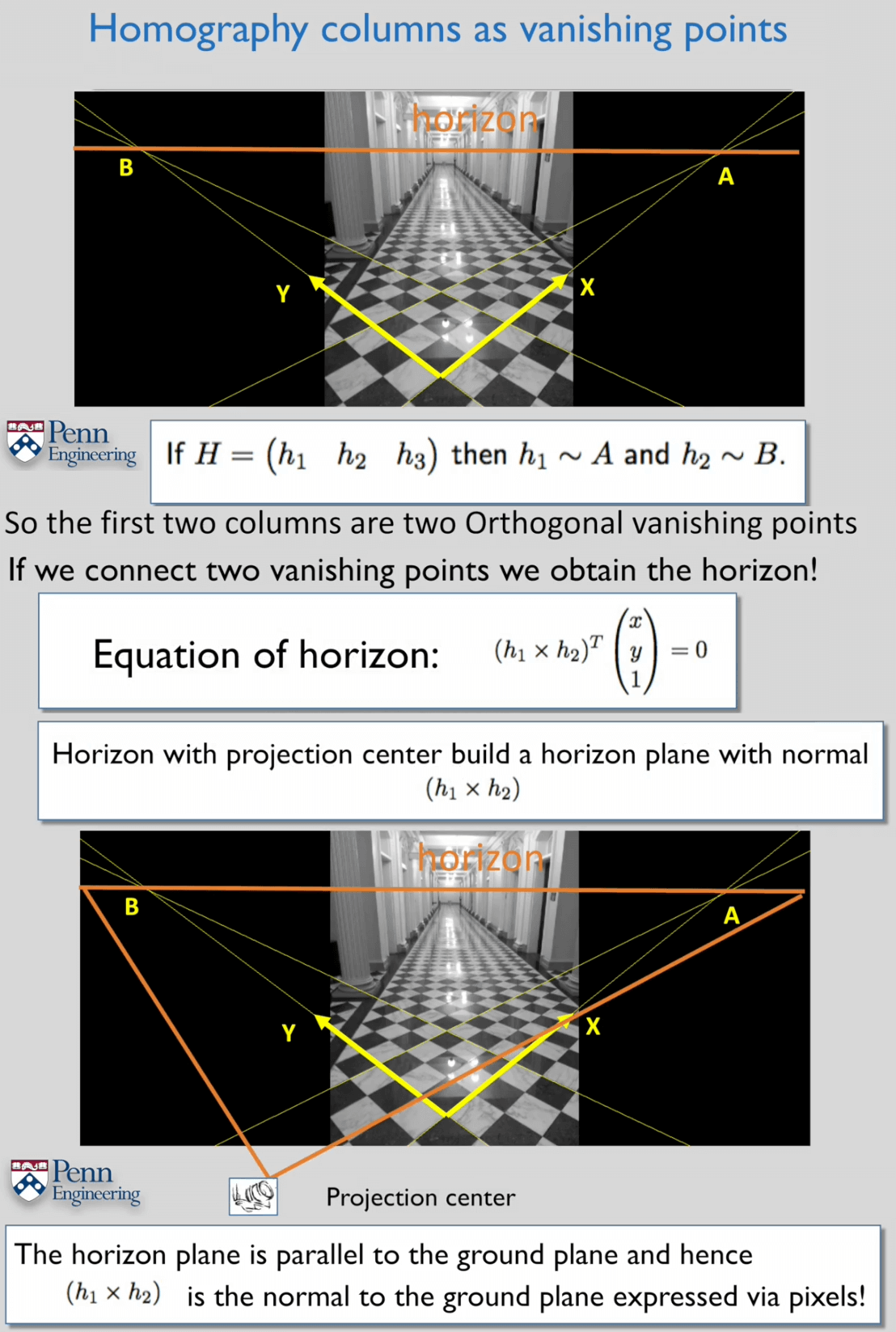
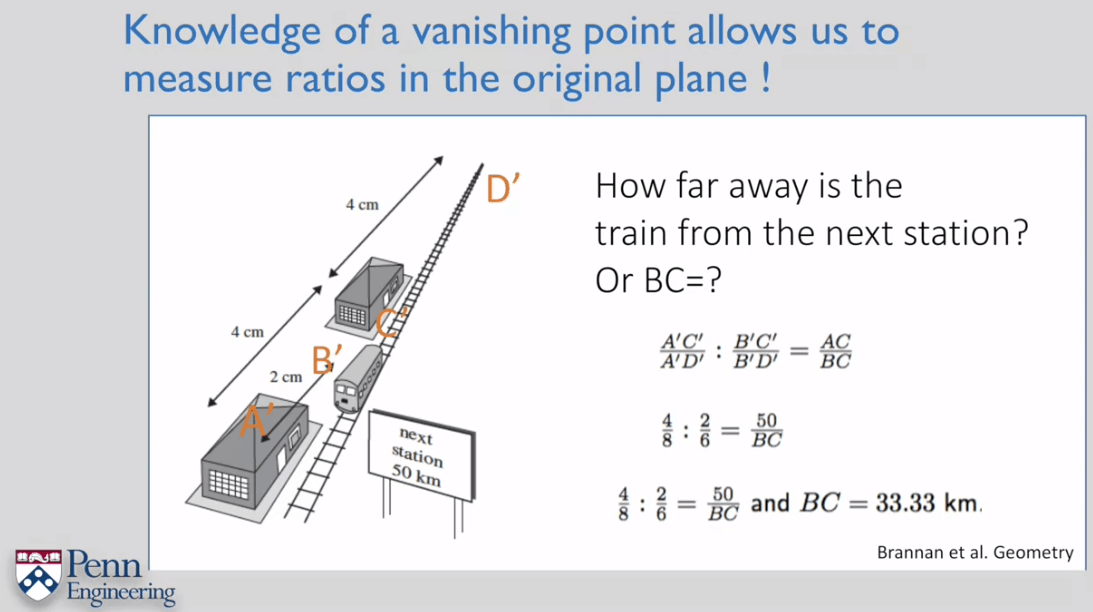换句话说，如果我们已经知道了两个方向上的交比，那么我们就可以根据交比推算出两个灭点，连接灭点即可得到地平线。
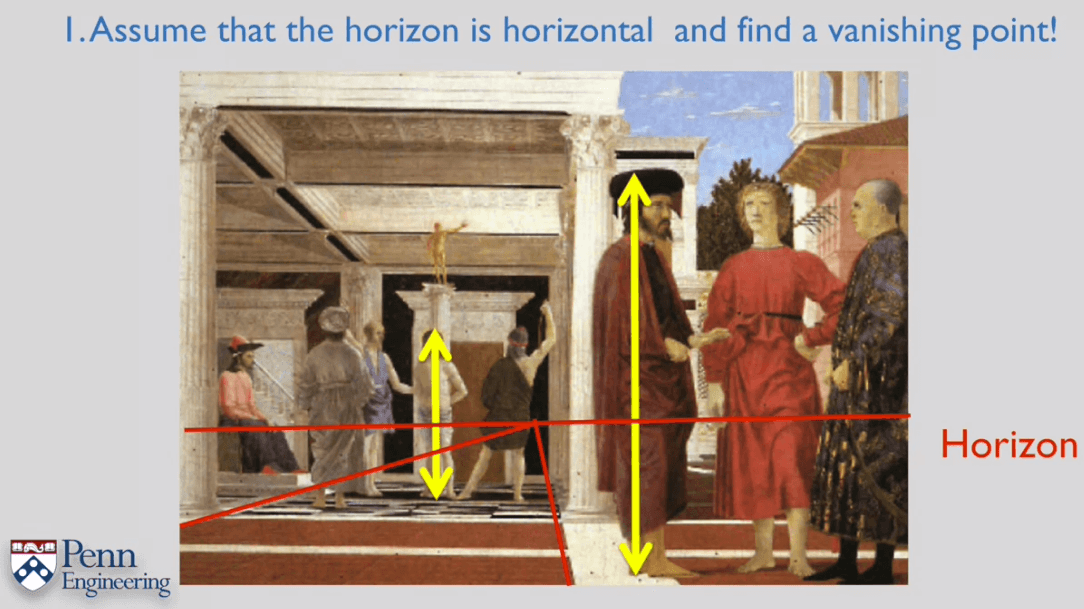
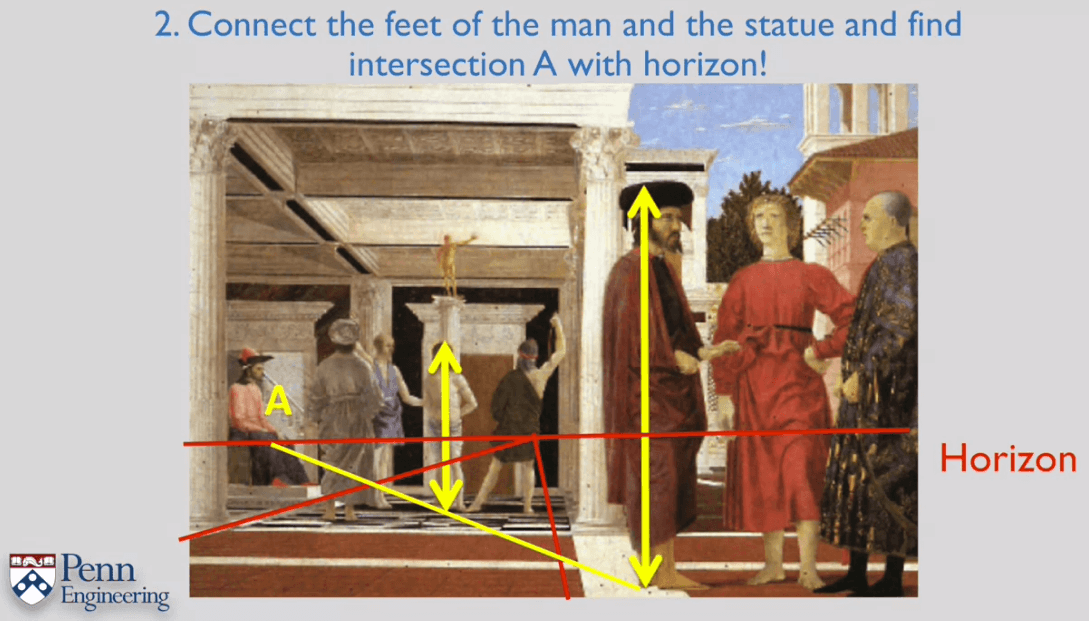
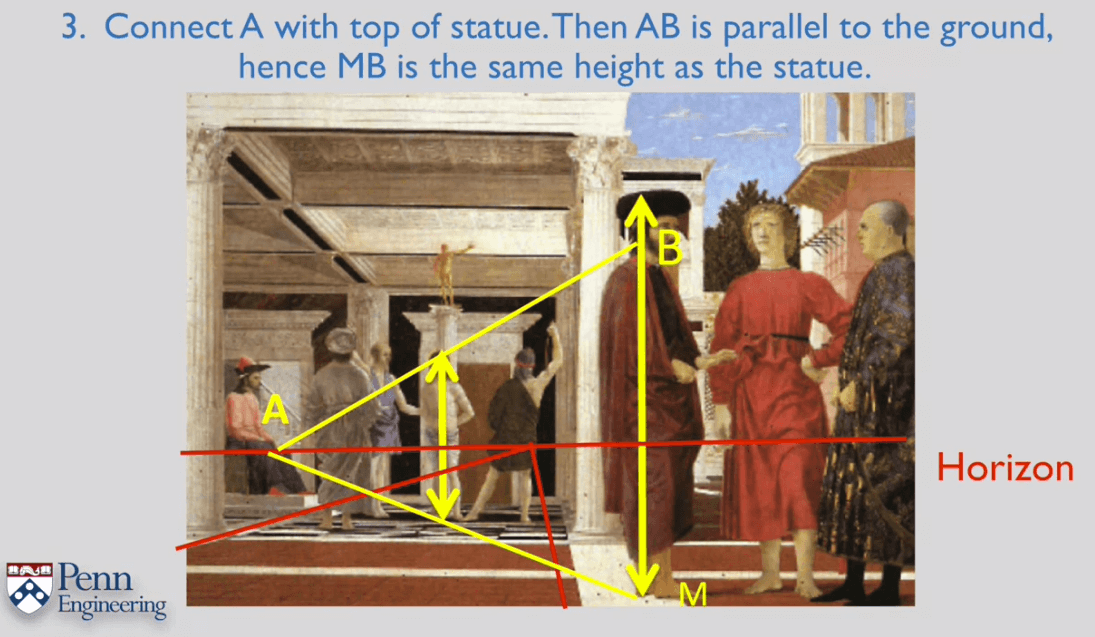
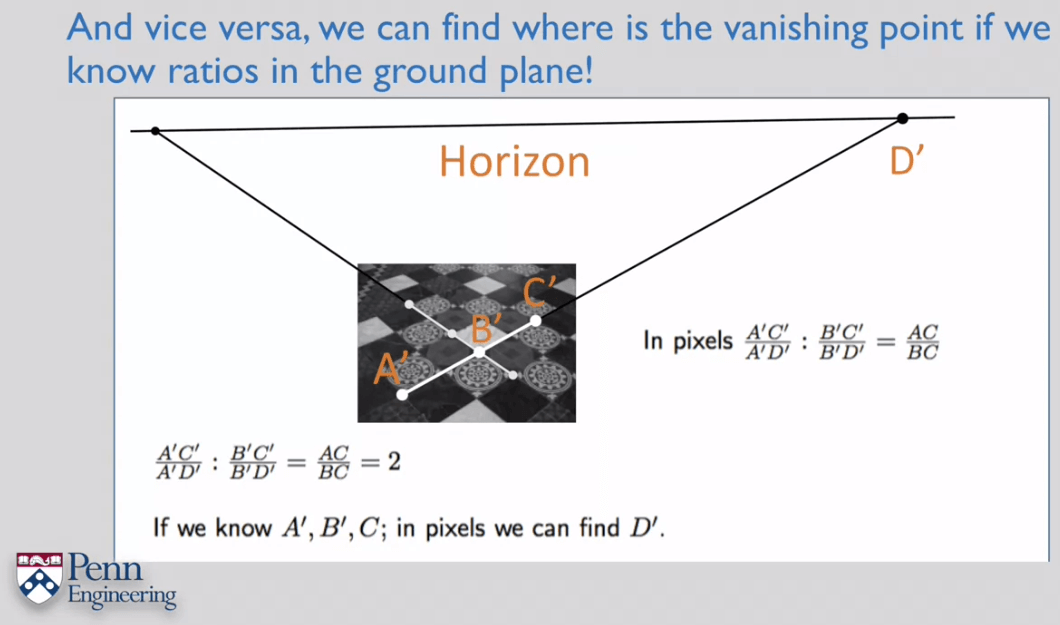一个利用交比计算高度的例子。
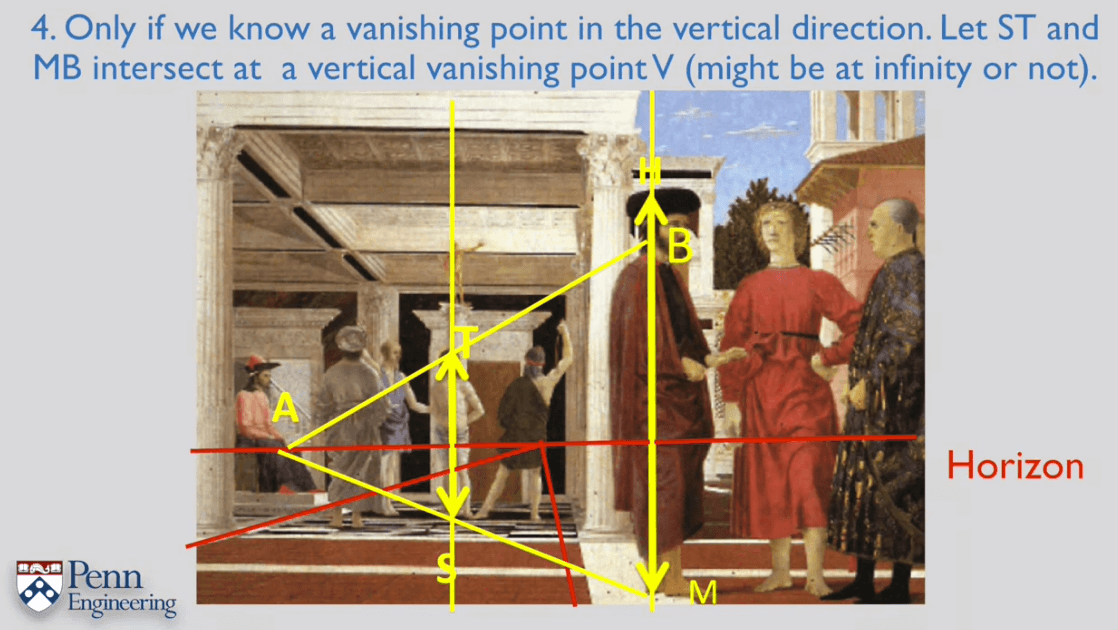
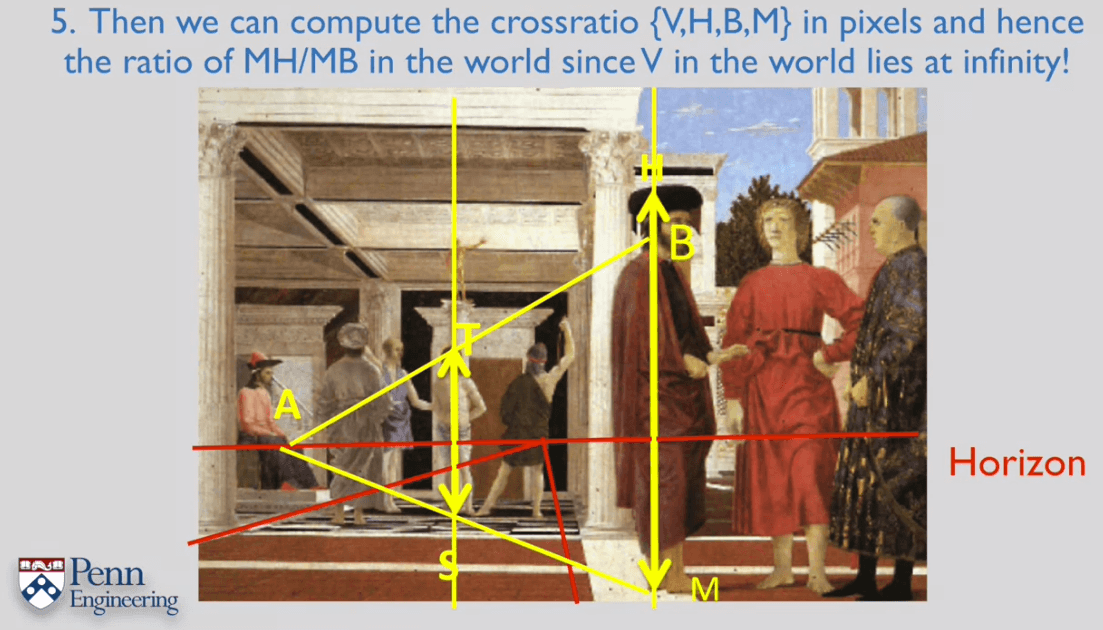
5.Two View Metrology
本文作者原创,未经许可不得转载,谢谢配合
