在之前这篇博客中说到了SVD,但当时只是介绍了其公式和应用,并没有从原理上学习。本篇博客从原理上对SVD进行相关分析。 因为在SLAM中会经常用到各种SVD分解,因此掌握SVD的原理对于深入理解SLAM中的相关算法还是很有必要的。
一、线性变换与矩阵乘法
在数学中,线性映射(也叫做线性变换或线性算子)是在两个向量空间之间的函数,它保持向量加法和标量乘法的运算。术语“线性变换”特别常用,尤其是对从向量空间到自身的线性映射。 线性变换在这种加法和乘法里所带来的拉伸效果或者说是解释向量如何在不同矩阵空间中表示。 假设有一个对角矩阵M,M乘以一个向量(x,y)可以看做M将点(x,y)变换为另一个点
\[\begin{pmatrix} 3 & 0\\ 0 & 1 \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix}=\begin{pmatrix} 3x\\ y \end{pmatrix}\]变换的效果如下,变换后的平面仅仅是沿 X 水平方面进行了拉伸3倍,垂直方向是并没有发生变化。
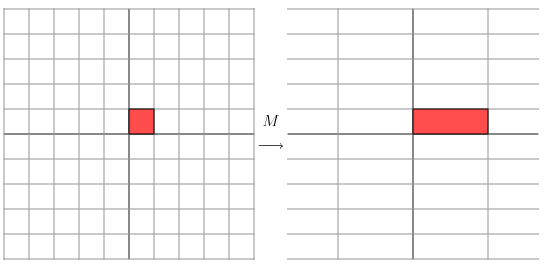
再看另一个矩阵
\[\begin{pmatrix} 2 & 1\\ 1 & 2 \end{pmatrix}\]用它乘以其它向量,产生的效果
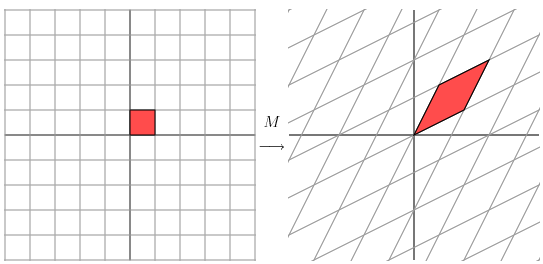
理解上面的变换,首先要有的一个概念是,一个矩阵的列向量就是一组“基底”(先不谈奇异矩阵)。这些基底就张成了一个空间。如果矩阵真的是奇异的,可以理解为这些基底重合了,形成了一条直线。如3阶单位矩阵I,它的列向量就张成了我们熟知的三维坐标系笛卡尔空间。
假设在三维空间中有一组标准正交基底x,y,z(都是列向量)。一个列向量V=(3,4,5)T,以及由x,y,z组成的矩阵A如下
\[A=\begin{pmatrix} x & y & z \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}\]向量V表示的是在X方向投影是3个单位长度,Y方向是4个,Z方向是5个。那么如果将矩阵A和向量V相乘,结果如下
\[AV=\begin{pmatrix} x & y & z \end{pmatrix}\begin{pmatrix} 3\\ 4\\ 5 \end{pmatrix}=3x+4y+5z\]A的列向量是标准基,描绘的是笛卡尔空间。向量V只是一个计量每个轴上有几个单位长度的东西。在笛卡尔空间中,X方向上的1个单位长度可以用矩阵乘法算得表示如下
\[IV = \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix}=\begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix}=x\]这里V的含义是表示X轴上取一个单位长度,其它轴为0个单位。因此我们可以利用这个来计算由不同基底形成的空间中的X方向的单位长度。如下面这个矩阵A形成的空间,利用这个办法便可以求得它X轴方向的单位长度。
\[A=\begin{pmatrix} 1 & 1 & 1\\ 1 & 2 & 2\\ 1 & 2 & 3 \end{pmatrix}\] \[\begin{pmatrix} 1 & 1 & 1\\ 1 & 2 & 2\\ 1 & 2 & 3 \end{pmatrix}\begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix}=\begin{pmatrix} 1\\ 1\\ 1 \end{pmatrix}\]可以看到,新的空间中的X方向单位长度变成了(1,1,1)T。这和之前在标准笛卡尔坐标系中的X方向单位长度(1,0,0)T是不同的。
再回头看一下之前那个2,1,1,2矩阵的变换。变换之前是标准的二维空间,两个基底相乘是等于0的,说明是正交的。而变换后的两个基底相乘为4,不再正交了。所以看到变换后的坐标系成了平行四边形。如果一个矩阵式正交矩阵,它和另一个向量相乘,新的空间以这些向量作为基底,说明在新的空间里各轴还是垂直的。这种拉伸便是旋转。所以可以理解为一个正交矩阵乘以一个向量,便代表着将这个向量旋转到了一个新的坐标系中。这就是SLAM中经常会看到的旋转矩阵R乘以一个p点坐标(x,y,z)表示对p点进行了旋转的原理。
而矩阵与矩阵相乘,同样可以理解为基底单位长度在不同空间中的表示。例如
\[C=A\cdot B\]不妨令
\[C=A\cdot B \cdot I=A \cdot W\]I为单位阵,它的列向量可以看成是笛卡尔空间的标准基底。W的列向量就表示I经过矩阵B变换以后的基底。而C的列向量就是W空间中的基底经过矩阵A变换后的新空间C的基底。
总结一下就是,一个矩阵可以理解为一个空间,它的列向量都是这个空间中的“基底”(这里所谓的基底不是严格意义上的基底,因为它们可能不是线性无关的,只是可以简单这样理解一下)。矩阵乘法就是在不同基底空间中转换表示,并且空间之间不一定都是同一大小纬度的空间。矩阵的秩可以理解为这个矩阵空间的体积,或者叫由标准空间向该矩阵空间转换时的体积变化因子。在线性代数中,一个矩阵A的列秩是A的线性独立的纵列的极大数目。类似地,行秩是A的线性无关的横行的极大数目。通俗一点说,如果把矩阵看成一个个行向量或者列向量,秩就是这些行向量或者列向量的秩,也就是极大无关组中所含向量的个数,一般记作rank(A)。最后再说一下一个容易和秩混淆的概念,矩阵的迹。在线性代数中,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)。注意区别。
二、特征值与特征向量
实对称矩阵属于不同特征值的特征向量一定正交(注意不是任意矩阵)。不同特征值的特征向量是线性无关的,也就是说不同特征值组成的特征向量组成了特征空间的一组基底。n阶方阵A若有n个线性无关的特征向量,那么A可以被对角化为A=P-1VP,P是特征向量矩阵。而对于特征向量与特征值的求法,在这个网页里有详细的介绍。
三、奇异值分解
对于一个m×n的复数矩阵M,可以写成
\[M=U\Sigma V^{*}\]其中U,V都是正交阵,\(V^{*}\)表示V的共轭转置,如果V是实数矩阵,表示转置。
例如,有一个M矩阵
\[M=\begin{pmatrix} 1 & 1\\ 0 & 1 \end{pmatrix}\]它所对应的拉伸可以图形化为如下
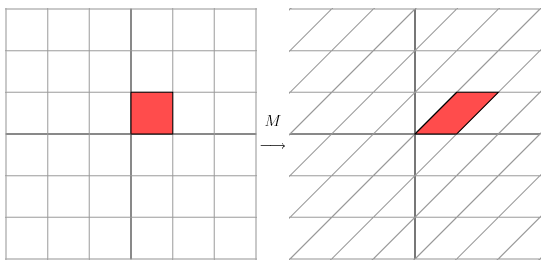
在左图中,基底是正交的,而经过M的拉伸后基底不再正交。那么有没有一种办法保留这种正交性呢?答案是旋转左图。
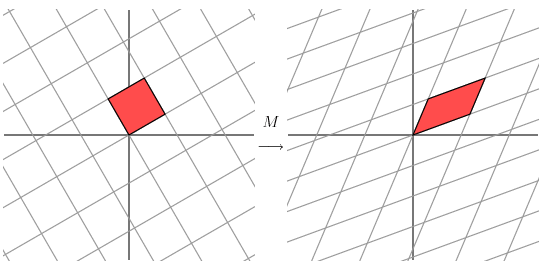
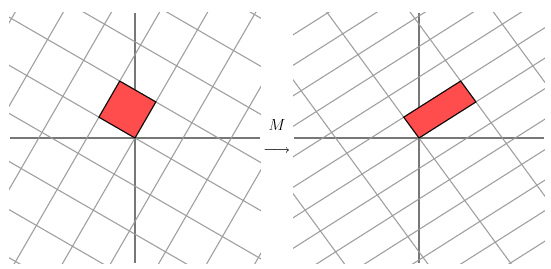
最终经过计算,转过58.28度后正交。
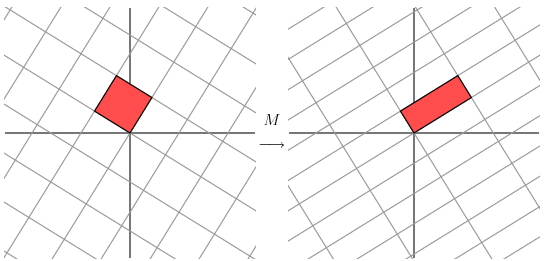
上面左图的这种旋转就是在标准基矩阵I的基础上做成一个单位正交阵(单位正交阵不改变原始基底的模长),从而使它变成VI,在VI的基础上再进行线性变换成M。
\[MVI=U\Sigma\]其中,V,U都是正交阵,U的列向量是变化后右图中的单位正交基。Σ可以看成是各个轴的伸缩量,学名奇异值。
将公式中的单位矩阵I去掉,假设V为实数矩阵,在等式两边右乘V的转置(正交阵V的逆等于V的转置),便可以得到奇异值分解的公式:
\[M=U\Sigma V^{T}\]V的列向量就是\(M^{T}M\)的特征向量,U的列向量就是\(MM^{T}\)的特征向量。Σ的对角线元素(非零奇异值)就是\(M^{T}M\)或\(MM^{T}\)的非零特征值的均方根。
下面是关于SVD分解的另一个例子。M矩阵可以看成MI,它是对单位圆进行拉伸。这种拉伸等效于先用正交矩阵V进行旋转,再用Σ进行伸缩,再用U旋转。

四、SVD的应用
1.求伪逆
若矩阵M的奇异值分解为
\[M=U\Sigma V^{*}\]注意这里的星号表示共轭转置,当V为实数矩阵时,共轭转置等于转置。那么M的伪逆为
\[M^{+}=V\Sigma^{+} U^{*}\]\(\Sigma^{+}\)是Σ的伪逆,是将Σ主对角线上每个非零元素都求倒数之后再转置得到的。求伪逆通常可以用来求解最小二乘法问题。
2.近似矩阵
奇异值分解在统计中的主要应用为主成分分析(PCA)。数据集的特征值(在SVD中用奇异值表征)按照重要性排列,降维的过程就是舍弃不重要的特征向量的过程,而剩下的特征向量张成空间为降维后的空间。这在之前的那篇博客中便说到了。
3.解方程
对于线性方程组Ax=b,求其最小二乘解。
如果A的秩是n, 则其唯一解是\(A^{+}b\); 如果秩小于n, 则有无穷多解, 其中的最小范数解仍然是\(A^{+}b\)。我们通常关心的也就是这个解。也就是对系数矩阵利用SVD分解求伪逆。
对于齐次线性方程组Ax=0。当A行数大于列数时,也即方程数大于未知数个数时,需要求解最小二乘解。在x的一范数等于1的约束下,其最小二乘解为矩阵\(A^{T}A\)最小特征值所对应的特征向量。求解方法有两种(matlab):
-
[V D] = eig(A'A);D为A’A的特征值对角矩阵,V为对应的特征向量。找到最小特征值对应的V中的特征向量即为最小二乘解。 -
使用SVD分解矩阵A,
[U S V] = svd(A);U由AA’的特征向量组成,V由A’A的特征向量组成。A’在Matlab中表示A的转置.因此,奇异值矩阵S中最小的奇异值对应的V中的奇异向量即为最小二乘解。又由于S中的奇异值一般都是从大到小排列的,因此一般V的最右一列对应的数字就是方程的解。
而对于超定的非齐次方程Ax=b; 当A的行数大于列数时,方程组无解,需要求解最小二乘解。在matlab中使用一个左除命令就可以得到最小二乘意义下的解。matlab: A\b。
五、SVD在SLAM中的应用
在上面说了SVD的普通应用后,具体到SLAM中,主要是用它来解方程和分解矩阵。例如在求得本质矩阵E后,对其进行SVD分解,得到U、Σ、V,然后根据公式计算出R、t。第二种应用是在求解本质矩阵E的过程中。由对极约束得到了很多方程,但这是一个方程个数远远大于未知数的方程组。需要用SVD分解来获得最小二乘解。
六、参考资料
- https://blog.csdn.net/heyijia0327/article/details/26757435
- https://blog.csdn.net/heyijia0327/article/details/26760737
- https://blog.csdn.net/heyijia0327/article/details/26762531
- https://blog.csdn.net/heyijia0327/article/details/26763903
- https://www.ams.org/publicoutreach/feature-column/fcarc-svd
- https://blog.stata.com/2011/03/03/understanding-matrices-intuitively-part-1/
- https://blog.csdn.net/adventure2008/article/details/40428843
本文作者原创,未经许可不得转载,谢谢配合
