Robotics:Perception课程笔记3 Part2

• 1.Where am I
  • (1)Vanishing Point Based Method
  • (2)Epipolar Geometry Based Method
  • (3)Homography Based Method
  • (4)PnP Based Method
• 2.Pose from 3D Point Correspondences or the Procrustes Problem
• 3.Pose from Projective Transformations
• 4.Pose from Point Correspondences or the Perspective N Point Problem（PnP)

1.Where am I

(1)Vanishing Point Based Method

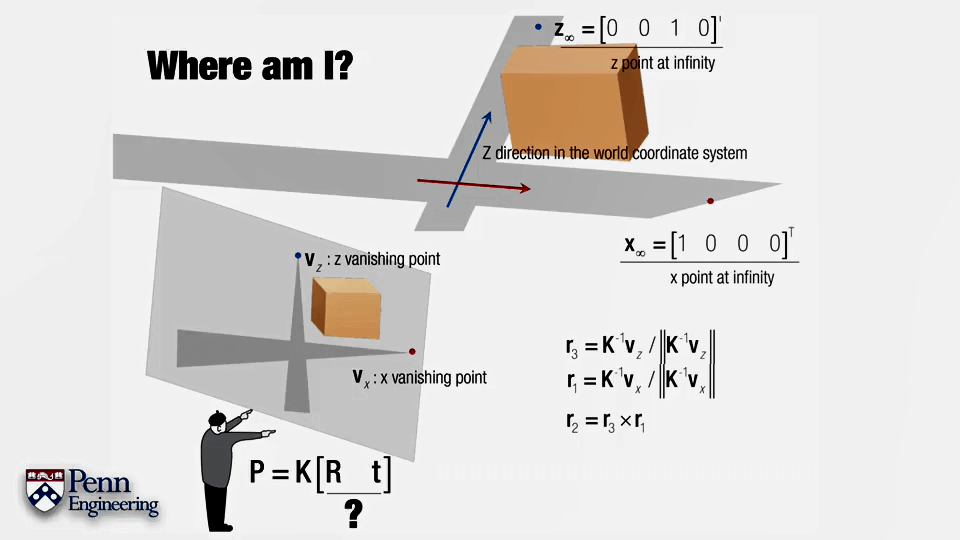在之前的课程中已经学习过了，通过影像中真实世界的两个垂直方向上的灭点即可以恢复相机相对于他们所在平面的姿态。

(2)Epipolar Geometry Based Method

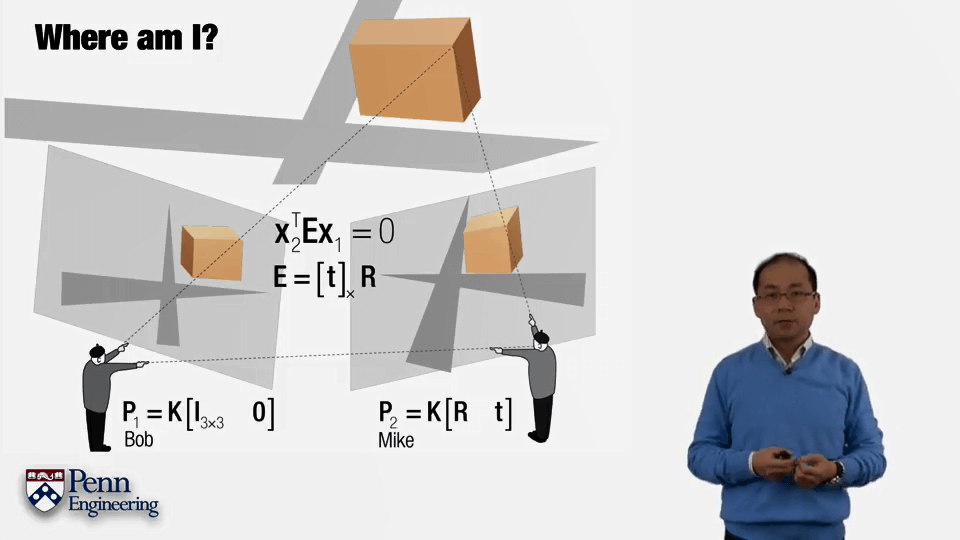除了在单张影像中使用灭点，还可以在两张影像间利用对极几何计算相机相对位姿。

(3)Homography Based Method

对于真实世界中位于某一平面上的物体，如果我们知道它们的一些物理属性(实际大小)，当我们使用相机拍摄它们时，就可以利用单应投影(Homographic Projection)来求得拍摄时相机相对于该物体所在平面的位姿。事实上，对于物体的实际大小，是很容易知道的。如标定板格网大小、人造物体：门、窗等。

需要说明的是，在一幅影像中可以存在多个平面，选择不同的平面进行单应矩阵求解，很显然最后求得的单应矩阵也是不同的。表示相机拍摄时刻相对于不同平面的位姿，如相对于墙壁、相对于地板等。这是十分灵活的，不要“死死地”认为两张影像间只能求一个单应变换。

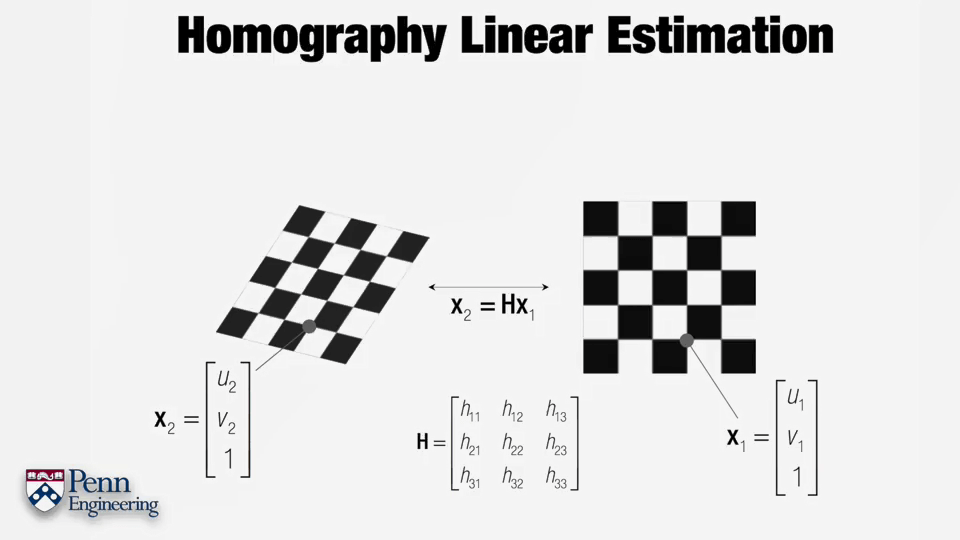如上图所示，右图为真实世界中的标定板的俯视图。在其中有一个已知点X1，假设它在标定板平面内的坐标为(u1,v1)，写成齐次形式，末尾加1，为(u1,v1,1)。某相机拍摄了它的照片，如左边所示，容易测得对应X2的像素坐标为(u2,v2)，写成齐次形式为(u2,v2,1)。这样我们可以通过一个3×3的单应矩阵H实现单应映射(Homography Mapping)。仔细观察H可以发现它联系的是真实世界的坐标与像素坐标，从物理意义上说也就是相机的内参矩阵K、外参(旋转R、平移t)都包含在了这9个元素中。因此只要能利用对应点对求解H，就可以求得相机相对位姿，这是一个核心问题。

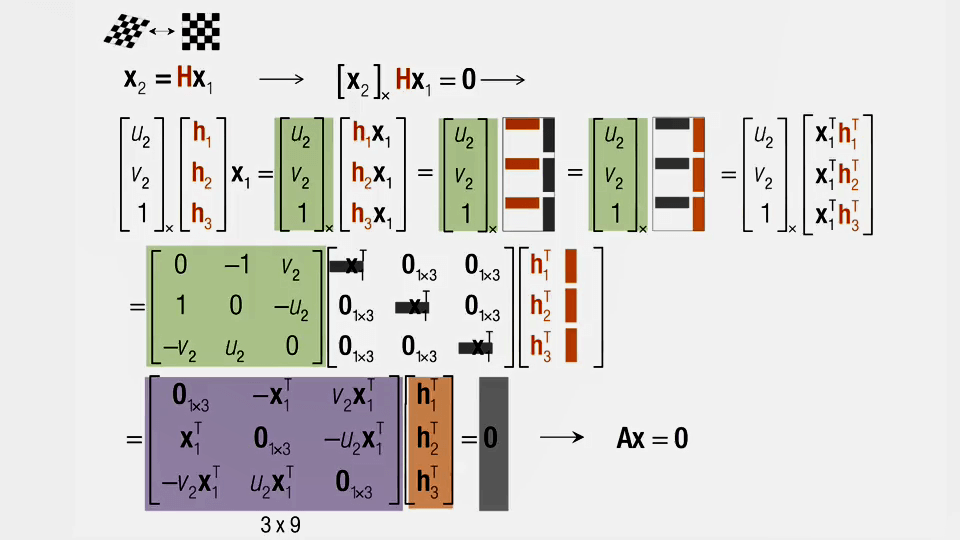求解单应矩阵的过程如上图所示。X1为齐次的真实世界坐标，X2为齐次的像素坐标，橙色的H为未知量。看到这个式子“本能的”反应是方程两边同乘以X1的逆不就得到H了吗？但仔细一看会发现这里X1是向量，还是3×1的，没办法求逆(非方阵没有逆矩阵，只能求伪逆)。所以直接乘以X1的逆的想法就不行了。所以这里使用了个小技巧：等式两边乘以X2的叉乘，左边X2与自身做叉乘结果为0向量，右边则是乘上X2的反对称矩阵(3×3)，它是一种固定格式的矩阵，之前在这篇博客里有介绍过。在后续式子中，为书写方便不妨将H矩阵按行拆分成h1、h2、h3，大小都是1×3。这样，根据矩阵乘法法则HX1其实可以写成h1、h2、h3分别与X1相乘，每一行得到一个标量，3行得到一个3×1的向量。写成这样以后可以使用第二个小技巧：根据矩阵转置法则(AB)^T=B^TA^T，对AB转置，结果不变，但AB的位置交换了。例如(1 2 3)与(4 5 6)^T相乘结果等于(4 5 6)乘(1 2 3)^T。我们希望未知量都在最右边(构造Ax=0的形式)，所以我们对HX1取转置，就可以得到X1^TH^T，实现了H与X1的位置互换。用h1、h2、h3表示就是图中第一行最右边的式子，这样我们就成功将H移到了最右边。但现在还有个问题，X1与H是“粘”在一起的，我们要想办法将它们分离。利用线代的知识，可以很容易把X1改写成一个“对角阵”(之所以加引号是因为它的形状并不是严格的对角阵，只是类似)，对角线元素即为X1^T，它的形状为3×9，这样便成功实现了“分离”。最后将它与前面X2的反对称矩阵相乘，即可得到3×9的系数矩阵A，如图中最下面一行的紫色部分所示。这样每一对点都可以写出上面这种形式的方程组，多对点如4对时候的A矩阵大小即为12×9。

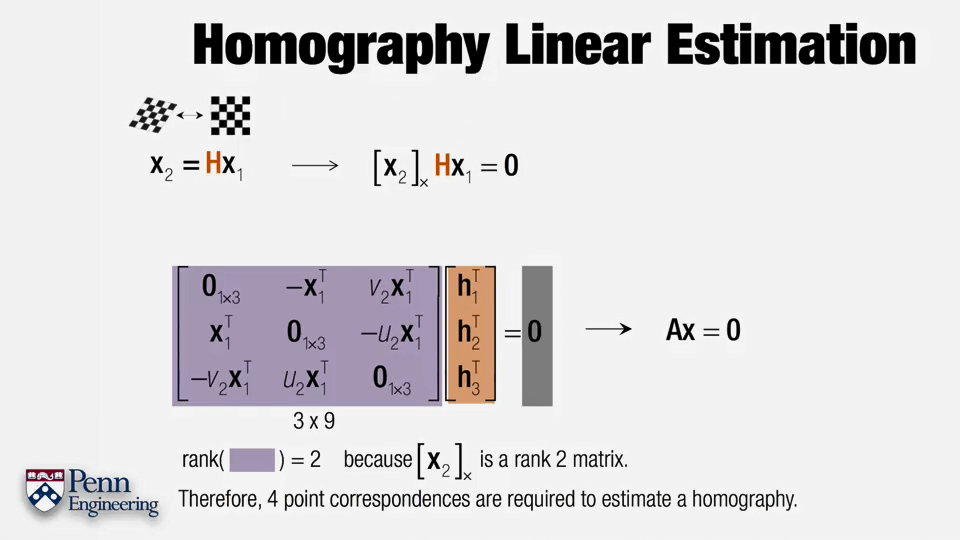在得到了方程后，可以对方程进行求解。A的秩为2，所以需要至少4对点才可以求解。而对于多于4对点的情况，在就可以用最小二乘方法解决了，具体办法是对A进行SVD分解，得到的V的最右边一列即为结果。这在上一篇笔记中说过了。

得到单应矩阵后可以根据H所包含的几何意义恢复出相机位姿。这部分内容在这篇笔记里也有提到。这里需要注意的是，正如前面提到的，H包含了相机内参矩阵K以及外参R、t，所以要想获得外参还需要先把内参去掉。不含内参的H应该在采用数值解法求得的H左边乘以K-1。这样得到H以后，H的第一列对应r1、第二列对应r2、第三列对应t。对r1按照H第一列列向量归一化，得到的就是R的第一列，r2等于H第二列除以第一列列向量模长，r3等于r1×r2，t等于H第三列除以H第一列列向量模长。根据公式可恢复出相机的旋转与平移。

这里一定要注意：并不是所有的单应矩阵都包含内参矩阵K。其实根据前面学习的定义，单应矩阵映射了三维空间中两个不同平面上的点的变换关系。是一个数学上纯理论的概念，与相机内参矩阵K毫无关系。例如在第二周的作业中求解单应矩阵时，给定两张影像中的4对对应像素坐标即可以求得平面区域的单应变换关系，直接构造Ah=0方程，SVD分解就得到结果了，与内参矩阵K无关。之所以在这里H包含了K是因为这里单应矩阵映射了像素坐标与真实世界坐标的关系，而将像素坐标转成三维坐标是需要内参矩阵K的，所以单应矩阵就把K给“吸收”了进来。这一点需要注意和理解。

(4)PnP Based Method

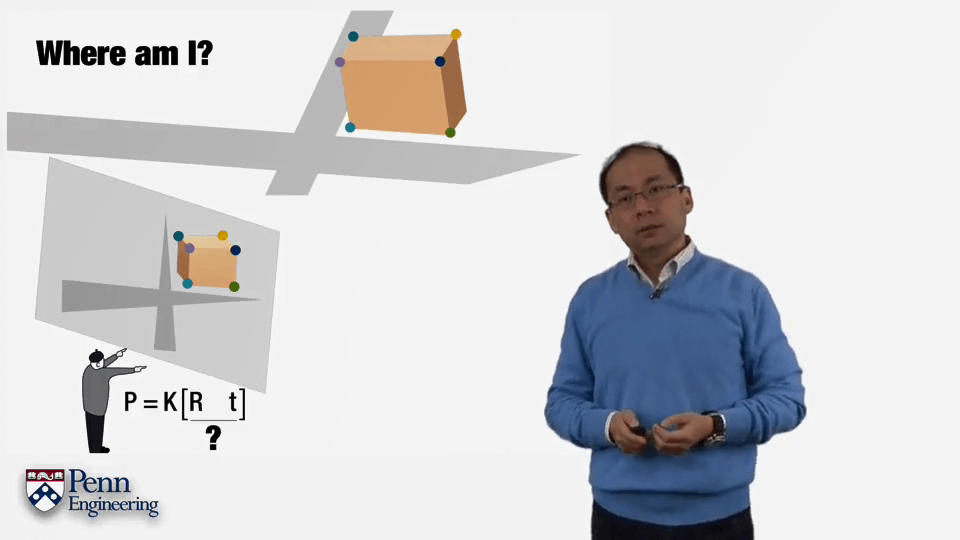而考虑一般情况，对于那些不是在同一平面上的点，如何估计相机位姿。

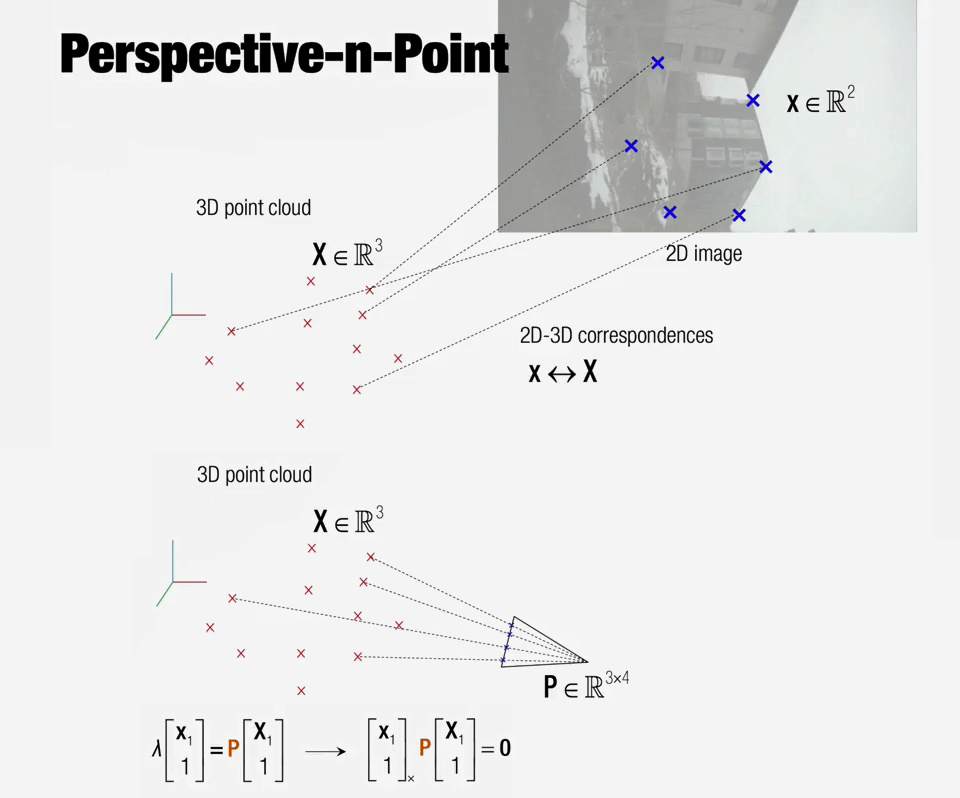PnP原理示意如上图所示。简单来说，我们通过人工匹配或算法找到了2D(Image Feature)-3D(Point Cloud)的匹配点对。二维特征点为x1，三维空间点位X1，将它们各自增加一维写成齐次。假设它们通过一个3×4的矩阵P(Projection Matrix)变换，λ表示从相机光心到真实三维点的距离。与单应矩阵H类似的，矩阵P中包含了内参K以及外参R、t，只要我们求得了P并且知道K，就可以恢复出R、t。这里采用与求解H类似的技巧，对齐次表示的x1向量(3×1)做叉乘，这样等式左边即为0，右边是其对应的反对称矩阵。通过一系列变换，使得未知量P在右边，已知量在左边作为参数，变成Ax=0形式。

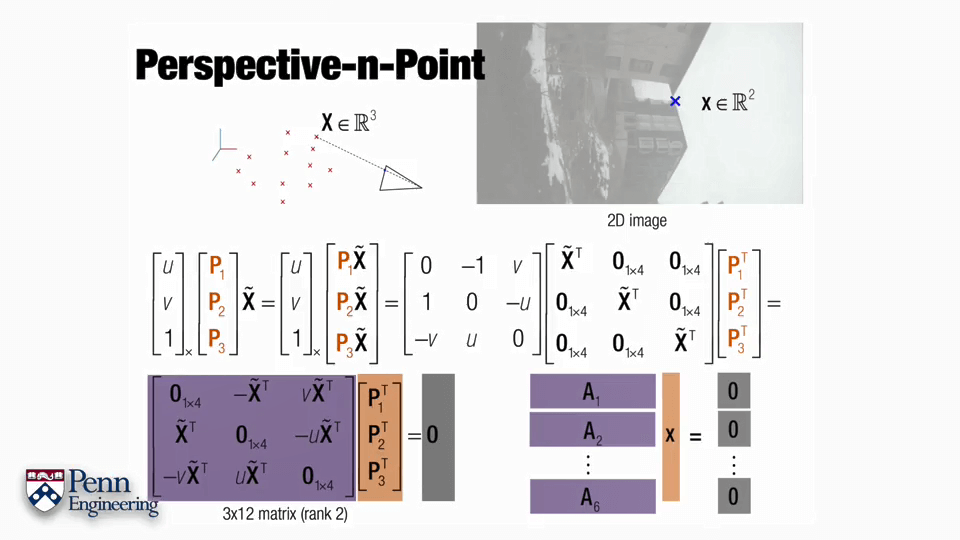PnP方程构建与求解。每对点提供2个独立的约束，P有12个元素，因此至少需要6对点(提供12个约束)才可以求解。在6对点时，稀疏矩阵大小为18×12。此方程可以使用最小二乘求解，对A进行SVD分解，数值解即是V的最右边一列。前4个元素为P的第一行，然后是P的第二行、第三行。

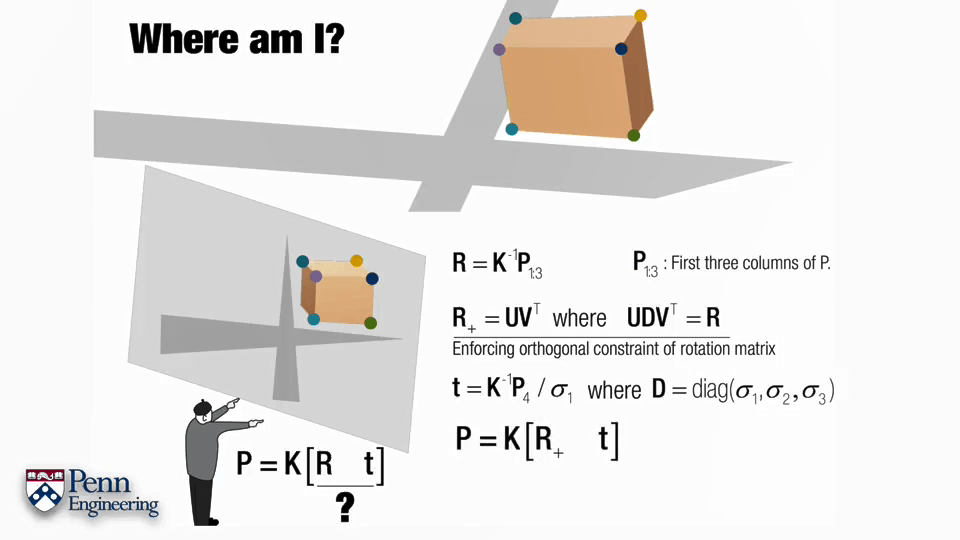根据求得的P分解得到R、t。与H类似的，将K-1左乘数值求解得到的P’即可得到不包含内参的P。P’的前三列并不是最终我们想要的旋转矩阵R，我们还需要对前三列进行SVD分解，将分解的U和VT相乘，得到的这个矩阵才是我们想要的旋转R，这样做的目的是矩阵满足正交性。对于平移t，我们将P’的第四列除以原始P’矩阵前三列SVD分解的最大奇异值，即可以得到真实平移量。

需要简单说明的是，其实对于PnP的2D-3D位姿估计，其中的3D点并不仅仅局限于是点云，而可以是其它任何已知的真实世界中的3D点，例如GPS测量得到的X、Y、Z都是可以的。

2.Pose from 3D Point Correspondences or the Procrustes Problem

简而言之就是给定一组对应的3D点对，找到它们之间的缩放、旋转以及平移关系。这种变换称为相似变换(similitude transformation)。在实际的刚体变换中，缩放s可以忽略，因此重点关注旋转与平移。这种3D-3D的变换可以用于如三维点云的对齐与配准。

因此问题就转化为了已知一些三维点对计算R、t。当然第一个问题就是我们需要最少多少个点就可以计算。我们不妨从四个点开始，A2-A1为向量A21，A3-A1为向量A31。那么让向量A21与向量A31做叉乘，就可以得到方向满足右手定则且垂直于A21、A31组成平面的向量，不妨叫做A’。而得到这个向量后，再将其与向量A21再做叉乘，即可得到图中虚线所示的向量，不妨叫做A_。这个虚线向量与A21和A’都垂直，而A’又垂直于A21，所以它们构成了一个三维基底(坐标系)。同理我们对B也可以得到这样一个基底。这样我们可以唯一地计算这两个坐标系之间的旋转。因此，只需要三对点即可以求解这个问题。

但问题是，对于大多数情况下，实际匹配的点对是远远大于三对点的。这种情况我们将这个问题转化为一个优化问题，寻找变换(R、t)使误差总和最小。而t其实是可以通过计算A和旋转后的B的质心的差异得到的，简单来说就是计算A中所有点的平均值与旋转后B中所有点的平均值的差异。因此就可以对上式进行简化，得到A-RB。A、B均为减去均值后的坐标。

采用矩阵论中的知识，形如这种的式子叫做Frobenius范数。式子中的前两项与R、t无关为常数，因此我们的优化目标就变成了最大化上式中的后两项。最终得到的R即为上图最后式子所示，平移t刚刚已经说了求解方法，A的质心与旋转后B的质心的差异。

3.Pose from Projective Transformations

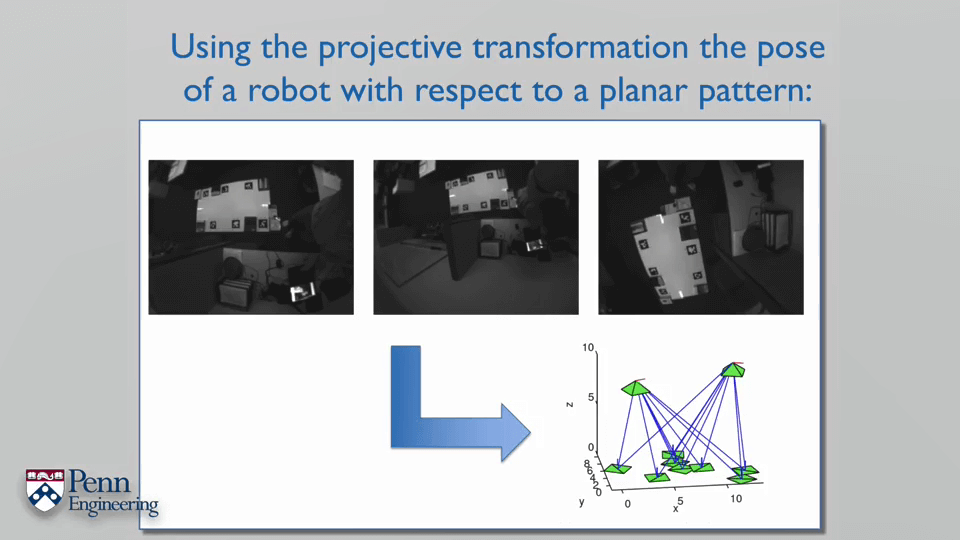
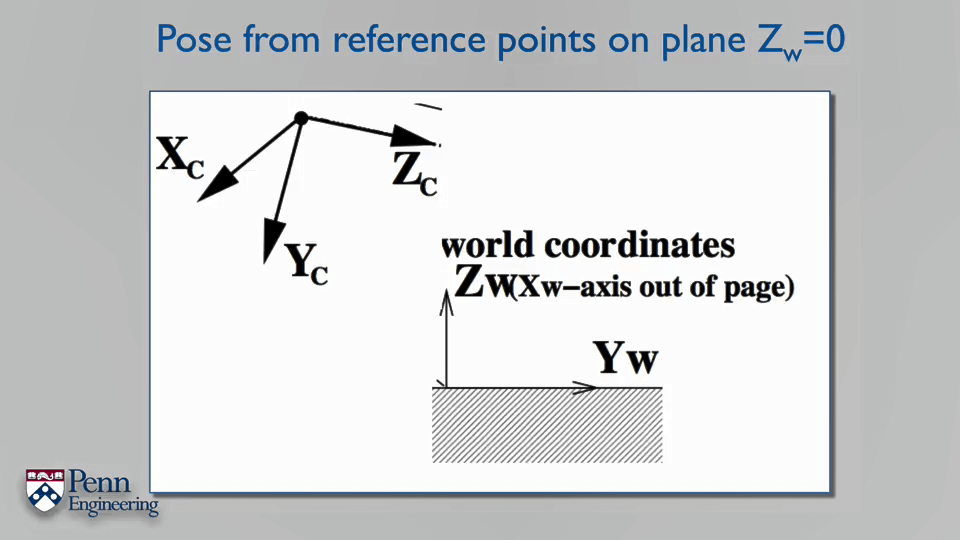利用投影变换也可以求解相机的位姿。

由于这些特征都在地面(Zw=0)上，所以我们可以认为这些点的真实坐标的Z分量都为0，这样根据矩阵乘法，变换关系就可以简化。而且如果对前面介绍的单应矩阵有印象的话，这其实就是单应矩阵H。还是再强调一下H中的r1、r2分别表示地面上的x、y轴在相机坐标系下的表达(或者换句话说是世界坐标系的x、y轴相对于相机坐标系的旋转)。

任何一个可逆变换都可以看作是一个投影变换。要看一个变换是不是可逆，可以检查变换矩阵对应的行列式的值是否为0。对于这里的情况，内参矩阵K的行列式值为f平方，因此当H的行列式不为0时，可逆。

因此我们可以使用单应矩阵H来估计相机的位姿。

4.Pose from Point Correspondences or the Perspective N Point Problem（PnP)

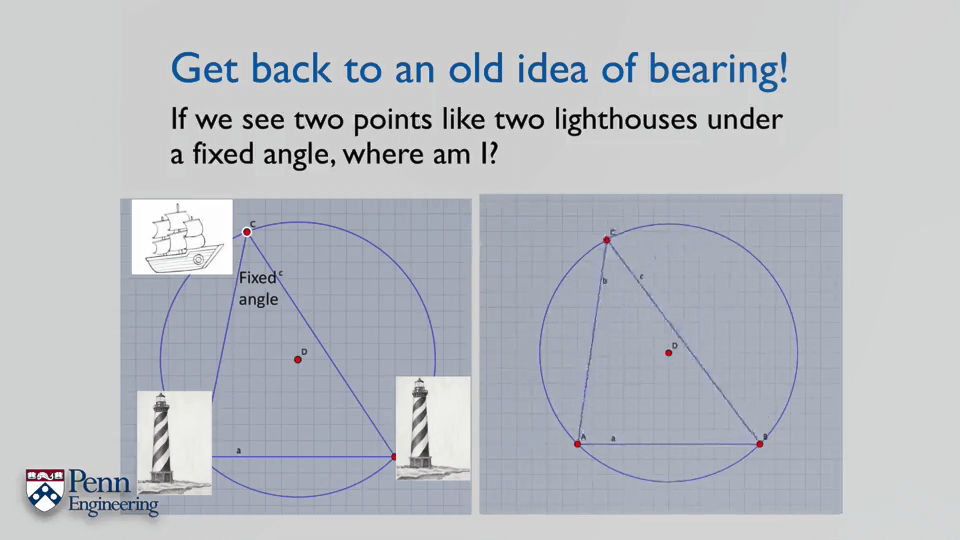
如上图所示，如果利用罗盘等测得了船相对于两座灯塔之间的夹角，如何估计船所在的位置。可以发现，此时是无法精确确定船的位置的，船在圆上的任意一点运动夹角都相同。而对于3D情况，不确定会变成一个曲面。

因此我们需要第三个点来帮助定位。这在摄影测量中被称作后方交会。在计算机视觉中，这又被称作P3P问题(Perspective 3-point Problem)。

P3P可以利用余弦定理求解。

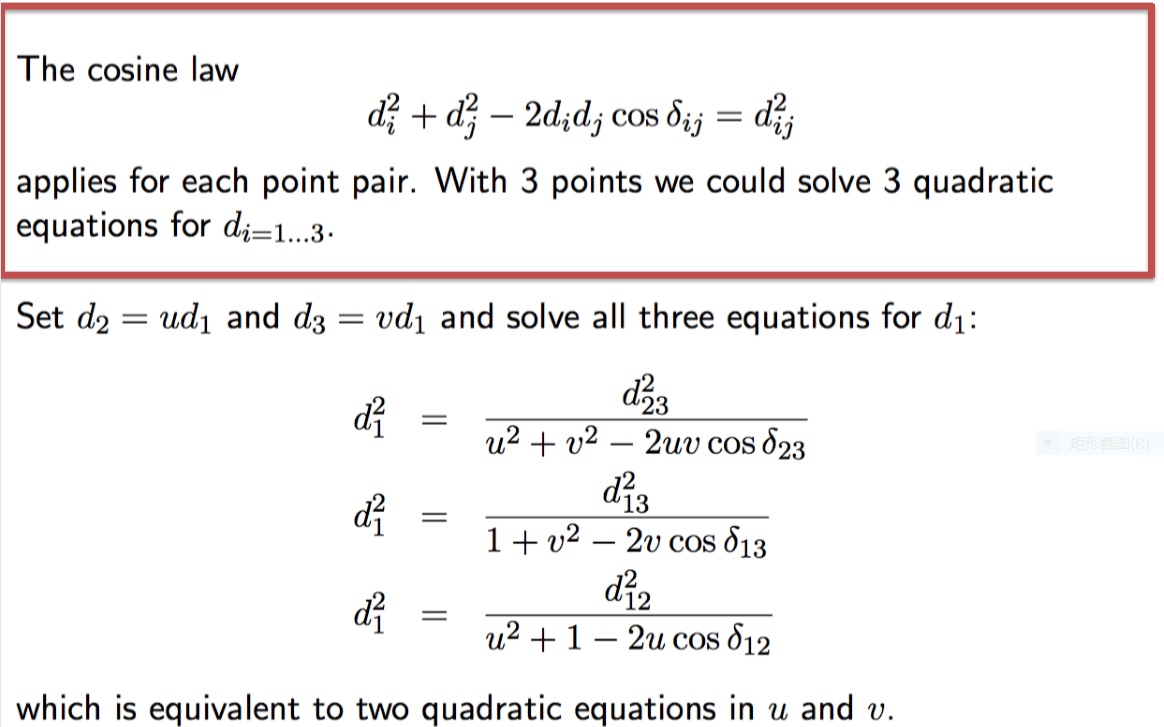
PnP还可以用直接解法求解。 将上面矩阵形式的式子“简单粗暴”地拆解后可以得到它们相互之间的表达式，由于刚体变换的未知数是6，所以至少需要3对点进行求解。这其实就是摄影测量里说的共线方程。这是一个非线性方程，因此需要迭代求解。 对于这个式子一个比较“脏”的办法就是去解一个包含12个未知量(旋转+平移)的方程，然后利用SVD分解，找到最贴近的答案。